Fizikai Szemle 2001/2. 37.o.

AKI AJTÓT NYITOTT A KVANTUMOK VILÁGÁRA

Max Planck és a százéves kvantumhipotézis

Nagy Károly
ELTE Elméleti Fizikai Tanszék

A hatáskvantumban valami eddig soha
nem hallott jelentkezik, amely arra van
hívatva, hogy alapjában átalakítsa egész
fizikai gondolkodásunkat.

Max Planck

December 14-én múlt száz éve annak, hogy Max Planck Berlinben a Német Fizikai Társaság ülésén tartott előadásában bemutatta a hőmérsékleti sugárzás törvényének elméleti megalapozását. Ennek során a klasszikus fizika gondolatvilágától idegen feltevést használt. Nevezetesen azt, hogy a rezgő oszcillátor energiája nem folytonosan változik, hanem a frekvenciával arányos kvantumokban. Az univerzális állandóként megjelenő h arányossági tényezőt, mivel hatás dimenziójú mennyiség, hatáskvantumnak nevezte el. A tapasztalattal rendkívül jól egyező formulát már október 19-én előadta, de az elméleti megalapozást, illetve levezetést nem tartotta kielégítőnek. A következő néhány hét fáradságos munkáját végül a Nobel-díjjal és világhírnévvel elismert siker koronázta. Planck az oszcillátor-energia kvantumosságára vonatkozó feltevésével egy új világ felé vezető út kapuját nyitotta ki, amelyen azután elindult a 20. század fizikájának diadalmenete, átívelve az egész századot, és nagyszerű felismerésekkel a rokon tudományokat is megtermékenyítve átalakította a világról alkotott képünket. A technikai és orvosi alkalmazások szinte beláthatatlan sorával pedig jelentősen megváltoztatta az emberek életkörülményeit.
Ahhoz, hogy a kvantumhipotézisnek a fizika fejlődésére kiható jelentőségét és forradalmi voltát megértsük, felidézzük a fizika állapotát a 19. század utolsó évtizedeiben. A newtoni klasszikus mechanika kétszáz éves egyeduralma mellé felsorakozott az elektromágneses jelenségek és az optika átfogó térelmélete, a Maxwell-féle elektrodinamika, ismert volt a hőtan első két főtétele, az energia megmaradását kifejező energia-tétel, és az anyag atomisztikus felépítését - ugyan ekkor még feltevésként - alapul vevő kinetikus gázelmélet. A newtoni klasszikus mechanikának és a Maxwell-elméletnek lenyűgöző hatása volt a kortársakra. A fizikai rendszerek állapotának mérhető mennyiségekkel történő jellemzése, valamint ezek tér- és időbeli változását meghatározó mozgástörvények lehetővé tették a rendszer fizikai állapotának elméleti meghatározását bármely későbbi időben, ha ismerjük a kezdeti állapotot. Ez olyan szellemi teljesítmény, amihez hasonló nem volt ezt megelőzően az emberiség kultúrtörténetében. Azt hiszem, nem tévedek, ha azt állítom, ezzel magyarázható, hogy a kor legtekintélyesebb matematikusai is mechanikai problémákkal kezdtek el foglalkozni. Így keletkeztek a mozgástörvényeknek a newtoni tárgyalásmóddal egyenértékű, de mégis új és néha általánosabb megfogalmazásai. Másrészt nem egy esetben ezek a vizsgálatok kiinduló pontjai lettek a matematika egy-egy fejezetének. (Példaként megemlíthetjük a Fourier-sorok elméletét.) Ugyanez a nagyszerű hatás és kisugárzás elmondható a Maxwell-elméletről is, amely a korábban különálló elektromosságtant, mágnességtant és optikát egységes keretbe foglalva, ugyanazon törvények alapján tárgyalja a fizikai jelenségek igen széles körét. Elméleti úton megjósolta az elektromágneses hullámokat, amelyeket később Heinrich Hertz kísérletileg is kimutatott. Csak megemlítem, hogy Eötvös Loránd is elragadtatással nyilatkozik a klasszikus mechanika csodálatos világáról, amikor azt mondja egyik beszédében, hogy a tudománytörténetnek nincs fényesebb lapja, mint amelyre Galilei mechanikája és Newton gravitációs törvénye van felírva. A mechanikához és elektrodinamikához hozzávéve a fenomenológiai termodinamikát is, elfogultság nélkül megállapíthatjuk, hogy ezek olyan nagyszerű elméletek és oly széles jelenségkört foglalnak magukba, hogy a fizika épülete a befejezettség érzetét keltette a kor tudósaiban. Ennek jellemzésére szoktuk idézni a német fizika professzort, Philipp von Jollyt, aki a hozzá tanácsért forduló fiatal Plancknak azt mondta, hogy a fizika annyira tökéletes és befejezett, hogy ott már nem sok kutatni való akad, nem érdemes erre adni a fejét. Ugyanezt vallotta Lord Kelvin is, amikor 1900-ban egy előadásában ezt mondta, hogy “csak egykét felhőcske van a fizika tiszta kék egén, az egyik a hőmérsékleti sugárzás energiájának frekvencia szerinti eloszlása". Megemlíthette volna még a fényelektromos jelenséget, a gázok vonalas színképét, és a szilárd anyag fajhőjének függését a hőmérséklettől. Ezek ugyanis fontos szerephez jutottak a kvantumelmélet kialakulásának kezdetén. Planck egyetemi tanulmányait ebben a szellemi légkörben végezte. A fizikát a klasszikus fizika nagyszerű mestereitől, Kirchhofftól és Helmholtztól tanulta. A termodinamikát Clausius műveiből sajátította el. Kezdeti tudományos munkássága is a termodinamika területére esik. Több szép eredmény fűződik nevéhez. A hőtan második és harmadik főtételének egyik megfogalmazása tőle származik. Az irreverzibilitás problémája éveken át foglalkoztatta. Ilyen témájú dolgozatait és tudományos esszéit olvasva, azt mondhatjuk, hogy Planck a klasszikus fizika csodálatos eszmevilágának a bűvöletében élt. Ebből fakad az a vallomása, hogy számára az abszolútum keresése tűnik a legszebb tudományos feladatnak. Idősebb kori előadásaiban is úgy emlékezik vissza, hogy az entrópia termodinamikai fogalmában és jelentésében, de még a hatáskvantumban is az abszolútum nyilvánul meg. Azt mondja egyik írásában, hogy "amint a hatáskvantum a kvantummechanikának, ugyanúgy alkotja a fénysebesség a relativitás elméletének az abszolút magját". A klasszikus fizika fogalomvilágához való ragaszkodását azért hangsúlyozzuk, mert már itt a bevezető sorokban rá akarunk arra mutatni, hogy a kvantumhipotézissel ennek a szép klasszikus elméletnek abszolút érvényességét rombolta le. Később még visszatérünk arra, hogy ennek a felismerése milyen nagy problémát okozott neki. Hosszú ideig próbálkozott azzal, hogy a hatáskvantumot beillessze a klasszikus fizika kereteibe. Tudjuk, hogy ez a törekvése nem sikerült, mert a mikrovilágban ettől merőben eltérő törvények érvényesülnek.

E bevezetés után nézzük egy kicsit részletesebben, hogy miről is szól a történet, amely a kvantumelmélet születésének, pontosabban szólva, a kialakulásának a kezdetét meséli el. A hőtan főtételeinek anyagi testekre (különösen gázokra és folyadékokra) való sikeres alkalmazása után a termodinamikai érdeklődés a 19. század utolsó negyedében az elektromágneses sugárzásra irányult. Elsősorban azt vizsgálták, hogy a sugárzást kibocsátó test és a sugárzás milyen feltételek mellett lesz egymással egyensúlyban. A testek atomjainak és molekuláinak hő okozta mozgása által keltett hőmérsékleti sugárzás volt a vizsgálatok tárgya. Ezek olyan általános sajátságok kiderítését tűzték ki célul, amelyek nem függnek a test egyedi tulajdonságaitól. A megfigyelések azt mutatták, hogy a hőmérsékleti sugárzás intenzitása termikus egyensúlyban csak a hőmérséklettől és a frekvenciától függ. A termikus egyensúlyi állapot alatt itt azt értjük, hogy a test időegység alatt átlagosan annyi energiát sugároz ki, mint amennyit elnyel. A kísérleti és elméleti kutatások elsősorban arra irányultak, hogy a sugárzás intenzitásának vagy energiájának frekvenciától való függését adott hőmérsékleten megtalálják. A problémával foglalkozó számos kutató közül Kirchhoff és Wien mindenképpen megemlítendő, mert Planck munkássága szorosan kapcsolódik az övéikhez. Kirchhoff nevéhez fűződik annak a tételnek a megállapítása, miszerint egy belülről teljesen tükröző falakkal határolt üregben kialakult sugárzás intenzitásának frekvencia szerinti eloszlása egyensúlyi állapotban független a kibocsátó testek anyagi minőségétől. A termodinamikai egyensúly beállításához szükség van valamilyen sugárzó testre, amelyik kibocsátja és elnyeli a ráeső sugárzást, így alakítja ki az egyensúlyi állapotot. Ez a test lehet egy szem korom is, de ugyanígy lehet egy modell-test is, például lineáris oszcillátorok sokasága különböző frekvenciákkal. Planck kitűnő kutatói érzékére vall, hogy ezt az utóbbit választotta, mert az oszcillátorra a számítások egyszerűen elvégezhetők. Mivel a termodinamikai kutatásaiban az entrópia központi helyet kapott, így érthető, hogy a sugárzás problematikájához is ezen keresztül nyúlt. Meghatározta a különböző frekvenciájú oszcillátorokból álló rendszer entrópiáját az oszcillátorok rezgési energiájának függvényeként. Az entrópiára olyan kifejezést keresett, amely az energiát logaritmikusan tartalmazza. Ilyen persze többféleképpen megadható, ha nincs olyan elméleti előírás, amely egyértelmű eljárást ad a levezetéshez. Planck a lehetséges módok közül azt választotta, amely határesetben a Wien-féle eloszlásfüggvénybe megy át, de annál általánosabb. Az utóbbi ugyanis nagy frekvenciákra exponenciálisan csökken, jó egyezésben a tapasztalattal, de alacsony frekvenciáknál nagy az eltérés. A Planck által módosított törvény a Wien-félénél jobban egyezik a mérésekkel. Ezt az eloszlásfüggvényt, és a hozzá vezető gondolatmenetet Planck 1900. október 19-én ismertette a Német Fizikai Társaság ülésén “A Wien-féle eloszlási törvény módosításáról" című előadásában.

Ez után Planck teljes idejét arra fordította, hogy ezt a tapasztalattal jól egyező, de lényegében empirikus sugárzási törvényt elméletileg megalapozza. Kirchhoff és Clausius munkásságából ismert volt, hogy ha a sugárzási teret két különböző anyag tölti ki, akkor az egyensúlyi intenzitás a két közegben úgy aránylik egymáshoz, mint a megfelelő fénysebességek négyzeteinek reciproka. Ennél fogva, ha az egyik közegben ismerjük az egyensúlyi intenzitás-eloszlást, akkor ez az összefüggés a másik közegbeli intenzitást is meghatározza. Ennek alapján kézenfekvő volt, hogy először az oszcillátorok egyensúlyi eloszlását határozza meg valamennyi frekvenciára. Pontosabban szólva, azt kell meghatározni, hogyan oszlik el az oszcillátor-rendszer energiája a különböző frekvenciával rezgő oszcillátorokra egyensúlyi állapotban. Ehhez alkalmas eszköznek mutatkozott a Boltzmann-statisztika, amelynek alapján ki lehet számítani azoknak az oszcillátoroknak a számát, amelyek rezgésszáma a v és v+dv intervallumba esik. Ha ezt a számot megszorozzuk a v frekvenciájú oszcillátor átlagos energiájával, akkor az oszcillátor-rendszer egyensúlyi energia-eloszlását kapjuk. A fentebb mondottak szerint ebből már egyszerűen adódik a sugárzás energiájának (vagy intenzitásának) egyensúlyi eloszlása. Mivel az oszcillátor energiája a rezgésszám függvénye, ez az eloszlás egyúttal megadja a keresett frekvenciaeloszlást. A statisztikus mechanika alapján készen van a válasz arra is, hogy mennyi az oszcillátor átlagos energiája. Az ekvipartíció-tétel szerint ez kT (Itt k a Boltzmann-állandót, T pedig az abszolút hőmérsékletet jelenti.) Az így adódó eloszlás adja a Rayleigh-Jeans féle sugárzási törvényt. Ez csak kis frekvenciákra egyezik a tapasztalattal. Egyébként elvileg sem jó, mert eszerint a v frekvenciájú sugárzás energiája a frekvencia négyzetével arányos, és ezért a teljes frekvencia-tartományra vett integrálja végtelen, aminek pedig végesnek kell lennie. Ez annak a következménye, hogy a sugárzási tér a Maxwell-féle térelmélet szerint végtelen szabadsági fokú rendszer, és az előbb említett számítás szerint minden szabadsági fokra ugyanazt az állandó kT átlagos energiát vettük, adott T hőmérsékleten. A mérésekből adódó eloszlási görbe a nagyobb frekvenciákra egyre kisebb, exponenciálisan közelit a zérushoz, amint a frekvenciával a végtelenhez tartunk. Ebből arra lehet következtetni, hogy a magasabb frekvenciákra a kT-nél kevesebb energia jut, vagyis a sugárzási energiára nem érvényes az ekvipartíció-tétel. Ha a statisztikus mechanika tankönyvek megfelelő oldalait megnézzük, észre vesszük, hogy az ekvipartíció-tétel levezetésénél fel van tételezve - a klasszikus fizika gondolatvilágával teljes összhangban -, hogy az energia folytonos függvénye a változóknak. Ennek megfelelően az oszcillátor energiáját is folytonosnak tekintjük, amikor a fenti gondolatmenetet követjük a sugárzási törvény levezetésénél. Plancknak az említett október 19-e utáni hetekben, amikor minden idejét a sugárzási törvény elméleti levezetésére fordította, az a merész ötlete támadt, hogy mi lenne, ha az oszcillátor energiáját nem folytonosnak, hanem adott rezgésszám mellett egyforma kis adagokból, kvantumokból összetettnek, tehát egy 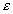energiakvantum egészszámú többszörösének tekintenénk? Mit kapunk ebben az esetben az oszcillátor átlagos energiájára? A számítást elvégezve, meglepetéssel tapasztalta, hogy ez a feltevés jó eloszlás-függvényhez vezet. Ha az 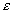energiakvantumot a v frekvenciával arányosnak vesszük <>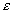 = hv, és az arányossági tényezőként szereplő h állandó értékét alkalmasan választjuk, akkor a kvantumhipotézis alapján számított eloszlásfüggvény tökéletesen ráilleszthető a mérésekkel kapott görbére. h értékét akkor Planck h = 6,5510^-27 erg s-nak találta. A ma mért pontosabb értéke SI mértékrendszerben h = 6,62610^-34 J s. Ezt az univerzális állandót a szakirodalom Planck tiszteletére Planck-állandónak hívja. Mivel ez az állandó hatás dimenziójú mennyiség, Planck hatáskvantumnak nevezte. Még ma is előfordul ez az elnevezés, de gyakoribb a Planck-állandó kifejezés használata. Planck 1900. december 14-én számolt be a sugárzási törvénynek a kvantumhipotézis alapján történt levezetéséről, ugyancsak a Német Fizikai Társaság ülésén "A normálspektrum energiaeloszlási törvényének elmélete" című előadásában. Ezt a napot tekinthetjük a kvantumelmélet születésnapjának. A történeti hűség kedvéért meg kell jegyeznünk, hogy az előadás hallgatói, de maga Planck sem gondolta akkor, hogy a kvantumhipotézis, ami végeredményben az energia kvantáltságát jelenti, merőben ellentmond a fizika addig ismert törvényeinek, a klasszikus fizika egész gondolatvilágának. Planck még jó ideig egy formális matematikai feltevésnek gondolta, és határozottan meg volt győződve arról, hogy a valóságos folyamatokban az energia kibocsátása és elnyelése folytonosan megy végbe. Planck tudományos életrajzában erre így emlékezik vissza. "Amikor a hatáskvantum jelentését entrópia és valószínűség kapcsolatára végérvényesen megállapítottam, még teljesen megmagyarázatlan maradt az a kérdés, hogy milyen szerepet játszik a h állandó a fizikai folyamatok törvényszerű lefolyásánál. Ezért rövidesen elkezdtem próbálkozni, hogy a hatáskvantumot valamiképpen beillesszem a klasszikus elmélet kereteibe, de a hatáskvantum minden ilyen kísérletnek makacsul ellenszegült. Mindaddig, amíg végtelen kicsinek lehetett tekinteni, tehát nagyobb energiáknál és nagyobb hullámhosszaknál, minden a legszebb rendben volt. Általános esetben azonban valahol rés támadt, amely annál feltűnőbb volt, minél kisebb frekvenciákra tértem át. Miután ennek a szakadéknak az áthidalására minden kísérlet meghiúsult, nem volt többé kétség aziránt, hogy a hatáskvantum alapvető szerepet játszik az atomfizikában, és hogy fellépésével új korszak kezdődik a fizikában. A hatáskvantumban ugyanis valami eddig soha nem hallott jelentkezik, amely arra van hívatva, hogy alapjában átalakítsa egész fizikai gondolkodásunkat, amely azóta, hogy Leibniz és Newton megalapozta az infinitezimális számítást, minden kauzális összefüggés folytonosságának feltételezésén alapult. Hiábavaló kísérleteim, hogy a hatáskvantumot valamiképpen belehelyezzem a klasszikus elméletbe, több éven át elhúzódtak, és igen sok munkámba kerültek... Most tehát pontosan tudtam, hogy a hatáskvantum a fizikában jelentősebb, mint ahogy kezdetben hajlamos voltam feltételezni, és teljesen átértettem, mennyire szükséges, hogy teljesen új szemléletet és számítási módszert vezessünk be atomisztikus problémák tárgyalásánál."

A kvantumhipotézis valódi fizikai jelentőségét, vagyis hogy az energia kvantumos szerkezetű, először Einstein ismerte fel. Ennek alapján sikerült megmagyaráznia a fényelektromos jelenséget, amelyet már a múlt század vége felé ismerték, de a fény hullámtermészete alapján nem lehetett megérteni. A jelenség abban áll, hogy ha fémlemezt - különösen alkáli fémet - ultraibolya fénnyel megvilágítunk, elektronok lépnek ki a fém felületéről. A tapasztalat azt mutatta, hogy a kirepülő elektronok sebessége nem függ a megvilágító fény intenzitásától, hanem csak a frekvenciájától (Lenard Fülöp). Nevezetesen, ha növeljük a frekvenciát, megnő az elektronok sebessége is. Másrészt, a fény intenzitásától függ a kilépő elektronok száma. A klasszikus fizika szerint a fémbe behatoló fény energiáját az atom elektronja folytonosan veszi fel, és amikor annyi energiát gyűjtött össze, hogy a fém kötelékéből kiszakadhat, elhagyja annak felületét. Egyszerű számítással meghatározható az időtartam, ami alatt az elektron az atomban a kilépéséhez szükséges energiát összegyűjti. Ehhez 3-4 nap kellene. A megfigyelések viszont azt mutatják, hogy az elektronok a megvilágítást követő százmilliomod másodpercen belül kilépnek a fémből. Ez másként nem értelmezhető, mint úgy, hogy a fény energiája nem folytonos eloszlásban esik a fém felületére, hanem kis adagokban, kvantumokban. A kilépéshez az anyagra jellemző minimális energia szükséges. Nevezetesen az az energia, amivel az elektron kötve van az atomban. Ezt kilépési munkának nevezzük. A fémbe behatoló fénykvantum energiája fedezi a kilépési munkát és az elektron mozgási energiáját. A jelenségnek a fényenergia kvantumos szerkezetén alapuló magyarázata, mint említettük, Einstein nevéhez fűződik. Ezzel indokolták a részére odaítélt Nobel-díjat: Einstein az energia kvantumos szerkezetének a feltevésén még túl is ment, mert az energia kvantumossága mellett az elektromágneses tér impulzusát is impulzuskvantumok összegeként fogta fel. Eszerint az elektromágneses sugárzást hv energiájú, és hv/c impulzusú kvázirészecskéknek tekinthetjük. A kvázi jelző arra utal, hogy bár bizonyos értelemben, illetve körülmények között olyanok, mintha részecskék lennének, de mégsem tekinthetők a szó eredeti értelmében részecskéknek. Ugyanis, a fény hullámelméletéből megismert, kimondottan hullámtulajdonságokkal (mint például az interferencia vagy az elhajlás jelensége) is rendelkeznek. Az elektromágneses sugárzás energia- és impulzuskvantumait Einstein nyomán fotonoknak nevezzük. A sugárzás részecsketulajdonságainak meggyőző kísérleti bizonyítéka volt a Compton-szórás felfedezése. Az elektromágneses sugárzás, (például röntgensugár) szóródik könnyű elemekből álló anyagon, és közben megváltozik a szórt sugárzás frekvenciája a beesőéhez képest. Másrészt a könnyű elemből elektronok repülnek ki. A jelenséget szemléletesen és egyszerűen magyarázhatjuk a fény foton-képe alapján. A beeső foton (mint részecske) az atom elektronjával ütközik, energiájának egy részét átadja az elektronnak. Nagy frekvenciájú fény esetén az elektron kötési energiája elhanyagolható a foton energiája mellett, így a jelenség úgy fogható fel, mintha a foton szabad elektronon szóródna. Az energia- és impulzus-tételből könnyen kiszámítható a fény frekvenciaváltozása, amely jól egyezik a mérési eredményekkel. Az Einstein-féle fotonhipotézis a húszas évek végén kidolgozott kvantumelektrodinamika keretein belül elméleti; és számtalan kísérlettel megerősített igazolást nyert.

Tudománytörténeti érdekessége van a centenáriumi megemlékezések során ismertté lett alábbi megnyilvánulásnak. Max Planck, Walter Nernst, Heinrich Rubens és Emil Warburg 1913-ban ajánlották Einsteint a Porosz Tudományos Akadémia tagjai sorába, és az ajánlásban a munkásságát méltató sorok mellet az is szerepelt, hogy "spekulációiban néha szeret túllőni a célon, mint például a fénykvantum-hipotézisében, ezt azonban nem szabad terhére felróni". Ez szépen mutatja, hogy a kvantumhipotézis nehezen nyert elfogadást a kortárs vezető fizikusok körében. A fenti Planck-idézet is ezt bizonyítja, hogy maga Planck is csak jó pár évvel később ismerte fel feltevésének forradalmi jelentőségét.

A következő fontos lépést szintén Einstein tette meg, amikor 1907-ben a kvantumhipotézist alapul véve megmagyarázta a szilárd anyag fajhőjének zérushoz tartását az abszolút zéruspont közelében. A szilárd anyagra azt a modellt használta, amely szerint az atomok szabályos elrendeződésben harmonikus rezgő mozgást végeznek az egyensúlyi hely körül a hőmérséklettől függően. Einstein azt a legegyszerűbb esetet vette, amelyben mindegyik atom a többitől függetlenül ugyanazzal a frekvenciával rezeg. Nyilvánvaló, hogy ez így nem igaz, mert az egyes atomok mozgása befolyásolja a szomszédokét. Ezzel Einstein is tisztában volt, ezért nem is várt a modellje alapján tökéletes egyezést a tapasztalattal, de a fajhő zérushoz tartását a kvantumhipotézis alapján kvalitatíven értelmezni tudta. Az ő fajhő-képlete exponenciálisan tart a zérushoz, amikor a hőmérsékletet zérushoz közelítjük. A tapasztalattól való eltérés a modell túl egyszerű voltával van kapcsolatban. A rácspontokban levő atomok rezgése nem tekinthető egymástól független harmonikus rezgésnek. A pontosabb tárgyalásnál a kristályrácsnak, mint egésznek a kollektív rezgéseit kell figyelembe vennünk, amelynek során különböző sajátfrekvenciákat kapunk. Az így számított fajhő a tapasztalattal jó egyezésben a hőmérséklet harmadik hatványa szerint változik.

Ezek a példák a 20. század első évtizedének a vége felé már elég meggyőzően mutatták, hogy a kvantumhipotézisben a klasszikus fizikától eltérő törvény mutatkozik meg, és egy új fizika eljövetelének a szükségességét jelzi. Az első Solvay-konferenciát 1911-ben a sugárzás és a kvantumhipotézis témakörének szentelték, és próbálták megérteni annak mélyebb tartalmát. A résztvevők érzékelték, hogy most valami változás következik be a fizika további alakulásában, de hogy merre tart és milyen nagymértékben változtatja meg a világról alkotott képünket, azt nem is sejtették. Arra sem gondoltak, hogy az atomok szerkezetéről fog hírt hozni. A nagy fordulat a fejlődésben két évvel később következett be, amikor Niels Bohr előállt a hidrogén-atomra vonatkozó elméletével. Ez az elmélet már tudatos szakítás volt a klasszikus fizikával az atomok világában. A hatáskvantum a Bohr-elméletben a stacionárius elektronpályák kiválasztásában jelenik meg. Eszerint csak olyan pályákon kering az elektron, amelyekre vonatkozóan az impulzusnyomaték a hatáskvantum egészszámú többszöröse. Sugárzás akkor következik be, amikor egyik pályáról egy alacsonyabb energiájúra ugrik. A közben kibocsátott sugárzás frekvenciája az energiakülönbségnek és a hatáskvantumnak a hányadosával egyezik meg. Ezek a kijelentések a klasszikus fizikán nevelkedett és annak gondolatvilágában alkotó fizikusok számára szinte istenkáromlásként hatottak. A bizalom az elmélet iránt akkor kezdett éledezni, amikor az atomok vonalas színképét sikerült a megfigyelésekkel összhangban megmagyaráznia. Már ennek is bámulatos hatása volt, de még ennél is nagyszerűbbnek tűnt az elemek periódusos rendszerének az értelmezése. Az elmélet kijelentéseit igazolni szándékozó kísérletek, a mágneses nyomaték kvantáltságának és a spinnek a felfedezése mellett arra is rámutattak, hogy a Bohr-elméletnek több hiányossága van. Elég azt megemlíteni, hogy csak a hidrogénatomra lehet alkalmazni. Már a következő elemnél, a héliumnál sem járt sikerrel.

Az atomok és molekulák fizikájának elméletére még több mint tíz évet kellett várni. Persze közben nem tétlenkedtek a fizikusok, a mikrovilág sok szép új jelenségét fedezték fel, de az ezeket is magukba foglaló és magyarázó elmélet még hiányzott. Az igazán nagy jelentőségű lépést Werner Heisenberg tette meg 1925-ben a kvantummechanika megalkotásával. Őt követte pár hónapon belül Ervin Schrödinger a hullámmechanikával. Bár a két tárgyalásmód teljesen különböző, de miként azt Schrödinger kimutatta, a kettő egymással egyenértékű. Meg kell még említeni Paul Dirac nevét; aki a kvantummechanika elvontabb megalapozását adta. Az utóbbi mindkettőt magába foglalja, ha az operátorokat mátrixok, illetve differenciáloperátorok alakjában állítjuk elő. Az új elmélet fizikai értelmezésének kialakításában nagy szerepe volt az említett alkotók mellet Niels Bohrnak, Max Bornnak, Pascal Jordannak és Wolfgang Paulinak. A hatáskvantum a kvantummechanikában is már az alapvetésnél megjelenik. Egyrészt a Heisenberg-féle felcserélési törvényekben, amelyek axiómaként megszabják, hogy az egymáshoz kanonikusan konjugált mennyiségekhez milyen operátorok rendelendők, másrészt a mozgástörvényként szereplő dinamikai egyenletben. Fontos következménye az elméletnek, hogy az egymással fel nem cserélhető operátorokkal reprezentált fizikai mennyiségek egyidejűleg nem mérhetők meg tetszőleges pontossággal. A mérési hibák szorzata arányos a hatáskvantummal. Ezek a határozatlansági összefüggések a hatáskvantumnak szemléletes jelentést adnak még az eléggé elvont kvantummechanikában is.

A kvantummechanika elveit és módszereit Heisenberg és Pauli kezdeményezésére kiterjesztették először az elektromágneses térre, majd más fizikai erőterekre. Az így adódó kvantum-elektrodinamikában az elektromágneses sugárzási tér energiája és impulzusa hv, illetve hv/c kvantumok összegeként adódik. A sugárzás kvantumossága, ami száz évvel ezelőtt hipotézis volt, az elméletnek következménye lett.

A Planck által felfedezett hatáskvantum a 20. század fizikájának egyik legfontosabb univerzális állandója. A kvantumhipotézis volt a 20. század egyik legragyogóbb, és leghatásosabb fizikai elméletének, a kvantummechanikának kiinduló pontja. Fizikai világképünk radikális megváltozását eredményező hatásán kívül az alkalmazások egész sorát lehetne felsorolni a kémia, a technika, a biológia vagy az orvostudomány területéről. Ennek illusztrálására legyen itt csupán egyetlen példa. A különféle anyagok elektromos vezetési tulajdonságainak kvantummechanikai magyarázata vezette Bardeent, Wigner Jenő tanítványát a tranzisztor elvének a felfedezéséhez. Erre alapozva indult meg a modern elektronikai kutatás, és az eredmények műszaki alkalmazása, ami mára a szórakoztató elektronikai iparral, valamint a számítógépekkel teljesen átalakította az emberi kapcsolatokat, és jelentősen megváltoztatta az emberek viszonyát a munkához. A számítógépes világhálón keresztül kitárult előttük a világ.

A kvantummechanikának az erőterekre történt kiterjesztése, a kvantumtérelmélet az anyag legelemibb alkotó részeit, azok között ható kölcsönhatásokat, az elemi részek fizikáját kutatja. Ezek a hozzá kapcsolódó kísérleti vizsgálatokkal együtt jelentik a 20. század utolsó néhány évtizedének kutatásait a fizika fejlődésének abban a fő vonulatában, amely Newton Princípiájával kezdődött, Planck kvantumhipotézise óta felerősödve, a fizika fundamentális kérdéseire keresi a válaszokat.

A huszadik század fizikája, nagyszerű szép eredményeivel és azok gyakorlati alkalmazásaival, meggyőzően bizonyítja, hogy a kvantumhipotézis a legragyogóbb fizikai felismerések egyike. Planck ezzel nemcsak ajtót nyitott egy addig nem ismert új világra, de a hatáskvantummal kulcsot is adott a kutatók kezébe a további zárak felnyitásához.

_____________________________

A Magyar Tudományos Akadémián 2001. január 17-én tartott előadás.