Fizikai Szemle honlap |
Tartalomjegyzék |
Meggyőződésünk, hogy csak olyan tanárok tudják jól tanítani a fizikát (és bármi mást), akik sokszorosan többet tudnak, mint amit éppen meg kell tanítaniuk. Ezért a Fizika tanítása rovatba várunk olyan cikkeket is, amelyek színvonala túlmutat a szorosan vett középiskolai szinten, és amelyek ezzel a fizikatanárok szakmai fejlődését segítik, nem-hivatalos "továbbképzést" jelentenek. Horváthy Péter cikke egy klasszikus feladat különböző fizikai alapelvekből kiinduló megoldásán keresztül elvezet a bolygómozgás 17. századi ismereteitől egészen a 19. század végén, a 20. század elején felfedezett belső szimmetriákig.
Ujvári Sándor
P.A. Horváthy
Laboratoire de Mathématiques et de Physique Théorique
Université de Tours,
Franciaország
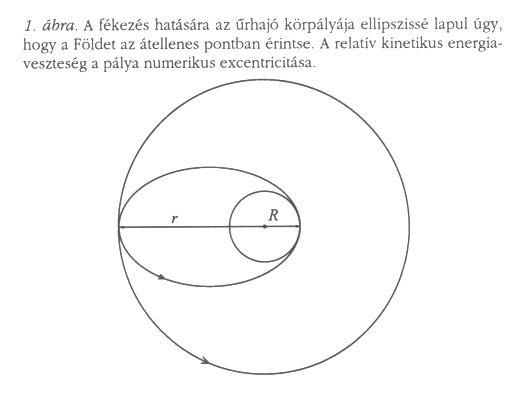
Az 1969. évi Eötvös-verseny első feladata a következőképpen hangzott: ![]() g tömegű, R = 3600 km rádiuszú égitest felszíne felett 400 km magasan egy űrhajó kering körpályán. Fékezőrakétáját rövid ideig menetiránnyal szemben működtetve olyan ellipszispályára tért, amelyben az égitest átellenes pontján elérte annak felszínét. A fékezéskor mozgási energiájának hányad részét kellett elveszítenie?
g tömegű, R = 3600 km rádiuszú égitest felszíne felett 400 km magasan egy űrhajó kering körpályán. Fékezőrakétáját rövid ideig menetiránnyal szemben működtetve olyan ellipszispályára tért, amelyben az égitest átellenes pontján elérte annak felszínét. A fékezéskor mozgási energiájának hányad részét kellett elveszítenie?
A feladat megoldását Vermes Miklós gyűjteménye [1] csak vázlatosan tárgyalja, pedig behatóbb vizsgálat további érdekes tulajdonságokat tár föl, s ez a probléma mélyebb megértéséhez vezet. A lényeg a következő. Fékezés ideje rövid, s így utána az űrhajó térbeli helyzete gyakorlatilag változatlan. A sebesség csökkenése miatt a vonzóerő túlsúlyba kerül és a mozgást "befelé görbíti": a pálya
![]()
fél nagytengelyű ellipszis (itt r a körpálya sugara).
A feladat a tér egyazon pontján átmenő elliptikus és körtrajektóriák aphéliumi kinetikus energiájának összehasonlítása. A megoldás kulcsa a következő állítás: Az elliptikus és körmozgás [aphéliumi] kinetikus energiáinak aránya:
azaz ![]() a fékezés utáni ellipszis perihélium-távolságának és fél nagytengelyhosszának aránya.1 Figyeljük meg, hogy az eredmény mindkét égitest tömegétől független és csak a pályák geometriai méreteitől függ. Innen már következik a feladatban kitűzött kérdésre a válasz:
a fékezés utáni ellipszis perihélium-távolságának és fél nagytengelyhosszának aránya.1 Figyeljük meg, hogy az eredmény mindkét égitest tömegétől független és csak a pályák geometriai méreteitől függ. Innen már következik a feladatban kitűzött kérdésre a válasz:
Tekintve, hogy
![]()
az excentricitás, (2) az ![]() =
e/a alakban is írható: a relatív kinetikus energiaveszteség a pálya numerikus excentricitása, azaz a kör ellipszissé lapulásának mértéke. A fenti adatokkal számolva, az eredmény
=
e/a alakban is írható: a relatív kinetikus energiaveszteség a pálya numerikus excentricitása, azaz a kör ellipszissé lapulásának mértéke. A fenti adatokkal számolva, az eredmény ![]() = 1/19.
= 1/19.
Az alábbiakban (1) különböző szempontból való bizonyítását adjuk. Bizonyításaink az egyszerűbbtől a bonyolultabb, az elemitől a több előismeretet kívánó felé haladnak.
Mivel a válasz nyilvánvalóan nem függ az űrhajó tömegétől, válasszuk utóbbit egységnyinek.
I. megoldás: Kepler törvényeivel
Első megoldásunk lényegében azonos Vermes Miklóséval [1]. A körmozgás törvénye szerint
![]()
(3)
(ahol f a gravitációs állandó), s így a körmozgás kinetikus energiája:
![]() .
.(4)
A keringési idő (négyzete) eszerint
Kepler III. törvényét a kör- és elliptikus mozgásokra alkalmazva, megkapjuk a fékezés utáni keringési időt:

Az ellipszis területe ![]() ab, ahol b a fél kistengely.
ab, ahol b a fél kistengely.
![]()
s ezért a terület
![]()
Így a területi sebesség, mely Kepler II. törvénye szerint konstans:
![]() .
.
Aphéliumban
![]() ,
,
s így a fékezés utáni sebesség
![]()
A fékezés utáni mozgási energia tehát
![]()
ahonnan(1) következik.
II. megoldás: energia- és impulzusmegmaradásból
Második megoldásunk az energia- és impulzusmegmaradás tételén alapul. Fékezés után a kezdeti ("aphéliumi") és becsapódási ("perihéliumi") sebességeket va és vp-vel jelölve, az energia- és az impulzusmegmaradási (Kepler II.) tételek szerint:
![]()
![]() .
.
A számunkra érdektelen perihéliumi sebességet eliminálva megkapjuk az elliptikus mozgás (9) kinetikus energiájának képletét.
III. megoldás; a bolygómozgás összenergia-képletének felhasználásával
Harmadik megoldásunk egy, a KöMaL-ban korábban kitűzött feladatra [2] támaszkodik.
Lemma: Legyen egy bolygó fél nagytengelye a és pillanatnyi távolsága r. Ekkor a sebesség a vizsgált pontban:
![]()
A bizonyítás lényege (lásd pl. [3] 21. fejezet 5, 98. o.) az, hogy a teljes energia
![]()
s ezért a teljes energia fordítva arányos a nagytengely hosszával:
![]()
Ekkor (12) épp az energiamegmaradás. Megjegyzendő, hogy (13) konzisztens a körmozgás esetében (4)-ből levezethető képlettel.
Körpályánál a = r, a fékezés utáni ellipszispálya esetén pedig a = ( r+ R )/2, amelyet (12)-be írva (4)-et, illetve (9)-et kapjuk.
Még egyszerűbben, fékezéskor az összenergia változása a kinetikus energiák változása - hiszen a potenciális energia csak a pozíciótól függ -, ami a kétfajta mozgásnál ugyanaz. Így (13) szerint
![]()
Ide fM/2r helyére (4) szerint ![]() -t írva, közvetlenül
(2)-t kapjuk.
-t írva, közvetlenül
(2)-t kapjuk.
Érdemes megjegyezni, (12) szerint a pálya r pontjában a mozgási és helyzeti energia aránya
![]()
Körpálya esetén, illetve a fékezési utáni elliptikus mozgásnál ezért
![]()
leosztva újra (1)-et kapjuk.
IV. Kapcsolat Kepler III. törvényével
A megoldáshoz fűzött megjegyzésében az eredményt Vermes a "kinetikus energia kistengely-függetlenségével" magyarázza, mely szerinte Kepler III. törvényével állna kapcsolatban. Ez azonban nem így van: míg - (13) értelmében - a bolygómozgás összenergiája csak a pálya nagytengelyétől függ, a kinetikus és helyzeti energia összenergiából való részesedésére ez már nem igaz. (15) szerint:
![]()
Az ellipszis adataival kifejezve, az aphéliumi kinetikus energia
![]()
ami függ a kistengelytől. Kepler III. törvénye ugyanis nem a mozgási energiák kistengely-függetlenségét vonja maga után (ami, tekintve a mozgási energia helyfüggését, egyszerűen értelmetlen állítás lenne), hanem a következőket [4]: ha egy bolygómozgást a fókuszból ![]() -szorosra nyújtunk és közben az időt
-szorosra nyújtunk és közben az időt ![]() -nel szorozzuk,
-nel szorozzuk, ![]() akkor újra egy lehetséges bolygómozgást kapunk; az egymásnak megfelelő pontokban a kinetikus és a potenciális energia úgy aránylik egymáshoz, mint a geometriai méretek reciprokai:
akkor újra egy lehetséges bolygómozgást kapunk; az egymásnak megfelelő pontokban a kinetikus és a potenciális energia úgy aránylik egymáshoz, mint a geometriai méretek reciprokai:
![]()
Ez a formula valóban emlékeztet (1)-re, melynek jobb oldala eszerint úgy lenne interpretálható, mint a fékezés utáni ellipszis fél nagytengelyhosszának (fordított) aránya egy másik, eddig nem vizsgált, elliptikus mozgás fél nagytengelyhosszával. Utóbbi R, a perihélium-távolság lenne (s ezért a központi égitest ottléte miatt csak hipotetikus). Az új, R fél nagytengelyű elliptikus mozgás aphéliumi kinetikus energiája megegyezne az eredeti körmozgás kinetikus energiájával - de nem ez volt a kérdés. A félreértés eredete R összekeverése r-rel, a körmozgás "fél nagytengelyével" (lásd 1. lábjegyzet).
Vermes érvelése javítható: zsugorítsuk össze az eredeti körmozgást úgy, hogy az új sugár épp a fékezés utáni elliptikus trajektória nagytengelye legyen, azaz tekintsük az eredeti körmozgás
![]()
-szeres zsugorítását. Ennek összenergiája (18) szerint (és (13)-mal konzisztensen)
![]()
(13) szerint azonban ugyanennyi a fékezés utáni elliptikus mozgás összenergiája is,![]() , hiszen a nagytengelyek egyenlőek. Így
, hiszen a nagytengelyek egyenlőek. Így
![]()
amiből (16)-ot használva újra (1)-et kapjuk.
Jegyezzük meg, hogy Kepler III. törvénye önmagában nem volt elegendő ahhoz, hogy a fékezés utáni elliptikus és a "zsugorított körmozgás" összenergiáinak egyenlő voltát levezessük. Ehhez tudnunk kellett, hogy az összenergia csak a nagytengely hosszának függvénye: (13) Kepler III. törvényénél erősebb állítás.
V. megoldás
Használjuk a mechanika Newton-féle törvényének a részecskével együtt mozgó koordinátarendszerben felírt alakját. Tetszőleges formájú pálya esetén
(3) általánosítása ([3], 3. fej. 20. o.) szerint a gyorsulás normális komponense v2/![]() , ahol
, ahol ![]() a vizsgált pontbeli görbületi sugár. Az ellipszis extremális pontjaiban a gyorsulás normális irányú,2 s ezért
a vizsgált pontbeli görbületi sugár. Az ellipszis extremális pontjaiban a gyorsulás normális irányú,2 s ezért
![]()
Körre ![]() = r, s így
= r, s így
![]()
hiszen az erő mindkét mozgás esetén ugyanaz. Szavakban: a kinetikus energiák aránya a görbületi sugarak aránya. De az ellipszis extremális pontjaiban a görbületi sugár az ellipszis paramétere,
![]()
'
ahonnan újra (1) következik. Az eredmény megerősíti előző intuíciónkat: a sebesség csökkentése növeli a görbületet.
Az erő konkrét alakját, f M / r2-et (19)-be beírva a fékezés utáni sebesség meghatározható:
![]()
de erre az általunk vizsgált esetben nincs szükség, elég volt tudni, hogy a trajektória ellipszis.
VI. megoldás; a Runge-Lenz-vektor felhasználásával
A II. megoldáshoz hasonló levezetés kapható az úgynevezett Runge-Lenz-vektor
K = v ![]() L - f M
L - f M ![]()
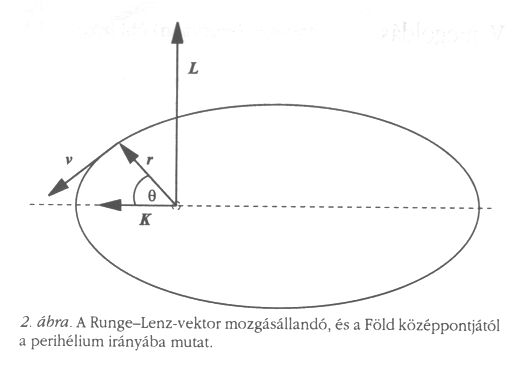
segítségével is, ahol L = r x v a megmaradó impulzusmomentum és ![]() a Naptól a bolygóhoz mutató r rádiuszvektorral párhuzamos egységvektort jelöli. Ezt a vektort Laplace vezette be (Laplace: "Traité de Mécanique Céleste", Paris, 1799), majd Hamilton fedezte fel újra 1845-ben. Az elnevezés eredete, hogy K (feladatként) felbukkan C. Runge 1919-es vektoranalízis-könyvében. 1924-ben W. Lenz, majd 1926-ban W. Pauli a hidrogénatom kvantummechanikai leírásánál használta. Eredetét és alkalmazásait például a fiatalon elhunyt Györgyi Géza tanulmányozta a hatvanas évek végén [5].
a Naptól a bolygóhoz mutató r rádiuszvektorral párhuzamos egységvektort jelöli. Ezt a vektort Laplace vezette be (Laplace: "Traité de Mécanique Céleste", Paris, 1799), majd Hamilton fedezte fel újra 1845-ben. Az elnevezés eredete, hogy K (feladatként) felbukkan C. Runge 1919-es vektoranalízis-könyvében. 1924-ben W. Lenz, majd 1926-ban W. Pauli a hidrogénatom kvantummechanikai leírásánál használta. Eredetét és alkalmazásait például a fiatalon elhunyt Györgyi Géza tanulmányozta a hatvanas évek végén [5].
K-t az idő szerint differenciálva, a
![]()
relációt és a mozgásegyenletet felhasználva beláthatjuk, hogy K = 0, azaz K mozgásállandó. K-t L-lel skalárisan szorozva nullát kapunk, s ezért K a pályasíkban fekszik, hiszen L erre merőleges és a Naptól a perihélium-pont felé mutat. (22)-t r-rel szorozva,
![]()
Kihasználva, hogy
![]() ,
,
![]() innen
innen
![]()
ahol ![]() a K és az r szöge.
(23) egy p paraméterű,
a K és az r szöge.
(23) egy p paraméterű, ![]() numerikus excentricitású kúpszelet polárkoordinátás egyenlete.
numerikus excentricitású kúpszelet polárkoordinátás egyenlete.
A minket érdeklő problémához visszatérve, figyeljük meg, hogy pálya extremális pontjaiban
![]()
ahol ệ a Naptól a perihélium-pont felé mutató egységvektor. L hossza nyilván L = vp rp = va ra [lásd (11)]. A perihélium-sebességet eliminálva:
![]()
Körpályánál ra = rp = r és (4)-et kapjuk, a fékezés utáni ellipszis esetében pedig rp = R-et és ra = r-et írva, újra megkapjuk az aphéliumi kinetikus energia (9) képletét. (24)-et négyzetre emelve belátható, hogy
![]()
s így (13) miatt K= f M![]() . Ezért
(23) a bolygópálya szokásos formulájával [3] egyenértékű. K értékét ismerve, a feladat megoldása újra megkapható:
(24) szerint
. Ezért
(23) a bolygópálya szokásos formulájával [3] egyenértékű. K értékét ismerve, a feladat megoldása újra megkapható:
(24) szerint
![]()
s ezért
![]()
De f M / r (4) szerint 2![]() , ahonnan újra
(1)-et kapjuk.
, ahonnan újra
(1)-et kapjuk.
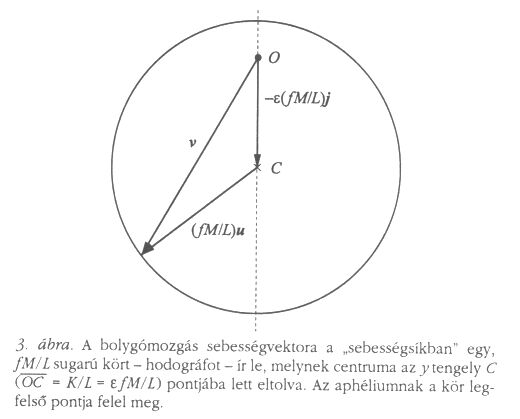
VII. megoldás: a hodográf segítségével
A sebességvektort minden pillanatban a "sebességsík" egy O pontjából felmérve, a holográfot kapjuk. A bolygómozgás hodográfja kör. Ennek egyszerű bizonyítását kapjuk, ha az impulzusmomentumot vektoriálisan szorozzuk a Runge-Lenz-vektorral. A kettős vektorszorzatot kifejtve, ![]() = 0-t felhasználva
= 0-t felhasználva
![]()
ahol u az ![]() -ből az L mint tengely körüli, óramutató járásával ellentétes irányú 90°-os forgatással kapott egységvektor. De L xK = -LKj, ahol j a koordináta-síkban az y tengely irányába mutató egységvektora. Ide K = f M
-ből az L mint tengely körüli, óramutató járásával ellentétes irányú 90°-os forgatással kapott egységvektor. De L xK = -LKj, ahol j a koordináta-síkban az y tengely irányába mutató egységvektora. Ide K = f M![]() -t írva, a sebességvektor kifejezhető:
-t írva, a sebességvektor kifejezhető:
![]()
Az ![]() egységvektor a mozgás során körbefordul, s ugyanezt teszi (90°-kal "előreforgatva") u. Így
(28) első tagja egy f M / L sugarú kör, melynek centrumát a második tag eltolja az y tengely -K / L = f M
egységvektor a mozgás során körbefordul, s ugyanezt teszi (90°-kal "előreforgatva") u. Így
(28) első tagja egy f M / L sugarú kör, melynek centrumát a második tag eltolja az y tengely -K / L = f M![]() / L "magasságú" (pontosabban mélységű) C pontjába. A sebességvektor végpontja - a hodográf - tehát egy f M l L sugarú, excentrikus kör, mint állítottuk. Amennyiben a pálya kör, akkor K = 0 és a hodográfkör centruma a sebességsík origója; ekkor nyilván
/ L "magasságú" (pontosabban mélységű) C pontjába. A sebességvektor végpontja - a hodográf - tehát egy f M l L sugarú, excentrikus kör, mint állítottuk. Amennyiben a pálya kör, akkor K = 0 és a hodográfkör centruma a sebességsík origója; ekkor nyilván ![]() .
.
A sebesség a kör - perihéliumnak megfelelő - alsó pontjában a legnagyobb és az aphéliumnak megfelelő felső pontban a legkisebb. Ekkor u függőlegesen felfelé mutat, ua = j . A sebességvektor hossza = (sugár) - (a centrum origótól való távolsága), ahonnan (27) következik. (Ugyanezt kapjuk, ha (28)-ba L = va ra-t írjuk).
Összefoglalásként, tekintsük át különböző megoldási módszereinket.
 L = 0, és
(26) az O(4) "dinamikus szimmetria" Casimir-relációi.
L = 0, és
(26) az O(4) "dinamikus szimmetria" Casimir-relációi.A feladat egy variációját az 1972-es Országos Középiskolai Tanulmányi Verseny II. fordulójában tűzte ki Bodó Zalán. Példánk hasonló egy korábbi a KöMaL-feladathoz [7] is: Az 1966-os Ikeya-Seki-üstökös az 1967. évi csillagászati évkönyv szerint Nap-rádiusznyi, azaz 700000 km távolságban haladt el a Nap felszíne fölött, és keringési ideje 1000 év. Mennyi a sebessége napközelben és naptávolban?
A fenti módszerek bármelyikét alkalmazva, a perihéliumi, illetve aphéliumi sebességek képlete
![]()
Az üstökös fél nagytengelyhossza Kepler III. törvényéből a Föld adataival (Tf = 1 év és af = 150  106 km) határozható meg: a = 100 af. Esetünkben a- e = 2R, s így e = a - 2 R, amiből vp = 437 km/s, va = 20,4 km/s.
106 km) határozható meg: a = 100 af. Esetünkben a- e = 2R, s így e = a - 2 R, amiből vp = 437 km/s, va = 20,4 km/s.
Irodalom
1. VERMES MIKLÓS: Az Eötvös-versenyek feladatai. I. 1959-1988. Nemzeti Tankönyvkiadó, Typotex Kft. 1997. 56-58. o.
2. Középiskolai Matematikai Lapok 1962/8-9. szám.
3. BUDÓ ÁGOSTON: Mechanika - Negyedik kiadás. Tankönyvkiadó, Budapest (1965).
4. L. LANDAU, J. LIFSIC: Mechanika
5. GYÖRGYI GÉZA: A Kepler problémáról - Fiz. Szemle 15 (1965) 74; A Kepler-probléma "rejtett" szimmetriáiról - Fiz. Szemle 18 (1968) 142 (1968); Dinamikai szimmetriák - (tud. doktori értekezés) Magyar Fizikai Folyóirat 20 (1972) 45
6. D.L. GOODSTEIN, J.R. GOODSTEIN: Feynman's lost lecture. The motion of the planets around the Sun - Vintage 1997.
7. Középiskolai Matematikai Lapok 1967/10. szám, 670. Feladat
_____________________________
1 Vermes állításával ellentétben, ![]() nem a nagytengelyek aránya, hiszen a körmozgás sugara nem R, hanem r
nem a nagytengelyek aránya, hiszen a körmozgás sugara nem R, hanem r