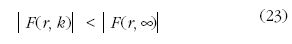Fizikai Szemle 2004/12. 397.o.
A KLASSZIKUS GRAVITÁCIÓELMÉLETRŐL
Gábos Zoltán
Babes¸-Bolyai Tudományegyetem
Kolozsvár, Románia
A gravitációs kölcsönhatást (a gravitációt) ma a leggyengébb
alapvető kölcsönhatásnak tekintjük. Számolni kell
vele, valahányszor legalább az egyik kölcsönható partner
tömege elég nagy. A testek súlyának okozója fontos szerepet
játszik a Világegyetem nagyléptékű szerkezetének
alakításában, a kozmikus családok - például a Naprendszer
- összetartásában. Összehúzó, tömörítő hatása döntő
szerepet játszott és játszik a csillagok világában. Így nem
véletlen, hogy a gravitáció és a világmodellek története
szorosan egybefonódott.
A fejlődés során a feladatukat teljesítő, de lehetőségeiket
kimerítő modelleket új, a valóságot jobban tükröző
modellek váltják fel. Ez nem akadálymentes folyamat. A
megszokotthoz való ragaszkodás lassítja azoknak a merevítő
elemeknek, akadályoknak az eltávolítását, amelyek a
haladást gátolják. Ezt a tényt a gravitáció története is tanúsítja.
A következőkben a klasszikus gravitációelmélet történetének
vázlatos bemutatására vállalkozunk. Történetünket
a speciális relativitáselmélet megjelenésével, az 1905-ös évvel zárjuk.
A newtoni elméletig vezető út
Az antik világ természettudományos ismereteinek összefoglalására
elsőként a görög tudósok vállalkoztak. Világmodelljeik
között megtaláljuk Ptolemaiosz geocentrikus,
de ugyanúgy Arisztarkhosz heliocentrikus modelljét is.
A XVI. század közepéig a geocentrikus modellt használták.
A Földhözkötöttség, a mindennapos tapasztalatok
ennek a modellnek kedveztek. Élesen elkülönítették a
tökéletesnek vélt égi, és a változó, tökéletlennek minősített
földi világot. A gömbölyűnek és mozdulatlannak tekintett
Földnek jutott a Világegyetem központjának a
szerepe. A Föld körül egyenletesen forgó égi világ szféráiban kapott
helyet a Nap, a Hold, öt bolygó (Merkúr,
Vénusz, Mars, Jupiter, Szaturnusz) és az állócsillagok.
Használták a tökéletes és természetes (külső beavatkozást
nem igénylő) mozgás fogalmát. E szerep az egyenletes
körmozgásnak jutott. A vándorló csillagnak tekintett
öt bolygó rendellenesnek tekintett mozgását egymásba
fonódó körmozgásokkal magyarázták.
A modell hívei sikerrel teljesítették azt a feladatot,
hogy az égitestek látszólagos mozgásával kapcsolatban
minél több információt nyerjenek. Ezek az adatok a továbbiak
szempontjából hasznosnak bizonyultak. A gravitáció
szempontjából a mértékszámmal jellemezhető súlyfogalom
megjelenése is döntő fontosságú volt. Archimédesz
a fajsúly és súlypont fogalmakat is ismerte.
A bolygómozgás törvényeinek megállapítására a geocentrikus
modell alkalmatlannak bizonyult. Az előrelépés
terén az első lépést N. Kopernikusz tette meg 1543-ban.
Modelljében a Nap a központi égitest, körülötte keringenek
a bolygók, amelyek köre a Földdel gazdagodott. Az
állócsillagok látszólagos mozgását a Föld forgásával magyarázta.
A Föld egy kísérővel maradt, de később ez a
kiváltsága is elesett, amikor G. Galilei 1610-ben Jupiter
körül keringő holdakat fedezett fel. A körpálya kitüntetett
szerepéhez ragaszkodó Kopernikusz nem tudta hasznosítani
heliocentrikus modelljének előnyeit, de a Föld-Nap
szerepcserével rést ütött az égi és földi világ közé emelt
válaszfalon.
J. Kepler elsőként merte tagadni a körpálya kitüntetett
szerepét. Nagymértékben hasznosította Tycho de Brahénak
a látszólagos bolygópályákra vonatkozó megfigyelési
adatait (ezek nagyrészt a Mars bolygóra vonatkoztak).
Kepler a bonyolult körpályasokaságot egyetlen ellipszispályával
cserélte fel. A Napot az ellipszis gyújtópontjába
helyezte. Mindezt az 1609-ben közölt, nevét viselő első
törvényben rögzítette. A tíz évvel később megfogalmazott
harmadik törvény fontos szerepet játszott a gravitáció történetében.
Eszerint a bolygó keringési idejének négyzete
egyenesen arányos a pálya fél nagytengelyének köbével:

ahol C az összes bolygókra azonos értékű.
Kepler törvényei több okból is ösztönözték a továbblépést.
A törvények elméleti megalapozást igényeltek. Az
(1) alatti kapcsolat arra utalt, hogy a bolygók pályáját a
Nap alakítja, ezért a Nap hatásának vizsgálatát Kepler a
megoldandó feladatok körébe sorolta. A maga idejében ő
ezzel a feladattal nem tudott megbirkózni. Az előrelépést
a "földi fizika" eredményei készítették elő.
Döntő fontosságú volt annak a felismerése, hogy a
természetes mozgás megnevezés az egyenes vonalú
egyenletes mozgást illeti. Ezt elsőként R. Descartes állította
1633-ban. Nyilvánvalóvá vált, hogy az ellipszispályán
vagy akár a körpályán történő mozgás fenntartása külső
hatást igényel.
A mozgások leírása szempontjából igen fontosnak
bizonyultak Galilei eredményei. Értelmezte a pillanatnyi
sebesség és gyorsulás fogalmát és kísérletekkel igazolta,
hogy a szabadesés egyenletesen gyorsuló mozgás. Kimutatta,
hogy a Föld középpontja felé tartó test g gyorsulása
nem függ az eső test anyagi minőségétől és súlyától.
Az ingamozgást is vizsgáló Ch. Huygens 1673-ban arra
a következtetésre jutott, hogy az egyenletes körmozgás
esetében egy a középpont felé mutató centripetális gyorsulással
kell számolni, amelynek nagyságát

adja, ahol R a kör sugarát és v a kerületi sebességet jelöli.
(Ezt az összefüggést 1666-ban I. Newton is levezette, de
Huygens a közlésben megelőzte.)
A "földi fizika" felsorolt eredményei lehetővé tették
azt, hogy a Napnak bolygókra gyakorolt hatásáról többet
tudjanak mondani. A bolygók mozgásának vizsgálata
a figyelem középpontjába került. Egy 1666-tal kezdődő,
1687-ig tartó időszak következett, amelyet a
klasszikus gravitációelmélet virágkorának tekinthetünk.
E szakasz vezéregyénisége I. Newton volt, aki 1687-ben
megjelent Philosophiae naturalis principia mathematica
című művében összegezte saját és kortársai eredményeit.
A következőkben az elvi jelentőségű eredményekből
válogatunk.
I. Newton, E. Halley és C. Wren, egymástól függetlenül,
az (1) és (2) alattiakat hasznosították. Körpálya közelítést
használva, (1)-ben a helyett a körpálya sugarát, R-et
írva, az egyenletes körmozgásra érvényes

összefüggést is figyelembe véve, az
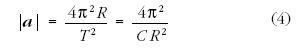
kapcsolathoz jutottak. Így állíthatták, hogy a bolygókat
a Nap vonzóhatása tartja meg pályájukon, és a hatás
erőssége a Naptól mért távolság négyzetével fordítottan
arányos. R. Hooke más úton jutott ugyanerre a következtetésre.
Állította, hogy a Nap hatása radiális irányban
terjed szét, és ezért a távolság négyzetével fordított
arányban gyengül. I. Newton elsőként ismerte fel, hogy
a szabadesés és a Hold Föld körüli mozgása esetében
egyazon hatással kell számolni. Figyelembe vette, hogy
a hatás erőssége a távolság négyzetével fordítottan arányos,
és így kör alakú Holdpálya esetében (4) felhasználásával a
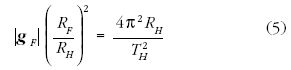
kapcsolathoz jutott, amelyben RF a Föld-, RH a Hold-pálya sugarát,
gF a szabadesés gyorsulását jelzi a földfelszín
közelében, TH a Hold keringési ideje. Amikor Newton az
(5) alatti kapcsolatot megállapította, RF- fel és RH -val kapcsolatban
nem álltak rendelkezésére pontos adatok. Miután ezek
birtokába jutott, (5) helyességéről maga is
meggyőződhetett.
A fentiekben a gravitációs hatás esetében jelentkező
gyorsulást vettük tekintetbe. Miután kiderült, hogy a súly
erő jellegű mennyiség, a gravitációs erő kérdése is napirendre
került. A súly és a nehézségi gyorsulás egyirányú
vektorok, így közöttük

alakú kapcsolatot lehetett létesíteni. Az m skaláris
mennyiséget ma súlyos tömegnek nevezzük. E mennyiség
a test gravitációs kapcsolatot létesítő képességét
méri. A (6) kapcsolat egyben arra is utalt, hogy a gravitációs
erő arányos a gravitációs hatásnak kitett tárgy
tömegével.
Newton arra az esetre is gondolt, amikor a központi
test nem pontszerű. Kimutatta, hogy az a gömb alakú
test, amelynek tömegeloszlása gömbszimmetriát mutat, a
vonzás szempontjából úgy viselkedik, mintha egész tömege
a gömb középpontjában lenne összesűrítve.
Hooke és Newton állította, hogy mindenégitest vonzást
fejt ki saját középpontja irányában, így gravitációs
kapcsolatra (kölcsönhatásra) alkalmas. A Nap hat a bolygóra,
de a bolygó is hat a Napra. Tehát a pontszerűnek
tekinthető 1-es és 2-es jelzésű tárgyak esetében két erővel
kell számolni, amelyek abszolút értéke egyenesen
arányos a két test tömegének szorzatával, és fordítva arányos
a köztük levő távolság négyzetével. Az 1-es tárgynak
2-esre gyakorolt gravitációs hatását az
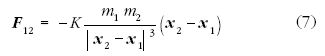
erő segítségével írjuk le, amelyben K gravitációs állandót,
m1 és m2 tömegeket, x1 és
x2 helyzetvektorokat jelöl. A
2-es tárgynak az 1-esre gyakorolt hatását kifejező F21 erő
F12-től előjelben különbözik. Az origóban rögzített M
tömegű, pontszerű tárgynak a tőle r távolságban levő, m
tömegű tárgyra gyakorolt gravitációs hatását az
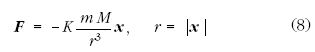
erőképlet segítségével írjuk le.
A gravitáció kérdését szívén viselő Hooke 1680-ban
Newtont továbblépésre ösztönözte. A megoldásra váró
feladatok körébe sorolta annak a bizonyítását, hogy a (8)
alatti erőképletet felhasználva ellipszis alakú bolygópályához
jutunk. Newton, a differenciálszámítás egyik úttörője,
ezt a feladatot is sikerrel oldotta meg.
Newton a pontszerű testek esetében elsőként létesített
kapcsolatot a testre ható erő és a test gyorsulása között:

A bal oldalon szereplő m mennyiséget ma tehetetlen
tömegnek nevezzük, és állítjuk, hogy e mennyiség azt az
ellenállást méri, amelyet a test sebessége megváltoztatásakor
tanúsít. Newton hallgatólagosan feltételezte, hogy a
súlyos és tehetetlentömeg értéke egyezik. Ezt elfogadva
(8) és (9) alapján

írható. E mozgásegyenlet alapján valóban ellipszis alakú
bolygópályákhoz jutunk. Fontos tényként állapíthatjuk
meg, hogy (10)-ben m nem szerepel. Tehát ha egy adott
pillanatban a bolygót egy fémgolyóval cserélnénk fel, a
golyó a bolygópályán folytatná útját.
A bolygók mozgásának vizsgálata vezetett a (7) alatti
erőtörvényhez. A törvény érvényességét Newton a Világegyetem
egészére is kiterjesztette. Ezért beszélünk egyetemes
gravitációs törvényről. Newton után már nem lehetett
égi és földi fizikáról beszélni.
A newtoni alap bővítése, új utak keresése
Egy elmélet létjogát a gyakorlat igazolja. A newtoni tömegvonzási
elmélet sikerrel vizsgázott. H. Cavendish
1798-ban földi körülmények között is bizonyította (súlyos
ólomgolyók felhasználásával) a gravitációs törvény
érvényességét. Eötvös Loránd 1909-ben igazolta, hogy a
súlyos és tehetetlentömeg egyenlősége 10-8 relatív mérési
hiba határán belül fennáll. Számításba vettek olyan
hatásokat, amelyeket korábban figyelmen kívül hagytak,
például a bolygómozgás esetében a többi bolygó zavaró
hatását. E törekvés legnagyobb eredménye az volt, hogy
az Uránusz bolygó mozgásában mutatkozó rendellenességeket
magyarázva, megtalálták a zavaró tényezőt, az
1846-ban felfedezett Neptunusz bolygót.
A fizika eszköztára folyamatosan bővül. A newtoni
mechanika és gravitációelmélet a gazdagításhoz szilárd,
megbízható alapot nyújtott. A tényeket magyarázó, a
tényanyag rendszerezését szolgáló elmélet hasznosítása
során egyre jobban kirajzolódik az elmélet alkalmazhatósági
területe. A nagy sebességgel végbemenő mozgások
vizsgálata új elméletet igényelt. A newtoni gravitációs
törvénnyel kapcsolatban is problémák jelentkeztek.
Ezek közül csak kettőt emelünk ki. A bolygópályák
rozetta alakúak (az ellipszispálya elforog). A pálya Naphoz
legközelebbi pontja (perihéliuma) igen lassan körbevándorol.
A perihélium-elmozdulás egy része a többi
bolygó hatásával magyarázható, egy másik része azonban
newtoni magyarázat nélkül maradt. Ezt elsőként Le
Verrier jelezte 1859-ben, a Merkúr bolygó esetében.
Eredményét 1898-ban S. Newcomb megerősítette, és a
magyarázatra váró változásra a ma is használt 43 ívmásodperc/
évszázad értéket adta. Newton gravitációs törvényének
érvényességét a Világegyetem egészére is
kiterjesztette. De ekkor a térben végtelen Világegyetem
esetében egyes fizikai mennyiségek végtelenekké válnak.
A végtelentől irtózó fizikus és csillagász ezt nem
fogadhatta el. Nyilvánvalóvá vált, hogy a gravitáció
newtoni magyarázat nélkül maradt kérdései a newtoni
keret túllépését igénylik.
A következőkben azokból a próbálkozásokból válogatunk,
amelyek a gravitációelmélet terén való előrehaladást
célozták.
J.L. Lagrange 1788-ban közzétett Mécanique analytique
című munkájában összegezte a ma nevét viselő új
mechanikájának eredményeit. A gravitáció elméletét
1773-ban a gravitációs potenciálfüggvénnyel gazdagította.
A gravitációs hatásnak kitett m tömegű testre ható erőt
a  potenciálfüggvényt tartalmazó
potenciálfüggvényt tartalmazó

kapcsolat adja.
S. Poisson 1813-ban  -re a
-re a
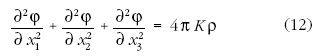
differenciálegyenletet adta, amelyben 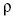 tömegsűrűséget
jelöl. Amennyiben az origóban rögzített M tömegű, pontszerű
tárgy hatásával kell számolnunk, (12) jobb oldalán
tömegsűrűséget
jelöl. Amennyiben az origóban rögzített M tömegű, pontszerű
tárgy hatásával kell számolnunk, (12) jobb oldalán
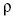 helyett
az
helyett
az 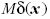 kifejezést írjuk, amelyben
a
kifejezést írjuk, amelyben
a 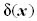 Dirac-féle disztribúció szerepel. Ameddig ezt a matematikai
objektumot nem ismerték, (12) jobb oldalára zérót
írtak azzal a megjegyzéssel, hogy az így nyert Laplace egyenlet
az origón kívüli tartományban használható.
A (8) alatti erő a
Dirac-féle disztribúció szerepel. Ameddig ezt a matematikai
objektumot nem ismerték, (12) jobb oldalára zérót
írtak azzal a megjegyzéssel, hogy az így nyert Laplace egyenlet
az origón kívüli tartományban használható.
A (8) alatti erő a

potenciálból származtatható, amelyik az origón kívül
teljesíti a
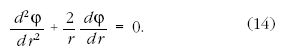
egyenletet.
Az előbbiekben a gravitációelmélet eszköztárát a 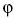 függvénnyel bővítettük, de nem léptünk ki a newtoni
keretből. Ezt C. Neumann tette meg azzal, hogy 1873-ban
(14) bal oldalát a
függvénnyel bővítettük, de nem léptünk ki a newtoni
keretből. Ezt C. Neumann tette meg azzal, hogy 1873-ban
(14) bal oldalát a 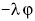 taggal egészítette ki
(
taggal egészítette ki
(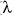 állandó).
Ily módon a
állandó).
Ily módon a
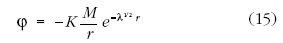
potenciálhoz jutott.
A Poisson-egyenlet és a Neumann-féle "világállandó"
fontos szerephez jutott a gravitáció későbbi történetében.
A (15) alatti potenciál kiküszöbölte a "gravitációs paradoxon"-t
(a Világegyetem egészére véges értékeket szolgáltatott),
de alkalmatlannak bizonyult arra, hogy a Naprendszer
valamennyi bolygójára helyes perihélium elmozdulás-
értéket nyújtson.
Ch.A. Coulomb 1785-ben kimutatta, hogy az elektromos
töltéssel rendelkező, pontszerű tárgyak esetében
egy olyan erőtörvény használható, amelyik a newtoni
gravitációs törvényre emlékeztet. W. Weber 1846-ban
arra a következtetésre jutott, hogy a mozgó töltések kölcsönhatásának
leírásakor a töltést hordozó tárgyak sebességét
is figyelembe kell venni. Arra is felhívta a figyelmet,
hogy eredményeit a gravitáció elméletében is
hasznosítani lehetne.
Tekintsük a Nap-bolygó rendszert. A Weber-féle
program hívei ebben az esetben Lagrange-keretbe illő (a
bolygó helyét és sebességét rögzítő adatoktól függő) potenciálokkal
próbálkoztak. A javasolt függvények közül a
Gerber-féle, 1898-ban közölt
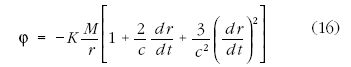
potenciál vált közismertté. E potenciál a perihélium-
elmozdulásra a ma is használt, helyes
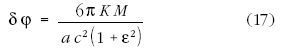
kifejezést adta, amelyben a a fél nagytengely hosszát, c a
fény vákuumbeli terjedési sebességét, 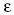 a bolygópálya
numerikus excentricitását jelöli. A (17) által adott
a bolygópálya
numerikus excentricitását jelöli. A (17) által adott 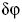 szög
egy keringésre vonatkozik. P. Gerber potenciáljára nem
tudott elfogadható indoklást adni, úgy tűnik, hogy potenciálját
a Newcomb által röviddel korábban (egyazon évben)
nyert, a fentiekben már említett adathoz igazította.
Az elektromágneses kölcsönhatás eredményeinek a
gravitáció elméletébe történő átültetése zsákutcának bizonyult.
Ennek ellenére ez az eljárás legalább két szempontból
hasznot hozott. A (17) alatti képlet a gravitáció
elméletében ugyanazt a szerepet töltötte be, mint a Balmer-
képlet a kvantumelméletben. Másrészt, a potenciálfüggvényekben
szerepeltetett c sebesség azt sugallta,
hogy a gravitációs hatás véges sebességgel terjed.
A helyes útra léptek azok, akik a harmadik utat választották.
Ezen az úton az első lépéseket a két Bolyai
és N.I. Lobacsevszkij tették meg. A newtoni elmélet az
euklideszi geometriára alapoz. Miután Bolyai János és
Lobacsevszkij az euklideszi geometria egyeduralmát
megtörték, egy új, nemeuklideszi alapot kínáltak.
Bolyai Farkas 1832-ben kiadott Tentamen című munkája
első kötetében egy zseniális sejtést fogalmazott
meg. Elsőként állította, hogy a bolygók mozgásában
jelentkezhetnek olyan zavarok, amelyeket csak nemeuklideszi
alapon lehet magyarázni. A sejtést a fejlődés
27 év múltán a tények körébe sorolta.
Bolyai János továbblépett. Egy 1835-ös keltezésű kéziratában
a nemeuklideszi alapra helyezett mechanika
kidolgozását szorgalmazta. Első lépésként egy új, nemnewtoni
gravitációs törvényt adott. Az M tömegű test által,
tőle r távolságban lévő, m tömegű testre gyakorolt
centrális erő radiális komponensére a newtoni elmélet az
szög
egy keringésre vonatkozik. P. Gerber potenciáljára nem
tudott elfogadható indoklást adni, úgy tűnik, hogy potenciálját
a Newcomb által röviddel korábban (egyazon évben)
nyert, a fentiekben már említett adathoz igazította.
Az elektromágneses kölcsönhatás eredményeinek a
gravitáció elméletébe történő átültetése zsákutcának bizonyult.
Ennek ellenére ez az eljárás legalább két szempontból
hasznot hozott. A (17) alatti képlet a gravitáció
elméletében ugyanazt a szerepet töltötte be, mint a Balmer-
képlet a kvantumelméletben. Másrészt, a potenciálfüggvényekben
szerepeltetett c sebesség azt sugallta,
hogy a gravitációs hatás véges sebességgel terjed.
A helyes útra léptek azok, akik a harmadik utat választották.
Ezen az úton az első lépéseket a két Bolyai
és N.I. Lobacsevszkij tették meg. A newtoni elmélet az
euklideszi geometriára alapoz. Miután Bolyai János és
Lobacsevszkij az euklideszi geometria egyeduralmát
megtörték, egy új, nemeuklideszi alapot kínáltak.
Bolyai Farkas 1832-ben kiadott Tentamen című munkája
első kötetében egy zseniális sejtést fogalmazott
meg. Elsőként állította, hogy a bolygók mozgásában
jelentkezhetnek olyan zavarok, amelyeket csak nemeuklideszi
alapon lehet magyarázni. A sejtést a fejlődés
27 év múltán a tények körébe sorolta.
Bolyai János továbblépett. Egy 1835-ös keltezésű kéziratában
a nemeuklideszi alapra helyezett mechanika
kidolgozását szorgalmazta. Első lépésként egy új, nemnewtoni
gravitációs törvényt adott. Az M tömegű test által,
tőle r távolságban lévő, m tömegű testre gyakorolt
centrális erő radiális komponensére a newtoni elmélet az
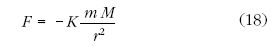
képletet adta. A (18) jobb oldalán szereplő törtet 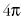 -vel
bővítve a nevezőben, a gömbfelszínre érvényes euklideszi
kifejezés jelentkezik. A Bolyai-Lobacsevszkij-geometria
a gömbfelszínre a
-vel
bővítve a nevezőben, a gömbfelszínre érvényes euklideszi
kifejezés jelentkezik. A Bolyai-Lobacsevszkij-geometria
a gömbfelszínre a

kifejezést adta. Bolyai erre alapozott, amikor (18)-at az
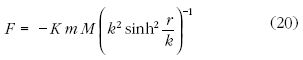
erőképlettel helyettesítette. Bolyai világában k-nak a
természetes hosszegység szerepet szánta, és a valóságnak
megfelelő k érték megadását a megoldandó feladatok
körébe sorolta.
Bolyai János erőtörvényével fél évszázaddal előzte
meg korát. P. Stäckel, aki még láthatta a törvényt tartalmazó
kéziratot, az 1903-ban közölt A többméretű sokaságok
mechanikájáról című dolgozatában a következőket
írta: "Érdekes, hogy egy bolygó mozgását a központi test
körül Killing (1885-ben) ugyancsak a Bolyai Jánostól
föltételezett vonzási törvény mellett discutálta." Később
Stäckel 1914-ben kiadott Bolyai Farkas és Bolyai János
geometriai vizsgálatai című könyvében azt is jelezte,
hogy Lobacsevszkij Bolyaival csaknem egy időben szintén megállapította
a (20) alatti törvényt, amelyet a Kazáni
Egyetem Tudományos Közleményeiben közölt. Ezért
(20)-at joggal nevezhetjük Bolyai-Lobacsevszkij-féle
gravitációs törvények.
Nem véletlen, hogy Bolyai és Lobacsevszkij elképzelései
az ő idejükben nem tudtak gyökeret verni. Geometriájukat
csak 1860 után ismerték el, így gravitációs törvényük
sem számíthatott elismerésre.
B. Riemann 1854-ben tartotta meg a göttingeni egyetemen
A geometria alapjait képezo feltevések című habilitációs
előadását. (Dolgozata csak halála után, 1867-ben
látott napvilágot.) Ezzel a nemeuklideszi geometria történetében
új korszak kezdődött. Bolyai-Lobacsevszkij-geometria
elszigeteltsége megszűnt, az új nemeuklideszi geometria
eszköz- és fogalomtára folyamatosam gazdagodott.
Fontos szerephez jutott a görbület fogalma. A Bolyai-
Lobacsevszkij-féle világot az állandó, negatív görbületű
(hiperbolikus) terek körébe sorolták.
A riemanni geometria fontos szerepet játszott az Einstein-
féle modern gravitációelmélet megalapozásában. Az
általunk szemügyre vett korszakban a fizikusok és csillagászok
az állandó görbületű terek használatára szorítkoztak.
A Nap-bolygó rendszer vizsgálata ismét napirendre került.
A bolygómozgást állandó görbületű terekben R. Lipschitz
(1873), A. Cayley (1873), W. Killing (1885) vizsgálták.
Térjünk vissza a (20) alatti törvényhez. Első pillanatban
úgy tűnik, hogy az általánosítással nyert törvény
minden elvi alapot nélkülöz. Ez nem így van. Az erő a
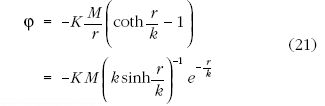
potenciálból származtatható.
Az 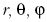 gömbi koordináták segítségével megadott
gömbi koordináták segítségével megadott
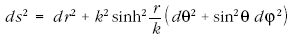
Ívelem négyzet kifejezés felhasználásával a (14) egyenlet
hiperbolikus megfelelőjéhez jutunk:
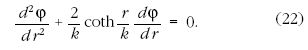
A Bolyai-Lobacsevszkij-féle potenciál teljesíti a (22)
egyenletet. (20)-ból a 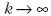 esetben a newtoni kifejezéshez
jutunk. Mivel ksinh (r/k) > r, (20) alapján
esetben a newtoni kifejezéshez
jutunk. Mivel ksinh (r/k) > r, (20) alapján
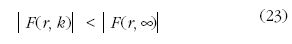
írható, tehát a hiperbolikus esetben a newtoni vonzást
árnyékoló (gyengítő) hatással kell számolni.
Bolyai új világának szerkezetét a k értéke szabja meg,
az a k érték, amelyik a gravitációs törvényben is szerepel.
Lehet, hogy Bolyai János erre gondolt, amikor a gravitáció
és a tér szerkezete közötti kapcsolatot állító sorait
megfogalmazta:
"A nehézkedés törvénye is szoros összveköttetésben,
foljtatásban tetszik [mutatkozik] az űr termetével, valójával
[alkatával] miljségével s [gondolom] az egész természet
[világ] foljásával."
Bolyai nem tudott a Gauss által 1828-ban bevezetett
görbületfogalomról és arról, hogy új világának a görbületét
a k értéke szabja meg. Ma már állítjuk, hogy Bolyai a
háromdimenziós euklideszi teret meggörbítette a gravitáció
segítségével, miáltal a newtoni gravitációs törvény
helyébe egy új törvényt állított.
Bolyai nem lépett ki a klasszikus keretből, erre az ő
idejében nem volt lehetőség. A továbblépést 1905, a speciális
relativitáselmélet megalapozásai után lehetett megtenni.
Az új elmélet egy pszeudo-euklideszi szerkezetű
négydimenziós téridőt kínált, és ezzel a gravitációelmélet
alkalmassá vált a riemanni geometria befogadására. A
négydimenziós téridő meggörbítésére Einstein vállalkozott,
és ezzel a gravitációt teljesen új megvilágításba helyezte.
Például a Nap által meggörbített pszeudo-riemanni
térből száműzte a gravitációs erőt és a téridőben a
bolygók számára szabad utat biztosított.




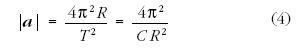
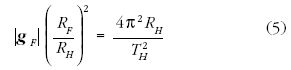

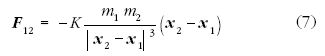
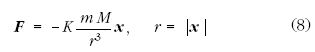


 potenciálfüggvényt tartalmazó
potenciálfüggvényt tartalmazó

 -re a
-re a
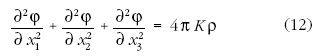
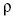 tömegsűrűséget
jelöl. Amennyiben az origóban rögzített M tömegű, pontszerű
tárgy hatásával kell számolnunk, (12) jobb oldalán
tömegsűrűséget
jelöl. Amennyiben az origóban rögzített M tömegű, pontszerű
tárgy hatásával kell számolnunk, (12) jobb oldalán
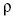 helyett
az
helyett
az 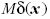 kifejezést írjuk, amelyben
a
kifejezést írjuk, amelyben
a 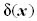 Dirac-féle disztribúció szerepel. Ameddig ezt a matematikai
objektumot nem ismerték, (12) jobb oldalára zérót
írtak azzal a megjegyzéssel, hogy az így nyert Laplace egyenlet
az origón kívüli tartományban használható.
A (8) alatti erő a
Dirac-féle disztribúció szerepel. Ameddig ezt a matematikai
objektumot nem ismerték, (12) jobb oldalára zérót
írtak azzal a megjegyzéssel, hogy az így nyert Laplace egyenlet
az origón kívüli tartományban használható.
A (8) alatti erő a

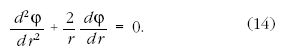
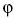 függvénnyel bővítettük, de nem léptünk ki a newtoni
keretből. Ezt C. Neumann tette meg azzal, hogy 1873-ban
(14) bal oldalát a
függvénnyel bővítettük, de nem léptünk ki a newtoni
keretből. Ezt C. Neumann tette meg azzal, hogy 1873-ban
(14) bal oldalát a 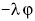 taggal egészítette ki
(
taggal egészítette ki
(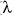 állandó).
Ily módon a
állandó).
Ily módon a
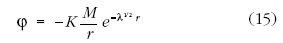
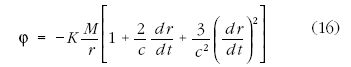
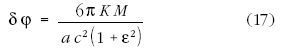
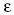 a bolygópálya
numerikus excentricitását jelöli. A (17) által adott
a bolygópálya
numerikus excentricitását jelöli. A (17) által adott 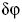 szög
egy keringésre vonatkozik. P. Gerber potenciáljára nem
tudott elfogadható indoklást adni, úgy tűnik, hogy potenciálját
a Newcomb által röviddel korábban (egyazon évben)
nyert, a fentiekben már említett adathoz igazította.
Az elektromágneses kölcsönhatás eredményeinek a
gravitáció elméletébe történő átültetése zsákutcának bizonyult.
Ennek ellenére ez az eljárás legalább két szempontból
hasznot hozott. A (17) alatti képlet a gravitáció
elméletében ugyanazt a szerepet töltötte be, mint a Balmer-
képlet a kvantumelméletben. Másrészt, a potenciálfüggvényekben
szerepeltetett c sebesség azt sugallta,
hogy a gravitációs hatás véges sebességgel terjed.
A helyes útra léptek azok, akik a harmadik utat választották.
Ezen az úton az első lépéseket a két Bolyai
és N.I. Lobacsevszkij tették meg. A newtoni elmélet az
euklideszi geometriára alapoz. Miután Bolyai János és
Lobacsevszkij az euklideszi geometria egyeduralmát
megtörték, egy új, nemeuklideszi alapot kínáltak.
Bolyai Farkas 1832-ben kiadott Tentamen című munkája
első kötetében egy zseniális sejtést fogalmazott
meg. Elsőként állította, hogy a bolygók mozgásában
jelentkezhetnek olyan zavarok, amelyeket csak nemeuklideszi
alapon lehet magyarázni. A sejtést a fejlődés
27 év múltán a tények körébe sorolta.
Bolyai János továbblépett. Egy 1835-ös keltezésű kéziratában
a nemeuklideszi alapra helyezett mechanika
kidolgozását szorgalmazta. Első lépésként egy új, nemnewtoni
gravitációs törvényt adott. Az M tömegű test által,
tőle r távolságban lévő, m tömegű testre gyakorolt
centrális erő radiális komponensére a newtoni elmélet az
szög
egy keringésre vonatkozik. P. Gerber potenciáljára nem
tudott elfogadható indoklást adni, úgy tűnik, hogy potenciálját
a Newcomb által röviddel korábban (egyazon évben)
nyert, a fentiekben már említett adathoz igazította.
Az elektromágneses kölcsönhatás eredményeinek a
gravitáció elméletébe történő átültetése zsákutcának bizonyult.
Ennek ellenére ez az eljárás legalább két szempontból
hasznot hozott. A (17) alatti képlet a gravitáció
elméletében ugyanazt a szerepet töltötte be, mint a Balmer-
képlet a kvantumelméletben. Másrészt, a potenciálfüggvényekben
szerepeltetett c sebesség azt sugallta,
hogy a gravitációs hatás véges sebességgel terjed.
A helyes útra léptek azok, akik a harmadik utat választották.
Ezen az úton az első lépéseket a két Bolyai
és N.I. Lobacsevszkij tették meg. A newtoni elmélet az
euklideszi geometriára alapoz. Miután Bolyai János és
Lobacsevszkij az euklideszi geometria egyeduralmát
megtörték, egy új, nemeuklideszi alapot kínáltak.
Bolyai Farkas 1832-ben kiadott Tentamen című munkája
első kötetében egy zseniális sejtést fogalmazott
meg. Elsőként állította, hogy a bolygók mozgásában
jelentkezhetnek olyan zavarok, amelyeket csak nemeuklideszi
alapon lehet magyarázni. A sejtést a fejlődés
27 év múltán a tények körébe sorolta.
Bolyai János továbblépett. Egy 1835-ös keltezésű kéziratában
a nemeuklideszi alapra helyezett mechanika
kidolgozását szorgalmazta. Első lépésként egy új, nemnewtoni
gravitációs törvényt adott. Az M tömegű test által,
tőle r távolságban lévő, m tömegű testre gyakorolt
centrális erő radiális komponensére a newtoni elmélet az
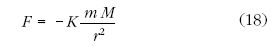
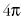 -vel
bővítve a nevezőben, a gömbfelszínre érvényes euklideszi
kifejezés jelentkezik. A Bolyai-Lobacsevszkij-geometria
a gömbfelszínre a
-vel
bővítve a nevezőben, a gömbfelszínre érvényes euklideszi
kifejezés jelentkezik. A Bolyai-Lobacsevszkij-geometria
a gömbfelszínre a

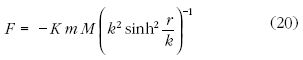
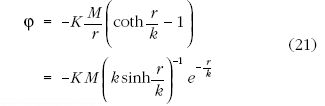
 gömbi koordináták segítségével megadott
gömbi koordináták segítségével megadott
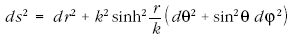
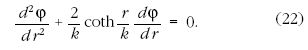
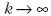 esetben a newtoni kifejezéshez
jutunk. Mivel ksinh (r/k) > r, (20) alapján
esetben a newtoni kifejezéshez
jutunk. Mivel ksinh (r/k) > r, (20) alapján