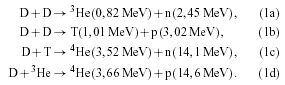
Fizikai Szemle honlap |
Tartalomjegyzék |
Zoletnik Sándor
KFKI Részecske- és Magfizikai Kutató Intézet,
Magyar EURATOM Fúziós Szövetség
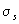 a Coulomb-szórás hatáskeresztmetszete
és
a Coulomb-szórás hatáskeresztmetszete
és 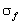 a fúziós
reakció hatáskeresztmetszete. Tegyük fel, hogy a nyaláb
teljesen elnyelődik a céltárgyban, valamint ha egy részecskéje
Coulomb-szórást szenved, akkor nem képes már
fuzionálni, és energiáját a további ütközésekben teljesen leadja.
A fenti esetben a céltárgyból kijövő
teljesítmény:
ahol Ef az egy fúziós reakcióban keletkező
energia. A fúziós
reakciók küszöbenergiája tipikusan 10 keV, a felszabaduló
fúziós energia pedig nagyságrendileg Ef = 10 MeV,
tehát Ef / Eb körülbelül 103.
Sajnos
a fúziós
reakció hatáskeresztmetszete. Tegyük fel, hogy a nyaláb
teljesen elnyelődik a céltárgyban, valamint ha egy részecskéje
Coulomb-szórást szenved, akkor nem képes már
fuzionálni, és energiáját a további ütközésekben teljesen leadja.
A fenti esetben a céltárgyból kijövő
teljesítmény:
ahol Ef az egy fúziós reakcióban keletkező
energia. A fúziós
reakciók küszöbenergiája tipikusan 10 keV, a felszabaduló
fúziós energia pedig nagyságrendileg Ef = 10 MeV,
tehát Ef / Eb körülbelül 103.
Sajnos 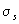 /
/ 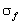 tipikusan 10-5
nagyságrendben van, így Pt = 1,01Pb. Mivel a nyaláb
gyorsításához a Pt teljesítményt csak tipikusan 30% körüli
hatásfokkal tudjuk átalakítani a Pb nyalábteljesítménnyé,
ezért nyilvánvaló, hogy ilyen módon nem lehet pozitív
energiamérleget elérni.
Gyökeresen más a helyzet, ha termikus közegben szeretnénk
fúziós energiát termelni. Ilyenkor a Coulombszórás
csak elosztja az energiát a részecskék között és nem
jelent veszteséget. Természetesen ekkor viszont a hőmérsékletnek
olyan magasnak lenni, hogy a részecskék jelentős része 10 keV körüli
energiával rendelkezzen. Ez nagyságrendileg
100 millió K hőmérsékleten következik be, tehát
ilyen hőmérsékletű deutérium-trícium közegben tudnánk
fúziós energiát termelni.
Vizsgáljuk most meg, hogy milyen feltételek mellett
kapunk pozitív energiamérleget egy termikus közegből.
Vegyünk egy V térfogatú, n sűrűségű, 50-50%-os
deutérium-tríciumösszetételű homogén közeget. A felszabaduló
fúziós teljesítményt a termikus sebességeloszlásra
kiátlagolt C(T) = (
tipikusan 10-5
nagyságrendben van, így Pt = 1,01Pb. Mivel a nyaláb
gyorsításához a Pt teljesítményt csak tipikusan 30% körüli
hatásfokkal tudjuk átalakítani a Pb nyalábteljesítménnyé,
ezért nyilvánvaló, hogy ilyen módon nem lehet pozitív
energiamérleget elérni.
Gyökeresen más a helyzet, ha termikus közegben szeretnénk
fúziós energiát termelni. Ilyenkor a Coulombszórás
csak elosztja az energiát a részecskék között és nem
jelent veszteséget. Természetesen ekkor viszont a hőmérsékletnek
olyan magasnak lenni, hogy a részecskék jelentős része 10 keV körüli
energiával rendelkezzen. Ez nagyságrendileg
100 millió K hőmérsékleten következik be, tehát
ilyen hőmérsékletű deutérium-trícium közegben tudnánk
fúziós energiát termelni.
Vizsgáljuk most meg, hogy milyen feltételek mellett
kapunk pozitív energiamérleget egy termikus közegből.
Vegyünk egy V térfogatú, n sűrűségű, 50-50%-os
deutérium-tríciumösszetételű homogén közeget. A felszabaduló
fúziós teljesítményt a termikus sebességeloszlásra
kiátlagolt C(T) = (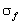 v) reakciórátával a következőképpen
írhatjuk fel:
A közeg hőveszteségét egyetlen mennyiséggel, az ún.
energia-összetartási idővel (
v) reakciórátával a következőképpen
írhatjuk fel:
A közeg hőveszteségét egyetlen mennyiséggel, az ún.
energia-összetartási idővel (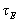 ) jellemezzük:
ahol Wtot a teljes termikus energiatartalom. Az energiaösszetartási
idő tehát azt mondja meg, hogy a közeg milyen
ütemben veszít energiát, jól szigetelt állapotban az energiaösszetartási
idő nagy. Adott Q = Pf / Pv energiasokszorozási
tényező elérésének feltételére a (4) és (5) képletből a
következő kritériumra jutunk:
Az egyenlőtlenség jobb oldalát a D-T reakció optimális
hőmérsékletére kiértékelve Q = 1 esetén kapjuk a nevezetes Lawson-kritériumot:
A Lawson-kritérium kielégítése természetesen nem elég
még energiatermeléshez, ehhez legalább Q = 10 körüli értékek
szükségesek. Meg kell jegyezni, hogy az optimum
közelében a C(T) függvény parabolával közelíthető, így a
különböző berendezések összehasonlítására az n
) jellemezzük:
ahol Wtot a teljes termikus energiatartalom. Az energiaösszetartási
idő tehát azt mondja meg, hogy a közeg milyen
ütemben veszít energiát, jól szigetelt állapotban az energiaösszetartási
idő nagy. Adott Q = Pf / Pv energiasokszorozási
tényező elérésének feltételére a (4) és (5) képletből a
következő kritériumra jutunk:
Az egyenlőtlenség jobb oldalát a D-T reakció optimális
hőmérsékletére kiértékelve Q = 1 esetén kapjuk a nevezetes Lawson-kritériumot:
A Lawson-kritérium kielégítése természetesen nem elég
még energiatermeléshez, ehhez legalább Q = 10 körüli értékek
szükségesek. Meg kell jegyezni, hogy az optimum
közelében a C(T) függvény parabolával közelíthető, így a
különböző berendezések összehasonlítására az n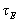 T, ún.
fúziós hármas szorzatot szokás használni (feltéve, hogy a
hőmérséklet eléri a 10 keV nagyságrendet).
A reaktorműködés megértéséhez vizsgáljuk meg, mi
történik egy ilyen forró közeggel, amikor az eléri ésmeghaladja
a Lawson-kritériumot! Az (1c) folyamatból láthatjuk,
hogy a D-T reakcióban felszabaduló energia kb. 20%-át az
T, ún.
fúziós hármas szorzatot szokás használni (feltéve, hogy a
hőmérséklet eléri a 10 keV nagyságrendet).
A reaktorműködés megértéséhez vizsgáljuk meg, mi
történik egy ilyen forró közeggel, amikor az eléri ésmeghaladja
a Lawson-kritériumot! Az (1c) folyamatból láthatjuk,
hogy a D-T reakcióban felszabaduló energia kb. 20%-át az
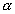 -részecske viszi el. Ez töltött, így viszonylag nagy hatáskeresztmetszettel
ütközik a D-T magokkal, és kedvező körülmények
között leadja energiáját a közegben, így képes a
hőveszteséget pótolni (
-részecske viszi el. Ez töltött, így viszonylag nagy hatáskeresztmetszettel
ütközik a D-T magokkal, és kedvező körülmények
között leadja energiáját a közegben, így képes a
hőveszteséget pótolni (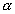 -fűtés). A 2. ábra vázlatosan mutatja,
mi történik a közeg melegítésekor. A folytonos vonal
az
-fűtés). A 2. ábra vázlatosan mutatja,
mi történik a közeg melegítésekor. A folytonos vonal
az 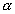 -fűtés teljesítményét mutatja, amely a hőmérséklet
emelésével egy darabig nő, majd az optimális hőmérséklet
elérése után csökkenni kezd. A veszteségek (szaggatott
vonal) viszont mindenképpen monoton (sőt, a lineárisnál
gyorsabban) növekednek. A két görbének nincs metszéspontja,
ha a veszteségek túl nagyok. Bizonyos veszteségi
szint alatt viszont két metszéspont jelenik meg. Amikor a
közeget fűtjük, először a bal oldali pontot érjük el, amely
instabil (a hőmérséklet kis emelkedésére teljesítménytöbblet
jelentkezik). Ebből a pontból tehát a berendezés át fog
ugrani egészen a jobb oldali pontig, amely stabil. További
melegedés, megszaladás alapvető fizikai folyamatok miatt
nem lehetséges, és a veszteségi teljesítményt az
-fűtés teljesítményét mutatja, amely a hőmérséklet
emelésével egy darabig nő, majd az optimális hőmérséklet
elérése után csökkenni kezd. A veszteségek (szaggatott
vonal) viszont mindenképpen monoton (sőt, a lineárisnál
gyorsabban) növekednek. A két görbének nincs metszéspontja,
ha a veszteségek túl nagyok. Bizonyos veszteségi
szint alatt viszont két metszéspont jelenik meg. Amikor a
közeget fűtjük, először a bal oldali pontot érjük el, amely
instabil (a hőmérséklet kis emelkedésére teljesítménytöbblet
jelentkezik). Ebből a pontból tehát a berendezés át fog
ugrani egészen a jobb oldali pontig, amely stabil. További
melegedés, megszaladás alapvető fizikai folyamatok miatt
nem lehetséges, és a veszteségi teljesítményt az 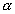 -fűtés teljesen
fedezi (Q =
-fűtés teljesen
fedezi (Q = 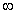 ). Ebben az állapotban tehát a fúziós
erőmű folyamatosan működni tudna, csak az energiájukat
leadott He-magok kiszívásáról és friss D-T keverék bejuttatásáról
kell gondoskodni. Ezt az állapotot fúziós égésnek
nevezzük. Meg kell jegyezni, hogy ebben az állapotban
kevés lehetőség van a berendezés vezérlésére, ezért a kísérletek
inkább a Q = 10-30 közötti paramétertartományt
veszik célba.
A kezdetek
A Lawson-kritérium kielégítésére két úton lehet elindulni:
jó szigetelés (hosszú energia-összetartási idő) és alacsony
sűrűség, vagy igen magas sűrűségmellett rövid összetartás,
vagyis robbanás. Ez utóbbi megoldást inerciális összetartásnak
szokás nevezni, mivel egy r sugarú gömb körülbelül
r/cs ideig mindenképpen egyben marad (ahol cs a közegbeli
hangsebesség). A Lawson-kritérium állandó állapotot
tételez fel, így az inerciális fúzió esetére nem érvényes,
mégis az erre vonatkozó megfontolások arra vezetnek,
hogy a megvalósításhoz a szilárdtest-sűrűség körülbelül
ezerszeresét kell elérni. Ezt a sűrűséget kisméretű kapszulák
lézeres, röntgensugárzásos vagy részecskenyalábos
összenyomásával próbálják elérni. Ennek során olyan extrém
állapotba kell vinni az anyagot, ami a Földön leginkább
nukleáris robbantások alkalmával jön létre, így nem
csoda, hogy az inerciális fúziós kutatások sok ponton kapcsolódnak
katonai fejlesztésekhez, és így nem teljesen nyilvánosak.
Lézeres fúziós célra jelenleg két nagy berendezés
is épül (NIF, USA és LMJ, Franciaország), és ezek a tervek
szerint egy-egy kapszulából pozitív energiamérleget is
fognak elérni [2]. Ennek ellenére ilyen alapú reaktor
megépítése
távolinak tűnik. Az inerciális fúziós kutatások önmagukban
is egy külön cikket igényelnének, ezért velük itt
a továbbiakban nem foglalkozunk.
A nagyságrendileg 10 keV (100 millió °C) hőmérsékletű fúziós közegre hosszú
energia-összetartási időt tűzve ki célul kihasználhatjuk, hogy ezen a
hőmérsékleten az anyag mindenképpen plazmaállapotban van, azaz az elektronok
leszakadnak az atommagokról. A plazma elektromágnesesen kölcsönható közeg,
így összetartásához megpróbálkozhatunk mágneses terekkel. Ilyen kutatások az
1950-es évek elején nagy titoktartás mellett indultak meg elsősorban az
USA-ban, Angliában és a Szovjetúnióban. Az évtized végére világossá vált,
hogy nem lehet gyors eredményt elérni, ilyen extrém állapotú anyagok
viselkedésének megértéséhez még alapkutatásokra is szükség van. Az
eredményeket fokozatosan nyilvánossá tették, 1
a kutatások ma már évtizedek óta széles nemzetközi együttműködésben folynak.
Mágneses plazmaösszetartás
Mágneses térben a plazma töltött részecskéi (az elektronok
és az ionok) a mágneses erővonalak körül Larmor-pályán
mozognak, ahogy azt a 3. ábra mutatja. A Larmor-pálya
sugara erős mágneses térben (kb. 1 T) még a 10 keV-es
deutérium és trícium atommagokra sem nagyobb, mint néhány
milliméter. A térre merőleges irányban a részecskék
gyakorlatilag nem tudnak elmozdulni, és mintegy csőbe
zárható a plazma. A csővégeinek "bedugaszolását"
először mágneses tükrökkel próbálták megoldani. Ezekben a
mágneses tér erőssége az erővonalak mentén növekszik. A
Larmor-pályán mozgó részecskék köráramot és ezzel
mágneses dipólust képviselnek. Erre a mágneses tér gradiense
erőt fejt ki, akárcsak egy mágnesre. Ennek eredményeképpen
a részecskék visszaverődnek a nagyobb terű tartományoktól.
Sajnos a visszatérítő erő a mágneses térhez képest kis
szögben hajló pályán futó részecskékre nem elég nagy, így
két mágneses tükör közötti tartományban a részecskéknek
csak egy része tartható össze. Az ütközések miatt az összetartott
részecskék is egy idő után olyan irányú sebességet
kaphatnak, amellyel kijutnak a berendezésből. Ezeknek
a problémáknak a kiküszöbölésére különböző elektrosztatikus
csapdák hozzáadásával kísérleteztek, de az eredmények
nem voltak túl biztatóak, így az ilyen lineáris berendezésekkel
folyó kísérleteket a 80-as évek tájékán nagyrészt feladták.
A mágneses teret tórusz alakú zárt erővonalgyűrűkké
alakítva nincsenek a csőnek végei, azonban újabb problémák
merülnek fel. Inhomogén mágneses térben a Larmor-mozgáshoz
a térre merőleges irányú különböző driftsebesség
adódik, ahogyan azt a 4. ábra mutatja. A toroidális
tér görbülete és gradiense miatt a különböző
töltésű részecskék lefelé, illetve felfelé driftelnek. Ez töltésszétválást
okoz, és egy függőleges elektromos tér kialakulásához
vezet. Az elektromos tér egy másik driftsebességet
okoz, amely mindkét töltésű részecskére kifelé mutat a tórusz
nagysugara mentén, és így a plazma lassan elhagyja a
berendezést. Ez a probléma úgy hidalható át, hogy a mágneses
teret csavarvonalban feltekerjük a tóruszra. A le-fel
vándorló erővonalak mentén a töltésszétválás gyorsan ki
tud egyenlítődni, és a tér görbülete csak egy viszonylag kicsi
áramot okoz (Phirsch-Schlüter-áram), amelynek mágneses
tere elhanyagolható. A mai nagy fúziós berendezések
mind tórusz alakú plazmát és csavart teret alkalmaznak
(5. ábra).
A csavart térszerkezetet először a tóruszra tekert csavart
(helikális) tekercsekkel alakították ki, ez a berendezés
a klasszikus sztellarátor. A hatvanas években a moszkvai
Kurcsatov Intézetben fejlesztették ki a tokamak berendezést,
amely a helikális térszerkezetet a plazmagyűrűben
körben folyó árammal állítja elő. Ez a típus sokkal egyszerűbb
felépítésű, mint a sztellarátor (axiális szimmetriával
bír), mégis váratlanul jó részecse- és energia-összetartást
mutatott fel. Ezt az eredményt a kezdeti kétkedés után
a Kurcsatov Intézetben egy angol csoport által az akkori
legpontosabb lézerfényszórásos technikával elvégzett mérések
is igazolták, így a hetvenes években a világ minden
részén tokamak berendezések kezdtek épülni. Bebizonyosodott,
hogy bizonyos paramétertartományokban a plazma
stabil állapotban hosszú ideig, akár órákig fenntartható.
Tokamakban a folytonos működés korlátja a működéshez
szükséges plazmaáram fenntartásának nehézsége. Ezt általában
egy transzformátor segítségével indukálják, azonban
ezen a módon ez csak néhány tíz, esetleg száz másodpercig
lehetséges. Sztellarátor berendezések nem igényelnek
plazmaáramot, így ez a konfiguráció alapvetően folytonos
működésre alkalmas.
Meg kell még jegyezni egy másik alapvető különbséget
a sztellarátor és a tokamak berendezések között. A
sztellarátorban a mágneses konfigurációt alapvetően külső
tekercsekkel alakítjuk ki, ezzel szemben tokamakban a
plazmában folyó áram teszi ezt meg. Tokamakban az
áramsűrűség eloszlását a plazmában a vezetőképesség,
azt pedig a hőmérséklet-eloszlás alakítja ki. A mágneses tér
geometriája meghatározza a plazma hőszigetelését, így a
hőmérséklet-eloszlást. Végül tehát a mágneses tér geometriája
visszahat önmagára. Az már a kutató szerencséje,
hogy bizonyos paramétertartományokban ez az önszabályzó
rendszer stabil állapotba áll be. Vannak viszont
olyan tartományok, ahol a visszacsatolás pozitív és a kon-
figuráció összeomlik. Ez a diszrupciós instabilitás, amely
a tokamakoknál bizonyos paramétertartományokban jelen
van. A legtöbb esetben csak a plazma középső
részét perturbálja,
azonban bizonyos határok átlépésénél a plazma
ezredmásodperc alatt kitör a mágneses csapdából és teljes
energiáját leadja a berendezés falára. Diszrupciós instabilitások
árammentes sztellarátor-konfigurációkban nincsenek.
A fenti gondolatmenet rávilágított arra, hogy a fúziós
plazmákban a részecskék kollektív viselkedése mennyire
fontos. A plazmát felfoghatjuk áramvezető gázként is,
amely a magnetohidrodinamika (MHD) egyenleteinek
megfelelően mozog. Ez a közelítés sokszor nagyon jó
eredményt is ad, például a plazma erőegyensúlyi állapotait
jól ki lehet vele számolni. Ezek a számítások azt mutatják,
hogy a plazma nkT kinetikus nyomását a mágneses
tér B2/2µ0 mágneses nyomása egyensúlyozza ki. Mivel
a mágneses tér nagyságát a tekercsek mechanikai szilárdsága
néhány teslára korlátozza, a T hőmérsékletnek pedig
a fúziós reakciókhoz 10 keV nagyságrendűnek kell lennie,
láthatjuk, hogy a plazma sűrűségének kisebbnek kell lennie
egy meghatározott értéknél. Ez nagyságrendileg 1020 m-3-
nél következik be, ami a normál légköri sűrűségnek csak
milliomod része. Ezen a sűrűségen és hőmérsékleten a részecskék
átlagos szabad úthossza akár száz méter is lehet,
így a mágneses erővonalak mentén a hőmérséklet és sűrűség
gyorsan kiegyenlítődik. Mivel a csavarodó erővonalak
tóruszfelületet rajzolnak ki (ezeket hívjuk mágneses felületeknek,
ld. a 6. ábrát), ezért a plazma sűrűsége és
hőmérséklete is kiegyenlítődik ezeken az egymásba ágyazott
tóruszfelületeken, és a plazmaegyensúly számítása egydimenziós
problémára redukálható. Az így kiszámolt egyensúlyi
állapotok azonban nem mindig stabilak. MHD közelítésben
megvizsgálhatjuk különböző perturbációk stabilitását,
és meghatározhatók azok a mágneses konfigurációk
és maximális nyomásértékek, amelyek esetén a plazma stabil
állapotban marad. Ezeknek a számításoknak az eredményeit
a kísérletek igazolták, és így stabil tokamak- és
stellarátor-konfigurációk jól tervezhetők.
A hosszú szabad úthosszak azonban problémát is
okoznak, ugyanis nyilvánvalóan ellenkeznek a folyadékleírás
alapvetően lokális hatásokat feltételező modelljével.
Ennek megfelelően meg is jelennek olyan jelenségek
és instabilitások, amelyeket az MHD elmélet nem
tud magyarázni és kinetikus vagy egyrészecske-számolást
igényelnek. További probléma az MHD számításokhoz
szükséges transzportparaméterek (hővezetés, diffúzió, ... )
meghatározása, amelyeket az egyrészecske-mozgások és -
ütközések határoznak meg. Ezek kiszámítása bonyolult
numerikus algoritmusokkal lehetséges, amelyeket a 60-as
70-es évek számítógépei még nem minden esetben tudtak
végrehajtani. Az elméleti leírás szempontjából tehát a fúziós
plazmák olyan közegek, ahol a folyadék-, kinetikus és
egyrészecske-leírásra is szükség van.
Meg kell említeni, hogy a mágneses felületek között a
hő- és részecsketranszportot a részecskék ütközéséből és
driftmozgásából kiszámító, ún. neoklasszikus transzportelmélet
közönséges diffúziós egyenletekre vezet. Ennek
alapja könnyen érthető, ha meggondoljuk, hogy a Larmor-mozgás
a részecskéket lényegében egy mágneses erővonalhoz
köti. Egy ütközés a részecske térre merőleges sebességének
irányát véletlenszerűen módosítja, így a Larmor-pálya
középpontja átlagosan egy Larmor-sugárnyival ugrik
el. A mágneses térre merőlegesen (vagyis a mágneses
felületeken keresztül), tehát véletlen bolyongás zajlik
Larmor-sugárnyi lépéshosszal. A driftmozgás ezt a képet
csak kvantitatívan módosítja, a lépéshossz bizonyos paramétertartományokban
nagyobb lesz, mint a Larmor-sugár.
A fentebb leírt toroidális konfigurációk a gyakorlatban
is használhatónak bizonyultak, és így a 70-es évektől fokozatos
technikai fejlesztés indult. Ennek eredményéről a
cikk következő részében lesz szó.
Irodalom
). Ebben az állapotban tehát a fúziós
erőmű folyamatosan működni tudna, csak az energiájukat
leadott He-magok kiszívásáról és friss D-T keverék bejuttatásáról
kell gondoskodni. Ezt az állapotot fúziós égésnek
nevezzük. Meg kell jegyezni, hogy ebben az állapotban
kevés lehetőség van a berendezés vezérlésére, ezért a kísérletek
inkább a Q = 10-30 közötti paramétertartományt
veszik célba.
A kezdetek
A Lawson-kritérium kielégítésére két úton lehet elindulni:
jó szigetelés (hosszú energia-összetartási idő) és alacsony
sűrűség, vagy igen magas sűrűségmellett rövid összetartás,
vagyis robbanás. Ez utóbbi megoldást inerciális összetartásnak
szokás nevezni, mivel egy r sugarú gömb körülbelül
r/cs ideig mindenképpen egyben marad (ahol cs a közegbeli
hangsebesség). A Lawson-kritérium állandó állapotot
tételez fel, így az inerciális fúzió esetére nem érvényes,
mégis az erre vonatkozó megfontolások arra vezetnek,
hogy a megvalósításhoz a szilárdtest-sűrűség körülbelül
ezerszeresét kell elérni. Ezt a sűrűséget kisméretű kapszulák
lézeres, röntgensugárzásos vagy részecskenyalábos
összenyomásával próbálják elérni. Ennek során olyan extrém
állapotba kell vinni az anyagot, ami a Földön leginkább
nukleáris robbantások alkalmával jön létre, így nem
csoda, hogy az inerciális fúziós kutatások sok ponton kapcsolódnak
katonai fejlesztésekhez, és így nem teljesen nyilvánosak.
Lézeres fúziós célra jelenleg két nagy berendezés
is épül (NIF, USA és LMJ, Franciaország), és ezek a tervek
szerint egy-egy kapszulából pozitív energiamérleget is
fognak elérni [2]. Ennek ellenére ilyen alapú reaktor
megépítése
távolinak tűnik. Az inerciális fúziós kutatások önmagukban
is egy külön cikket igényelnének, ezért velük itt
a továbbiakban nem foglalkozunk.
A nagyságrendileg 10 keV (100 millió °C) hőmérsékletű fúziós közegre hosszú
energia-összetartási időt tűzve ki célul kihasználhatjuk, hogy ezen a
hőmérsékleten az anyag mindenképpen plazmaállapotban van, azaz az elektronok
leszakadnak az atommagokról. A plazma elektromágnesesen kölcsönható közeg,
így összetartásához megpróbálkozhatunk mágneses terekkel. Ilyen kutatások az
1950-es évek elején nagy titoktartás mellett indultak meg elsősorban az
USA-ban, Angliában és a Szovjetúnióban. Az évtized végére világossá vált,
hogy nem lehet gyors eredményt elérni, ilyen extrém állapotú anyagok
viselkedésének megértéséhez még alapkutatásokra is szükség van. Az
eredményeket fokozatosan nyilvánossá tették, 1
a kutatások ma már évtizedek óta széles nemzetközi együttműködésben folynak.
Mágneses plazmaösszetartás
Mágneses térben a plazma töltött részecskéi (az elektronok
és az ionok) a mágneses erővonalak körül Larmor-pályán
mozognak, ahogy azt a 3. ábra mutatja. A Larmor-pálya
sugara erős mágneses térben (kb. 1 T) még a 10 keV-es
deutérium és trícium atommagokra sem nagyobb, mint néhány
milliméter. A térre merőleges irányban a részecskék
gyakorlatilag nem tudnak elmozdulni, és mintegy csőbe
zárható a plazma. A csővégeinek "bedugaszolását"
először mágneses tükrökkel próbálták megoldani. Ezekben a
mágneses tér erőssége az erővonalak mentén növekszik. A
Larmor-pályán mozgó részecskék köráramot és ezzel
mágneses dipólust képviselnek. Erre a mágneses tér gradiense
erőt fejt ki, akárcsak egy mágnesre. Ennek eredményeképpen
a részecskék visszaverődnek a nagyobb terű tartományoktól.
Sajnos a visszatérítő erő a mágneses térhez képest kis
szögben hajló pályán futó részecskékre nem elég nagy, így
két mágneses tükör közötti tartományban a részecskéknek
csak egy része tartható össze. Az ütközések miatt az összetartott
részecskék is egy idő után olyan irányú sebességet
kaphatnak, amellyel kijutnak a berendezésből. Ezeknek
a problémáknak a kiküszöbölésére különböző elektrosztatikus
csapdák hozzáadásával kísérleteztek, de az eredmények
nem voltak túl biztatóak, így az ilyen lineáris berendezésekkel
folyó kísérleteket a 80-as évek tájékán nagyrészt feladták.
A mágneses teret tórusz alakú zárt erővonalgyűrűkké
alakítva nincsenek a csőnek végei, azonban újabb problémák
merülnek fel. Inhomogén mágneses térben a Larmor-mozgáshoz
a térre merőleges irányú különböző driftsebesség
adódik, ahogyan azt a 4. ábra mutatja. A toroidális
tér görbülete és gradiense miatt a különböző
töltésű részecskék lefelé, illetve felfelé driftelnek. Ez töltésszétválást
okoz, és egy függőleges elektromos tér kialakulásához
vezet. Az elektromos tér egy másik driftsebességet
okoz, amely mindkét töltésű részecskére kifelé mutat a tórusz
nagysugara mentén, és így a plazma lassan elhagyja a
berendezést. Ez a probléma úgy hidalható át, hogy a mágneses
teret csavarvonalban feltekerjük a tóruszra. A le-fel
vándorló erővonalak mentén a töltésszétválás gyorsan ki
tud egyenlítődni, és a tér görbülete csak egy viszonylag kicsi
áramot okoz (Phirsch-Schlüter-áram), amelynek mágneses
tere elhanyagolható. A mai nagy fúziós berendezések
mind tórusz alakú plazmát és csavart teret alkalmaznak
(5. ábra).
A csavart térszerkezetet először a tóruszra tekert csavart
(helikális) tekercsekkel alakították ki, ez a berendezés
a klasszikus sztellarátor. A hatvanas években a moszkvai
Kurcsatov Intézetben fejlesztették ki a tokamak berendezést,
amely a helikális térszerkezetet a plazmagyűrűben
körben folyó árammal állítja elő. Ez a típus sokkal egyszerűbb
felépítésű, mint a sztellarátor (axiális szimmetriával
bír), mégis váratlanul jó részecse- és energia-összetartást
mutatott fel. Ezt az eredményt a kezdeti kétkedés után
a Kurcsatov Intézetben egy angol csoport által az akkori
legpontosabb lézerfényszórásos technikával elvégzett mérések
is igazolták, így a hetvenes években a világ minden
részén tokamak berendezések kezdtek épülni. Bebizonyosodott,
hogy bizonyos paramétertartományokban a plazma
stabil állapotban hosszú ideig, akár órákig fenntartható.
Tokamakban a folytonos működés korlátja a működéshez
szükséges plazmaáram fenntartásának nehézsége. Ezt általában
egy transzformátor segítségével indukálják, azonban
ezen a módon ez csak néhány tíz, esetleg száz másodpercig
lehetséges. Sztellarátor berendezések nem igényelnek
plazmaáramot, így ez a konfiguráció alapvetően folytonos
működésre alkalmas.
Meg kell még jegyezni egy másik alapvető különbséget
a sztellarátor és a tokamak berendezések között. A
sztellarátorban a mágneses konfigurációt alapvetően külső
tekercsekkel alakítjuk ki, ezzel szemben tokamakban a
plazmában folyó áram teszi ezt meg. Tokamakban az
áramsűrűség eloszlását a plazmában a vezetőképesség,
azt pedig a hőmérséklet-eloszlás alakítja ki. A mágneses tér
geometriája meghatározza a plazma hőszigetelését, így a
hőmérséklet-eloszlást. Végül tehát a mágneses tér geometriája
visszahat önmagára. Az már a kutató szerencséje,
hogy bizonyos paramétertartományokban ez az önszabályzó
rendszer stabil állapotba áll be. Vannak viszont
olyan tartományok, ahol a visszacsatolás pozitív és a kon-
figuráció összeomlik. Ez a diszrupciós instabilitás, amely
a tokamakoknál bizonyos paramétertartományokban jelen
van. A legtöbb esetben csak a plazma középső
részét perturbálja,
azonban bizonyos határok átlépésénél a plazma
ezredmásodperc alatt kitör a mágneses csapdából és teljes
energiáját leadja a berendezés falára. Diszrupciós instabilitások
árammentes sztellarátor-konfigurációkban nincsenek.
A fenti gondolatmenet rávilágított arra, hogy a fúziós
plazmákban a részecskék kollektív viselkedése mennyire
fontos. A plazmát felfoghatjuk áramvezető gázként is,
amely a magnetohidrodinamika (MHD) egyenleteinek
megfelelően mozog. Ez a közelítés sokszor nagyon jó
eredményt is ad, például a plazma erőegyensúlyi állapotait
jól ki lehet vele számolni. Ezek a számítások azt mutatják,
hogy a plazma nkT kinetikus nyomását a mágneses
tér B2/2µ0 mágneses nyomása egyensúlyozza ki. Mivel
a mágneses tér nagyságát a tekercsek mechanikai szilárdsága
néhány teslára korlátozza, a T hőmérsékletnek pedig
a fúziós reakciókhoz 10 keV nagyságrendűnek kell lennie,
láthatjuk, hogy a plazma sűrűségének kisebbnek kell lennie
egy meghatározott értéknél. Ez nagyságrendileg 1020 m-3-
nél következik be, ami a normál légköri sűrűségnek csak
milliomod része. Ezen a sűrűségen és hőmérsékleten a részecskék
átlagos szabad úthossza akár száz méter is lehet,
így a mágneses erővonalak mentén a hőmérséklet és sűrűség
gyorsan kiegyenlítődik. Mivel a csavarodó erővonalak
tóruszfelületet rajzolnak ki (ezeket hívjuk mágneses felületeknek,
ld. a 6. ábrát), ezért a plazma sűrűsége és
hőmérséklete is kiegyenlítődik ezeken az egymásba ágyazott
tóruszfelületeken, és a plazmaegyensúly számítása egydimenziós
problémára redukálható. Az így kiszámolt egyensúlyi
állapotok azonban nem mindig stabilak. MHD közelítésben
megvizsgálhatjuk különböző perturbációk stabilitását,
és meghatározhatók azok a mágneses konfigurációk
és maximális nyomásértékek, amelyek esetén a plazma stabil
állapotban marad. Ezeknek a számításoknak az eredményeit
a kísérletek igazolták, és így stabil tokamak- és
stellarátor-konfigurációk jól tervezhetők.
A hosszú szabad úthosszak azonban problémát is
okoznak, ugyanis nyilvánvalóan ellenkeznek a folyadékleírás
alapvetően lokális hatásokat feltételező modelljével.
Ennek megfelelően meg is jelennek olyan jelenségek
és instabilitások, amelyeket az MHD elmélet nem
tud magyarázni és kinetikus vagy egyrészecske-számolást
igényelnek. További probléma az MHD számításokhoz
szükséges transzportparaméterek (hővezetés, diffúzió, ... )
meghatározása, amelyeket az egyrészecske-mozgások és -
ütközések határoznak meg. Ezek kiszámítása bonyolult
numerikus algoritmusokkal lehetséges, amelyeket a 60-as
70-es évek számítógépei még nem minden esetben tudtak
végrehajtani. Az elméleti leírás szempontjából tehát a fúziós
plazmák olyan közegek, ahol a folyadék-, kinetikus és
egyrészecske-leírásra is szükség van.
Meg kell említeni, hogy a mágneses felületek között a
hő- és részecsketranszportot a részecskék ütközéséből és
driftmozgásából kiszámító, ún. neoklasszikus transzportelmélet
közönséges diffúziós egyenletekre vezet. Ennek
alapja könnyen érthető, ha meggondoljuk, hogy a Larmor-mozgás
a részecskéket lényegében egy mágneses erővonalhoz
köti. Egy ütközés a részecske térre merőleges sebességének
irányát véletlenszerűen módosítja, így a Larmor-pálya
középpontja átlagosan egy Larmor-sugárnyival ugrik
el. A mágneses térre merőlegesen (vagyis a mágneses
felületeken keresztül), tehát véletlen bolyongás zajlik
Larmor-sugárnyi lépéshosszal. A driftmozgás ezt a képet
csak kvantitatívan módosítja, a lépéshossz bizonyos paramétertartományokban
nagyobb lesz, mint a Larmor-sugár.
A fentebb leírt toroidális konfigurációk a gyakorlatban
is használhatónak bizonyultak, és így a 70-es évektől fokozatos
technikai fejlesztés indult. Ennek eredményéről a
cikk következő részében lesz szó.
Irodalom