Fizikai Szemle 2005/9. 328.o.

MEGJEGYZÉS EGY RELATIVITÁSELMÉLET-ÉRTELMEZÉSHEZ

A relativitáselmélet logikai-filozófiai irodalma azonkívül hogy terjedelmes, nem tartozik éppen a könnyű olvasmányok közé, de én is azok közé tartozom akik újra és újra próbálják megérteni, és nagyon hálás vagyok, ha egy fizikus vagy matematikus, aki a terület szakérője, megpróbál ebből elmagyarázni annyit, amennyit lehet. Viszont zavarban vagyok akkor, amikor jön egy másik szakértő, és azt mondja nekem, hogy amit a többiek mondanak tévedés. Kinek higgyek, merjek-e ellentmondani, mikor könnyen lehet, hogy meg sem értem vagy félreértem amit mond? Pedig nem kell az elméleti fizika rejtelmeibe bonyolódjunk, hogy ne értsük egymást. A minap helyettem feleségem vitte vissza a kollégiumba lányomat, és ezért elmagyaráztam neki az utat autós szemmel. "Fordulj az Irinyi József útról jobbra az Október 23. útra, majd onnan az áruház előtt egy másodszori jobbra fordulással a Bercsényi utcába." Miután hazaért, összeszidott, hogy miért mondtam, hogy kétszer kell jobbra fordulni, amikor valójában csak egyszer kellett? Hüledezve hallgattam, és próbáltam meggyőzni, hogy bizonyára először kis ívben fordult jobbra a Budafoki út után, majd másodszor is jobbra a kollégium utcájába. "Nem-nem" - volt a válasz - "rosszul emlékszel, csak egyszer kell jobbra fordulni, mert a kollégium utcájáig egyenes az út". Jövő héten mérgemben én vittem vissza a lányomat, feleségemet pedig magam mellé ültettem az autóba. Mikor éppen elhagytam a Budafoki utat, és először kezdtem jobbra kanyarodni, megkérdeztem, látja-e, hogy a kormányt folyamatosan jobbra tekerem. "Az nem számít" - volt a válasz - "mert nem indexelsz". Ekkor megértettem, hogy közöttünk szemantikai diszkrepancia van (húsz évi házasság után), mást ért egyenesen, illetve jobbra forduláson, mint én. Szerencsére ebben az esetben a "jobbra fordulni" referenciája azért kifürkészhetőnek tűnt, ő a KRESZ szerint értelmezte a jobbra fordulást, míg én geometriai értelemben. Ez jutott eszembe, amikor elolvastam az E. Szabó Lászlóval készült beszélgetést, melynek címe önmagáért beszél: Semmiben nem nyújt új vagy más leírást a térről és az időről a speciális relativitáselmélet, mert arról van szó.¹ Megismétlem, azt állítja: semmiben. Ha semmiben, akkor az érthetőségben sincs különbség, de akkor miért értik meg az előbbit sokkal könnyebben az emberek, mint az utóbbit? Miért vitatkozunk mi itt erről és nem a régi fizikáról? Biztos tökéletesen mást ért "újdonság" alatt, ha szerinte a speciális relativitáselmélet semmi újat nem tartalmaz a klasszikus fizikához képest. Nyilván éppen olyan jól tudja, mint én, hogy a klasszikus fizika és a speciális relativitáselmélet más-más modellt használ. Einstein ezt egy mára klasszikussá vált vonatos példával világosan elmagyarázza. A klasszikus fizika így számol, míg a relativitás úgy, a kettő nyilvánvalóan nem azonos. Mondhatjuk-e ezek után mégis, hogy ennek ellenére a két modell, melynek folyománya a két eltérő formula, valójában azonos? Mit jelent itt ez a "valójában"? Csodálkozásom csak fokozódott, amikor ezek után a cikket olvasva a következő részhez értem: "Tehát a lényeg, és ez az, aminek a meg nem értéséből az a sok »bizsergés« fakad, hogy Einstein a relativitáselméletben más fizikai mennyiséget nevez »távolságnak« és »időnek« mint a klasszikus fizika." De ha ez így van, akkor miért mondja, hogy semmi új nincs ebben az elméletben, hisz legalábbis az alapvető terminusok "idő, távolság" jelentése eltér? Mondhatja, hogy neki ellenszenves ez a felfogás, sőt azt is, hogy jogosulatlan, mert ezek jelentése már rögzített a köznapi nyelvben, aztán mondhatja, hogy célszerűtlen, túl bonyolult, vagy túl egyszerű, vagy akár azt is, hogy elfogadhatatlan metafizikai előfeltevéseket implikál. Egyetlenegy dolgot nem mondhat: egy létezőről nem állíthatja, hogy nem létezik mikor az létezik; azaz, ha van itt valami új, akkor nem mondhatja, hogy nincs. Ez azonban nyilvánvaló ellentmondás volna, amit feltehetőleg ő is átlát, ezért biztos, nem így gondolja, amit gondol, és én értem félre. Azért gondolom, hogy a most fölvázolt értelmezésemben hibának kell lennie, mert különben önellentmondást tartalmazna E. Szabó gondolatmenete. Mivel ez nem valószínű, tehát el kell vetnem a saját értelmezésemet, amely ide vezetett. De akkor mire gondolhat? Szerencsére elmagyarázza, legalábbis megpróbálja. Azt javasolja, ne fogadjuk el Einstein terminus-használatát, nevezzük másképp azt, amit Einstein időn és távolságon ért, és akkor rá fogunk döbbeni, hogy nincs itt semmi új a régi mechanikához képest. Szerinte ugyanis a relativitáselmélet időfogalma más, mint a klasszikus fizikáé, amiben igaza van. Meggyőződése szerint talált olyan leképezést a klasszikus és a relativitáson alapulótér-idő modell között, hogy az összefüggések izomorfok lesznek. (Két szerkezet izomorf, ha a benne lévő elemek és kapcsolataik kölcsönösen egyértelmű viszonyba hozhatók.) De mit jelent pontosabban ez az izomorfiaű Mit jelent jobbra kanyarodni?

Még ennél is sokkal többet állít E. Szabó. Azt állítja, hogy a speciális relativitáselmélet önellentmondásos. Ezt írja: " .... mit is jelent magyarul az, hogy az órák lelassulása és a méterrudak megrövidülése »kimagyarázza« a Michelson- Morley-kísérlet eredményét? Ez azt jelenti, hogy ha a méterrudak megrövidülése stb. fennáll, akkor a Michelson- Morley-kísérlet eredményéből az következik, hogy a fény sebessége nem ugyanaz minden inerciarendszerben (hanem c+v, c=v, ahogyan azt a klasszikus fizika gondolja). Mármost a relativitáselmélet két alapelve közül az egyik az a tézis, hogy a fény terjedési sebessége minden inerciarendszerben azonos. Mint bármelyik standard tankönyvben elolvasható, e két alapelvből rövid úton következik, hogy a méterrudak megrövidülnek stb., amiből viszont következik - a Michelson-Morley-kísérletben tapasztaltak alapján -, hogy a fény terjedési sebessége nem azonos minden inerciarendszerben. Ez logikai ellentmondás, amely indirekt módon azt bizonyítja, hogy a relativitáselmélet két alapelve közül az egyik nem lehet igaz. "Szellemes érvelés, de érvényes-e? Vizsgáljuk meg alaposabban. Ez a következtetés azon alapul, hogy E. Szabó szerint a relativitáselméletben némelyik esetben a merev testek lerövidülnek: " .... nem pontosan ezt mondja az Einstein-féle, vagyis a ma általánosan elfogadott relativitáselmélet, hogy a mozgóméterrúd megrövidül, éppen az említett mértékben, és a mozgó óra lelassul, éppen úgy, ahogyan azt Fitzgerald és Lorentz feltételezték?" Nem, Einstein nem ezt mondja. A relativitáselmélet arról beszél, hogy a méterrudak hossza mindig adott vonatkoztatási rendszerben értendő. (A "vonatkoztatási rendszer" és "koordináta-rendszer" kifejezéseket egymás szinonimáinak tekintem.) A merev test önmagához rögzített koordináta-rendszerében nem változik a rúd hossza, de egy hozzá képest mozgómásik inerciarendszerben már igen, onnan mérve más a test hossza. Nem igaz, amit E. Szabó állít, hogy a mozgórúd megrövidül csak úgy általában véve, valójában a mozgó rúd hossza egy másik, hozzá képest mozgó rendszerben mérve rövidül meg. Így, mivel ez az állítása hamis, az egész érvelése összeomlik. Érdekes, hogy nem merül föl E. Szabó Lászlóban, mint bennem az ő szövege értelmezése során, hogy talán nem jól értem, amit olvasok, azért látok ellentmondást. Vegyük elő ismét az egyik klasszikus szöveget, amelyre E. Szabó is hivatkozik, és elfogulatlanul, ráhagyatkozással olvassuk újra. Higgyük el, akar nekünk mondani valamit, valamit, ami nem egyszerű, nem könnyen érthető, de mégis minket kézen fogva, lépésről lépésre vezetve fölvisz olyan magasságba, ameddig mi szerény matematikai ismeretekkel fölvértezve követni tudjuk. Ezt írja Einstein: "Nincs tehát &;raquo;önmagában vettlaquo; pályagörbe (olyan görbe, amelyen a test mozog), hanem csakis meghatározott testhez viszonyított pályagörbéről lehet beszélni." ² Novobátzky Károly megjegyzése ehhez: "Ezt a tényt így szokás kifejezni: a pályagörbe nem abszolút, hanem relatív fogalom. Két különböző koordináta-rendszerben a pályagörbe más és más."³ A következő passzusban ismét figyeljünk föl arra, hogy Einstein mindenütt viszonyokról, relációkról beszél. Ezt mondja az időről: "Miután azonban az az idő, amelyre egy bizonyos történésnek a vonathoz viszonyítva szüksége van, az imént közölt meggondolások szerint nem lehet egyenlő ugyanennek a történésnek a töltésre vonatkoztatott tartalmával, nem állíthatjuk tehát, hogy a vasúti kocsiban járkálóutas a pályatesthez viszonyítva a w útdarabot olyan idő alatt teszi meg, amely - a töltésről nézve - egy másodperccel egyenlő".⁴ Újra csak viszonyokról beszél a relativitáselmélet megalkotója, és nyilvánvalóan innen van az elmélet elnevezése is! Vajon hogyan gondolkozik a távolságrólű Valóban úgy, ahogy E. Szabó László értelmezi? Ez fontos kérdés, mert mint említettem, több következtetése ezen az értelmezésen alapul. Ehhez egy kis kitérőt kell tegyünk. Fontos, hogy megkülönböztessünk egymástól egy elméletet, egy szellemi alkotást - a relativitáselméletet - és azokat a kísérleteket, megfigyeléseket melyek magyarázatára ez az elmélet született. Az elmélet - jelen esetben a speciális relativitáselmélet - értelmezése éppúgy fölvet kérdéseket, értelmezéssel kapcsolatos vitákat, mint a kísérletek, mérések értelmezése, röviden, a valóság értelmezése, magyarázata. Einstein szövege, mint sok más szöveg, néha többértelmű, egymással ellentétes értelmezéseket is megenged. Ennek ellenére próbáljuk meg megérteni, mit gondolt Einstein, és ez nem azonos azzal a kérdéssel, hogy igaza volt-e, vagy nem volt igaza, avagy lehet-e másképp is magyarázni azokat a jelenségeket, amelyeket ő magyaráz. A most forrásértékűnek tekintett szélesebb nagyközönség számára írt könyvecskében Einstein többször is beszél a távolságok megrövidüléséről, kérdés azonban, hogy pontosan hogyan érti azt? Így ír ezzel kapcsolatban egy fontos helyen: "Lorentz és Fitzgerald azzal a feltevéssel mentette ki az elméletet a zavarból, hogy az éterrel szemben végzett mozgás eredményeképpen a test a mozgás irányában összehúzódik; ennek az összehúzódásnak kellett eltüntetnie az előbb említett időkülönbözetet. A 12. fejezetben mondottakkal összehasonlítva láthatjuk, hogy ez a megoldás a relativitáselmélet szempontjából is helyénvaló volt. A tényállásnak a relativitás szerinti felfogása azonban összehasonlíthatatlanul kielégítőbb. (Ezek szerint a relativitás másképp értelmezi a rövidülést! A.F.) Mert eszerint nincs a többiek között kitüntetett szerepet játszóolyan koordináta-rendszer, amely az éter fogalmának bevezetésére okot adna; és így nincs »éterszél« sem; olyan kísérlet sincs, amelyből ennek létezése következnék. A mozgótestek összehúzódása itt minden különösebb hipotézis nélkül az elmélet két alapelvéből következik; mégpedig erre az összehúzódásra nem a magában vett mozgás mérvadó, (kiemelés tőlem) melynek nem tulajdoníthatunk értelmet, hanem mindenkor a választott vonatkoztatási testhez viszonyítva végzett mozgás (kiemelés tőlem). Így tehát Michelson és Morley tükrös testje a Földdel együtt mozgórendszerből nézve nem rövidül meg, de igenis megrövidül a Naphoz képest nyugvó rendszerben."⁵ Világos beszéd, a rövidülés relatív és nem abszolút. Az, hogy valami relatív, azaz relációs logikai szerkezetű, nem azt jelenti, hogy szubjektív, az elméről vagy az érzékelésről szóló kijelentés. A falban lévő egyik vezeték elektromos feszültsége egy adott ponthoz képest 230 V, míg egy másik ponthoz képest 400 V. Ha valaki azt kérdezné ezek után, hogy "igen, de mennyi valójában?", ezzel azt fejezné ki, hogy nem értette meg eme tény relációs (viszony) jellegét. Figyeljünk föl erre, amikor Einstein a "magában vett mozgás" fogalmának értelmetlenségéről beszél, és helyette a "választott vonatkoztatási testhez" viszonyított mozgásról beszél a testek, a távolság megváltozásával kapcsolatban. A könyv egy korábbi helyén két axiómát fogalmaz meg, amelyek részei a klasszikus fizikának, de az új elméletben nem alkalmazandók:

"Az utóbbi három fejezet megfontolásai azt mutatták, hogy a fényterjedés törvénye és a relativitás közti látszólagos ellentmondás a 7. fejezetben oly meggondolásokból adódott, amely a klasszikus mechanikából két, egyáltalán nem indokolt feltevést vett át. E feltevések:

1. Két esemény időköze független a vonatkozótest mozgásállapotától.
2. A merev test két pontjának térbeli távolsága független a vonatkozó test mozgásállapotától.

Ha elejtjük e feltevéseket, úgy a 7. fejezet dilemmája megszűnik, .... "⁶

Itt most a második kijelentés elvetése az érdekes számunkra. Azt mondja, hogy a térbeli test két pontjának távolsága a vonatkoztató test mozgásállapotától függ. Csakhogy több vonatkoztató test is lehetséges, és ezért az egyik esetben a távolság ennek, a másik esetben pedig annak adódhat. Ez azért nem ellentmondás, mert a különböző számok különböző vonatkozásokban értendők. Éppen ebben van a távolság fogalmának relációs jellege a relativitáselméletben. Nézzünk további szöveghelyeket. Nevezetes 1905-ös cikkében írja: "Az olyan merev test tehát, amely nyugalmi állapotban gömb alakú, mozgó állapotban - a nyugvórendszerből szemlélve - forgási ellipszoid alakú .... "⁷ Ismét csak azt mondja, a rövidülés relatív és nem abszolút. Van olyan hely is, ahol Einstein valóban a rúd megrövidüléséről beszél:

"K-hoz képest a méterrúd azonban v sebességgel mozog. Tehát egy hosszirányban v sebességgel mozgó merev méterrúd hossza csak méter. Azaz a mozgómerev rúd annál rövidebb, minél gyorsabban mozog."⁸ Novobátzky Károly azonban felhívja a figyelmünket a szerinte helyes értelmezésre. "A rúd rövidülésével kapcsolatban felmerül az az érdekes kérdés, történt-e a rúddal valamilyen belső objektív változás? Felelet: a rúddal nem történt semmi. A bizonyítás nagyon egyszerű. Feküdjék a rúd nyugalomban a töltésen. Hossza ott lemérve legyen 1 méter. Most vonat halad el mellette v sebességgel. A vonatról mérve a hossza . Ha egy párhuzamos vágányon ugyanakkor egy másik vonat halad el mellette nagyobb V sebességgel, onnan mérve a hossza adódik, vagyis kisebbnek. Ha tehát a rúd megrövidülése objektív valóság volna, egyszerre két különböző hosszúsággal kellene rendelkeznie, ami képtelenség. A helyes értelmezés a következő: a rúddal ténylegesen nem történik semmi, de hosszának mérőszáma különbözőnek adódik aszerint, hogy a (vonaton levő) mérőszalag más-más sebességgel mozog hozzá képest. Feltétlen el kell vetnünk azt a tévedést, mintha a rúd nyugalmi hossza az igazi hosszúság volna. A vonaton levő megfigyelő számára a rúd hossza az általa megállapított mérőszám."⁹ (Ez utóbbi mondatot vitathatónak tartom. Miért ne lehetne kitüntetett szerepe egy merev test önmagához rögzített koordináta-rendszerben mért jellemzőinek? Ez szerintem definíció kérdése.) Ellentétben E. Szabó Lászlóval, úgy vélem Novobátzky Einstein szellemében fűzte ezt a megjegyzést az eredeti szöveghez. (A könyvet Károlyházi Frigyes lektorálta szakmailag. Így aki Novobátzkyt leszólja, Károlyházit is megszólja.) Az az értelmezés tehát, hogy egy tárgy alakja önmagában megváltozik a mozgás következtében, és nem csak a gyorsítás alatt, hanem utána is, amikor már állandó sebességgel halad, bár különös, de talán lehetséges értelmezése a kísérleteknek, viszont nem annak, amit Einstein ír.

Melyek a speciális relativitáselmélet alapelvei? Alapelve-e a fénysebesség állandósága minden inerciarendszerben? E. Szabó itt is meglep bennünket: "Ez a tézis nem azonos azzal, amit hallani szerettél volna, hogy a fény sebessége azonos minden inerciarendszerben. Mert az nem igaz. És azt a relativitáselmélet sem mondja. (Nem gondolom, hogy ennek jelentősége van, csak érdekességképpen jegyzem meg, hogy ez az állítás nem is szerepel Einstein 1905-ös cikkében.)" - írja. Nézzük, mit írt Einstein 1905- ben A mozgó testek elektrodinamikájáról című cikkében: "Az alábbi fejtegetések a relativitáselven és a fénysebesség állandóságának elvén alapulnak. A két elvet az alábbiak szerint definiáljuk: ...."¹⁰ Majd a nagyközönségnek írt munkájában így fogalmazza meg az új teória feladatát: "Hogyan kapjuk meg egy eseménynek a vonathoz viszonyított helyét és idejét, ha ismerjük ugyanannak az eseménynek a vasúti töltésre vonatkoztatott helyét és idejét? Megfelelhetünk- e erre a kérdésre úgy, hogy a vákuumbeli fényterjedés törvénye ne ellenkezzék a relativitás elvével?"¹¹ Mintha ez a két idézet cáfolná E. Szabó állítását. Ami a fénysebesség, illetve általában egy felső határsebesség létét illeti, attól is függ, hogy folytonos szerkezetűnek, avagy diszkrét mennyiségnek feltételezzük a teret és az időt. Az utóbbi esetében meg fogom mutatni, hogy a felső határsebesség létezése mellett logikai érvek is szólnak.

A világűr egy távoli szegletében távol minden csillagtól párhuzamos (egyenes) vágányok indulnak a végtelenbe egy állomásról. A szerelvényeken indulás előtt ellenőriztük a klasszikus mechanika törvényeit, és különféle, pontosan egyforma órákat helyeztünk el a vonatokon. Van ezek között felhúzós mechanikus vekker, digitális óra, sőt még a fényóra is, amely két szembefordított tükör között oda-vissza cikázófénysugárral méri az időt. (Ahogy Feynman leírja a Mai fizika című könyv 2. kötetében.) Az órák azonkívül, hogy azonos ritmusra járnak, azonos időt is mutattak indulás előtt. A hosszú úthoz képes rövid gyorsítás után a vonatok különféle állandósebességet értek el, és azzal folyamatosan haladtak a végállomásig, majd onnan visszatértek a kiindulópontba. Az egyik vonatot nem indítottuk el, az helyben maradt. Ennek óráit összehasonlítottuk a visszatért vonatok óráival, és a következőt tapasztaltuk: az órák továbbra is azonos ütemben járnak, viszont kiestek a szinkronból, annál jobban késnek, minél gyorsabban tették meg az utat. Távolságokat is mértünk a vonatokon. Megmértük a szerelvények hosszát az indulás előtt, majd a vonatokra fölszállva a gyorsítás alatt és az utazási sebességen is. A középső esetet kivéve nem találtunk eltérést, és a visszaérkezett vonatok hossza is változatlan. A gyorsítás alatt mértünk eltérést, de ez nem meglepő az ismert fizikai törvények ismeretében. Viszont egy távoli bakterháznál megfigyelőt jelöltünk ki azzal a feladattal, hogy ő is mérje meg az előtte elszáguldó szerelvények hosszát. Érdekes módon ő a nyugalmi állapotnál rövidebbnek mért minden mozgó vonatot. Ezzel szemben mi a vonaton nem tapasztaltunk sem rövidülést, sem az órák deformálódását. Mondhatjuk-e ezek után E. Szabóval egyetértésben, hogy az idő egyformán telt a száguldó és álló vonatokon, csak a mérésére szolgált eszközökkel történt valami különös? Einstein nemmel válaszolt a kérdésre, mások - köztük a vitatott írás szerzője - igennel. Mondhatjuk-e, hogy azért mérte a megfigyelő rövidebbnek a vonatot, mert az attól függően, hogy milyen gyorsan haladt, megrövidült? Einstein szerint igen, a töltéshez képest, és nem, a vonaton ülve. Az ellentétes vélemény szerint a vonat miközben száguld, megrövidül, amit rajta ülve ezért nem veszünk észre, mert a mérés alapját jelentő méterrúd is rövidebb lesz. Lehet-e választani a két felfogás között, avagy mindkettő helyes? Wittgenstein szerint nemhogy az etalonok rövidülésének, de még annak a kijelentésnek sincs értelme, hogy az etalon 1 m-es rúd 1 méter. Ha egy fémből készült 1 m-es rúd hossza megváltozik melegítés hatására, ennek azért tulajdoníthatunk értelmet, mert mellé tehetünk egy másik, vele egyforma rudat, amelyet nem melegítettünk föl, és láthatjuk az eltérést. Azt is megfigyelhetjük, amint a fölmelegített rúd lehűl, és visszanyeri eredeti hosszát, újból létrejön a két rúd hosszának egyenlősége. Egy gyorsan haladó rendszerben viszont lehetetlen egy álló rendszerben lévő rudat a másik mellé helyezni, így a rudak saját hosszának E. Szabó által feltételezett rövidülése a megfigyelhetetlen jelenségek körébe tartozik.

Kis lépést téve a probléma tudományos megközelítése felé, miképpen írhatjuk le pontosabban az előbbi elképzelt kísérletet? A helyben maradt vonatot nevezzük k-nak, egy mozgóvonatot pedig kű-nek, de miképpen jelöljük a vonatokon mért helyet és időtű Nem biztos, hogy ez lényegtelen. Egy alkalmas jelölés segíthet a világos megértésben, míg egy alkalmatlan egyenesen félrevezethet. A kísérlet leírására milyen nyelvi keretet válasszunk? Ezek megvitatása már túlmutat az én hozzáértésemen, de bizonyos összefüggéseket látni vélek. Két fogalmat vázolok fel. Az idő értelmezése szoros kapcsolatban áll az egyidejűség értelmezésével. Az "egyidejűség" szintaxisa a klasszikus fizikában így fest: x egyidejű y -nal, ezzel szemben Einsteinnél így: x egyidejű y -nal a k vonatkoztatási rendszerben. Mint látható, az utóbbi kifejezés argumentumszáma eggyel több, mint az előbbié. A klasszikus fizika vonatkozó feltevése megfogalmazható a második terminussal: ha van olyan k, melyre x egyidejű y -nal k-ban, akkor minden k₁-re x egyidejű y -nal k₁-ben. Ezek alapján bevezetve a klasszikus egyidejűségre a "koinc₁" az újra a "koinc₂" kifejezéseket, a kettő kapcsolatának egy lehetséges megfogalmazása így festhet: koinc₁ (x,y ) = van olyan k, hogy koinc₂ (x,y ; k), ahol k tetszőleges inerciarendszer, x, y pedig állapotok, események. Mint látható, a relativitáselmélet "egyidejűség"-fogalma felülről lefedi a klasszikus "egyidejűség"-fogalmat, hiszen definiálható benne. Ezért a klasszikus és a relativisztikus "idő"-fogalom között sincs kibékíthetetlen ellentét, a relativisztikus időfogalom egy alesete a hagyományos időfogalom. Mint jól ismert, ez a számszerű összefüggésekből is látszik, ha a fénysebességet végtelen nagynak képzeljük.

Egy test helye már a klasszikus fizikában is relációs fogalom, de a hosszúsága nem. A relativitáselmélet egy merev test hosszúságát mindig egy koordináta-rendszerhez való viszonyában értelmezi, míg a klasszikus fizika felfogása ezt vonatkoztatási rendszertől függetlennek tekinti, más értelemben, azonosnak veszi minden koordináta- rendszerben. A logikai szerkezet (szintaxis) szempontjából ez azt jelenti, hogy amíg a klasszikus fizika az objektumok tulajdonságának tekinti egy merev test hosszát, addig a modern fizika ezt a fizikai jellemzőt viszonyként (relációként) értelmezi. Ha ebben a relációban kitüntetjük a merev testek önmagukhoz rögzített vonatkozatási rendszerét, akkor az ezekben mért jellemzőt azonosíthatjuk a klasszikus fizika "hossz"-fogalmával. Avagy logikai megközelítésben, ha egy kétargumentumú relációegyik argumentumát kitöltjük, akkor egyargumentumú predikátumot (tulajdonságot) kapunk. A relativisztikus gondolkodásmód itt is felülről lefedi a régi fizikát, gazdagabb nála. Ha szabad ilyet mondani, a klasszikus fizika fogalmai kevésbé relációs jellegűek, és így közelebb állnak a hagyományos logika és a mindennapi gondolkozás szubjektum-predikátum felfogásához, míg a modern fizika felfogása erősebben relációs jellegű. Einstein az eseményeket is relációknak tekinti: "Hogyan kapjuk meg egy eseménynek a vonathoz viszonyított helyét és idejét, ha ismerjük ugyanannak az eseménynek a vasúti töltésre vonatkoztatott helyét és idejét?"¹² A példákból látszik, hogy más az alapvető mechanikai jellemzők logikai szintaxisa a speciális relativitáselméletben és más a klasszikus fizikában. Vizsgáljuk meg a kifejezések szemantikáját, jelentését is. A különbség itt is alapvető. A klasszikus fizika a hagyományos filozófiák gondolkozásmódjához hasonlóan intuitíve nyilvánvalónak tekintette, hogy mit jelent a távolság és az idő, nem így Einstein: "Ha minden súlyos aggály és behatómagyarázat nélkül a mechanika feladatát így szögezem le: »A mechanikának le kell írnia, miként változtatják a testek térbeli helyüket az időben«, akkor a világosság szelleme ellen elkövetett halálos bűnnel terhelem lelkiismeretemet: fedjük fel a bűnöket. Nem világos, mit értsünk itt »hely«-en és »térlaquo;-en."¹³ Einstein minden esetben a mérésre, megfigyelésre vezeti vissza a fizikai jellemzők jelentését, és elveti a spekulatív definíciók használatát. A fizika időfogalmáról című részben külön foglalkozik ezzel a kérdéssel: "Valamely fogalom a fizikus számára csak akkor létezik, ha megvan annak a lehetősége, hogy adott esetben megállapíthassuk, vajon helyes-e a fogalom, vagy sem. Tehát az egyidejűségnek olyan definíciója szükséges, hogy vele egyszersmind módszer birtokába jussunk, amellyel a jelen esetben kísérletileg dönthessük el, vajon a két villámcsapás egyidejűleg történt-e, vagy sem. Mindaddig, míg ez a követelésünk nem teljesül, a fizikus (de a nem fizikus is!) csalódik, ha azt hiszi, hogy az egyidejűség állításának értelmet tulajdoníthat (mindaddig, míg ez meggyőződéseddé nem vált, kedves olvasóm, ne haladj tovább)."¹⁴ Novobátzky Károly külön felhívja a figyelmet: "Einstein határozottan kiemeli, hogy egy definíció a fizikus számára értéktelen, ha nem vagyunk olyan módszer birtokában, amellyel a definícióból eredő folyományokat kísérletileg ellenőrizhetjük." Nem azt mondja Einstein és Novobátzky Károly, hogy csak addig, vagy csak ott és akkor van egy merev test tömegközéppontjának helye és sebessége valamely koordináta-rendszerben, ha épp akkor mérjük, és ha nem méri valaki, akkor nincs, hanem hogy az igazolás vagy cáfolás módja és eredménye ad igazságkritériumot és jelentést. Nincs ez ellentétben a klasszikus fizika szemléletmódjával, de ott talán kevésbé fogalmazódott meg ilyen világosan. Hogy mennyire nem áll távol a relativitáselmélettől a szemantika gondolkozásmódja, mutatja az is, hogy Einstein könyvében a szemantika egyik alapfogalmával, az igazsággal is foglalkozik, sőt azzal kezdi a nagyközönségnek szánt könyvét, miképp értelmezhető a geometriai tételek igazsága.

Ha igaz, ahogy én látom, hogy a relativitáselméletben használt fizikai jellemzők mind a logikai szintaxis, mind a szemantika tekintetében eltérnek a klasszikus fizika fogalmaitól, akkor egy, a két elmélet lényegi azonosságát kimutató érvelés nem lehet helyes, és E. Szabó László ebben téved.

Excel-táblázatok működő modelljeiben összefoglaltam az eddigieket, amely letölthető az Internetről.¹⁵ Figyeljük meg, hányféle időt használunk, érzékelünk avagy látunk, miközben tanulmányozzuk a modellt. Lehetne-e a világ olyan, ahogy a klasszikus fizika írja le? Igen, ha létezne végtelen gyors távolhatás és információátadás. Milyen szerkezetű a tér-idő, kontinuum sűrűségű, melynek leírásához a valós számokra van szükségünk, vagy atomos szerkezetű? Einstein válasza egyértelműen az előbbi. Ha mégis föltételezzük, hogy a tér és idő atomos szerkezetű - azaz a leírásához elegendő lenne a diszkrét matematika, és a valós számok használata csak az egyszerű tárgyalásmód következménye -, akkor abból érdekes dolgok következnek. Egy Zénon-aporián alapuló érveléssel kimutatható, hogy a véges felbontásútér-idő felfogásból bizonyos kiegészítő feltevéssel a sebesség felső határértéke következik.

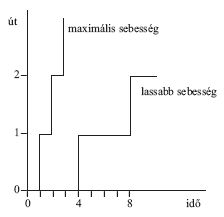
Tegyük fel, hogy m tömegpont egyenes vonal mentén A pontból B pontba halad t₁ időpontban indulva és t ₂ időpontban megérkezve. Természetes az a föltevés, hogy eközben minden időpontban van valahol, és minden időpontban egy és csak egy helyen van. Fordítva is igaz, ha a pont valahol tartózkodik, akkor ahhoz tartozik egy időpont. A vonal pontjai melyen a pont áthalad, sorba rendezettek olyan módon, hogy bármely két különböző hely közül el tudjuk dönteni, hogy melyik van közelebb a B ponthoz. A P pont mozgása során minden helyet érint A és B között, egyet sem hagy ki vagy ugrik át. A következő feltevés azonban már vitatható. A pont folyamatosan halad előre, tehát ha x időpont későbbi, mint t₁, akkor a pont x-hez tartozó helye közelebb van B-hez, mint a korábbi időpontban lévő helye. Ebből az következik, hogy a pont miközben halad, folyamatosan mozog bármely t₁ és t ₂ t2 közé eső két időpontban - t₁--et és t ₂ -t is beleértve. Amennyiben két időpont nem azonos, akkor a pont hozzá tartozó két helye is különbözik. Ha most feltételezzük, hogy a tér és az idő is atomos szerkezetű, akkor a pont t₁ és t ₂ közötti időtartam alatt csak véges sok időpont-hely koordinátaponton halad át. Belátható, hogy ebben az esetben csak egyetlen sebességgel haladhat a pont, és az éppen a legrövidebb hossz és időtartam által meghatározott maximális sebesség lesz. Tegyük fel ugyanis, hogy egy időatom alatt a pont kettő vagy több tératomot halad előre. Mivel feltételeztük, hogy a pont nem hagy ki helyet, és mindig van valahol, diszkrét időskála alapján nem tudhatjuk, hogy hol van a pont, ha egyszerre több tératomot halad egy időatom alatt. Valahol lennie kell, de feltételeztük, hogy egyszerre több helyen nem lehet. Ez viszont ellentmond annak, hogy egy időatom alatt több tératomot halad. Amennyiben viszont a pont lassabban halad, mint a maximális sebesség, akkor némelyik két szomszédos időponthoz egyazon hely tartozik, ami viszont a folyamatos haladás kikötését sérti meg. Ha ezt elvetjük, akkor a lassabb sebességeknek a pont szaggatott előrehaladása, majd a sebességtől függően hosszabb-rövidebb ideig való egyhelyben maradása fog megfelelni.¹⁶ Ekkor a pont ilyen sajátos, szaggatott módon a maximális sebességgel, vagy annál lassabban haladhat. A helyet nem determinisztikus jellemzőként, hanem valószínűségi eloszlásfüggvényként értelmezve talán a folyamatos haladásnak is tulajdoníthatunk értelmet ebben a diszkrét világban.

András Ferenc
ferenc@andrasek.hu

__________________________________________
1 E. Szabó Lászlóval a relativitáselméletről beszélgetett Balázs László Kristóf, Beszélő, 2004. január, 76. o. http://beszelo.c3.hu/04/01/10leszabo.htm. E. Szabó koncepcióját Hraskó Péter bírálja fizikus szemmel: http://www.hrasko.com/peter
2 Albert Einstein, A speciális és általános relativitás elmélete, ford. Vámos Ferenc, Gondolat, Bp. 1973, IV. kiadás. 20. o. A szöveget az eredetivel egybevetette és szakmailag ellenőrizte Károlyházi Frigyes. A könyvet Novobátzky Károly látta el magyarázó, kiegészítő jegyzetekkel.
3 i.m. 20. o.
4 i.m. 35. o.
5 i.m. 58. o.
6 i.m. 37. o.
7 Albert Einstein, Válogatott tanulmányok, Gondolat, Bp. 1971, 69.o.
8 i.m. 42. o.
9 i.m. 43. o.
10 Albert Einstein, Válogatott tanulmányok, Gondolat, Bp. 1971, 59.o.
11 i.m. 37. o.
12 i.m. 37. o.
13 i.m. 19. o.
14 i.m. 29. o.
15 http://ferenc.andrasek.hu
16 A gondolat kiinduló pontja: Ruzsa Imre, A matematika néhány filozófiai problémájáról, Tankönyvkiadó, Budapest, 1966, 65-66 o.