Syed M. Qaim1, Sudár Sándor1,2, Andreas Fessler1,3
1Institut für Nuklearchemie, Forschungszentrum Jülich, Németország
2Kísérleti Fizika Tanszék, Debreceni Egyetem
3Institute for Reference Materials and Measurements, Geel, Belgium
 p),
és az ezekből származó izomér hatáskeresztmetszet-
arányok összehasonlítása egyszerűbb reakciókéval,
mint (p,n) stb. Az eredmények rávilágíthatnak
a reakciócsatornának az izomér hatáskeresztmetszetarányra
gyakorolt esetleges hatására. Mi a 52m,gMn izomérpár
vizsgálatát választottuk 52Cr(p,n), 52Cr(3He,t), 54Fe(d,
p),
és az ezekből származó izomér hatáskeresztmetszet-
arányok összehasonlítása egyszerűbb reakciókéval,
mint (p,n) stb. Az eredmények rávilágíthatnak
a reakciócsatornának az izomér hatáskeresztmetszetarányra
gyakorolt esetleges hatására. Mi a 52m,gMn izomérpár
vizsgálatát választottuk 52Cr(p,n), 52Cr(3He,t), 54Fe(d, ),
54Fe(n,t) és 54Fe(3He,
),
54Fe(n,t) és 54Fe(3He, p) reakciókban. A metastabil állapot
spinje 2+ az alapállapoté pedig 6+. Mindkettő elektronbefogással
és pozitronbomlással is bomlik, a metastabil állapot
csaknem függetlenül, 52Cr-ra. Minden mérést radiokémiai
módszerekkel végeztünk. A reakciómechanizmus
megértése érdekében magmodellszámításokat végeztünk
a nemrég kifejlesztett EMPIRE-II kóddal.
p) reakciókban. A metastabil állapot
spinje 2+ az alapállapoté pedig 6+. Mindkettő elektronbefogással
és pozitronbomlással is bomlik, a metastabil állapot
csaknem függetlenül, 52Cr-ra. Minden mérést radiokémiai
módszerekkel végeztünk. A reakciómechanizmus
megértése érdekében magmodellszámításokat végeztünk
a nemrég kifejlesztett EMPIRE-II kóddal.
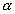 )52m,gMn mérések részleteit máshol közöljük
[7-9]. A 54Fe(3He,
)52m,gMn mérések részleteit máshol közöljük
[7-9]. A 54Fe(3He,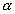 p)52m,gMn folyamatot a korábbiakhoz
[7-9] hasonló technikával vizsgáltuk, és az eredményeket
[10] ismerteti.
A 54Fe(n,t)52m,gMn reakcióra vonatkozó mérésekhez
három neutronforrást használtunk: a) d/t neutrongenerátor
Jülichben [11], b) d/t neutronforrás a geeli Van de
Graaff generátornál [10], c) d/Be breakup neutronforrás
Jülichben a JULIC közepes energiájú ciklotron mellett
[12]. Minden esetben aktivációs technikát használtunk. E
mérések részleteit korábban már közöltük [10-12].
Minthogy a két érintett izomér állapotra vonatkozó
hatáskeresztmetszetek független kísérletekből származnak,
az izomér hatáskeresztmetszet-arányokra vonatkozó
teljes mérési bizonytalanságok valamivel nagyobbak,
mint az egyes hatáskeresztmetszeteké. A töltött részecskés
reakciókból származó hatáskeresztmetszet-arányok
bizonytalanságait 16-18%-ra becsüljük, míg a neutronos
mérésekből származókat 25-30%-ra.
p)52m,gMn folyamatot a korábbiakhoz
[7-9] hasonló technikával vizsgáltuk, és az eredményeket
[10] ismerteti.
A 54Fe(n,t)52m,gMn reakcióra vonatkozó mérésekhez
három neutronforrást használtunk: a) d/t neutrongenerátor
Jülichben [11], b) d/t neutronforrás a geeli Van de
Graaff generátornál [10], c) d/Be breakup neutronforrás
Jülichben a JULIC közepes energiájú ciklotron mellett
[12]. Minden esetben aktivációs technikát használtunk. E
mérések részleteit korábban már közöltük [10-12].
Minthogy a két érintett izomér állapotra vonatkozó
hatáskeresztmetszetek független kísérletekből származnak,
az izomér hatáskeresztmetszet-arányokra vonatkozó
teljes mérési bizonytalanságok valamivel nagyobbak,
mint az egyes hatáskeresztmetszeteké. A töltött részecskés
reakciókból származó hatáskeresztmetszet-arányok
bizonytalanságait 16-18%-ra becsüljük, míg a neutronos
mérésekből származókat 25-30%-ra.
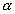 )52m,gMn,
54Fe(n,t)52m,gMn and
54Fe(3He,
)52m,gMn,
54Fe(n,t)52m,gMn and
54Fe(3He,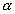 p)52m,gMn reakciókra. Ez a kód a statisztikus
részre a Hauser-Feshbach-modellt használja (beleértve a
szélességek fluktuációjának korrekcióját [HRTW]), és az
excitonmodellt a magreakció precompound részére. A
standard könyvtárat használtuk a bementi paraméterek
megadására; ez tartalmazta az atommagtömegeket, az
alapállapoti deformációkat, a különálló nívókat és a
bomlási sémákat, nívósűrűségeket, tehetetlenségi nyomatékokat
(MOMFIT) és a gamma-sugárzások gerjesztési
függvényeit.
A részecsketranszmissziós együtthatókat - mind az
exciton-, mind a Hauser-Feshbach-formalizmus számára
- gömbszimmetrikus optikai modellel, a SCAT 2 [14, 15]
számítógépes kóddal állítottuk elő. A számításokhoz
szükséges globális paramétereket neutronokra és protonokra
Koning és Delaroche [16], míg az alfa-részecskék
számára McFadden és Satchler [17] munkáiból vettük. A
54Fe(3He,
p)52m,gMn reakciókra. Ez a kód a statisztikus
részre a Hauser-Feshbach-modellt használja (beleértve a
szélességek fluktuációjának korrekcióját [HRTW]), és az
excitonmodellt a magreakció precompound részére. A
standard könyvtárat használtuk a bementi paraméterek
megadására; ez tartalmazta az atommagtömegeket, az
alapállapoti deformációkat, a különálló nívókat és a
bomlási sémákat, nívósűrűségeket, tehetetlenségi nyomatékokat
(MOMFIT) és a gamma-sugárzások gerjesztési
függvényeit.
A részecsketranszmissziós együtthatókat - mind az
exciton-, mind a Hauser-Feshbach-formalizmus számára
- gömbszimmetrikus optikai modellel, a SCAT 2 [14, 15]
számítógépes kóddal állítottuk elő. A számításokhoz
szükséges globális paramétereket neutronokra és protonokra
Koning és Delaroche [16], míg az alfa-részecskék
számára McFadden és Satchler [17] munkáiból vettük. A
54Fe(3He,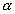 p)52m,gMn,
54Fe(d,
p)52m,gMn,
54Fe(d,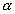 )52m,gMn, 54Fe(n,t)52m,gMn és a
52Cr(3He,t+dn)52m,gMn reakcióknál csak a Hauser-Feshbach
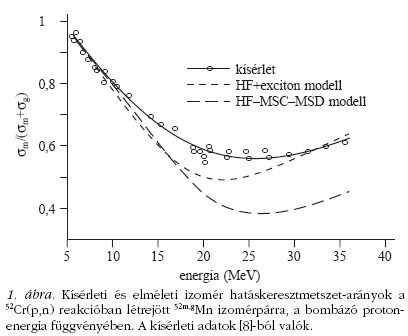
(HF) modellel végeztünk számításokat. A 52Cr(p,n)52m,gMn
reakció esetén azonban egyrészt a HF-MSC-MSD modell
mellett a HF-DEGAS excitonmodellt [18] is használtuk,
impulzusmomentum-megmaradással és gamma-bomlásokkal.
A nívósűrűségeket a kritikus gerjesztési energiák
alatt az EMPIRE-II dinamikus módszerével számítottuk ki
a szuperfolyékony modell (BSC) formalizmusával, a kritikus
energia felett pedig a Fermi-gáz-modellel. Sajnos az
EMPIRE kód az egymást megelőző folyamatokat csak a
neutron- és a protoncsatornákban tudta kezelni.
)52m,gMn, 54Fe(n,t)52m,gMn és a
52Cr(3He,t+dn)52m,gMn reakcióknál csak a Hauser-Feshbach
(HF) modellel végeztünk számításokat. A 52Cr(p,n)52m,gMn
reakció esetén azonban egyrészt a HF-MSC-MSD modell
mellett a HF-DEGAS excitonmodellt [18] is használtuk,
impulzusmomentum-megmaradással és gamma-bomlásokkal.
A nívósűrűségeket a kritikus gerjesztési energiák
alatt az EMPIRE-II dinamikus módszerével számítottuk ki
a szuperfolyékony modell (BSC) formalizmusával, a kritikus
energia felett pedig a Fermi-gáz-modellel. Sajnos az
EMPIRE kód az egymást megelőző folyamatokat csak a
neutron- és a protoncsatornákban tudta kezelni.
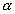 )52m,gMn
reakciónál a számított értékek valamivel
alacsonyabbak, a 54Fe(3He,
)52m,gMn
reakciónál a számított értékek valamivel
alacsonyabbak, a 54Fe(3He,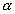 p)52m,gMn
reakciónál pedig
jelentősen alacsonyabbak, mint a kísérleti értékek, jóllehet
a kísérleti és az elméleti görbék alakja nagyon hasonló
(2. és 3. ábra). Ezek az eredmények azt mutatják,
hogy a HF-módszer egyedül (azaz elhanyagolva a precompound
részt) alulbecsüli a 2+ gerjesztett állapot járulékát
a 6+ alapállapotéhoz viszonyítva. Az 54Fe(n,t)52m,gMn
reakciónál a számított értékek többé-kevésbé összhangban
vannak a kísérleti adatokkal 19 és 23 MeV között,
azonban jelentősen eltérnek attól a reakcióküszöb közelében
(4. ábra). Nyilvánvalóan az alacsonyabb impulzusmomentumú
izomér járulékát drasztikusan alulbecsüli ez
a módszer a reakcióküszöb közelében. Ugyancsak a
52Cr(3He,t)52m,gMn folyamatra számított adatok igen érdekesen
viselkednek: jó egyezés van a kísérleti adatokkal
körülbelül 15 MeV-ig, ám efölött az elméleti adatok hirtelen
lecsökkennek, és a kísérleti adatok alatt maradnak a
vizsgált energiatartomány végéig (5. ábra ). Ez a reakció
azonban különleges, hiszen itt egyrészt direkt töltéscserélő
folyamatok, másrészt t-, dn-, p2n-, 2np-, illetve npnrészecskéket
kibocsátó folyamatok is végbemehetnek.
A fentiekből leszűrhető, hogy az elmélet csak egyszerű
nukleonemissziós reakcióknál tudja jól leírni az izomér
hatáskeresztmetszeteket nagy energiatartományban. Bonyolultabb
reakcióknál az elmélet és a kísérleti adatok között
viszonylag nagy eltérés van. Ez utóbbi esetben valószínűleg
a direkt reakcióknak nagy járuléka lehet, ezeket viszont
a statisztikus számítások nem veszik figyelembe.
Az 1-5. ábrán látható kísérleti adatok a részt vevő állapotok
impulzusmomentumának (spinjének) fontosságát is
megerősítik. Az alacsonyabb impulzusmomentumú izomér
állapot hatáskeresztmetszete növekvő bombázó energiával
jobban csökken, mint a magasabb spinű alapállapoté.
p)52m,gMn
reakciónál pedig
jelentősen alacsonyabbak, mint a kísérleti értékek, jóllehet
a kísérleti és az elméleti görbék alakja nagyon hasonló
(2. és 3. ábra). Ezek az eredmények azt mutatják,
hogy a HF-módszer egyedül (azaz elhanyagolva a precompound
részt) alulbecsüli a 2+ gerjesztett állapot járulékát
a 6+ alapállapotéhoz viszonyítva. Az 54Fe(n,t)52m,gMn
reakciónál a számított értékek többé-kevésbé összhangban
vannak a kísérleti adatokkal 19 és 23 MeV között,
azonban jelentősen eltérnek attól a reakcióküszöb közelében
(4. ábra). Nyilvánvalóan az alacsonyabb impulzusmomentumú
izomér járulékát drasztikusan alulbecsüli ez
a módszer a reakcióküszöb közelében. Ugyancsak a
52Cr(3He,t)52m,gMn folyamatra számított adatok igen érdekesen
viselkednek: jó egyezés van a kísérleti adatokkal
körülbelül 15 MeV-ig, ám efölött az elméleti adatok hirtelen
lecsökkennek, és a kísérleti adatok alatt maradnak a
vizsgált energiatartomány végéig (5. ábra ). Ez a reakció
azonban különleges, hiszen itt egyrészt direkt töltéscserélő
folyamatok, másrészt t-, dn-, p2n-, 2np-, illetve npnrészecskéket
kibocsátó folyamatok is végbemehetnek.
A fentiekből leszűrhető, hogy az elmélet csak egyszerű
nukleonemissziós reakcióknál tudja jól leírni az izomér
hatáskeresztmetszeteket nagy energiatartományban. Bonyolultabb
reakcióknál az elmélet és a kísérleti adatok között
viszonylag nagy eltérés van. Ez utóbbi esetben valószínűleg
a direkt reakcióknak nagy járuléka lehet, ezeket viszont
a statisztikus számítások nem veszik figyelembe.
Az 1-5. ábrán látható kísérleti adatok a részt vevő állapotok
impulzusmomentumának (spinjének) fontosságát is
megerősítik. Az alacsonyabb impulzusmomentumú izomér
állapot hatáskeresztmetszete növekvő bombázó energiával
jobban csökken, mint a magasabb spinű alapállapoté.
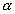 ), (n,t) és
(3He,
), (n,t) és
(3He,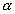 p) reakciókra (C, D és E
görbék). Az izomér hatáskeresztmetszet-arányok abszolút
értékei azonban jelentősen eltérnek. A megfigyelt trendből
arra lehet következtetni, hogy a reakciócsatorna jelentősen
befolyásolja az izomér hatáskeresztmetszetarányt,
különösen akkor, ha a reakciócsatornák nagyon
különbözőek: például (p,n) és (3He,t) folyamatok.
Köszönetnyilvánítás
Köszönjük H.H. Coenennek e munka támogatását, valamint a jülichi
kompakt ciklotron és a geeli Van de Graaff gyorsítómunkatársainak a
besugárzások elvégzését.
Irodalom
p) reakciókra (C, D és E
görbék). Az izomér hatáskeresztmetszet-arányok abszolút
értékei azonban jelentősen eltérnek. A megfigyelt trendből
arra lehet következtetni, hogy a reakciócsatorna jelentősen
befolyásolja az izomér hatáskeresztmetszetarányt,
különösen akkor, ha a reakciócsatornák nagyon
különbözőek: például (p,n) és (3He,t) folyamatok.
Köszönetnyilvánítás
Köszönjük H.H. Coenennek e munka támogatását, valamint a jülichi
kompakt ciklotron és a geeli Van de Graaff gyorsítómunkatársainak a
besugárzások elvégzését.
Irodalom
 -particle induced
reactions in the energy region up to 25 MeV - Phys. Rev. C53
(1996) 2885
-particle induced
reactions in the energy region up to 25 MeV - Phys. Rev. C53
(1996) 2885
 and 94,95Mo+p - Phys. Rev. C56 (1997) 2654
and 94,95Mo+p - Phys. Rev. C56 (1997) 2654
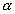 )
and (n,2n) reactions from 6 to 15 MeV - Phys. Rev. C52 (1995)
2546
)
and (n,2n) reactions from 6 to 15 MeV - Phys. Rev. C52 (1995)
2546