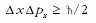
Fizikai Szemle honlap |
Tartalomjegyzék |
Lovas István
professor emeritus, Debrecen
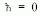 esetben visszakapjuk a klasszikus mechanika
Newton-féle elméletét. Ez pedagógiailag rendkívül fontos
eredmény! Azt bizonyítja ugyanis, hogy a Newton-mechanika
"jó", nem kell elvetni! A kvantummechanika a
klasszikus mechanikának csupán az érvényességi határát
jelöli ki a mikrovilág irányában.
Nézzük ezután a relativisztikus mechanikát! A legtöbb
tankönyv ugyancsak tartalmazza annak bizonyítását,
hogy a
esetben visszakapjuk a klasszikus mechanika
Newton-féle elméletét. Ez pedagógiailag rendkívül fontos
eredmény! Azt bizonyítja ugyanis, hogy a Newton-mechanika
"jó", nem kell elvetni! A kvantummechanika a
klasszikus mechanikának csupán az érvényességi határát
jelöli ki a mikrovilág irányában.
Nézzük ezután a relativisztikus mechanikát! A legtöbb
tankönyv ugyancsak tartalmazza annak bizonyítását,
hogy a 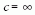 esetben visszakapjuk a klasszikus
mechanika
Newton-féle elméletét. Ez pedagógiailag ugyanolyan
fontos eredmény, mint az előző! Arra világít rá, hogy a
Newton-féle mechanika "jó"! Korrekcióra csak akkor szorul,
ha a mozgás sebessége megközelíti a fénysebességet.
Az itt idézett két, széles körben ismert, pedagógiailag
nagyon fontos tényt sokszor úgy értelmezik, hogy ha a
Planck-állandó helyébe zérust, a fénysebesség helyébe
viszont végtelent helyettesítenénk, akkor visszakapnánk
azt az emberszabású "klasszikus világot", amelyben mi,
emberek otthon érezzük magunkat.
Ez azonban tévedés! Az alábbiakban ezt kívánjuk bebizonyítani.
Nézzük először a sokrészecskés kvantummechanikát.
Közismert, hogy egy részecske x helykoordinátájához
szükségképpen hozzátartozik egy
esetben visszakapjuk a klasszikus
mechanika
Newton-féle elméletét. Ez pedagógiailag ugyanolyan
fontos eredmény, mint az előző! Arra világít rá, hogy a
Newton-féle mechanika "jó"! Korrekcióra csak akkor szorul,
ha a mozgás sebessége megközelíti a fénysebességet.
Az itt idézett két, széles körben ismert, pedagógiailag
nagyon fontos tényt sokszor úgy értelmezik, hogy ha a
Planck-állandó helyébe zérust, a fénysebesség helyébe
viszont végtelent helyettesítenénk, akkor visszakapnánk
azt az emberszabású "klasszikus világot", amelyben mi,
emberek otthon érezzük magunkat.
Ez azonban tévedés! Az alábbiakban ezt kívánjuk bebizonyítani.
Nézzük először a sokrészecskés kvantummechanikát.
Közismert, hogy egy részecske x helykoordinátájához
szükségképpen hozzátartozik egy 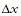 helybizonytalanság,
és hasonlóképpen a px impulzuskomponenshez egy
helybizonytalanság,
és hasonlóképpen a px impulzuskomponenshez egy 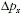 impulzusbizonytalanság. A kvantummechanika egyik alaptörvénye
kimondja, hogy a két bizonytalanságra érvényes a
impulzusbizonytalanság. A kvantummechanika egyik alaptörvénye
kimondja, hogy a két bizonytalanságra érvényes a
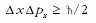
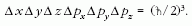
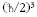 térfogatú
tartományban helyezkedik el. Ha a szóban forgó
részecske 1/2 spinű fermion, akkor érvényes rá a Pauli-féle
kizárási elv, amely kimondja, hogy egy jól definiált
kvantumállapotban legfeljebb egy részecske foglalhat helyet.
Az 1/2 spinű részecskének összesen 2 különböző spinállapota
van. N darab fermion esetén tehát fennáll az
térfogatú
tartományban helyezkedik el. Ha a szóban forgó
részecske 1/2 spinű fermion, akkor érvényes rá a Pauli-féle
kizárási elv, amely kimondja, hogy egy jól definiált
kvantumállapotban legfeljebb egy részecske foglalhat helyet.
Az 1/2 spinű részecskének összesen 2 különböző spinállapota
van. N darab fermion esetén tehát fennáll az
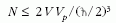
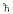 helyébe
zérust helyettesítünk? A választ az utolsó képletből
olvashatjuk le. Tetszőlegesen kicsiny V térfogatban tetszőlegesen
nagy N számú részecske "fér el". Ez azt jelenti,
hogy a fermionok elveszítik az építőkő szerepet. Nem
lehet belőlük sem molekulát, sem atomot, sem atommagot
építeni, következésképen Déva várát sem. A részecskékből
nem lehet térbeli struktúrát létrehozni.
Nézzük most az elektrodinamikát! Amint az közismert,
a Maxwell által megfogalmazott "klasszikus" elektrodinamika
azonos a relativisztikus elektrodinamikával. Elég
tehát a Maxwell-egyenletekre hivatkozni. Ha c helyébe
végtelent helyettesítünk, akkor az elektrodinamika
egyenletei szétesnek az elektrosztatika és a magnetosztatika
független egyenleteire. Ezeknek az egyenleteknek
nincsenek időfüggő megoldásai. Ezek szerint az eseményeket,
ha eseményekről egyáltalán lehetne beszélni,
nem lehet idő szerint rendezni. Közérthetően fogalmazva:
nincs történelem.
Összefoglalva megállapíthatjuk tehát, hogy, ha
helyébe
zérust helyettesítünk? A választ az utolsó képletből
olvashatjuk le. Tetszőlegesen kicsiny V térfogatban tetszőlegesen
nagy N számú részecske "fér el". Ez azt jelenti,
hogy a fermionok elveszítik az építőkő szerepet. Nem
lehet belőlük sem molekulát, sem atomot, sem atommagot
építeni, következésképen Déva várát sem. A részecskékből
nem lehet térbeli struktúrát létrehozni.
Nézzük most az elektrodinamikát! Amint az közismert,
a Maxwell által megfogalmazott "klasszikus" elektrodinamika
azonos a relativisztikus elektrodinamikával. Elég
tehát a Maxwell-egyenletekre hivatkozni. Ha c helyébe
végtelent helyettesítünk, akkor az elektrodinamika
egyenletei szétesnek az elektrosztatika és a magnetosztatika
független egyenleteire. Ezeknek az egyenleteknek
nincsenek időfüggő megoldásai. Ezek szerint az eseményeket,
ha eseményekről egyáltalán lehetne beszélni,
nem lehet idő szerint rendezni. Közérthetően fogalmazva:
nincs történelem.
Összefoglalva megállapíthatjuk tehát, hogy, ha 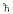 zérus lenne c pedig végtelen, akkor struktúra nem jöhetne
létre sem térben, sem időben. Az ilyen világ tehát
nem lenne az az emberszabású Világ, amelyben azért
vagyunk, "hogy valahol otthon legyünk", ahogy azt Tamási
Áron mondta.
Kelt Debrecenben, a Fizika Nemzetközi Évének végén.
zérus lenne c pedig végtelen, akkor struktúra nem jöhetne
létre sem térben, sem időben. Az ilyen világ tehát
nem lenne az az emberszabású Világ, amelyben azért
vagyunk, "hogy valahol otthon legyünk", ahogy azt Tamási
Áron mondta.
Kelt Debrecenben, a Fizika Nemzetközi Évének végén.