Fizikai Szemle honlap

Tartalomjegyzék

Fizikai Szemle 2006/10. 325.o.

KOHERENS ÁLLAPOTOK A KVANTUMOPTIKÁBAN

Ádám Péter, Janszky József
MTA SZFKI, PTE TTK Fizikai Intézet

Roy J. Glauber 2005-ben Nobel-díjat kapott az optikai koherencia kvantumelméletének és a koherens állapot reprezentációnak a kidolgozásáért. Ezeket az eredményeket 1963-ban több cikkben közölte [1, 2]. Különös érdeme, hogy rámutatott: olyan optikai jelenségek, problémák tárgyalására, ahol a fény kettős, hullám-részecske természete megnyilvánul, a kvantumelektrodinamikai leírást kell alkalmazni. Ezért Glaubert méltán tekinthetjük a kvantumoptikai kutatások elindítójának. Eredményei alapozzák meg ezt az elmúlt évtizedben rendkívül sikeres, jelentős gyakorlati eredményeket is hozó kutatási területet. Jelen írásunkban Glauber eredményeinek és a koherens állapotok jellemzőinek rövid áttekintése mellett néhány olyan kvantumoptikai eredményt mutatunk be, amelyek közvetlenül kapcsolódnak a koherens állapotokhoz, illetve a Glauber által bevezetett reprezentációhoz.

A koherens állapot

A fény kettős természetének értelmezése a 20. század elején a fizika egyik legizgalmasabb kérdése volt. A fény a terjedésénél észlelt minden jelenség során hullámként viselkedik. Ezeket a jelenségeket Maxwell elektromágneses elméletével, illetve a hullámoptika egyenleteivel tökéletesen leírhatjuk. A fény elnyelődése, kibocsátása azonban a tapasztalat szerint "adagokban" történik, a fény ilyenkor részecskeként viselkedik. 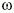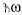Einstein 1905-ben vetette fel, hogy az keplet körfrekvenciájú fény keplet energiájú csomagokból áll. Ezeket később fotonoknak nevezték el. A fény kettős természetét egységesen tárgyaló elmélet alapja azonban csak az 1920-as évek végén, Dirac munkája nyomán született meg. Ezen elmélet szerint a sugárzási teret a klasszikus elektrodinamika törvényeinek megfelelően egy adott térrészben módusokra bontjuk, például adott polarizációjú és frekvenciájú síkhullámokra. Minden módushoz egy harmonikus oszcillátort rendelhetünk úgy, hogy az oszcillátor energiája megegyezzen a térmódus energiájával. Az oszcillátort ezután kvantáljuk, azaz a kvantummechanika elmélete szerint tárgyaljuk. Ennek megfelelően a tér normál módusainak energiaspektruma diszkrét és egyenközű. Ha a módus az n-edik sajátállapotban van, akkor azt mondjuk, hogy a módusban n foton van. A fotonszám tehát a módus gerjesztettségének a mértéke. Az n-fotonos állapot jelölésére az | n > szimbólumot használjuk. A kvantummechanikai tárgyalásnak megfelelően a fizikai mennyiségeknek operátorok felelnek meg. 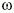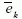Példaként tekintsük egyetlen, keplet k körfrekvenciájú, k hullámszámvektorú, keplet polarizációjú síkhullámmódus esetén az elektromos térerősség operátorát, amely egy pozitív és egy negatív frekvenciás tagra bontható:

keplet

Láthatjuk, hogy a kvantumelektrodinamikai leírásban a hullámtulajdonságok az exponenciális tagokban megőrződnek, de megjelennek a foton elnyelődését leíró keplet eltüntető és keplet keltő operátorok. Az eltüntető operátor egy fotonnal csökkenti a tér gerjesztettségét:

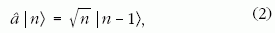
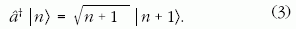
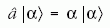
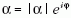keplet

a keltő operátor pedig egy fotonnal növeli azt:

keplet

Glauber egyik korszakalkotó eredménye, hogy a kvantumelektrodinamikát alkalmazta a fotondetektálás leírására, valamint a fotonkorrelációs interferenciakísérletek értelmezésére. A fény koherenciatulajdonságainak jellemzésére bevezette a kvantumkoherencia-függvényeket, amelyek a megfelelő tér- és időpillanatban vett pozitív és negatív frekvenciás térerősség-operátorok normálrendezett átlagértékei a sugárzási tér adott állapotában. A normálrendezés azt jelenti, hogy a negatív frekvenciás térerősség-operátoroka pozitív frekvenciás térerősségoperátoroktól balra állnak. A fotondetektálás valószínűsége a tér egy adott pontjabeli intenzitás átlagértékével, amit az úgynevezett elsőrendű koherenciafüggvény

keplet

ír le, arányos. Egy fotonkoincidencia-kísérlet értelmezéséhez - ilyen például a már 1956-ban elvégzett nevezetes Hanbury-Brown-Twiss-kísérlet - másodrendű koherenciafüggvényre van szükség:

keplet

Általánosan a tér 2n különböző pontja és időpillanata között a korrelációt egy n-edrendű koherenciafüggvény fejezi ki, amely n negatív és n pozitív frekvenciás térerősség- operátor szorzatának átlagértéke.

A koherenciafüggvények segítségével definiálhatjuk a sugárzási tér koherens állapotát. Az ilyen állapotú fény teljesen összefüggő, bármely rendű interferenciára képes. A tér bármely pontjában vett, bármely rendű normált koherenciafüggvény maximális értékű. Glauber megmutatta, hogy matematikailag az ilyen állapot az eltüntető operátor sajátállapota, tehát az

keplet

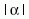egyenletet elégíti ki, ahol keplet komplex paraméter. Ezt a kvantumállapotot a harmonikus oszcillátor kvantumelméletéből ismerhetjük. A koherens állapot az oszcillátor klasszikus mozgásának megfelelő kvantumállapot. Fény esetében a példaként tekintett módusfelbontás esetén ez a monokromatikus síkhullámnak felel meg. 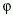A koherens állapot komplex paraméterének abszolút értéke keplet arányos a hullám amplitúdójával, keplet fázisa a hullám kezdőfázisa. A kvantumos tárgyalásból következően azonban az elektromos térerősségnek bizonytalansága van, amely fázisfüggetlen és értéke állandó, megegyezik a vákuumzajjal. A koherens állapotú fény így növekvő gerjesztettség mellett egyre jobban megfelel a klasszikus hullámnak, hiszen a kvantumzaja elhanyagolható lesz az amplitúdójához képest. Érdemes megemlíteni, hogy egy ideális lézer koherens állapotú fényt bocsát ki. Glauber elméleti eredményeit, kétségkívül, az első lézereknek a '60-as évek elején történt kifejlesztése is motiválta.

A koherens fény nevezetes jellemzője, hogy fotonstatisztikája, tehát az n-fotonos állapotok eloszlása Poisson-eloszlás, azaz

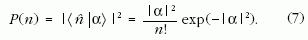
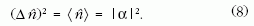
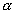keplet

A fotonszám középértéke és szórásnégyzete megegyezik és egyenlő az amplitúdó abszolút értékének négyzetével.

1. ábra

keplet

Koherens fény esetén a fotondetektálási események teljesen függetlenek egymástól, köztük semmilyen korreláció nincsen. Tehát ez a fény nem mutatja sem a fotoncsomósodás (bunching), sem a fotonritkulás (anti-bunching) jelenségét, az egyes események közt eltelt időintervallumok exponenciális eloszlásúak. A fotonszámeloszlás egy fotodetektálási kísérletben az adott időintervallumban beérkezett fotonok számának valószínűségeloszlásából határozható meg.

Glauber másikjelentős eredménye annak felismerése, hogy koherens állapotok segítségével a fény tetszőleges kvantumállapota reprezentálható. Korábban rendszerint a fotonszám állapotok, tehát az energia-sajátállapotok által alkotott bázist használták kvantumelektrodinamikai számításokhoz. A koherens állapot reprezentációt az teszi lehetővé, hogy bár két koherens állapot nem ortogonális egymásra, a koherens állapotok teljes bázist alkotnak az adott módust leíró harmonikus oszcillátor állapotterében. A reprezentációt szemléletessé teszi, hogy a koherens állapotok keplet paramétere által meghatározott komplex sík megfelel a kvantummechanikai fázistérnek. Ennek koordinátatengelyeit fény esetében az úgynevezett 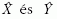keplet kvadratúraoperátorok átlagértékei adják. Ezekkel az operátorokkal a tér rezgéseit a klasszikus eljárásnak megfelelően két, keplet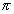/2 fáziskülönbségű, egymásra merőlegesen oszcilláló mennyiségre bontjuk. A kvantummechanikai leírásban a két kvadratúraoperátor kanonikusan konjugált, tehát a kvadratúrák nem mérhetők egyszerre, szórásaikra teljesül a

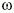keplet

Heisenberg-féle határozatlansági reláció. Az 1. ábrán a koherens állapotnak megfelelő pontot a kvantummechanikai bizonytalanságot is mutató körrel ábrázoltuk a fázistérben. A dimenziótlan kvadratúramennyiségek bizonytalansága egyenlő nagyságú és minimális, azaz a Heisenberg-féle határozatlansági összefüggés egyenlőségként teljesül. A koherens állapotnak megfelelő pont az időbeli fejlődés során keplet körfrekvenciával forog a fázistér origója körül.

A fázistéren értelmezhetünk úgynevezett kvázivalószínűség- eloszlásfüggvényeket, a klasszikus statisztikus fizika fázistérbeli eloszlásfüggvényeihez hasonlóan. (Ilyen például a Wigner Jenő által 1932-ben bevezetett Wigner-függvény.) Ezekkel a fény kevert állapotait is jellemezhetjük, amelyek nem írhatók le egyetlen állapotvektorral. Az egyik legjellegzetesebb példa kevert állapotra a termikus állapot, amely egy termikus fényforrás, például egy egyszerű izzólámpa fényét írja le. 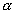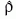Glauber a kevert állapotokat leíró sűrűségoperátor reprezentálására a P(keplet) kvázivalószínűség-eloszlást vezette be, amellyel egy kevert kvantumállapot sűrűségoperátora a következő keplet diagonális alakba írható:

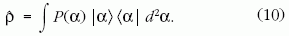
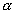keplet

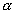A sűrűségoperátor tehát a koherens állapotokra vetítő projektor-operátorok a teljes fázistéren P(keplet) súlyfüggvénnyel vett keveréke. A Glauber-féle P-függvény bizonyos problémák tárgyalásakor matematikailag előnyösebb tulajdonságokkal rendelkezik, mint más kvázivalószínűség- eloszlásfüggvények.

Glauber megmutatta azt is, hogy a kvantummechanikai eloszlásfüggvények nem tekinthetők a klasszikus eloszlásfüggvények egyértelmű megfelelőjének. Ezek a függvények a klasszikus megfelelő nélküli kvantumállapotokban ugyanis negatív értéket is felvehetnek. A lézerek megjelenése előtt csak termikus fényforrásokat ismertünk. A termikus fény P(keplet) függvénye Gauss-függvény, ezért alkalmazható a vele végzett kísérletek értelmezésére a klasszikus fluktuációelmélet. Természetesen a koherens fénnyel végzett kísérletek is értelmezhetőek a klasszikus elmélettel. Érthető módon a Glauber eredményeit követően megindult kvantumoptikai kutatások egyik fő célja a fény nevezetes nemklasszikus állapotainak megtalálása, leírása és előállítása volt.

A fény nemklasszikus állapotai

A fénynek végtelen sok kvantumállapota létezhet. A fény kvantumállapota általában megváltozik, ha valamilyen optikai folyamatban vesz részt. Megváltozik az állapota akkor is, ha detektáljuk, hiszen fotonok abszorbeálódnak a térből. Egy tiszta kvantumállapotú fény kevert állapotúvá válik, ha csillapodási folyamatban vesz részt. A csillapodás alapesete egy részlegesen áteresztő tükrön való áthaladás. Valójában csak a koherens állapotú és a termikus fény tekinthető klasszikusnak. Ezek kvantumállapota a csillapodási folyamatban sem változik, csak intenzitásuk csökken.

2. ábra

A fény nemklasszikus állapotai között vannak nevezetes tulajdonságúak, amelyekkel kapcsolatos kutatások már a '70-es évek elején megindultak. Legtöbb figyelmet az összenyomott (squeezed) fény kapott. Az ilyen fénynek az a jellemző tulajdonsága van, hogy valamelyik mérhető fizikai mennyiségének kvantumzaja kisebb, mint koherens állapotban. A konkrét elnevezés tartalmazza annak a fizikai mennyiségnek a megnevezését, amelynek bizonytalansága kisebb a koherens értéknél. 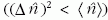Például az amplitúdó-összenyomott fény fotonszámszórása kisebb a koherens fényénél keplet, fotonszámeloszlása pedig keskenyebb, mint a Poisson-eloszlás, azaz szub- Poisson statisztikájú.

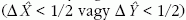Kvadratúra-összenyomott állapotban az egyik kvadratúramennyiség szórása kisebb, mint a koherens érték keplet. A Heisenberg-féle határozatlansági összefüggésnek megfelelően természetesen a másikmennyiség zaja megnő. Az ilyen állapotot egy ellipszissel ábrázolhatnánk az 1. ábrán bemutatott fázistérben. Kvadratúra-összenyomott vákuumállapotot úgynevezett optikai parametrikus oszcillátorral állíthatunk elő. 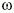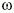Ebben az eszközben egy 2keplet frekvenciájú lézerfénnyel pumpált nemlineáris kristályban két, keplet frekvenciájú módus keletkezik. Ezek féligáteresztő tükrön történő keverése adja a kívánt állapotot, amely ideális esetben minimális bizonytalanságú állapot, azaz a Heisenberg-féle határozatlansági összefüggés egyenlőségként teljesül. Ezen kívül számos más nemlineáris optikai folyamatban is keletkezhet összenyomott fény. Koherens fényből kiindulva összenyomott koherens fényt kaphatunk, amelynek kvantumzaja fázisfüggő. Bizonyos fázispontokban csökken, másutt nő a koherens értékhez képest. Nevezetes eredmény, hogy két koherens állapot kvantummechanikai szuperpozíciója is összenyomott állapotot eredményezhet. Az ilyen állapotot szokás optikai Schrödinger- macska állapotnak is nevezni, hiszen két, makroszkopikusan megkülönböztethető kváziklasszikus állapot szuperpozíciója, amely Schrödinger híres paradoxonában is szerepel. A nemklasszikus tulajdonság kialakulásának oka a két állapot közötti kvantuminterferencia. Ez a szuperponált állapotot felépítő egyes állapotok mint valószínűségi amplitúdók között lép fel, ha fizikailag mérhető mennyiséget származtatunk. A különböző állapotokkal számolt operátor-középértékek az interferenciatagok. A 2. ábrán a páros Schrödinger-macska állapot, azaz a

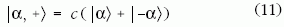
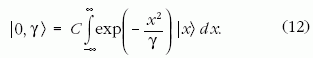
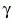keplet

állapot Wigner-függvényét láthatjuk. A 2. ábrán a két Gauss-harang a koherens állapotoknak felel meg, a hullámzó rész a kvantuminterferenciát mutatja.

Növelhetjük az összenyomottságot, ha a vákuumállapotot megfelelő súllyal hozzávesszük a szuperpozícióhoz. Ennek a felismerésnek az általánosítása vezetett el az egydimenziós koherens állapot reprezentációk bevezetéséhez. Janszky és Vinogradov 1990-ben megmutatta [3], hogy a fázistér valós egyenese mentén Gauss-súly- függvénnyel vett folytonos koherens állapot szuperpozició az összenyomott vákumállapot:

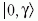keplet

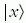Itt a keplet paraméter határozza meg a keplet összenyomott vákumállapot összenyomottságának mértékét, a keplet állapot pedig a fázistér valós tengelyén lévő koherens állapot.

3. ábra

Az ezt követő években számos nemklasszikus állapot egydimenziós koherens állapot reprezentációját sikerült megtalálni [4, 5]. A fotonszámállapotokat és az amplitúdó összenyomott állapotokat például egy origó középpontú körön vett folytonos szuperpozícióval lehet leírni. Szisztematikus eljárás is megadható bármilyen állapot egydimenziós reprezentációjának megtalálására [5]. Ezek a reprezentációk jelentősen leegyszerűsítik a számításokat a Glauber-féle, a teljes komplex síkon, azaz a teljes fázistéren vett reprezentációhoz képest. Segítségükkel az állapotok fizikai jellemzői és viselkedésük optikai folyamatokban egyszerűen elemezhetők. Igazi jelentőségük azonban az, hogy elvezettek annak felismeréséhez, hogy a fény kvantumállapotai igen jó közelítéssel előállíthatóak koherens állapotok szuperpozíciójaként [6-8]:

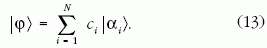
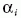keplet

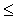A szuperpozíció az állapot egydimenziós reprezentációjának diszkretizálásával származtatható. A ci együtthatók a reprezentáció kifejtési függvényének értékei az adott keplet pontokban. A vizsgálatok kimutatták, hogy az ekvidisztans felosztás vezet a legjobb eredményre. A nevezetes állapotok többsége már kisszámú (N keplet 10) koherens állapot szuperpozíciójával előállítható [8]. Léteznek olyan diszkrét, koherensállapot-előállítások is, amelyek vákuumhoz közeli, kis amplitúdójú koherens állapotokból építik fel a kívánt állapotot. Példaként a 3. ábrán egy összenyomott koherens állapotot jelenítünk meg vizuálisan. A tüskék a szuperpozíciót alkotó koherens állapotokat reprezentálják. Magasságuk arányos az állapot ci súlyfaktorának abszolút értékével. A 3.a ábra a létrejött állapot Wigner-függvényét illusztrálja.

Ez az eredmény új lehetőséget nyitott a fény nemklasszikus állapotainak tanulmányozására. Sikerült olyan módszereket kidolgozni, amelyekkel bármilyen szuperpozíció és - egyetlen kísérleti berendezéssel, a paraméterek változtatásával - több nemklasszikus állapot is létrehozható [8, 9]. A 4. ábrán egy ilyen módszer vázlatát láthatjuk. Az elrendezésben egy kétállapotú atom halad át egy rácson és egy rezonátoron, majd a helyét detektáljuk. A rezonátorban lévő elektromágneses tér koherens állapotú, és az atomi átmenettel nem rezonáns. Megmutatható, hogy a detektálás után a rezonátorban N+1 koherens állapot körön vett szuperpozíciója alakul ki. A szuperpozíció paramétereit a rések helyének , szélességének megfelelő választásával lehet beállítani. A nemklasszikus állapotok koherens állapot szuperpozícióval történő előállítása lehetővé tette általános módszerek kifejlesztését olyan összetett optikai rendszerek tárgyalására, ahol egyszerre több lineáris és nemlineáris folyamat megy végbe [10]. A nemklasszikus állapotok fejlődése, a szuperpozíció együtthatóit ismerve, a levezetett általános összefüggésekkel egyszerűen elemezhető.

4. ábra

Napjainkig a fény számos nemklasszikus állapotát sikerült már laboratóriumokban előállítani, tulajdonságait vizsgálni és különböző kísérletekben használni. Elsősorban az optikai kommunikációban és a nagy pontosságú méréstechnikában várható, hogy a gyakorlatban is sikerül a nemklasszikus fényt felhasználni. Sajnos, a nemklasszikus tulajdonságok sérülékenysége nehezíti az alkalmazást. A környezettel történő kölcsönhatás során elkerülhetetlenül fellépő csillapodás, dekoherencia "tönkreteszi" az adott kvantumállapotot. Összenyomott állapotú fény előállítására alkalmas berendezést Magyarországon az MTA SZFKI Lézeralkalmazási Osztályán építettek. Az eszközt fotodetektorok kvantumhatásfokának mérésére használták fel [11]. Jelenleg programozható fotonszámú fényforrás fejlesztéséhez alkalmazzák.

Érdemes megemlíteni, hogy a koherens állapotokkal kapcsolatos eredmények más, harmonikus oszcillátorként tárgyalható fizikai rendszerekre is kiterjeszthetők. Nevezetes ilyen rendszert alkotnak a csapdázott ionok, amelyekkel szintén számos nemklasszikus rezgési állapot, így Schrödinger-macska állapot is előállítható. A bemutatott eredmények legújabb felhasználási területe a kvantuminformatika, amely napjaink kvantummechanikai kutatásának egyik legperspektivikusabb fejezete. E tudományterület tárgya az információtárolás és feldolgozás újszerű, kvantumjelenségeket kihasználó módszereinek kidolgozása. Az alapgondolat a következő: az információ tárolására általában valamilyen fizikai mennyiség értékét használjuk, digitális áramkörökben például egy-egy feszültségszint felel meg az adott bit 0 és 1 logikai értékének. A kvantuminformatikában az információt egy fizikai rendszer állapotában tároljuk. Egy kvantumbit lehet például egy feles spin, állapota pedig a |0> és |1> vektorok tetszőleges szuperpozíciója. Az információfeldolgozás műveleteit a kvantummechanika szabályai határozzák meg.

Ezen az elven számos olyan kommunikációs és számítási feladat elvégezhető, amelyek lehetetlenek hagyományos adatfeldolgozó eszközökkel. Például ma már lehetséges olyan titkosított optikai kommunikációs csatorna létrehozása, amelynek feltörhetetlenségét a Heisenberg-féle határozatlansági összefüggés garantálja. A kvantuminformatika egyik fontos fejezete a folytonos változós kvantuminformatika, ahol az információt fénymódusok nemklasszikus állapotaiba kódolják [12]. A koherens állapotok ebben alapvető szerepet játszanak, a szuperpozícióikkal való leírás pedig hasznos technikának bizonyult a kapcsolódó jelenségek leírásában [13, 14].

Irodalom
  1. R.J. GLAUBER - Phys. Rev. Letters 10 (1963) 84
  2. R.J. GLAUBER - Phys. Rev. 130 (1963) 2529 és 131 (1963) 2766
  3. J. JANSZKY, A.V. VINOGRADOV - Phys. Rev. Lett. 64 (1990) 2771
  4. P. ADAM, J. JANSZKY, A.V. VINOGRADOV - Opt. Commun. 80 (1990) 155 és Phys. Lett. A 160 (1991) 506
  5. P. ADAM, I. FOLDESI, J. JANSZKY - Phys. Rev. A 49 (1994) 1281
  6. J. JANSZKY, P. DOMOKOS, S. SZABO, P. ADAM - Phys. Rev. A 51 (1995) 4191
  7. P. ADAM, S. SZABO, J. JANSZKY - Phys. Lett. A 215 (1996) 229
  8. S. SZABO, P. ADAM, J. JANSZKY, P. DOMOKOS - Phys. Rev. A 53 (1996) 2698
  9. P. DOMOKOS, J. JANSZKY, P. ADAM - Phys. Rev. A 50 (1994) 3340
  10. A. KARPATI, P. ADAM, J. JANSZKY, M. BERTOLOTTI, C. SIBILIA - J. Opt. B-Quantum Semicl. Opt. 2 (2000) 133
  11. A. CZITROVSZKY, A. SERGIENKO, P. JANI, A. NAGY - Metrologia 3 (2000) 617
  12. Z. KURUCZ, P. ADAM, Z. KIS, J. JANSZKY - Phys. Rev. A 72 (2005) 052315
  13. J. JANSZKY, M. KONIORCZYK, A. GÁBRIS - Phys. Rev. A 64 (2001) 034302
  14. J.K. ASBOTH, P. ADAM, M. KONIORCZYK, J. JANSZKY - Eur. Phys. J. D 30 (2004) 403