Fizikai Szemle 2007/1. 1.o.
A 100 ÉVES EÖTVÖS-PEKÁR-FEKETE KÍSÉRLETEK ÉS MÁIG TARTÓ HATÁSUK
Király Péter
KFKI RMKI Kozmikus Fizikai Főosztály
Eötvös Loránd 1905-ben lemondott akadémiai elnöki
tisztéről, hogy a továbbiakban tudományos kutatásainak
szentelhesse idejét és erőfeszítéseit. Az ezt követő
évben három olyan fontos esemény is volt Eötvös
életében, amelyek centenáriumát akár külön-külön is
megünnepelhetnénk:
- Nemzetközi konferencián ismertette és elismertette
módszereit és eredményeit;
- Ígéretet kapott további kutatásai rendszeres,
bőkezű magyar állami támogatására;
- A Göttingeni Egyetem pályázatot írt ki, melynek
elnyeréséért kísérletekbe kezdett.
Bár Eötvös számára talán az első két esemény fontosabbnak
tűnhetett, a máig tartó hatások szempontjából
a harmadiknak volt legnagyobb jelentősége.
A Nemzetközi Földmérés (Internationale Erdmessung),
a mai International Union of Geodesy and
Geophysics szervezet (IUGG) elődje, 1906-ban Budapesten
rendezte 15. kongresszusát, amelyen Eötvös
nagy sikerű előadást tartott módszereiről, addigi eredményeiről
és az általa kifejlesztett műszerekről. Ezen
meg tudta győzni a nemzetközi szervezet vezetőit,
hogy az általa kifejlesztett "csavarási mérleg" vagy
későbbi nevén Eötvös-inga segítségével nemcsak a
Föld gravitációs nívófelületeinek helyi jellemzőit tudja
igen pontosan meghatározni, de a messze a talajszint
alatti, eltemetett hegységek jelenlétére és alakjára is
következtetni képes. Arad környékén terepi méréseken
is bemutatta módszerei hatékonyságát.
A Nemzetközi Földmérés vezérkara a hallottak és
látottak hatására azzal a kéréssel fordult a magyar kormányhoz,
hogy Eötvös nagy fontosságú munkáit hatékonyan
támogassa. A megítélt évi 60 ezer aranykoronás
támogatás, amely az Eötvös-tanszék teljes állami juttatásainak
mintegy 15-szörösét tette ki, nagyban segítette a
terepi munkákat, a műszerfejlesztést, sőt további munkatársak
alkalmazását is lehetővé tette. A támogatással
beszerzett tárgyakat a tanszék berendezésétől elkülönítve
kellett leltározni, ami az e témákkal foglalkozó
csoportnak bizonyos függetlenséget is biztosított. E
csoportból nőtt ki Eötvös halála után a hazai geofizikai
kutatásokat irányító önálló intézet, a mai Eötvös Loránd
Geofizikai Intézet (ELGI) elődje.
A Nemzetközi Földmérés szervezetének egyik alapvető
célkitűzése a Föld alakjának minél pontosabb
meghatározása volt. De mit is jelent a Föld alakja? A
tengereken az átlagos vízszint - bizonyos zavaró tényezőket
elhanyagolva - mindenhol merőleges a gravitációból
és a Föld forgása okozta centrifugáliserőből
összetevődő "nehézségi" erőre, vagyis az alakot a
nehézségi erő tengerekre simuló szintfelülete adja.
Kézenfekvő ezt a definíciót a szárazföldekre is kiterjeszteni.
Ezért beszélhetünk a szárazföld belsejében is
"tengerszint feletti magasságról".
Némi fizikusi szőrszálhasogatással felvethető azonban
az a kérdés, hogy csak a vízre, vagy minden anyagra
azonosak-e a szintfelületek. A tehetetlen és súlyos
tömeg szigorú arányossága esetén igen, de jogosan
merül föl a kérdés, hogy ha a különböző anyagokra az
arány kicsit más lenne, akkor mennyire térnének el
egymástól a szintfelületek. Eötvös először az 1880-as
évek végén, a torziós inga egy kezdeti változatával végzett
méréseket különböző anyagok tehetetlen és súlyos
tömegének arányosságára nézve. Már ekkor minden
korábbinál nagyságrendekkel pontosabban, mintegy
5x10-8 relatív hibával bizonyította a vizsgált anyagokra
az arányosságot. Ha az adott anyagokra a nehézségi
erő szintfelületeit az Egyenlítőnél egybeejtjük, akkor a
sarkoknál azok legfeljebb 0,7 mm-re térhetnének el
egymástól, vagyis földmérési (geodéziai) szempontból
teljesen kielégítő pontossággal igaz, hogy a Föld alakját
(a geoidot) függetlennek tekinthetjük attól, hogy milyen
anyagra vonatkozó szintfelülettel definiáljuk.
A pontosság elég a geodétának, de kérdés, hogy
kielégítheti-e a fizikust is. Hiszen a newtoni tömegvonzás
egyik alapvető feltevéséről van szó. Eötvös
korai kísérletei után minden bizonnyal többször
visszatért ehhez a kérdéshez, de újabb, pontosabb
vizsgálataihoz a döntő lökést a Göttingeni Egyetem
Beneke-díj pályázatának 1906-os kiírása adta. A pályázat
kiírása és a díj átadása között mindig három év
telt el. A kiírásban Eötvös kifinomult módszereire
explicite utaltak, és hangsúlyozták annak fontosságát,
hogy a kérdést a fizika időközben tett fontos felfedezéseinek
(elektrodinamika, radioaktivitás) fényében
újra megvizsgálják. A Beneke-díj bizottság elnöke
ekkor Karl Runge, a világ első alkalmazott matematika
tanszékének vezetője volt, aki numerikus matematikában
elért eredményei mellett (Runge-Kutta-
módszer) Planck barátja és a hidrogén-spektrum matematikai
leírásának szakértője is volt.
Az Eötvös-Pekár-Fekete (EPF) és
a későbbi Renner-kísérletek
A pályázat kiírása Eötvös számára minden bizonnyal
elégtételt és kihívást is jelentett. Az új kísérletsorozatban
ő már valószínűleg főleg irányítóként és konzulensként
vett részt, míg magukat a hosszadalmas méréseket
munkatársai végezték. Mivel a kora nyártól
késő őszig terjedő időszakban a kutatók minden idejét
a terepi, geodéziai és geofizikai célú mérések töltötték
ki (melyeket Pekár Dezső vezetett), a pályázattal
kapcsolatos munkák a téli és kora tavaszi időszakra
összpontosulhattak. Kivétel 1908-ban lehetett, amikor
a csak 1922-ben megjelent összefoglaló cikk [1]
tanúsága szerint a sürgető beadási határidő miatt a
kísérletek nyáron is folytatódtak. Sajnos a részletes
mérési jegyzőkönyvek elvesztek, sőt maga a benyújtott
pályázat sincs már meg, noha Selényi Pál, Eötvös
1953-ban megjelent összegyűjtött munkáinak [2] szerkesztője
még annak alapján pótolt néhány az 1922-es
cikkből kihagyott részt.
Az EPF-kísérletek alapkoncepciója ugyanaz volt,
mint Eötvös korai méréseinél. Ha a gravitációs és tehetetlenségi
erő aránya anyagfüggő, akkor különböző
anyagokra kicsit más irányú a nehézségi gyorsulás.
Egy kelet-nyugati irányban felállított, két végén két
különböző összetételű anyaggal terhelt torziós ingára
emiatt forgatónyomaték hat, amely az inga 180°-os
elforgatásakor ellenkező előjelűvé válik. Ezt a kis különbséget
kellett különválasztani a gravitációs potenciál
második deriváltjai miatt fellépő, az inga irányától
függő nyomatéktól. A korai méréseknél Eötvös rúd
alakú, először Coulomb-ingának, majd görbületi variométernek
nevezett ingát használt, amivel elég volt
két (K-Ny és Ny-K) irányban mérni. Később kifejlesztette
a ma Eötvös-ingának nevezett horizontális variométert,
amelynél az egyik oldalon lévő tömeg mélyebben
helyezkedik el, és amellyel a nehézségi potenciál
második deriváltjait sokkal részletesebben
tudta kimérni (2 helyett 4 összetevőt). Mivel az 1900-as
években a terepi mérésekhez már szinte kizárólag
horizontális variométereket használtak, az EPF-kísérleteket
is ilyenekkel végezték. A derivált tenzor összetevőit
emiatt csak akkor lehetett a mérési eredményekből
algebrailag kiküszöbölni, ha legalább négy
irányban mértek (a fentiek mellett É-D és D-É irányban
is). További komplikációt jelentett, hogy az inga
érzékenysége, valamint a környezet gravitációs hatása
(pl. esőzések vagy a pincében felhalmozott szénmennyiség
változása miatt) a hosszú méréssorozat
folyamán fokozatosan megváltozhat. Eötvös munkatársaival
három mérési módszert dolgozott ki, amelyek
e zavaró hatásokat egyre nagyobb mértékben
küszöbölték ki. Emellett a kiértékelésnél interpolációs
technikákkal igyekeztek a maradék változások hatását
minél jobban csökkenteni.
Az EPF-kísérletek végül körülbelül egy nagyságrenddel
szigorúbb felső korlátot adtak különböző
anyagpárok esetén a súlyos és tehetetlen tömeg arányának
lehetséges eltéréseire, mint Eötvös korai mérései.
Szignifikánsnak tekintett eltérést sehol sem találtak.
A Föld irányában ható nehézségi gyorsulásokon
alapuló módszer mellett végeztek egy mérést a
Nap irányában ható gyorsulások összehasonlítására
is. Ehhez az ingát É-D irányba kellett beállítani, és az
inga járásában napi periodicitást kellett keresni. Ilyen
periodicitást persze más (pl. hőmérsékleti) változások
is okozhatnak, ezért a mérést két azonos anyaggal is
el kellett végezni. Itt valamivel kisebb pontosságot
értek el, de eltérést itt sem találtak. Emellett vizsgálták,
hogy leárnyékolható-e a gravitáció, és hogy radioaktív
anyagoknál sérül-e a tehetetlen és súlyos
tömeg arányossága, mint ahogy azt egyes szerzők
állították. Mindkét esetben a várt negatív eredményre
jutottak. Az "ars longa, vita brevis" jeligéjű pályázat
benyújtása után a három szerző 1909-ben elnyerte a
Beneke-díjat. Jeligéjük arra utalt, hogy a mérések
pontossága további vizsgálatokkal még fokozható.
Az EPF-kísérletek eredményeiről először Eötvös
számolt be nyilvánosan a Nemzetközi Földmérés
1909-ben tartott 16., londoni kongresszusán. Mivel az
előadásfő témája a torziósingával végzett hazai geodéziai
vizsgálatok leírása volt, csak röviden beszélt a
nehézségi erő szintfelületeinek esetleges anyagfüggéséről.
A mérési elvek és régi mérési eredményei ismertetése
után csak megemlítette az új méréseket,
melyek pontosságaként a 10-8 értéket adta meg. Eötvös70
éves születésnapja alkalmából, 1918-ban Pekár
Dezső és Fekete Jeno írt kissé részletesebben az EPF-kísérletek
módszereiről és eredményeiről, de a részletes
beszámoló, mint már említettük, csak 1922-ben
jelent meg [1].
Renner János, aki a pályázatot követő években kapcsolódott
be a csoport munkájába, majd később a Fasori
Gimnázium nagy tekintélyű fizikatanára és igazgatója
is lett, az 1930-asévek elején jobb eszközökkel és kevésbé
feszítő időkorlátokkal lényegében megismételte
az EPF-kísérleteket (bár természetesen a vizsgált anyagpárok
és a mérések egyes részletei eltértek a korábbiaktól).
1935-ben magyar nyelven (német összefoglalóval)
közölt dolgozata [3] szerint még egy nagyságrendet
tudott javítani az EPF-kísérletek eredményén, és ennél
pontosabb eredményeket az adott módszerekkel már
nem is igen tartott lehetségesnek. A kétféle tömeg arányában
ő sem talált sehol szignifikáns eltérést.
Eötvös eredményei és
Einstein ekvivalenciaelve
Einstein 1907-ben mondta ki ekvivalenciaelvét,
amelynek alapján később az általános relativitáselmélete
ésa gravitáció geometriai interpretációja megszületett.
Az, hogy szabadon eső liftben és gravitációmentes térben
végzett nem-gravitációs kísérletek bizonyos
megszorításokkal mindig ugyanarra az eredményre
vezetnek, feltételezi a tehetetlen és súlyos
tömeg arányosságát, de annál szélesebb jelenségkörre
terjed ki. Einstein visszaemlékezései szerint az ekvivalenciaelv
megfogalmazásakor nem volt tudatában
Eötvös eredményeinek, hanem a kétféle tömeg azonossága
inkább evidenciaként, intuitív igazságként élt
tudatában. Az EPF-eredményekről már csak azért sem
tudhatott, mert azok akkor még meg sem születtek.
Elvileg azonban tudhatott volna Eötvös korai eredményeiről,
amelyek az összes addigi mérések közül
messze a legpontosabbak voltak.
Albert Einstein érdeklődése valószínűleg csak néhány
évvel később fordult az ekvivalenciaelv kísérleti
igazolása felé, amikor a gravitáció relativisztikus elméletével
kapcsolatos vitákban felmerült az a kérdés,
hogy a radioaktív bomlásnál felszabaduló energiára is
érvényes-e a tehetetlen és súlyos tömeg arányossága.
Einstein e kérdés kapcsán 1912-ben levélben fordult
Wilhelm Wienhez, a Wien-féle eltolódási törvény felfedezőjéhez
(aki 1911-ben kapott Nobel-díjat). Először
ingaméréseket javasolt uránból és ólomból készült
ingák lengésidejének összehasonlítására, és azt kérdezte,
hogy Wien szerint elérhető-e ezekkel a szükséges
pontosság. Majd új ötletként felvetette, hogy közönséges ingák
helyett torziósingával pontosabban elvégezhető
lenne a mérés, és szinte szóról szóra felvázolta a
korai Eötvös-kísérletek koncepcióját, sőt "ötletét" a
görbületi variométer vázlatos rajzával is illusztrálta [4].
Még azt is felvetette, hogy Wien ezt a fontos kísérletet
(experimentum crucis) végeztesse el laboratóriumában.
Wien e levélre adott válasza nem került elő hagyatékából.
Az viszont kétségtelen, hogy Einstein 1913-ban
Marcel Grossmannnal közösen írt cikkében már hivatkozik
a korai Eötvös-kísérletekre, azok pontosságát is
megadva. Arról, hogy e régi kísérletekre és a hivatkozott
Eötvös-cikkre Wien, Grossmann, vagy esetleg más
hívta fel figyelmét, legfeljebb találgathatunk. Az viszont
mindenképpen meglepő, hogy 1912-ben saját ötleteként
éppen Eötvös zseniális módszerét javasolta, és
felvetődhet a gyanú, hogy a méréseket valaki már korábban
is említhette neki, de erről közben elfelejtkezett.
Eötvös más irányú tevékenységéről egyébként tudott,
hiszen nem sokkal korábban közölt cikket a kapillaritás
Eötvös-törvényéről.
Einstein a potsdami geodéziai intézet igazgatójának
halála után 1917-ben tanácsot kért Eötvöstől az utódláskérdés
ében. Eötvös részletes javaslata után Einstein
viszontválaszában köszönetet mondott neki azokért
a kutatásaiért is, amelyek során a súlyos és tehetetlen
tömeg arányosságát igazolta. Emellett elküldte
neki könyvét, amelyben "e kérdéselméleti vonatkozásaival
foglalkozik".
Ekvivalenciaelv kísérletek 1960 és 1986 között
Renner János kísérletei után az 1960-as évek elejéig a
fizika szinte minden területén jelentősen fejlődött a
kísérleti technika, de a súlyos és tehetetlen tömeg
arányosságának kérdésében nem volt számottevő
előrehaladás. Maga az Eötvös-inga közben a nyersanyagkutatásban
óriási jelentőségre tett szert, és Eötvös
munkatársai (különösen Pekár Dezső és Fekete
Jenő) alaposan kivették részüket mind az inga fejlesztéséből
és exportra való gyártásából, mind a világ
különböző tájain végzett olaj- és földgázkutatás okból.
A 30-asévek végétől a gyorsabb graviméteres módszerek
nyugaton egyre inkább kiszorították a torziós
ingát a nyersanyagkutatásból, de keleten az embargó
miatt ez az átállás egészen az 50-esévekig nem történt
meg.
A 60-as években az ekvivalenciaelv első modern
módszerekkel történő ellenőrzése Robert Dicke nevéhez
fűződik, aki a gravitációelmélet, a csillagászat és
az optika területén is számos újszerű elmélettel és
technikai újítással vonta magára a figyelmet. Princetoni
csoportjával együtt alaposan felkészült a feladatra,
s ennek során a régi EPF- és Renner-mérések kritikai
elemzésével is behatóan foglalkozott. 1961 januárjában
Jánossy Lajos levelet kapott Princetonból egyik
barátjától, aki felhívta figyelmét Dicke tervezett kísérletére,
és arra kérte, hogy próbáljon kapcsolatot teremteni
Dicke és Renner között, hogy a majdnem 30
éves Renner-kísérletek néhány homályos pontját tisztázhassák.
Mint később kiderült, elsősorban e kísérletek
pontossága és a kiértékelés módja terén voltak
kételyeik.
Renner biztosította őket, hogy a zavaró hatások
kiküszöbölése és a kiértékelés terén is lényegében
ugyanúgy járt el, mint Eötvös, de jobb ingája volt és
hosszabb mérési sorozatai. Elküldte nekik egyik méréssorozatának
teljes adatsorát és kiértékelését, amit
Dicke munkatársai lelkiismeretesen átszámoltak (e
leveleket és a számolásokat később Renner hagyatékában,
az MTA levéltárában találtam meg). Fő kritikájuk
arra irányult, hogy Renner (mint valószínűleg korábban
Eötvös is) a korábbi és későbbi mérésekből
interpolált inga-leolvasásokat is független mérésként
kezelte, ami az adatok hibáit korrelálttá tette. Emiatt
az átlag valódi mérési hibája az eredetileg számítottnál
nagyobb (a Dicke-csoport szerint 2-es, illetve 3-as
faktorral, saját későbbi számításaim szerint 2,4-es faktorral).
E megnövelt hibákhoz képest viszont a Renner
által különböző anyagpárokra megadott eltérések
túl kicsik. Ennek oka nem tisztázódott, ami később
oda vezetett, hogy Renner eredményeit nem fogadták
el teljes értékűnek.
Dicke és csoportja szimmetrikusabb torziós ingát
használt, és Nap irányú gyorsulás alapján ellenőrizte
az ekvivalenciaelvet; mintegy 10-11 relatív pontosságot
értek el [5]. Néhány évvel később Braginsky és Panov
Moszkvában hagyományosabb, de igen hosszú lengésidejű
ingákkal állításuk szerint 10-12 pontosságot
ért el [6], szintén Nap irányú gyorsulást felhasználva.
Az ekvivalenciaelv még erősebb formáját ellenőrizte
az a kísérletsorozat, amely az Apolló-program során
Holdra juttatott fényvisszaverő tükröket használt
fel. A távolságok pontos mérésével ellenőrizhető,
hogy a Föld és Hold ugyanolyan gyorsulással "esik"-e
a Nap felé, noha tömegükben a gravitációs kötési
energia hányada nagyon különböző. A ma már 10-13
relatív pontosságú mérések szerint a két test ugyanúgy
esik, és a kötési energiára is nagy pontossággal
érvényes a súlyos és tehetetlen tömeg arányossága. E
pontos mérések alapján úgy tűnt, hogy az EPF- és
Renner-mérések eredményei túlhaladottakká váltak,
és már csak történeti jelentőségük van. Egy új hipotézis azonban
rácáfolt erre a feltételezésre.
Az "ötödik erő" hipotézise és
az EPF-kísérletek reneszánsza
1986-ban jelent meg Ephraim Fischbach és munkatársai
cikke az "ötödik erő" hipotéziséről [7]. Nagy
meglepetést keltett, hogy az új, anyagösszetételtől is
függő, Yukawa-típusú távolságfüggést mutató kölcsönhatás
hipotézise elsősorban a régi EPF-kísérletek
eredményeire támaszkodott (bizonyos geofizikai
módszerekkel kapott G-mérések és semleges kaonokkal
kapcsolatos gyorsítós mérések mellett). A
cikk nem kevesebbet állít, mint hogy az EPF-mérések
eredménye csak azért tűnt negatívnak, mert Eötvös
idejében még nem volt meg az a rendszerező elv,
amelynek alapján a különböző anyagpárokra vonatkozó
kis, önmagukban nem szignifikáns különbségeket
megfelelő sorrendbe lehetett volna állítani. A feltevés
szerint az új erő forrása nem maga a tömeg,
hanem a barionok (protonok és neutronok) száma,
az erő hatótávolsága pedig mindössze néhány száz
méter. Az atommagok kötési energiája (tömeghiánya)
miatt az erősen kötött magokban (pl. vasban)
egységnyi tömegre több barion jut, mint a gyengén
kötött magokban. A szerzők a Renner-kísérlet eredményeivel
nem foglalkoztak, mert azokat Dicke kritikája
némileg diszkreditálta. A Nap irányú gyorsulást
felhasználó, még pontosabb mérések viszont azért
nem cáfolták az ötödik erő létét, mert annak feltételezett
hatótávolsága a Nap távolságánál sokkal rövidebb.
A feltételezett új erő egyrészt sérti az ekvivalenciaelvet,
másrészt módosítja a gravitációs erőnél megszokott
1/r 2-tel arányos távolságfüggést. Az új erőt Fischbachék
két paraméterrel jellemezték: a 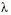 hatótávolsággal
és a kölcsönhatás gravitációhoz viszonyított,
kis távolságra érvényes
hatótávolsággal
és a kölcsönhatás gravitációhoz viszonyított,
kis távolságra érvényes 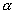 erősségével, ahol
erősségével, ahol
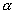 függ a
két test barionszám/tömeg arányától is. A gravitáció
és az ötödik erő együttes potenciálját a következő
kifejezéssel írták le:
függ a
két test barionszám/tömeg arányától is. A gravitáció
és az ötödik erő együttes potenciálját a következő
kifejezéssel írták le:
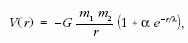
ahol G a gravitációsállandó nagy távolságokra érvényes
értéke, m1 és m2 a két tömeg, r
pedig azok távolsága.
A laboratóriumi G-mérések eszerint valójában
nem G, hanem G(1+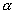 )
értékét mérik, ezért tér el egymástól
a laboratóriumi és geofizikai mérések eredménye.
Az
)
értékét mérik, ezért tér el egymástól
a laboratóriumi és geofizikai mérések eredménye.
Az 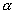 paraméter értékét -0,007-re,
paraméter értékét -0,007-re,
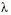 értékét pedig
200 m körülire becsülték.
Fischbachék cikkét követően mind az összetételfüggés,
mind a távolságfüggés ellenőrzésére talán
száznál is több, igen változatos módszerekkel végzett
kísérleti vizsgálat indult, amelyek a 90-es években -
több közbülső, pozitívnak látszó eredmény után -
végül negatív eredménnyel zárultak. E kísérletek
azonban hatékonyan fejlesztették a kísérleti technikát,
az elméleti meggondolások pedig sok érvvel támasztották
alá azt a várakozást, hogy mind az ekvivalenciaelv,
mind az 1/r2-es távolságfüggés valamilyen
szinten azért sérülhet.
értékét pedig
200 m körülire becsülték.
Fischbachék cikkét követően mind az összetételfüggés,
mind a távolságfüggés ellenőrzésére talán
száznál is több, igen változatos módszerekkel végzett
kísérleti vizsgálat indult, amelyek a 90-es években -
több közbülső, pozitívnak látszó eredmény után -
végül negatív eredménnyel zárultak. E kísérletek
azonban hatékonyan fejlesztették a kísérleti technikát,
az elméleti meggondolások pedig sok érvvel támasztották
alá azt a várakozást, hogy mind az ekvivalenciaelv,
mind az 1/r2-es távolságfüggés valamilyen
szinten azért sérülhet.
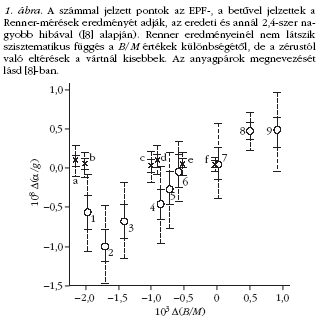
Bár az eredeti Fischbach-hipotézis ma már halott,
érdemes felidézni a nehézségi gyorsulások EPF- és
Renner-kísérletekben talált kis relatív különbségeit a
B/M (barionszám/tömeg) különbségek függvényében,
saját egykori számításaim alapján. Míg az EPF-kísérletek
eredményei valóban pozitív korrelációt
sejtetnek, Rennernél ennek nyomát sem találjuk
(1. ábra). Az eredeti hibaszámítást korrigáló megnövelt
szórás miatt az EPF-korreláció sem látszik szignifikánsnak.
A Renner-méréseknél viszont továbbra is
talányos, miért ilyen kicsik a zérustól való eltérések.
Valószínűleg érdemes lenne az általa alkalmazott
hibaszámítást még részletesebben, a lassú külső eredetű
változások statisztikáját is figyelembe véve újra megvizsgálni.
Eötvös-típusú kísérletek szerepe a modern
kozmológia és a nagy egyesítések korában
Az "ötödik erő" hipotézise Eötvös Loránd nevét és az
EPF-kísérleteket világszerte ismertté tette, ezért azóta a
kísérletek tágabb körét tekintik "Eötvös-típusúnak",
mint korábban. Röviddel a Fischbach-sejtés közlése
után alakult a Washingtoni Egyetemen (Seattle-ben)
Eric Adelberger vezetésével egy csoport, amely azóta is
főként kisméretű, precíziós torziós ingák segítségével
végzi a fizika és kozmológia alapjait érintő kísérleteit.
Ez a csoport Eötvös tiszteletére az "Eöt-Wash" nevet
vette fel, és azóta is ezen a néven működik [9]. Ma is ők
tartják a súlyos és tehetetlen tömeg arányára vonatkozó
pontossági rekordot (10-13). A Nap és Föld irányú gyorsulás
mellett vizsgálták a Galaxis központja felé irányuló
gyorsulásban esetleg meglévő anyagfüggést is, ami
azért érdekes, mert így az Univerzum tömegének jelentős
részét kitevő "sötét anyag" vonzására is kiterjeszthető
a kétféle tömeg arányossága. Felmerült annak elméleti
lehetősége is, hogy a tömeg mellett a spin is szerepet
kaphat a gravitációs kölcsönhatásban. Ennek ellenőrzésére
spin-polarizált anyagok felhasználásával is
végeztek igen érzékeny ingaméréseket. A Hold lézeres
megfigyelései során felmerült az a probléma, hogy az
ekvivalenciaelvtől való eltérések egyrészt a Hold és
Föld gravitációskötési energiahányadának különbözősége,
másrészt a két test eltérő összetétele miatt is felléphetnének.
Szerencsétlen esetben a két hatás kompenzálhatja
egymást. Az Eöt-Wash csoport ezért olyan
torziós ingát szerkesztett, amely a Földdel, illetve Holddal
azonos összetételű kis próbatesteket hasonlított
össze, és itt sem talált különbséget. Ez szigorúan is bizonyította
a gravitációskötési energiára fennálló ekvivalenciaelvet.
Az ekvivalenciaelv Földön megvalósítható vizsgálatainál
sokkal pontosabb érhető el űrbeli kísérletekben.
Már mintegy 20 éve tervezés alatt áll a STEP (Satellite
Test of the Equivalence Principle) kísérlet, ami a jelenleginél
5 nagyságrenddel nagyobb relatív pontosságot
(10-18) érhetne el. Egy Pisában 1993-ban rendezett
STEP-konferencián Eötvös érdemeinek felsorolásával
amellett próbáltam érvelni [10], hogy a kísérlet neve inkább
Eötvös legyen (esetleg "Equivalence Orbital Test
for a Variety Of Substances" rövidítéseként). Várható,
hogy az elkövetkező években az ekvivalenciaelvet
vizsgáló több űrkísérlet is előkészítési szakaszba lép, s
valamelyiküknél talán Eötvös neve is megjelenik.

Felvethető, hogy mi értelme van az ekvivalenciaelv
eddigieknél is pontosabb vizsgálatának. Korunk két
alapvető elmélete az elemi részecskék világát leíró,
modern kvantumelméleten alapuló térelmélet és a
gravitációt leíró általános relativitás elmélet. Mindeddig
egyiknek a jóslatait sem sikerült mérésekkel megcáfolni,
igen sok próbát kiálltak. Ugyanakkor a két
elmélet nem látszik összeegyeztethetőnek. Valamilyen
szinten eltérést kell találni a két elméletből
külön-külön következő jóslatoktól, hogy a kettő közötti
kapcsolatok megértéséhez kulcsot találjunk. E
várakozás ösztönzi nemcsak az ekvivalenciaelv egyre
szigorúbb ellenőrzését, de a hatalmas gyorsítók és
távcsövek építését is.
Az ekvivalenciaelv esetleges sérülése mellett napjaink
másik fontos elméleti várakozása, hogy a gravitáció
1/r2-es távolságfüggése nem igaz minden korlát
nélkül. Nagy méretekben a mindeddig hiába keresett
részecskékhez kapcsolható sötét anyag és az Univerzum
egyre gyorsuló tágulását előidéző sötét energia
okoz problémát, és sokan a gravitáció távolságfüggésének
módosulását sejtik ilyen nagy távolságokon.
Igen kis távolságokon szintén módosulhat a gravitációs
erőtörvény, hiszen a távolság csökkenésével egyre
erősebben jelentkezhetnek különböző kvantumeffektusok.
Olyan jóslatok is vannak, hogy mintegy
tized mm alatt a gravitáció a szokásos három térbeli
dimenzió mellett további dimenziókba is be tud hatolni,
és emiatt ennél kisebb távolságokon az 1/r2-es
távolságfüggés például 1/r4-re módosul. Más típusú
módosulást jósol a "kövér graviton" elmélet, amely
szerint kisméretekben a gravitációserő nem erősödik,
hanem gyengül a távolság csökkenésével. Ez magyarázhatná
a "sötét energia" nemrégiben kimért
energiasűrűségének kicsiny voltát is, hiszen ekkor a
nagyon kis hullámhosszú zéruspontrezgések nem járulnának
hozzá az Univerzum energiájához. E kérdések
vizsgálatához is alkalmasnak látszanak az
Eöt-Wash csoport torziós ingái.
Nemrégiben jelent meg az Eöt-Wash csoport új cikke
[11], amelyben egy torziós szálon függő, sok szabályosan
elhelyezett lyukat tartalmazó korong és egy
alatta elhelyezett, két rétegben szintén igen sok lyukat
tartalmazó forgótárcsa segítségével vizsgálták a gravitáció
távolságfüggését. A lyukak elrendezése olyan
volt, hogy a korong és tárcsa közti megfelelő távolság
és 1/r2-es távolságfüggés esetén gyakorlatilag ne gyakoroljanak
egymásra forgatónyomatékot (2. ábra).
Az igen gondos, hosszan tartó mérés során kimutatták,
hogy az 1/r2-es távolságfüggés mintegy 50 mikrométer
távolság fölött már igaz, ami kizár több korábbi
jóslatot, így a sötét energia "kövér gravitonokkal" való
egyszerű magyarázatát is. Persze mindig léteznek
bonyolultabb magyarázatok, és Adelberger csoportja
valószínűleg még tovább fogja finomítani mérési
módszereit.
Érdekes elgondolni, mit szólna Eötvös Loránd, ha
tudná, hogy ingája nyomán, amely "egyszerű volt,
mint Hamlet fuvolája", ma olyan érzékeny mérőműszerek
születnek, amelyek az Univerzum fő összetevőjének
mibenlétét is képesek minden más műszernél
pontosabban vizsgálni.
Végül felhívom az olvasók figyelmét, hogy Eötvös
Loránd életéről, tevékenységéről és munkáiról a világhálón
is sok információt találhatnak. Az Eötvös Loránd
Geofizikai Intézet tartja fenn a virtuális Eötvös-múzeum
honlapját [12], míg a KFKI tudománytörténeti
honlapján [13] sok más, Eötvössel kapcsolatos
anyag mellett az e cikk alapjául szolgáló előadás képei
is megtalálhatók [14].
Irodalom
- . R. v. Eötvös, D. Pekár, E. Fekete, Annalen der Physik 68 (1922) 11
- . Roland Eötvös gesammelte Arbeiten. Összeállította: Selényi Pál,
Akadémiai Kiadó, Budapest (1953)
- . Renner J., Kísérleti vizsgálatok a tömegvonzás és tehetetlenség
arányosságáról. Matematikai és Természettudományi Értesíto
13 (1935) 542
- . J. Illy, Einstein und der Eötvös-Versuch: ein Brief Albert Einsteins
an Willy Wien. Annals of Science 46 (1989) 417
- . P.G. Roll, R. Krotkov, R.H. Dicke, The equivalence of inertial
and passive gravitational mass. Ann. Phys. (NY) 26 (1964) 442
- . V.B. Braginsky, V.I. Panov, Verification of Equivalence Principle
of Inertial and Gravitational Mass. Zh. Eksp. Teor. Fiz. 61 (1971)
873, vagy Sov. Phys. JETP 34 (1972) 463
- . E. Fischbach et al., Reanalysis of the Eötvös Experiment. Phys.
Rev. Lett. 56 (1986) 3
- . Fischbach, E., Bod L., Nárayné Ziegler M., Marx Gy., Az Eötvös-kísérlet
száz éve. www.kfki.hu/eotvos/szazeves.html
- . Az Eöt-Wash csoport honlapja:
www.npl.washington.edu/eotwash/
- . Király P., Eötvös and STEP.
http://www.kfki.hu/~tudtor/eotvos1/stepcikk.html
- . D.J. Kapner et al., Tests of the gravitational inverse-square law
below the dark-energy length scale. arXiv:hep-ph/0611184
(2006) - Phys. Rev. Lett. 98 (2007) 021101
- . Eötvös Loránd virtuális múzeum: www.elgi.hu/museum/
- . Eötvös Loránd munkái és méltatása: www.kfki.hu/eotvos/
- . Király P., Ünnepi előadás 2006. nov. 22-én.
www.kfki.hu/eotvos/eotvoseloadas06.pdf
_____________________________________________________
A cikk az MTA XI. Osztálya és az ELFT közös ünnepi ülésén 2006.
november 22-én elhangzott előadásalapján készült.
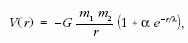
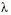 hatótávolsággal
és a kölcsönhatás gravitációhoz viszonyított,
kis távolságra érvényes
hatótávolsággal
és a kölcsönhatás gravitációhoz viszonyított,
kis távolságra érvényes 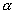 erősségével, ahol
erősségével, ahol
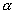 függ a
két test barionszám/tömeg arányától is. A gravitáció
és az ötödik erő együttes potenciálját a következő
kifejezéssel írták le:
függ a
két test barionszám/tömeg arányától is. A gravitáció
és az ötödik erő együttes potenciálját a következő
kifejezéssel írták le:
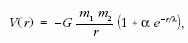
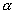 )
értékét mérik, ezért tér el egymástól
a laboratóriumi és geofizikai mérések eredménye.
Az
)
értékét mérik, ezért tér el egymástól
a laboratóriumi és geofizikai mérések eredménye.
Az 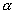 paraméter értékét -0,007-re,
paraméter értékét -0,007-re,
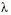 értékét pedig
200 m körülire becsülték.
Fischbachék cikkét követően mind az összetételfüggés,
mind a távolságfüggés ellenőrzésére talán
száznál is több, igen változatos módszerekkel végzett
kísérleti vizsgálat indult, amelyek a 90-es években -
több közbülső, pozitívnak látszó eredmény után -
végül negatív eredménnyel zárultak. E kísérletek
azonban hatékonyan fejlesztették a kísérleti technikát,
az elméleti meggondolások pedig sok érvvel támasztották
alá azt a várakozást, hogy mind az ekvivalenciaelv,
mind az 1/r2-es távolságfüggés valamilyen
szinten azért sérülhet.
Bár az eredeti Fischbach-hipotézis ma már halott,
érdemes felidézni a nehézségi gyorsulások EPF- és
Renner-kísérletekben talált kis relatív különbségeit a
B/M (barionszám/tömeg) különbségek függvényében,
saját egykori számításaim alapján. Míg az EPF-kísérletek
eredményei valóban pozitív korrelációt
sejtetnek, Rennernél ennek nyomát sem találjuk
(1. ábra). Az eredeti hibaszámítást korrigáló megnövelt
szórás miatt az EPF-korreláció sem látszik szignifikánsnak.
A Renner-méréseknél viszont továbbra is
talányos, miért ilyen kicsik a zérustól való eltérések.
Valószínűleg érdemes lenne az általa alkalmazott
hibaszámítást még részletesebben, a lassú külső eredetű
változások statisztikáját is figyelembe véve újra megvizsgálni.
értékét pedig
200 m körülire becsülték.
Fischbachék cikkét követően mind az összetételfüggés,
mind a távolságfüggés ellenőrzésére talán
száznál is több, igen változatos módszerekkel végzett
kísérleti vizsgálat indult, amelyek a 90-es években -
több közbülső, pozitívnak látszó eredmény után -
végül negatív eredménnyel zárultak. E kísérletek
azonban hatékonyan fejlesztették a kísérleti technikát,
az elméleti meggondolások pedig sok érvvel támasztották
alá azt a várakozást, hogy mind az ekvivalenciaelv,
mind az 1/r2-es távolságfüggés valamilyen
szinten azért sérülhet.
Bár az eredeti Fischbach-hipotézis ma már halott,
érdemes felidézni a nehézségi gyorsulások EPF- és
Renner-kísérletekben talált kis relatív különbségeit a
B/M (barionszám/tömeg) különbségek függvényében,
saját egykori számításaim alapján. Míg az EPF-kísérletek
eredményei valóban pozitív korrelációt
sejtetnek, Rennernél ennek nyomát sem találjuk
(1. ábra). Az eredeti hibaszámítást korrigáló megnövelt
szórás miatt az EPF-korreláció sem látszik szignifikánsnak.
A Renner-méréseknél viszont továbbra is
talányos, miért ilyen kicsik a zérustól való eltérések.
Valószínűleg érdemes lenne az általa alkalmazott
hibaszámítást még részletesebben, a lassú külső eredetű
változások statisztikáját is figyelembe véve újra megvizsgálni.