Fizikai Szemle 2007/2. 47.o.
SZIMMETRIÁK ÉS SÉRTÉSÜK A RÉSZECSKÉK VILÁGÁBAN
- A PARITÁSSÉRTÉS 50 ÉVE
Horváth Dezső
MTA KFKI RMKI,
Budapest és ATOMKI, Debrecen
Az Eötvös Loránd Fizikai Társulat 2006. május 27-i közgyűlésén
elhangzott előadás alapján.
Tükrözési szimmetria és paritás
Ahogyan egy korábbi cikkemben [1] leírtam, a részecskefizikában
a szimmetriák mindenütt jelen vannak:
a kölcsönhatások tulajdonságaiban, a megmaradási
törvények hátterében, az összetett részecskék
szerkezetében. A szimmetriasértések szerepe ugyanilyen
jelentős: a részecskefizika Standard Modellje
szerint a részecskék az elektrogyenge kölcsönhatás
szimmetriájának "spontán sérülése" következtében
nyernek tömeget, és ennek a "spontán sérülési" mechanizmusnak
a mellékterméke a részecskefizika
talán legmisztikusabb objektuma, a Higgs-bozon.1 Ezt
a hipotetikus részecskét még egyetlen kísérletben
sem sikerült "láthatóvá" tenni, de létezése elengedhetetlenül
fontos az elmélet szempontjából: lehetővé
teszi a mérhető folyamatok valószínűségeinek közelítő,
perturbatív, számítását (hacsak nem bizonyul túlságosan
"nehéznek").
A részecskefizika három alapvető tükrözési szimmetriája,
a töltés, a tér és az idő tükrözésével kapcsolatos.
A P tértükrözés ellenkezőjére fordítja a térkoordináták
előjelét, ami annak felel meg, mintha a rendszert
a szokásos jobbkezes koordinátarendszer helyett
balkezesben írnánk le. A T időtükrözés az időkoordinátát
fordítja ellenkezőjére. A C töltéstükrözés részecskéből
antirészecskét csinál: valamennyi töltés
típusú kvantumszám előjelét megfordítja.
Egy függvény páros, ha változójának előjelét megfordítva,
tükrözve, értéke nem változik, páratlan, ha
azonos abszolút érték mellett előjelet vált. Páros
függvény, például, f (x) = A cosx és páratlan f (x) =
A sinx.
A részecskék állapotfüggvényeinek tanulmányozásánál
kiderült, hogy a párosság vagy paritás jellemző
tulajdonságuk, amely az ütközési és bomlási reakciók
során általában megőrződik. Az l mellékkvantumszámra
gerjesztett hidrogénállapot hullámfüggvénye,
például, a tértükrözés hatására változatlan abszolút
érték mellett egy (-1)l szorzót kap, azaz a paritása
(-1)l. Mivel a legegyszerűbb E1 fotonátmenet
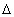 l = 1
változást jelent, a fotonhoz a paritás megmaradását
feltételezve a P
l = 1
változást jelent, a fotonhoz a paritás megmaradását
feltételezve a P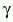 = -1 negatív paritás rendelhető. A
többi részecskének is van saját paritása, a fermionok
jellegzetessége, hogy részecske és antirészecske paritása
ellentétes előjelű. Sok-sok megfigyelésből leszűrve
a tapasztalatot a paritást megmaradó fizikai mennyiségként
fogadták el.
Mivel összetett rendszerekben az alkotórészek paritásai
összeszorzódnak, a kvark + anti-kvark kötött
állapotként leírható mezonok alapállapotban (amikor
a kvarkok egymáshoz képesti mozgásának impulzusmomentuma
zérus) negatív paritással rendelkeznek;
az esetleges L relatív impulzusmomentum, a hidrogénatomhoz
hasonlóan, a kötött állapot saját-impulzusmomentumához
(-1)L szorzóval járul.
A fizika jelenlegi állása szerint a három tükrözés
együttes alkalmazása nem változtatja meg egy fizikai
rendszer mérhető tulajdonságait, azaz egy szabad
antirészecske matematikailag úgy kezelhető, mint egy
térben és időben visszafelé mozgó részecske. Az
elektron és antirészecskéje, a pozitron kétfotonos
annihilációját úgy írjuk le, mintha egy elektron megjelenne,
kibocsátana két fotont, majd térben és időben
kihátrálna a képből. A CPT-invariancia a térelmélet
egyik alaptétele, sértéséhez olyan alapvető fizikai
feltevésekről kellene lemondanunk, mint a Lorentz-invariancia
vagy a kauzalitás.
= -1 negatív paritás rendelhető. A
többi részecskének is van saját paritása, a fermionok
jellegzetessége, hogy részecske és antirészecske paritása
ellentétes előjelű. Sok-sok megfigyelésből leszűrve
a tapasztalatot a paritást megmaradó fizikai mennyiségként
fogadták el.
Mivel összetett rendszerekben az alkotórészek paritásai
összeszorzódnak, a kvark + anti-kvark kötött
állapotként leírható mezonok alapállapotban (amikor
a kvarkok egymáshoz képesti mozgásának impulzusmomentuma
zérus) negatív paritással rendelkeznek;
az esetleges L relatív impulzusmomentum, a hidrogénatomhoz
hasonlóan, a kötött állapot saját-impulzusmomentumához
(-1)L szorzóval járul.
A fizika jelenlegi állása szerint a három tükrözés
együttes alkalmazása nem változtatja meg egy fizikai
rendszer mérhető tulajdonságait, azaz egy szabad
antirészecske matematikailag úgy kezelhető, mint egy
térben és időben visszafelé mozgó részecske. Az
elektron és antirészecskéje, a pozitron kétfotonos
annihilációját úgy írjuk le, mintha egy elektron megjelenne,
kibocsátana két fotont, majd térben és időben
kihátrálna a képből. A CPT-invariancia a térelmélet
egyik alaptétele, sértéséhez olyan alapvető fizikai
feltevésekről kellene lemondanunk, mint a Lorentz-invariancia
vagy a kauzalitás.

A paritássértés felfedezése
A paritássértés felfedezése a 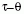 paradoxonnak köszönhető.
Megfigyeltek két részecskét, amelyek valamennyi
tulajdonsága azonos volt a paritásuk kivételével,
a
paradoxonnak köszönhető.
Megfigyeltek két részecskét, amelyek valamennyi
tulajdonsága azonos volt a paritásuk kivételével,
a 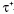 -mezon ugyanis gyenge kölcsönhatásban két
-mezon ugyanis gyenge kölcsönhatásban két
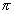 -mezonra (pionra), amíg a
-mezonra (pionra), amíg a 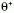 három pionra bomlott.
Figyelembe véve a pion negatív paritását, ez a
három pionra bomlott.
Figyelembe véve a pion negatív paritását, ez a 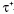 -nak
pozitív, a
-nak
pozitív, a 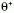 -nak negatív paritást adott.
Tsung-Dao Lee és Chen-Ning Yang (1. ábra) a
fenti kérdés megoldását keresve 50 évvel ezelőtt megvizsgálta
[2] a paritásmegmaradás kísérleti bizonyítékait
és megállapította, hogy valamennyi elektromágneses
jelenségeken alapul. Feltételezték, hogy a
-nak negatív paritást adott.
Tsung-Dao Lee és Chen-Ning Yang (1. ábra) a
fenti kérdés megoldását keresve 50 évvel ezelőtt megvizsgálta
[2] a paritásmegmaradás kísérleti bizonyítékait
és megállapította, hogy valamennyi elektromágneses
jelenségeken alapul. Feltételezték, hogy a 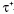 és
a
és
a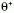 ugyanaz a részecske (azt ma K+ mezonnak hívjuk),
viszont a gyenge kölcsönhatás sérti a paritásmegmaradást,
és javasoltak néhány kísérletet a paritássértés
ellenőrzésére. A kísérleti ellenőrzés azonnal
megkezdődött, és igazolta a paritássértést; Lee és
Yang még 1957-ben megkapta a Nobel-díjat. (Elfilozofálhatunk
azon, hány cikk kell a Nobel-díjhoz: általában
egy, ha az elég jó.)
ugyanaz a részecske (azt ma K+ mezonnak hívjuk),
viszont a gyenge kölcsönhatás sérti a paritásmegmaradást,
és javasoltak néhány kísérletet a paritássértés
ellenőrzésére. A kísérleti ellenőrzés azonnal
megkezdődött, és igazolta a paritássértést; Lee és
Yang még 1957-ben megkapta a Nobel-díjat. (Elfilozofálhatunk
azon, hány cikk kell a Nobel-díjhoz: általában
egy, ha az elég jó.)
Az első kísérlet Chien-Shiung Wu asszony (1. ábra)
nevéhez fűződik [3]. 60Co izotópot mágneses térbe
helyezve lehűtöttek csaknem az abszolút zérus hőmérsékletre
(0,1 K alá). A 60Co mag instabil, béta-bomlással
a 60Ni izotóp gerjesztett állapotává alakul, azaz egyik
neutronja protonra, elektronra és antineutrínóra bomlik:
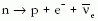 .
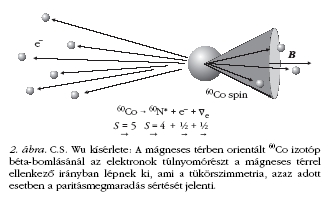
Mivel a 60Co S = 5, a 60Ni S = 4, a
kirepülő elektron és antineutrínó pedig S = 1/2 spinnel
rendelkezik, a megmaradási törvények előírják, hogy a
végállapoti részecskék impulzusmomentuma a 60Co-é
irányába mutasson (2. ábra). A mágneses tér a 60Co impulzusmomentumát
beállítja, a hűtés pedig a rezgését
minimalizálja, a kirepülő elektron impulzusmomentuma
(spinje) tehát a mágneses tér irányába fog mutatni.
A neutrínó spinje, elhanyagolhatóan kicsi tömege miatt,
párhuzamos az impulzusával. A paritásmegmaradás itt
tükörszimmetriát feltételez, akkor tehát az elektronok
valamennyi irányban egyforma valószínűséggel repülnek,
annak sértése viszont valamelyik irányt előnyben
fogja részesíteni.
.
Mivel a 60Co S = 5, a 60Ni S = 4, a
kirepülő elektron és antineutrínó pedig S = 1/2 spinnel
rendelkezik, a megmaradási törvények előírják, hogy a
végállapoti részecskék impulzusmomentuma a 60Co-é
irányába mutasson (2. ábra). A mágneses tér a 60Co impulzusmomentumát
beállítja, a hűtés pedig a rezgését
minimalizálja, a kirepülő elektron impulzusmomentuma
(spinje) tehát a mágneses tér irányába fog mutatni.
A neutrínó spinje, elhanyagolhatóan kicsi tömege miatt,
párhuzamos az impulzusával. A paritásmegmaradás itt
tükörszimmetriát feltételez, akkor tehát az elektronok
valamennyi irányban egyforma valószínűséggel repülnek,
annak sértése viszont valamelyik irányt előnyben
fogja részesíteni.
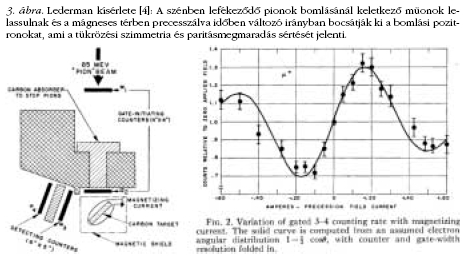
Az eredmény megdöbbentette a fizikusvilágot: az
elektronok túlnyomórészt a mágneses térrel ellenkező
irányban léptek ki (2. ábra), ami azt jelentette, hogy a
gyenge kölcsönhatás maximálisan sérti a tükörszimmetriát
és a paritás megmaradását:
a mozgásiránnyal szemben
(balra) polarizált részecskéket
és a mozgásirányban
(jobbra) polarizált antirészecskéket
részesíti előnyben. Wolfgang
Pauli az eredmény hallatán
kijelentette: Nem tudom
elhinni, hogy Isten balkezes!
Az ugyancsak a Columbia egyetemen
dolgozó Leon Lederman
csoportja, hallván a
Wu-kísérlet első eredményeiről,
sokkal egyszerűbb mérésbe
kezdett [4]. Pozitív pionokat
állítottak meg szénben. A
pionok gyenge kölcsönhatásban
elbomlanak müonok kibocsátásával,
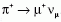 . A müonok polarizáltan keletkeznek:
mivel a pion spinje zérus és a keletkező leptonoké
1/2, az impulzusmegmaradás miatt a müon és a
neutrínó spinje egymással szemben fog állni. A müon
bomlása is gyenge kölcsönhatás,
. A müonok polarizáltan keletkeznek:
mivel a pion spinje zérus és a keletkező leptonoké
1/2, az impulzusmegmaradás miatt a müon és a
neutrínó spinje egymással szemben fog állni. A müon
bomlása is gyenge kölcsönhatás, 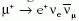 és ha
nincs tükörszimmetria, a pozitronok a müon polarizációs
irányában fognak kilépni. A müonok mágneses
térben precesszálnak, azaz a spinjük kis mágnesként
forog, a pozitronokat tehát a tükörszimmetria sértése
esetén a rögzített helyzetű detektor időben változó
intenzitással észleli. Amint a 3. ábra mutatja, a kilépő
pozitronok valóban a müon spinjének irányát követik,
a paritás tehát nem marad meg ebben az esetben sem.
és ha
nincs tükörszimmetria, a pozitronok a müon polarizációs
irányában fognak kilépni. A müonok mágneses
térben precesszálnak, azaz a spinjük kis mágnesként
forog, a pozitronokat tehát a tükörszimmetria sértése
esetén a rögzített helyzetű detektor időben változó
intenzitással észleli. Amint a 3. ábra mutatja, a kilépő
pozitronok valóban a müon spinjének irányát követik,
a paritás tehát nem marad meg ebben az esetben sem.
A Lederman-kísérlet néhány nap alatt igazolta a
paritássértés elméletét, a szerzők azonban nem közölték
eredményüket addig, amíg a Wu-csoport is el nem
készült. Így a két cikk, [3] és [4] a
Physical Review
ugyanazon számában, egymást követve jelent meg;
Wuék Lee-nek és Yangnak mondtak köszönetet az
elméletért, míg Ledermanék Lee-nek az elmélet elmagyarázásáért
és Wunak előzetes eredménye közléséért.
Nem sokkal később Telegdi Bálint kísérlete is
igazolta a gyenge kölcsönhatás paritássértését.
A Lederman-kísérlet messzemenően túlmutatott a
paritássértés igazolásán: nemcsak sikerült megmérniük
a müon mágneses momentumát, de alapjául
szolgált a ma már széles körben elterjedt szilárdtestfizikai-
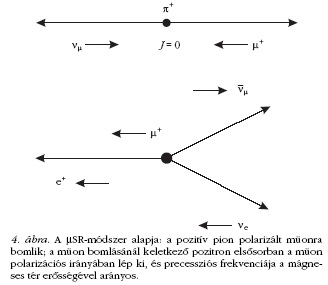
kémiai vizsgálati módszernek, a µSR-nek. A rövidítés
jelentése hármas: müonspin-rezonancia, -rotáció
és -relaxáció. A módszer elve az, hogy a polarizált
müonok precessziós frekvenciája,
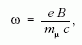
a müon helyén méri a B mágneses teret (rotáció). Ez
jellegzetes értékeket vehet fel bizonyos kitüntetett
pontokban, például rácshibákban vagy kémiai gyökökkel
kötésben (rezonancia). A müon depolarizációs
ideje (relaxáció) is jellemzi a közeg mágneses tulajdonságait.
A CP-sértés felfedezése
Mint korábban említettem, a paritássértés felfedezése
megrázta a fizikusközösséget, és arra indította, hogy
olyan, addig abszolútnak tekintett szimmetriát is ellenőrizzen,
mint a töltés és a tér együttes tükrözésével
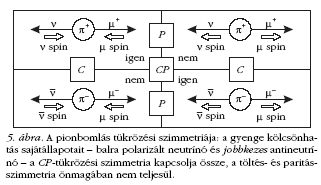
szembeni viselkedést kifejező CP-invariancia. A CP-tükrözés
hatását az 5. ábra illusztrálja: a pozitív és
negatív pion lehetséges bomlásai közül a gyenge kölcsönhatás
paritássértő volta csak azokat engedi meg,
amelyekben balra polarizált neutrínó és
jobbra polarizált antineutrínó keletkezik;
ezeket az állapotokat a CP-szimmetria
kapcsolja össze. Vegyük észre, hogy a
müonok polarizációja ennek ellentmond:
az impulzusmomentum megmaradása
azt diktálja, hogy a két keletkező
fermion spinje ellenkező irányba mutasson,
de a (csaknem) zérus tömegű neutrínóé csak
a mozgás egyenesébe eshet.
A paritássértés maximális volta vezet
tiszta végállapotokra.
A 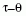 paradoxon tehát megoldódott,
a két részecske azonosnak bizonyult és
K-mezon (kaon) lett a neve. Négyféle
állapota van: K+, K-, K0 és anti-K0
(
paradoxon tehát megoldódott,
a két részecske azonosnak bizonyult és
K-mezon (kaon) lett a neve. Négyféle
állapota van: K+, K-, K0 és anti-K0
(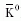 )
Az elektromosan semleges K0,
)
Az elektromosan semleges K0, 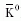 részecskék egyedülálló lehetőséget kínálnak
a CP-szimmetria megmaradásának ellenőrzésére.
Ha igaz a CP-szimmetria, akkor pozitív(negatív) CP-sajátállapot
pozitív(negatív) CP-sajátállapotba bomlik.
A K0 és
részecskék egyedülálló lehetőséget kínálnak
a CP-szimmetria megmaradásának ellenőrzésére.
Ha igaz a CP-szimmetria, akkor pozitív(negatív) CP-sajátállapot
pozitív(negatív) CP-sajátállapotba bomlik.
A K0 és 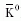 részecskék egyike sem CP-sajátállapot,
CPK0
részecskék egyike sem CP-sajátállapot,
CPK0 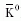 . (A CP-tükrözés itt egy a jelen cikk témá-
ján kívül eső, egyedül az erős kölcsönhatás által "tiszteletben
tartott" kvantumszám, a "ritkaság" előjelét
változtatja az ellenkezőjére.) CP-sajátállapotok a kettő
kombinációi lesznek:
. (A CP-tükrözés itt egy a jelen cikk témá-
ján kívül eső, egyedül az erős kölcsönhatás által "tiszteletben
tartott" kvantumszám, a "ritkaság" előjelét
változtatja az ellenkezőjére.) CP-sajátállapotok a kettő
kombinációi lesznek:
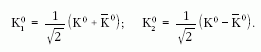
A CP-tükrözés hatására K2 előjelet vált, míg K1 nem,
tehát K1 CP-pozitív, K2 pedig CP-negatív állapot.
A K-mezonok gyenge bomlása pionokat eredményez.
Mivel a pion CP-negatív, a K1 kettő, a K2 három
pionra tud bomlani (egy piont az impulzusmegmaradás
tilt). A háromrészecskés bomlás valószínűsége
sokkal kisebb, ezért a K2 élettartama csaknem 3 nagyságrenddel
hosszabb, mint a K1-é. Ha tehát semleges
kaonokat keltünk, és elég sokáig várunk (például
hosszú nyalábvezetékben röptetve), a rövid élettartamú
K1 elbomlik, és csak a hosszú élettartamú K2
marad meg a részecskenyalábban. Christenson, Cronin,
Fitch és Turlay 1964-ben kimutatták [5], hogy az
így nyert tiszta K2 is tud - ha nagyon ritkán is - két
pionra bomlani, ami azt jelenti, hogy a gyenge kölcsönhatás
a CP-szimmetriát is sérti, nemcsak a P tükrözési
szimmetriát, bár a paritássértéssel ellentétben a
CP-sértés igen gyenge. Ennek az igen kicsi effektusnak
a kimutatásáért Cronin és Fitch is Nobel-díjat kapott,
igaz, csak 1980-ban.
A CPT-szimmetria ellenőrzése
Senki sem kételkedik komolyan a CPT-invariancia
érvényességében, hiszen az elméleti fizika egyik alaptételéről
van szó. Ugyanakkor a paritás- és a CP-sértés
felfedezése szinte kötelezővé teszi valamennyi
szimmetriatörvényünk lehető legpontosabb kísérleti
ellenőrzését. Kézenfekvő kísérlet részecske és antirészecske
tulajdonságainak összehasonlítása. A CPT-szimmetria
eddigi legpontosabb ellenőrzése a semleges
kaon és antikaon tömegének mérése: relatív különbségük
10-18-nál kisebbnek adódott. Igen pontosak
korunk lézerspektroszkópiai mérései (J.R. Hall és
T. Hänsch ezért kapott 2005-ben Nobel-díjat), így a
hidrogén és antihidrogén spektrumának összehasonlítása
is igen ígéretes (6. ábra).
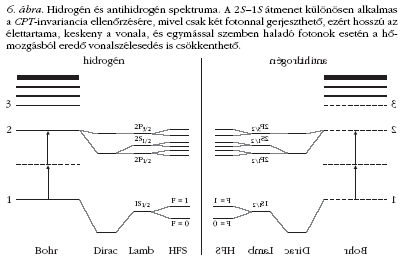
A CERN antiproton-lassító berendezése a CPT-invariancia
kísérleti ellenőrzésére épült, és jelenleg
három kutatócsoport is (ALPHA, ASACUSA és ATRAP)
antihidrogén-spektroszkópia előkészítésével foglalkozik.
A japán-osztrák-magyar ASACUSA emellett antiprotonokat
fogat be atomi pályákra, és lézerspektroszkópia
segítségével tanulmányozza az antiproton
átmeneteit. Ebből is igen precíz összehasonlításra
nyílik lehetőség az antiproton és a proton tömege és
töltése között.
Elveszett szimmetriák?
Amint láttuk, a CPT-szimmetria alapvető, abszolút és
a fizika jelenlegi állása szerint nem sérül. Láttuk, hogy
a gyenge kölcsönhatás az alapvető tükrözési szimmetriák
közül kettőt is sért, a paritásszimmetriát maximálisan,
a CP-invarianciát viszont csak parányit.
A részecskefizika mai elmélete, a Standard Modell
a kölcsönhatásokat bizonyos szimmetriák eleve feltételezéséből
származtatja (amelyeket aztán, mint említettük,
mégis sérteni kell). Kimagasló sikere ellenére,
hiszen az összes máig rendelkezésre álló részecskefizikai
mérési adatot kitűnően leírja, komoly nehézségekkel
küszködik. Nem tudja magába integrálni a
gravitációs kölcsönhatást, nem ad számot a Világegyetem
tömegének jelentős részét kitevő, rejtélyes
sötét anyagról, és nem magyarázza világunk furcsa
aszimmetriáit: miért nincsenek antianyag-galaxisok,
és a gyenge kölcsönhatás miért éppen a balra polarizált
részecskéket kedveli.

A fenti problémákat talán megoldja a szuperszimmetria
elmélete, amely feltételezi, hogy minden fermionnak
és minden bozonnak létezik azonos tulajdonságokkal
rendelkező párja a másik csoportban,
tehát például az elektronnak (S = 1/2) van egy hasonló
tömegű és töltésű S = 0 spinű partner részecskéje. Ez
a szimmetria alacsony energián biztosan sérül, hiszen
ezeket a részecskéket hiába kerestük az eddigi gyorsítós
kísérletekben, nem sikerült megfigyelnünk őket.
Ha léteznek, a tömegük a hidrogénatoménak legalább
százszorosa. Maga a modell viszont rendkívül vonzó,
mert pontos számításokat tesz lehetővé, nem mond
ellent az eddigi megfigyeléseknek és megoldja a Standard
Modell - legalábbis, bizonyos - problémáit. A
sötét anyag, például, magyarázható a legkönnyebb
szuperszimmetrikus részecske létezésével. A modell
szerint ugyanis nagyenergiájú részecskeütközésekben
keletkezhetnek szuperszimmetrikus részecske-antirészecske
párok, de azok, miután szétrepültek, a megmaradási
törvények miatt csak újabb szuperszimmetrikus
részecske kibocsátásával tudnak bomlani. Így a
legkönnyebb ilyen részecske stabil lesz, de elektromosan
semleges lévén, nem észlelhető, csak a gravitációs
hatásán keresztül.
Befejezésül idézem a Nobel-díjas Frank Wilczek
igen mély megfigyelését Elveszett szimmetriák nyomában
című cikkéből, amely a Nature a fizika évének
szentelt számában jelent meg [6]: "A fizika alapvető
egyenletei több szimmetriával rendelkeznek, mint az
aktuális fizikai világ." Valóban, láttunk több szimmetriát,
amely segít a matematikai formalizmus felépítésében,
de sérül: a térbeli tükrözését és a CP-szimmetriát
sérti a gyenge kölcsönhatás, a Higgs-mechanizmus
spontán szimmetriasértése segít a tömegképződésben
és az elektromos és gyenge kölcsönhatás
egyesítésében, az alacsony energián nyilvánvalóan
sérülő szuperszimmetria pedig segít a Standard Modell
elméleti nehézségeinek megoldásában.
<>
A szerző hálásan köszöni Tóth Kálmán segítő tanácsait a szimmetriák
tárgyalásával kapcsolatban. A témához kapcsolódó kutatásokat
az OTKA T042864 és T046095 és az EU FP6 509252 (RIPNP-GRID)
és 031688 (EGEE2) jelű pályázatai támogatják.
Irodalom
- . Horváth D., Szimmetriák az elemi részecskék világában,
Fizikai
Szemle 53/4 (2003) 122-127
- . T.-D. Lee, C.-N. Yang, Question of Parity Conservation in Weak
Interactions, Physical Review 104 (1956) 254-258
- . C.S. Wu és társai, Experimental Test of Parity Conservation in
Beta Decay, Physical Review 105 (1957) 1413-1414
- . R.L. Garwin, L.M. Lederman, M. Weinrich, Observations of the
Failure of Conservation of Parity and Charge Conjugation in Meson
Decays: the Magnetic Moment of the Free Muon, Physical
Review 105 (1957) 1415-1417
- . J.H. Christensen, J. Cronin, V. Fitch, R. Turlay, Evidence for the
2
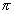 Decay of the
Decay of the
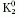 Meson, Physical Review Letters 13 (1964)
138-140
Meson, Physical Review Letters 13 (1964)
138-140
- . F. Wilczek, In search of symmetry lost, Nature 433 (2005) 239
________________________________________________________________
1 Elemi részecskéink
fermionok és bozonok, amelyeket J = S
saját-impulzumomentumuk (S spinjük) különbözteti meg: az összetett
részecskéket (mint például a proton, a neutron vagy a pion)
alkotó kvarkok, valamint a leptonok, (mint az elektron, a müon, a
neutrínók) S = 1/2 spinű fermionok. A bozonok spinje egész, ilyenek
a fermionok közötti kölcsönhatást közvetítő S = 1 spinű részecskék
(például a foton). A Higgs-bozon spinje zérus, S = 0.

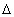 l = 1
változást jelent, a fotonhoz a paritás megmaradását
feltételezve a P
l = 1
változást jelent, a fotonhoz a paritás megmaradását
feltételezve a P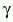 = -1 negatív paritás rendelhető. A
többi részecskének is van saját paritása, a fermionok
jellegzetessége, hogy részecske és antirészecske paritása
ellentétes előjelű. Sok-sok megfigyelésből leszűrve
a tapasztalatot a paritást megmaradó fizikai mennyiségként
fogadták el.
Mivel összetett rendszerekben az alkotórészek paritásai
összeszorzódnak, a kvark + anti-kvark kötött
állapotként leírható mezonok alapállapotban (amikor
a kvarkok egymáshoz képesti mozgásának impulzusmomentuma
zérus) negatív paritással rendelkeznek;
az esetleges L relatív impulzusmomentum, a hidrogénatomhoz
hasonlóan, a kötött állapot saját-impulzusmomentumához
(-1)L szorzóval járul.
A fizika jelenlegi állása szerint a három tükrözés
együttes alkalmazása nem változtatja meg egy fizikai
rendszer mérhető tulajdonságait, azaz egy szabad
antirészecske matematikailag úgy kezelhető, mint egy
térben és időben visszafelé mozgó részecske. Az
elektron és antirészecskéje, a pozitron kétfotonos
annihilációját úgy írjuk le, mintha egy elektron megjelenne,
kibocsátana két fotont, majd térben és időben
kihátrálna a képből. A CPT-invariancia a térelmélet
egyik alaptétele, sértéséhez olyan alapvető fizikai
feltevésekről kellene lemondanunk, mint a Lorentz-invariancia
vagy a kauzalitás.
= -1 negatív paritás rendelhető. A
többi részecskének is van saját paritása, a fermionok
jellegzetessége, hogy részecske és antirészecske paritása
ellentétes előjelű. Sok-sok megfigyelésből leszűrve
a tapasztalatot a paritást megmaradó fizikai mennyiségként
fogadták el.
Mivel összetett rendszerekben az alkotórészek paritásai
összeszorzódnak, a kvark + anti-kvark kötött
állapotként leírható mezonok alapállapotban (amikor
a kvarkok egymáshoz képesti mozgásának impulzusmomentuma
zérus) negatív paritással rendelkeznek;
az esetleges L relatív impulzusmomentum, a hidrogénatomhoz
hasonlóan, a kötött állapot saját-impulzusmomentumához
(-1)L szorzóval járul.
A fizika jelenlegi állása szerint a három tükrözés
együttes alkalmazása nem változtatja meg egy fizikai
rendszer mérhető tulajdonságait, azaz egy szabad
antirészecske matematikailag úgy kezelhető, mint egy
térben és időben visszafelé mozgó részecske. Az
elektron és antirészecskéje, a pozitron kétfotonos
annihilációját úgy írjuk le, mintha egy elektron megjelenne,
kibocsátana két fotont, majd térben és időben
kihátrálna a képből. A CPT-invariancia a térelmélet
egyik alaptétele, sértéséhez olyan alapvető fizikai
feltevésekről kellene lemondanunk, mint a Lorentz-invariancia
vagy a kauzalitás.
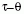 paradoxonnak köszönhető.
Megfigyeltek két részecskét, amelyek valamennyi
tulajdonsága azonos volt a paritásuk kivételével,
a
paradoxonnak köszönhető.
Megfigyeltek két részecskét, amelyek valamennyi
tulajdonsága azonos volt a paritásuk kivételével,
a 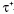 -mezon ugyanis gyenge kölcsönhatásban két
-mezon ugyanis gyenge kölcsönhatásban két
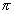 -mezonra (pionra), amíg a
-mezonra (pionra), amíg a 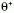 három pionra bomlott.
Figyelembe véve a pion negatív paritását, ez a
három pionra bomlott.
Figyelembe véve a pion negatív paritását, ez a 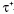 -nak
pozitív, a
-nak
pozitív, a 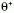 -nak negatív paritást adott.
Tsung-Dao Lee és Chen-Ning Yang (1. ábra) a
fenti kérdés megoldását keresve 50 évvel ezelőtt megvizsgálta
[2] a paritásmegmaradás kísérleti bizonyítékait
és megállapította, hogy valamennyi elektromágneses
jelenségeken alapul. Feltételezték, hogy a
-nak negatív paritást adott.
Tsung-Dao Lee és Chen-Ning Yang (1. ábra) a
fenti kérdés megoldását keresve 50 évvel ezelőtt megvizsgálta
[2] a paritásmegmaradás kísérleti bizonyítékait
és megállapította, hogy valamennyi elektromágneses
jelenségeken alapul. Feltételezték, hogy a 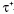 és
a
és
a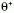 ugyanaz a részecske (azt ma K+ mezonnak hívjuk),
viszont a gyenge kölcsönhatás sérti a paritásmegmaradást,
és javasoltak néhány kísérletet a paritássértés
ellenőrzésére. A kísérleti ellenőrzés azonnal
megkezdődött, és igazolta a paritássértést; Lee és
Yang még 1957-ben megkapta a Nobel-díjat. (Elfilozofálhatunk
azon, hány cikk kell a Nobel-díjhoz: általában
egy, ha az elég jó.)
Az első kísérlet Chien-Shiung Wu asszony (1. ábra)
nevéhez fűződik [3]. 60Co izotópot mágneses térbe
helyezve lehűtöttek csaknem az abszolút zérus hőmérsékletre
(0,1 K alá). A 60Co mag instabil, béta-bomlással
a 60Ni izotóp gerjesztett állapotává alakul, azaz egyik
neutronja protonra, elektronra és antineutrínóra bomlik:
ugyanaz a részecske (azt ma K+ mezonnak hívjuk),
viszont a gyenge kölcsönhatás sérti a paritásmegmaradást,
és javasoltak néhány kísérletet a paritássértés
ellenőrzésére. A kísérleti ellenőrzés azonnal
megkezdődött, és igazolta a paritássértést; Lee és
Yang még 1957-ben megkapta a Nobel-díjat. (Elfilozofálhatunk
azon, hány cikk kell a Nobel-díjhoz: általában
egy, ha az elég jó.)
Az első kísérlet Chien-Shiung Wu asszony (1. ábra)
nevéhez fűződik [3]. 60Co izotópot mágneses térbe
helyezve lehűtöttek csaknem az abszolút zérus hőmérsékletre
(0,1 K alá). A 60Co mag instabil, béta-bomlással
a 60Ni izotóp gerjesztett állapotává alakul, azaz egyik
neutronja protonra, elektronra és antineutrínóra bomlik:
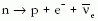 .
Mivel a 60Co S = 5, a 60Ni S = 4, a
kirepülő elektron és antineutrínó pedig S = 1/2 spinnel
rendelkezik, a megmaradási törvények előírják, hogy a
végállapoti részecskék impulzusmomentuma a 60Co-é
irányába mutasson (2. ábra). A mágneses tér a 60Co impulzusmomentumát
beállítja, a hűtés pedig a rezgését
minimalizálja, a kirepülő elektron impulzusmomentuma
(spinje) tehát a mágneses tér irányába fog mutatni.
A neutrínó spinje, elhanyagolhatóan kicsi tömege miatt,
párhuzamos az impulzusával. A paritásmegmaradás itt
tükörszimmetriát feltételez, akkor tehát az elektronok
valamennyi irányban egyforma valószínűséggel repülnek,
annak sértése viszont valamelyik irányt előnyben
fogja részesíteni.
Az eredmény megdöbbentette a fizikusvilágot: az
elektronok túlnyomórészt a mágneses térrel ellenkező
irányban léptek ki (2. ábra), ami azt jelentette, hogy a
gyenge kölcsönhatás maximálisan sérti a tükörszimmetriát
és a paritás megmaradását:
a mozgásiránnyal szemben
(balra) polarizált részecskéket
és a mozgásirányban
(jobbra) polarizált antirészecskéket
részesíti előnyben. Wolfgang
Pauli az eredmény hallatán
kijelentette: Nem tudom
elhinni, hogy Isten balkezes!
Az ugyancsak a Columbia egyetemen
dolgozó Leon Lederman
csoportja, hallván a
Wu-kísérlet első eredményeiről,
sokkal egyszerűbb mérésbe
kezdett [4]. Pozitív pionokat
állítottak meg szénben. A
pionok gyenge kölcsönhatásban
elbomlanak müonok kibocsátásával,
.
Mivel a 60Co S = 5, a 60Ni S = 4, a
kirepülő elektron és antineutrínó pedig S = 1/2 spinnel
rendelkezik, a megmaradási törvények előírják, hogy a
végállapoti részecskék impulzusmomentuma a 60Co-é
irányába mutasson (2. ábra). A mágneses tér a 60Co impulzusmomentumát
beállítja, a hűtés pedig a rezgését
minimalizálja, a kirepülő elektron impulzusmomentuma
(spinje) tehát a mágneses tér irányába fog mutatni.
A neutrínó spinje, elhanyagolhatóan kicsi tömege miatt,
párhuzamos az impulzusával. A paritásmegmaradás itt
tükörszimmetriát feltételez, akkor tehát az elektronok
valamennyi irányban egyforma valószínűséggel repülnek,
annak sértése viszont valamelyik irányt előnyben
fogja részesíteni.
Az eredmény megdöbbentette a fizikusvilágot: az
elektronok túlnyomórészt a mágneses térrel ellenkező
irányban léptek ki (2. ábra), ami azt jelentette, hogy a
gyenge kölcsönhatás maximálisan sérti a tükörszimmetriát
és a paritás megmaradását:
a mozgásiránnyal szemben
(balra) polarizált részecskéket
és a mozgásirányban
(jobbra) polarizált antirészecskéket
részesíti előnyben. Wolfgang
Pauli az eredmény hallatán
kijelentette: Nem tudom
elhinni, hogy Isten balkezes!
Az ugyancsak a Columbia egyetemen
dolgozó Leon Lederman
csoportja, hallván a
Wu-kísérlet első eredményeiről,
sokkal egyszerűbb mérésbe
kezdett [4]. Pozitív pionokat
állítottak meg szénben. A
pionok gyenge kölcsönhatásban
elbomlanak müonok kibocsátásával,
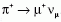 . A müonok polarizáltan keletkeznek:
mivel a pion spinje zérus és a keletkező leptonoké
1/2, az impulzusmegmaradás miatt a müon és a
neutrínó spinje egymással szemben fog állni. A müon
bomlása is gyenge kölcsönhatás,
. A müonok polarizáltan keletkeznek:
mivel a pion spinje zérus és a keletkező leptonoké
1/2, az impulzusmegmaradás miatt a müon és a
neutrínó spinje egymással szemben fog állni. A müon
bomlása is gyenge kölcsönhatás, 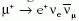 és ha
nincs tükörszimmetria, a pozitronok a müon polarizációs
irányában fognak kilépni. A müonok mágneses
térben precesszálnak, azaz a spinjük kis mágnesként
forog, a pozitronokat tehát a tükörszimmetria sértése
esetén a rögzített helyzetű detektor időben változó
intenzitással észleli. Amint a 3. ábra mutatja, a kilépő
pozitronok valóban a müon spinjének irányát követik,
a paritás tehát nem marad meg ebben az esetben sem.
A Lederman-kísérlet néhány nap alatt igazolta a
paritássértés elméletét, a szerzők azonban nem közölték
eredményüket addig, amíg a Wu-csoport is el nem
készült. Így a két cikk, [3] és [4] a
Physical Review
ugyanazon számában, egymást követve jelent meg;
Wuék Lee-nek és Yangnak mondtak köszönetet az
elméletért, míg Ledermanék Lee-nek az elmélet elmagyarázásáért
és Wunak előzetes eredménye közléséért.
Nem sokkal később Telegdi Bálint kísérlete is
igazolta a gyenge kölcsönhatás paritássértését.
A Lederman-kísérlet messzemenően túlmutatott a
paritássértés igazolásán: nemcsak sikerült megmérniük
a müon mágneses momentumát, de alapjául
szolgált a ma már széles körben elterjedt szilárdtestfizikai-
kémiai vizsgálati módszernek, a µSR-nek. A rövidítés
jelentése hármas: müonspin-rezonancia, -rotáció
és -relaxáció. A módszer elve az, hogy a polarizált
müonok precessziós frekvenciája,
és ha
nincs tükörszimmetria, a pozitronok a müon polarizációs
irányában fognak kilépni. A müonok mágneses
térben precesszálnak, azaz a spinjük kis mágnesként
forog, a pozitronokat tehát a tükörszimmetria sértése
esetén a rögzített helyzetű detektor időben változó
intenzitással észleli. Amint a 3. ábra mutatja, a kilépő
pozitronok valóban a müon spinjének irányát követik,
a paritás tehát nem marad meg ebben az esetben sem.
A Lederman-kísérlet néhány nap alatt igazolta a
paritássértés elméletét, a szerzők azonban nem közölték
eredményüket addig, amíg a Wu-csoport is el nem
készült. Így a két cikk, [3] és [4] a
Physical Review
ugyanazon számában, egymást követve jelent meg;
Wuék Lee-nek és Yangnak mondtak köszönetet az
elméletért, míg Ledermanék Lee-nek az elmélet elmagyarázásáért
és Wunak előzetes eredménye közléséért.
Nem sokkal később Telegdi Bálint kísérlete is
igazolta a gyenge kölcsönhatás paritássértését.
A Lederman-kísérlet messzemenően túlmutatott a
paritássértés igazolásán: nemcsak sikerült megmérniük
a müon mágneses momentumát, de alapjául
szolgált a ma már széles körben elterjedt szilárdtestfizikai-
kémiai vizsgálati módszernek, a µSR-nek. A rövidítés
jelentése hármas: müonspin-rezonancia, -rotáció
és -relaxáció. A módszer elve az, hogy a polarizált
müonok precessziós frekvenciája,
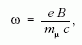
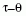 paradoxon tehát megoldódott,
a két részecske azonosnak bizonyult és
K-mezon (kaon) lett a neve. Négyféle
állapota van: K+, K-, K0 és anti-K0
(
paradoxon tehát megoldódott,
a két részecske azonosnak bizonyult és
K-mezon (kaon) lett a neve. Négyféle
állapota van: K+, K-, K0 és anti-K0
(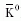 )
Az elektromosan semleges K0,
)
Az elektromosan semleges K0, 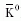 részecskék egyedülálló lehetőséget kínálnak
a CP-szimmetria megmaradásának ellenőrzésére.
Ha igaz a CP-szimmetria, akkor pozitív(negatív) CP-sajátállapot
pozitív(negatív) CP-sajátállapotba bomlik.
A K0 és
részecskék egyedülálló lehetőséget kínálnak
a CP-szimmetria megmaradásának ellenőrzésére.
Ha igaz a CP-szimmetria, akkor pozitív(negatív) CP-sajátállapot
pozitív(negatív) CP-sajátállapotba bomlik.
A K0 és 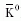 részecskék egyike sem CP-sajátállapot,
CPK0
részecskék egyike sem CP-sajátállapot,
CPK0 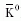 . (A CP-tükrözés itt egy a jelen cikk témá-
ján kívül eső, egyedül az erős kölcsönhatás által "tiszteletben
tartott" kvantumszám, a "ritkaság" előjelét
változtatja az ellenkezőjére.) CP-sajátállapotok a kettő
kombinációi lesznek:
. (A CP-tükrözés itt egy a jelen cikk témá-
ján kívül eső, egyedül az erős kölcsönhatás által "tiszteletben
tartott" kvantumszám, a "ritkaság" előjelét
változtatja az ellenkezőjére.) CP-sajátállapotok a kettő
kombinációi lesznek:
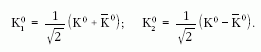

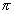 Decay of the
Decay of the
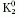 Meson, Physical Review Letters 13 (1964)
138-140
Meson, Physical Review Letters 13 (1964)
138-140