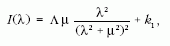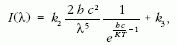Fizikai Szemle 2007/7. 225.o.
KÖVESLIGETHY RADÓ ÉS A TESTEK HŐMÉRSÉKLETI
SUGÁRZÁSA - EGY TUDOMÁNYTÖRTÉNETI ÉRDEKESSÉG
Slíz Judit, Rajnai Renáta
ELTE, TTK
Max Planck még el sem kezdett a feketetest-sugárzással
foglalkozni, amikor 1885. október 19-én a Magyar
Tudományos Akadémia osztályülésén Konkoly
Miklós miniszteri tanácsos felolvasta Kövesligethy
Radónak a Folytonos spektrumok elmélete című dolgozatát.
A dolgozatban Kövesligethy - 15 évvel a fény
kvantumos természetének felfedezése előtt - egy
olyan képlet levezetését mutatta be a hőmérsékleti
sugárzásra, amely - a forró csillagokat kivéve - mind
a mai napig jobban közelíti a csillagok intenzitásának
hullámhosszfüggését, mint a Planck-képlet.
Planck 1900. október 19-én, pontosan 15 évvel
Kövesligethy dolgozatának felolvasása után, a Berlini
Fizikai Társaság ülésén terjesztette elő a feketetest sugárzásra
vonatkozó híres képletét.
Wien, Rayleigh, Jeans és Planck vajon tudtak-e
Kövesligethy eredményeiről? Nem valószínű, mert
amikor saját eredményeikkel előrukkoltak, Kövesligethy
nevét sehol sem említik, és ekkor ő már rég nem
csillagászattal és hőmérsékleti sugárzással, hanem
szeizmológiával foglalkozott.
Ki is volt Kövesligethy Radó?
1862-ben született az akkor osztrák fennhatóság alatt
álló Veronában. Feltételezhetően gyermekkorának
egy részét Augsburgban töltötte, azt viszont pontosan
tudjuk, hogy elemi iskoláit Bajorországban, gimnáziumi
tanulmányait Pozsonyban végezte.
19 évesen a bécsi egyetemre jelentkezett, ahol elméleti
fizikát, csillagászatot és asztrofizikát tanult.
Ekkor már 21 idegen nyelvű cikke volt. Talán mozgalmas
gyerekkorának, valamint jó eszének és eleven
érdeklődésének tudható be, hogy egyformán jól beszélt
magyarul, olaszul, franciául, angolul és németül,
de a latin és a görög nyelvet is ismerte.
1882-től a bécsi csillagvizsgáló segédje, 1882-től
1887-ig pedig Konkoly Thege Miklós ógyallai magánobszervatóriumában
dolgozott. 1888 őszétől Eötvös
Loránd tanársegédje Pesten. 1893. augusztus 6-án
nyilvános rendkívüli tanári címet kapott. Főleg színképelemzéssel
foglalkozott, az ógyallai színképkatalógus
adatainak nagy része tőle származik. Doktori
értekezésében megkísérelte a sugárzó test hőmérsékletének
és a folytonos színkép hullámhossz szerinti fényességeloszlásának
összefüggését kimutatni
(1884). Utóbb ezt az elméletét továbbfejlesztve megkísérelte
a csillagok hőmérsékletének meghatározását
(1890), és a világon először kapott reális értékeket a
hideg csillagok felszíni hőmérsékletére.
1886-tól a kiskartali Podmaniczky-féle magán-csillagvizsgáló
felügyelője. A nyírmadai Dégenfeld-kastély
udvarán fedezte fel Podmaniczkyné Dégenfeld-Schomburg
Bertával az első ismert extragalaktikus szupernóvát
(S Andromedae, 1885. augusztus 22., 1. ábra).
1888-tól a Tudományegyetem kísérleti fizikai intézetének
asszisztense, 1889-ben a kozmográfia és a
geofizika magántanára, 1897-től a kozmográfia rendkívüli tanára,
majd az intézet vezetője. A hazai csillagászati oktatást
nemzetközi színvonalra emelte.
Érdeklődését a százhúszezer áldozatot követelő
1908-as messinai földrengés véglegesen - Kosztolányi
szavaival - a "vak csillag", azaz a Föld felé fordította.
Eljárásokon törte a fejét, hogyan lehetne előrejelzéssel
megakadályozni ezeket a nagy katasztrófákat. Egyre
többet foglalkozott szeizmológiával, kidolgozta a földrengéserősség
számszerű, egzakt definiálási skáláját,
majd először adott matematikai módszert a földrengések
fészekmélységének kiszámítására. 1904-től a Nemzetközi Földrengési Szövetség
állandó tagja. 1906-ban
megalapította Budapesten a Magyar Földrengés Számláló
Intézetet és az egyetemi Földrengési Obszervatóriumot,
amelynek haláláig igazgatója volt.
Nagy nyelvismerete révén széles körű nemzetközi
kapcsolatokat épített ki, és a tudományos ismeretterjesztést
is magas színvonalon művelte. Sokoldalú,
színes egyéniség volt, szívesen foglalkozott szépirodalommal
is. Ódákat írt görögül, és egy színdarabja is
fennmaradt Szférák zenéje címmel.
1934-ben halt meg Budapesten.

A Kövesligethy-képlet
és összehasonlítása
a Planck-formulával
Kövesligethy tisztán termodinamikai
úton jutott eredményéhez
- hasonlóan, mint Wien,
Rayleigh és Jeans -, de az ő
képlete minden hullámhosszon
jó közelítést ad.
A fény kvantumos természetéről
még semmit sem tudván
megállapítja, hogy a testek
sugárzásának intenzitása
arányos a test rezgő anyagi
részecskéinek mozgási energiájával,
melyet átadnak az
éterrészecskéknek, a fény pedig
az így megrezgetett éterrészecskékben
a rezgés terjedése.
Ebből kiindulva levezetett egy képletet a sugárzó
testek intenzitásának hullámhosszfüggésére, amelyet
a Napra kalibrálva kipróbált, és amelyről később
kiderült, hogy a korai típusú (O és B) csillagokat kivéve
jobb közelítést ad, mint a Planck-képlet.
A képlet részletes levezetése megtalálható a Magyar
Tudományos Akadémiának az Értekezések a mathematikai
tudományok köréből című kiadványa 12.
kötetében, amely Budapesten jelent meg 1886-ban.
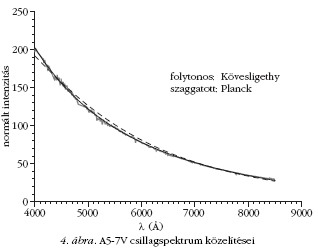
És most lássuk a Kövesligethy-féle képletet és öszszehasonlítását
a Planck-féle képlettel különféle spektráltípusú
csillagokra. A csillagszínképeket a
http://zebu.uoregon.edu/spectrar.html internetes oldalról töltöttük
le. Hat fősorozati csillagot választottunk ki, minden
színképtípusból egyet-egyet1. A képleteket
a spektrumok kontinuumának közelítésére használtuk. Az
eredmények a következők:
Kövesligethy képlete
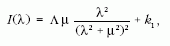
λ a hullámhossz, Λ konstans, µ a maximális intenzitás
hullámhossza és k1 az intenzitás skálájától függő
konstans.
Planck képlete
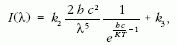
λ a hullámhossz, k2, k3 az intenzitás skálájától függő
konstansok, h = 6,626 · 10-34 m2kg / s, c = 3 · 108 m / s
(Planck-állandó), k = 1,3806505 · 10-23 m2kg / s2K
(Boltzmann-állandó) és T a felületi hőmérséklet.
1. táblázat
Kövesligethy-féle közelítés
|
| színképosztály | O5V | B6V | A5-7V |
F6-7V | G1-2V | K4V |
| λ (J/s) | 1,254 · 1010 | 35 · 108 |
108 | 2,357 · 106 |
2,937 · 106 | 8,1 · 106 |
| µ (Â) | 0,79 | 1,5 | 36,0 | 3567,0 |
4307,0 | 6455,0 |
| k1 | -164,09 | -68,0 | 233,0 |
-39,62 | -62,43 | -207,0 |
szórásnégyzet | 735,269 | 79,953 | 2,085
| 5,376 | 7,754 | 9,176 |
2. táblázat
Planck-féle közelítés
|
| színképosztály | O5V | B6V | A5-7V |
F6-7V | G1-2V | K4V |
| Teff (K) | 33 880 | 26 723 | 10 555
| 8 100 | 7 348 | 4 567 |
| k3 | -28,79 | 0 | -69,0
| 18,44 | 25,9 | -37,0 |
| k2 | 0,089 | 7,0 | 50,0
| 0,847 | 1,0 | 1764,0 |
| szórásnégyzet | 159,024 | 13,389 | 9,484
| 21,668 | 17,562 | 12,944 |
A Kövesligethy-képlet a maximális intenzitás helyét
adja meg közvetlenül, míg Planck képlete a csillag
hőmérsékletét. Mindkettő csak közelítés.
Mindezt az 1-2. táblázatokban és 2-7. ábrákon
mutatjuk be.
Az eredmények elemzése
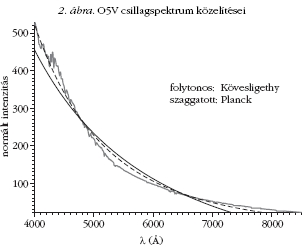
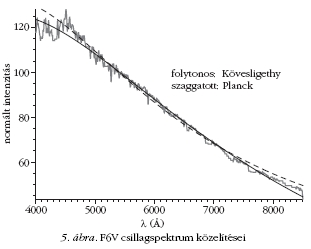
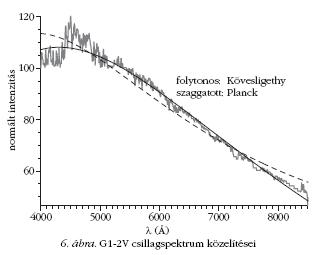
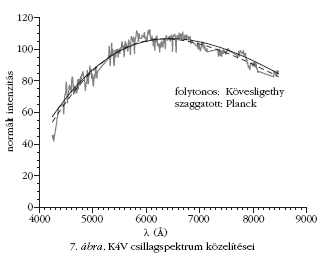
A forróbb (O5V, B6V) csillagokat kivéve mindenütt
jobb a kontinuum közelítésére Kövesligethy egyszerűen
kezelhető képlete, így akár ma is lehet használni
erre a célra. Megjegyezzük, hogy az O5V típusú csillagnál
a Planck-görbe sem ad túl jó közelítést. Mint
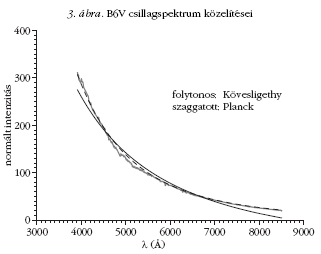
ahogy az ábrákon és a táblázatokból is látszik, az
A5-7V típusú csillagnál a legjobb a közelítés mind
Planck, mind Kövesligethy képletével.
3. táblázat
A Kövesligethy- és Planck-féle képlettel számolt
intenzitásmaximum-helyek |
| csillagtípus |
T (K) |
λ max (Â) |
eltérés
(%) |
| Planck | Kövesligethy |
| F6-7V | 8 100 | 3 576 | 3 567 | 0,25 |
| G1-2V | 7 348 | 3 942 | 4 307 | 9,26 |
| K4V | 4 567 | 6 343 | 6 455 | 1,77 |
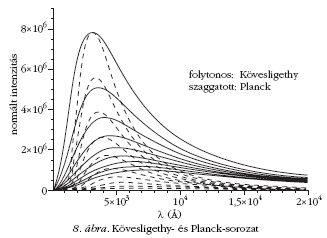
Kövesligethy zseniális képlete az intenzitás maximumának
Eltolódási törvényét is magában foglalja. Ez
jól látható a 8. ábrán.
Ha összehasonlítjuk a Planck-függvényből a Wien-féle
összefüggés alapján a maximális intenzitáshoz tartozó
hullámhosszakat a Kövesligethy-képletből származókkal,
érdekes dolgot tapasztalunk az F6-7V,
G1-2V és K4V típusú csillagok esetén (3. táblázat ).
A táblázatból jól látható, hogy az F6-7V és a K4V
típusú csillag esetében alig van eltérés (0,25%,
1,77%) a maximális intenzitáshoz tartozó hullámhosszak
között a kétféle közelítésben. Tehát az 1886-ban
közzétett Kövesligethy-féle képlet a csillagspektrumok
maximumhelyeinek megtalálására is kiválóan
alkalmas.
________________________________
A szerzők csillagász hallgatók
1 Az oldalon David R. Silva: A new Library of Stellar Optical Spectra
című cikkében közölt csillagspektrumok találhatók. A cikk The
Astrophysical Journal Supplement Series folyóirat 81. kötetének 865-881.
oldalán jelent meg 1992 augusztusában.