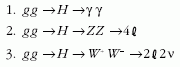Fizikai Szemle 2007/8. 253.o.
A STANDARD MODELL HIGGS-BOZONJA
NYOMÁBAN AZ LHC-NÁL
Trócsányi Zoltán
Debreceni Egyetem és
MTA Atommagkutató Intézete, Debrecen
Négy alapvető kölcsönhatást ismerünk: a tömegvonzást,
az elektromágneses, a gyenge és az erős kölcsönhatásokat.
Az elemi részecskék általunk eddig
vizsgált világában az utóbbi háromnak van lényeges
szerepe.Ezek egységes elméleti keretbe foglalhatók:
az elemi részek Standard Modellje a részecskék mindhárom
kölcsönhatását leírja. A Standard Modell olyan
kvantumtérelméletekre alapul, amelyben a fizikai
terek bizonyos szabadsági fokainak értéke a geometriai
tér különböző pontjaiban egymástól függetlenül,
szabadon választható meg. Az ilyen elméleteket mértékelméleteknek
nevezzük, a választási szabadságból
fakadó szimmetriát mértékszimmetriának. A mértékszimmetrikus
elméletek legegyszerűbb példája a
kvantum-elektrodinamika (QED), amelyben az elektrontér,
azaz egy komplex spinortér fázisa választható
szabadon, annak értékétől fizikailag mérhető mennyiségek
nem függnek. A szabad fázisválasztás leírható a
térnek egy U(1) csoportelemmel (egydimenziós unitér
mátrix, azaz egy komplex fázis) való szorzásaként.
A Standard Modell kiinduló szimmetriája a
G = SU(3)C× SU(2)L
× U(1)Y
csoportelemek szerinti transzformációkkal szembeni
szimmetria. Az SU(3)C mértékszimmetria következménye
a kvarkok közötti erős kölcsönhatás. A szimmetria
a kvarkok három, az egyszerűbb szóhasználat kedvéért
színnek (colour) nevezett, C szabadsági fokának
a szabadon választhatóságát jelenti. Az
SU(2)L × U(1)Y
szimmetria egyesíti az elektromágneses és gyenge
kölcsönhatásokat az elektrogyenge elméletbe. Az L
szabadsági fok két értéket vehet fel, ezért a fermionok
spinjének mintájára gyenge izospinnek nevezik. Az L
arra utal, hogy csak a balkezes (left) fermionok, amelyeknél
a lendületvektor és a spin ellentétes irányúak,
rendelkeznek gyenge izospinnel. A jobbkezesek az
SU(2) transzformáció esetén nem változnak. Az U(1)Y
szimmetria a fermionok szabad fázisválasztását jelenti.
Az elektromágneses U(1)EM szimmetriától csak
annyiban különbözik, hogy a szimmetria következményeként
nem az elektromos töltés, hanem az Y
gyenge hipertöltés marad meg (a Standard Modellben
a gyenge izospin harmadik komponense sajátértékének
és a hipertöltésnek az összege az elektromos töltés
Q = T 3 + Y).
A modellben három fermioncsalád van, mindegyikben
15 fermionnal - három leptonnal és 12 kvarkkal.
Az első családban találjuk az SU(2) dublettet alkotó
balkezes elektront és a neutrínóját, a jobbkezes elektront,1
valamint bal- és jobbkezes u és d kvarkokat, az
utóbbiakat egyenként három szín szabadsági fokkal.
A másik két család az elsőnek pontos mása, csak a
részecskék tömege nagyobb. A bennük található fermionokat
és azok SU(N) ábrázolásának dimenzióit és
kvantumszámait az 1. táblázat tartalmazza.
Az elmélet kialakulásához vezető úton az első lépést
Fermi tette meg, aki az 1930-as években a gyenge
kölcsönhatás négy-fermion modelljét tisztán fenomenologikus
úton megalkotta az akkor kialakuló
QED mintájára. A továbblépéshez már elméleti megfontolások
vezettek. Kiderült, hogy a Fermi-elméletben
nem lehet következetesen számítani a magasabbrendű
perturbatív járulékokat (sugárzási korrekciókat),
továbbá nagyenergiájú elektron-neutrínó
szórásban sérül az unitaritás (az ütköző részecskék
energiájának növelésével a folyamat valószínűsége
egynél nagyobbá válik). Az elméleti
problémák megoldása a mértékszimmetria, mint
alapelv segítségével vált lehetővé.
A G mértékcsoportra alapuló Standard Modell
szép, gazdaságos és a mérési adatok nagypontosságú
leírását szolgáltatja. Az elektron-pozitron
ütközésekben mérhető mennyiségeknek a
Standard Modellel számolt, valamint a Nagy
Elektron-Pozitron gyorsítónál (LEP) mért értékei
közötti egyezés rendkívül meggyőző, ami a
Standard Modell fizikai helyességét sugallja.
A LEP-gyorsítón közvetlenül lehetett ellenőrizni
az elektrogyenge mértékszimmetriát az
e+e- → W+W-
folyamat végállapotában található
longitudinálisan polarizált mértékbozonok keletkezési
hatáskeresztmetszetének tanulmányozásával.
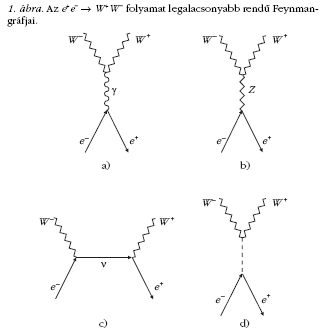
A J = 1 parciális hullámban a perturbációszámítás
vezető rendjében az 1. a-c ábrák
Feynman-gráfjai által mutatott folyamatok járulnak
hozzá a szórási amplitúdóhoz.
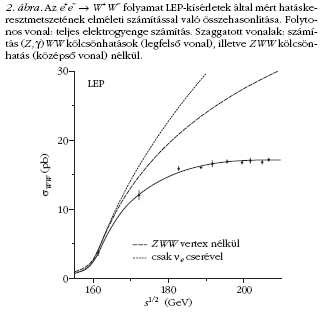
A gráfok alapján számolt, sugárzási korrekciókkal
javított hatáskeresztmetszetnek a LEP-nél mért értékekkel
való összehasonlítását mutatja a 2. ábra.
Ugyanott megtaláljuk a ZWW-kölcsönhatás elhagyásával
kapott számítás, valamint a gyenge mértékbozonok
közötti összes kölcsönhatás elhagyásával kapott
számítás eredményét. A mérési eredmények világosan
a teljes elektrogyenge modellel kapott számítást támasztják
alá.
A J = 0 parciális hullám esetén azonban az 1. a-c
ábrák gráfjaiból számolt W-párkeltési valószínűség
növekvő tömegközépponti energia esetén növekszik,
és egynél nagyobbá is válhat, amit úgy mondunk,
hogy sérül az unitaritás.Ezt a képtelenséget feloldhatjuk,
ha feltesszük egy H skalár részecske létezését,
amely mind a leptonokkal, mind a mértékbozonokkal
kölcsönhat. Az 1.d ábrán mutatott folyamat járuléka
megszünteti az unitaritás sérülését. De vajon létezik-e
a H részecske a természetben?
A Standard Modell szimmetriája közvetlenül nem
tapasztalható a valóságban.Tömeggel rendelkező
részecskéket leíró elmélet ugyanis nem lehet
SU(2)L × U(1)Y szimmetrikus, a tapasztalat szerint
azonban az összes fermion, továbbá a mértékterek elemi
gerjesztései közül három tömeggel rendelkezik. A
valóságban csak az erős kölcsönhatást közvetítő gluontér
elemi gerjesztései és a foton nem rendelkeznek
nyugalmi tömeggel, azaz csak SU(3)c × U(1)EM szimmetriát
észlelünk. A mai részecskefizika legfontosabb válaszra
váró kérdése, hogy hogyan marad rejtve az elektrogyenge
szimmetria, mi az SU(3)c × SU(2)L × U(1)Y
→ SU(3)c × U(1)EM szimmetriasérülés oka, amit úgy is
szoktak fogalmazni, "Honnan nyerik az elemi részecskék
tömegüket?"2
A modell szép megoldást kínál erre a kérdésre is. A
szupravezetés Ginzburg-Landau-elméletének relativisztikus
általánosításával néhányan egymástól függetlenül
javasolták azt a modellt, amely végül Higgsmechanizmusként
rögzült a részecskefizikában. A
modell lényege, hogy a természeti törvények szimmetriája
nem jelenti azt, hogy a szimmetriát a megfigyelhető
jelenségeknek is tükrözni kell.Például a
Lagrange-függvény szintjén meglévő szimmetriát a
rendszer alapállapota (részecskefizika esetén ez a
vákuum) sérti.Ez a jelenség a spontán szimmetriasértés.
Az elektrogyenge elméletben ezt úgy valósítjuk
meg, hogy bevezetünk egy SU(2)-dublett, komplex
skalárteret,
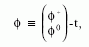 | (1) |
(1,2,1/2) szín-, gyenge izospin- és hipertöltés kvan-
tumszámokkal. A Q = T3+Y összefüggés alapján a
skalártér felső komponense +1 elemi töltéssel rendelkezik,
míg az alsó komponens semleges. A skalártér
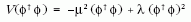 | (2) |
(µ, λ valósak, λ > 0) potenciáljának végtelen sok
minimuma van a 3. ábrán mutatott helyeken. Alapállapotban
a rendszer ezek közül véletlenszerűen egyet
kiválaszt, amely a mértékszimmetria felhasználásával
megszorítás nélkül
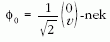 | (3) |
választható. A vákuum invariáns a 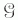 generátorhoz
(Pauli-mátrixok, illetve a 2 × 2-es egységmátrix) tartozó
U =
generátorhoz
(Pauli-mátrixok, illetve a 2 × 2-es egységmátrix) tartozó
U = 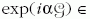 G transzformációval szemben, ha
UΦ0 = Φ0, ahonnan
G transzformációval szemben, ha
UΦ0 = Φ0, ahonnan 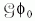 = 0
következik. Gyors számítás
mutatja, hogy ez egyik csoportgenerátorral sem
teljesül, de az elektromos töltésre igen, tehát a vákuum
az eredeti SU(3)c × SU(2)L × U(1)Y szimmetriát
SU(3)c × U(1)EM szimmetriára sérti.
Természetesen a skalárteret tartalmazó elméletnek
is G-invariánsnak kell lennie, amelynek következményeként
a kölcsönhatást közvetítő mértékbozonok a
fermionokon kívül a skalártérrel is kölcsönhatnak. A
szimmetriasérülés eredményeként a skalártér alapállapotával,
a vákuummal való kölcsönhatás a gyenge
mértékbozonoknak a v vákuum várhatóértékkel arányos
tömeget ad. A Φ0 alapállapot körül
= 0
következik. Gyors számítás
mutatja, hogy ez egyik csoportgenerátorral sem
teljesül, de az elektromos töltésre igen, tehát a vákuum
az eredeti SU(3)c × SU(2)L × U(1)Y szimmetriát
SU(3)c × U(1)EM szimmetriára sérti.
Természetesen a skalárteret tartalmazó elméletnek
is G-invariánsnak kell lennie, amelynek következményeként
a kölcsönhatást közvetítő mértékbozonok a
fermionokon kívül a skalártérrel is kölcsönhatnak. A
szimmetriasérülés eredményeként a skalártér alapállapotával,
a vákuummal való kölcsönhatás a gyenge
mértékbozonoknak a v vákuum várhatóértékkel arányos
tömeget ad. A Φ0 alapállapot körül
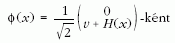 | (4) |
parametrizálva a teret, a modell tartalmaz egy nulla
spinű semleges skalárteret, a H(x) Higgs-teret, amelynek
elemi gerjesztése, a Higgs-bozon, kölcsönhat a
gyenge kölcsönhatást közvetítő mértékbozonokkal. A
kölcsönhatás erőssége arányos a mértékbozonok tömegének
négyzetével. A Higgs-mechanizmus szépsége,
hogy a mértékszimmetria fenntartásával a fermionoknak
is lehet tömegtagokat generálni. A fermionok
szintén kölcsönhatnak a Higgs-bozonnal, a kölcsönhatás
erőssége a fermionok tömegével arányos.
A Standard Modell fenomenológiai sikere azt sugallja,
hogy az elektrogyenge szimmetriasértés egy a
Fermi-skálán működő újfajta alapvető kölcsönhatásnak
köszönhető.Egyelőre azonban fogalmunk sincs
arról, miféle erő ez. A Nagy Hadronütköztető (LHC)
építésének elsődleges célja az új erő felderítése.
A leggazdaságosabb lehetőség, hogy az elektrogyenge
szimmetriasértésért egy komplex skalártér felelős.
Láttuk, hogy ekkor az elmélet megjósolja egy semleges
skalártér elemi gerjesztésének, a Higgs-bozonnak a létét,
azonban nem tud becslést adni a Higgs-bozon tömegére,
valamint a fermionokkal való csatolásának
erősségére. A részecskefizika előtt álló legfontosabb
feladat tehát választ keresni a következő kérdésekre:
- Létezik-e valóban a Higgs-bozon? Ha igen, hány
fajtában?
- Melyek a kvantumszámai?
- Valóban egyszerre ad tömeget a Higgs-tér a vektorbozonoknak
és a fermionoknak?
- Hogyan hat a Higgs-tér önmagával kölcsön?
Ezek a kérdések már érett középkorba léptek, ezért
részletes eljárásokat dolgoztak ki, hogy az LHC-nál
választ kapjunk rájuk. Az írás további részében csak
az elsővel foglalkozunk: áttekintjük, hogyan lehet a
Higgs-bozont nagyenergiájú elemirész-ütközésekben
észlelni. A Higgs-részecske keresése ahhoz hasonlítható,
mintha olyan tűt keresnénk a szénakazalban,
amelynek az alakjáról is csak feltevéseink vannak.
Az új részecske felfedezéséhez először a részecskét
elő kell állítani, ami Einstein E = mc2 egyenlete alapján
lehetséges.Ha egy részecske tömegének megfelelő
energiánál nagyobb energiát kis térrészre
koncentrálunk, akkor a részecske keletkezhet a rendelkezésre
álló energiából. A nagy energiakoncentráció tárológyűrűs
részecskeütköztetőkben történik. A LEP-gyorsítóban
elektron-pozitron ütközéseket hoztak létre
91-209 GeV tömegközépponti energián. A jelenleg is
működő Tevatronban 2 TeV energián proton-antiproton
ütközéseket hoznak létre. A 2008 májusában beinduló
LHC 14 TeV energián működő, proton-proton
ütközéseket létrehozó hadrongyorsító lesz.
Említettük, hogy a Higgs-bozonnak a fermionokkal való kölcsönhatása
a fermionok tömegével arányos. Az elektron
tömege nagyon kicsi, ezért az e+ e- → H folyamat
valószínűsége is nagyon kicsi. A LEP-gyorsítón a
Higgs-bozon előállításának legvalószínűbb módja a
nagyenergiájú Z bozonról való kisugárzás, a e+ e- → Z*
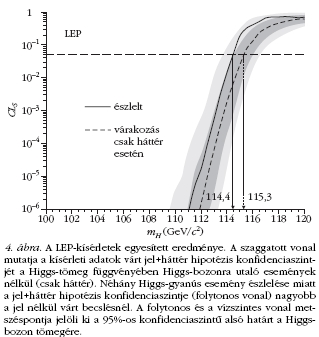
→ ZH → 4 fermion folyamat. A LEP-kísérletek nem találtak
Higgs-részecskét, ezért annak létezését majdnem
a kinematikai határig, pontosan 114,4 GeV/c2-ig
kizárták (4. ábra).
A hadrongyorsítókon az elemi ütközések könnyű
kvarkok (u és d) valamint gluonok között történnek.
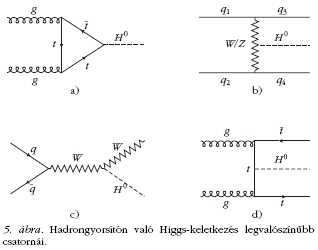
A Higgs keletkezésének legvalószínűbb módja az 5. a
ábrán mutatott gluon-gluon fúzió kvarkhurokba, és a
Higgs a nehéz kvarkról sugárzik.T ovábbi három lényeges
keltési mód az 5.b ábrán látható gyenge mértékbozon-
fúziós (WBF) keltés, az 5.c ábra kvark-antikvark
szétsugárzása gyors, Higgs-részecskét sugárzó
gyenge mértékbozonba, valamint a 5.d ábrán mutatott
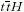 együttes keltés.
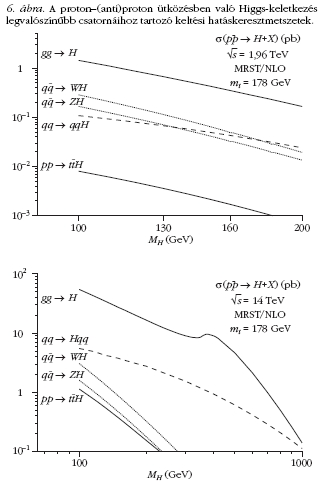
A 6. ábra mutatja a Tevatron- és LHC-energiákon
számolt keltési hatáskeresztmetszeteket a Higgstömeg
függvényében. Az LHC-n a 100 GeV-es energiatartományba
eső részecskék keltésében a gluonütközések
fognak lényeges szerepet játszani, így a
Higgs-keltés fő folyamata a gluonfúzió.
együttes keltés.
A 6. ábra mutatja a Tevatron- és LHC-energiákon
számolt keltési hatáskeresztmetszeteket a Higgstömeg
függvényében. Az LHC-n a 100 GeV-es energiatartományba
eső részecskék keltésében a gluonütközések
fognak lényeges szerepet játszani, így a
Higgs-keltés fő folyamata a gluonfúzió.
A Higgs-bozon a Standard Modell többi részecskéjénél
nehezebb (a LEP kizárási határ szerint csak a top
kvark lehet nehezebb nála) ezért a keletkezett Higgs
rögtön el is bomlik elsősorban nehéz részecskék párjaiba.
A Higgs tömegétől függ, hogy melyek a lényeges
bomlási csatornák, hiszen nemcsak a csatolás
erőssége, hanem a kinematikai küszöb is lényegesen
befolyásolja részecskepár keletkezésének valószínűségét.
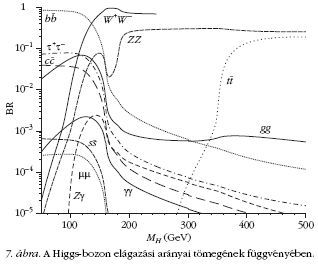
A 7. ábra mutatja a Higgs-bozon elágazási arányait
(a parciális bomlási szélesség aránya a teljes
bomlási szélességhez, Γi /Γtot) tömegének
függvényében. Látjuk, hogy a kis tömegek tartományától
eltekintve - ahol a 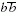 párba való bomlás a legvalószínűbb
-, a gyenge vektorbozonok uralják a Higgsbomlás
végállapotát. Vegyük észre, hogy kis valószínűséggel
ugyan, de nulla tömegű részecskék is lehetnek
a végállapotban: gg, Zγ, valamint γγ,, aminek a
továbbiakban lényeges szerepe lesz. A fontos következtetés
az, hogy a Higgs-részecske a tömegétől függően
más-más részecskékbe szeret elbomlani.Ebből
következik, hogy a felfedezéshez vezető keresési csatornák
is függenek a Higgs-tömegtől.
párba való bomlás a legvalószínűbb
-, a gyenge vektorbozonok uralják a Higgsbomlás
végállapotát. Vegyük észre, hogy kis valószínűséggel
ugyan, de nulla tömegű részecskék is lehetnek
a végállapotban: gg, Zγ, valamint γγ,, aminek a
továbbiakban lényeges szerepe lesz. A fontos következtetés
az, hogy a Higgs-részecske a tömegétől függően
más-más részecskékbe szeret elbomlani.Ebből
következik, hogy a felfedezéshez vezető keresési csatornák
is függenek a Higgs-tömegtől.
A Higgs-bozon nehéz a többi részecskéhez képest,
ezért az ütközési kísérletekben viszonylag ritkán keletkezik.
Más végállapotok valószínűsége sokkal nagyobb.
A 8. ábrán a proton-(anti)proton ütközésekben megjelenő
végállapotok hatáskeresztmetszetét látjuk a tömegközépponti
energia függvényében. Alacsonyabb energiákon
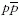 (Tevatron), magasabb energiákon pp (LHC)
ütközések hatáskeresztmetszetei láthatók (a 4 TeV-nél
látható szakadás mutatja a váltást). Azt látjuk, hogy a
Higgs-bozon keletkezésének valószínűsége nagyságrendekkel
kisebb más Standard Modell-beli folyamatok valószínűségénél.
A Higgs bomlástermékei ugyanazok a
részecskék, amelyek ezekben a más folyamatokban is
keletkeznek, ezért a Higgs-keletkezésre utaló jelet mindig
nagy háttér felett kell megtalálni.
A Higgs-keresés esetén a jel (S ) és háttér (B) viszonya
kétféle lehet: (i) a Higgs-bomlás eredményeként
keletkező részecskepár invariáns tömegeloszlásában
a Higgs-keletkezéshez tartozó rezonancia egy sima
háttéren ül, (ii) a Higgs-keletkezés jele és a háttér
alakja hasonló. Az első esetben a keresés tisztán kísérleti
úton sikeres lehet. A háttér jól meghatározható
a rezonancia két oldalán található eloszlásból, annak
levonásával a rezonanciacsúcs egyértelművé válik. A
siker feltétele, hogy a jel szignifikanciája, ami nagyjából
az S · B1/2 viszony, elegendően nagy legyen. Az
ötnél nagyobb érték a biztos felfedezés (99,999%-os
biztonságú) elfogadott szintje.
(Tevatron), magasabb energiákon pp (LHC)
ütközések hatáskeresztmetszetei láthatók (a 4 TeV-nél
látható szakadás mutatja a váltást). Azt látjuk, hogy a
Higgs-bozon keletkezésének valószínűsége nagyságrendekkel
kisebb más Standard Modell-beli folyamatok valószínűségénél.
A Higgs bomlástermékei ugyanazok a
részecskék, amelyek ezekben a más folyamatokban is
keletkeznek, ezért a Higgs-keletkezésre utaló jelet mindig
nagy háttér felett kell megtalálni.
A Higgs-keresés esetén a jel (S ) és háttér (B) viszonya
kétféle lehet: (i) a Higgs-bomlás eredményeként
keletkező részecskepár invariáns tömegeloszlásában
a Higgs-keletkezéshez tartozó rezonancia egy sima
háttéren ül, (ii) a Higgs-keletkezés jele és a háttér
alakja hasonló. Az első esetben a keresés tisztán kísérleti
úton sikeres lehet. A háttér jól meghatározható
a rezonancia két oldalán található eloszlásból, annak
levonásával a rezonanciacsúcs egyértelművé válik. A
siker feltétele, hogy a jel szignifikanciája, ami nagyjából
az S · B1/2 viszony, elegendően nagy legyen. Az
ötnél nagyobb érték a biztos felfedezés (99,999%-os
biztonságú) elfogadott szintje.
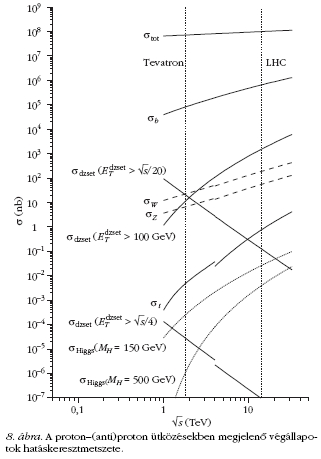
Tekintsük először a kis Higgs-tömegek tartományát!
Legkézenfekvőbbnek tűnhet a jel leggyakoribb
végállapotát (H → 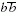 )
választani keresési csatornaként,
azonban ez esetben a jel elvész a hatalmas háttérben.
Minthogy hadronütköztetőn a hadronikus
végállapotok óriási túlsúlyban vannak, ezért az általános
ökölszabály szerint olyan végállapotokra érdemes
figyelni, amelyekben legalább egy nagy energiájú
lepton van a végállapotban. Ilyen esetekben a háttér
lényegesen kisebb, vagy megfelelő vágásokkal kisebbé
tehető. Az egyes keresési csatornák részletes vizsgálata
azt mutatja, hogy 30 fb-1 integrált luminozitás3
esetén a következő csatornák egyesített eredményei a
Standard Modell-beli Higgs-bozonnak a CMS detektoron
való biztos felfedezéséhez vezet az mH = 100-600
GeV/c2 tömegtartományban:
)
választani keresési csatornaként,
azonban ez esetben a jel elvész a hatalmas háttérben.
Minthogy hadronütköztetőn a hadronikus
végállapotok óriási túlsúlyban vannak, ezért az általános
ökölszabály szerint olyan végállapotokra érdemes
figyelni, amelyekben legalább egy nagy energiájú
lepton van a végállapotban. Ilyen esetekben a háttér
lényegesen kisebb, vagy megfelelő vágásokkal kisebbé
tehető. Az egyes keresési csatornák részletes vizsgálata
azt mutatja, hogy 30 fb-1 integrált luminozitás3
esetén a következő csatornák egyesített eredményei a
Standard Modell-beli Higgs-bozonnak a CMS detektoron
való biztos felfedezéséhez vezet az mH = 100-600
GeV/c2 tömegtartományban:
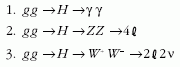
Érdekes módon a kis Higgs-tömeg tartományban
(mH ≤ 130 GeV/c2; a LEP-adatok szerint a legvalószínűbb
eset) az első a legígéretesebb folyamat. Bár az
elágazási arány kicsi, mintegy 2 ezrelék, az LHC-n a
gg &rarr H keltési csatorna hatáskeresztmetszete elegendően
nagy ahhoz, hogy bőséges számban találjunk
jelet γγ végállapottal. Kérdés azonban, hogy milyen a
háttér. Szerencsére az összes lehetséges háttér a γγ
pár invariáns tömegével fordított arányban csökken,
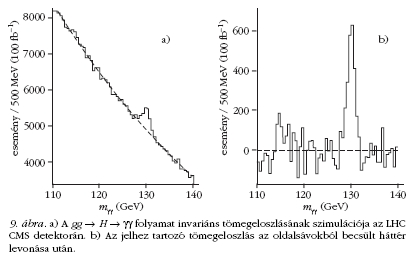
ezért a jel-háttér viszony első esete áll fenn. A 9. a
ábra mutatja a sima háttéren a Higgs-rezonanciát, az
ábra b) része pedig a rezonanciát az oldalakra illesztett
háttér levonása után.
A Higgs-bozon nem csatolódik közvetlenül a fotonokhoz,
hanem W- és t -kvark hurokhoz, amelyekről
a két foton kisugárzódik (lásd az 5. a ábrát jobbról
balra olvasva, a gluonokat fotonra cserélve, a hurokban
W-vel vagy t -vel). A kétfajta hurok járuléka egymást
nagyrészt kioltja. Két közel azonos szám kis különbségében
felerősödve jelenik meg valamelyik változása.
Ezért ha az új fizika akár a csatolásokat változtatja
kis mértékben, akár új hurokjárulékként jelenik
meg, jelentősen befolyásolhatja a γ (H → γγ) parciális
bomlási szélességet, amely így igen érzékeny az Standard
Modellbe nem illeszthető fizikára. A helyzetet
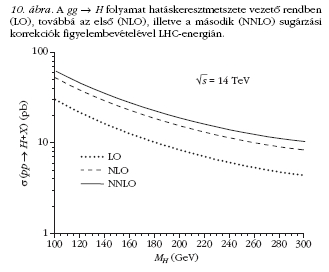
tovább bonyolítja, hogy a fő Higgs-keltési folyamat, a
gluon-gluon fúzió hatáskeresztmetszete jelentősen nő
a sugárzási korrekciók figyelembevételével (10. ábra
). Ha tehát a két-foton invariáns tömegének spektrumában
sikerül is részecskerezonanciát találni, még
további hosszas tanulmányokat igényel (ebben és a
többi csatornában) annak eldöntése, hogy milyen
részecskét is sikerült felfedezni.
Az LHC-n a 180 GeV/c²-nél nagyobb
tömegű Higgs keresése viszonylag
könnyű a pp → H → ZZ → 4l folyamatban.
Ebben a csatornában a Higgs-keltési
hatáskeresztmetszet nagy, néhányszor
tíz pikobarn (10. ábra ), a Higgs-elágazási
arány is jelentős (20-30%, 7. a
ábra ), és a Z bozon töltött leptonokba
való bomlásának valószínűsége mintegy
10% (LEP-adat).Ezek az értékek
önmagukban már 1 fb-1 integrált luminozitás
esetén elegendő eseményszámot
biztosítanának, azonban figyelembe
kell vennünk a lehetséges hátteret
is. Szerencsére hátteret lényegében
csak a jól értett pp → ZZ → 4l folyamatok
jelentenek.
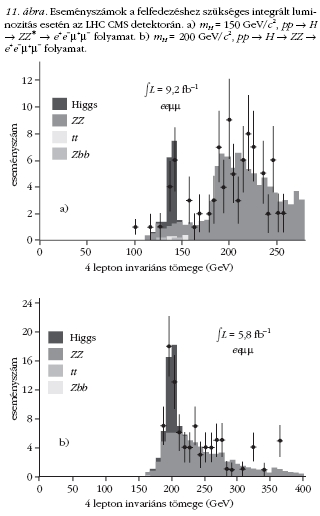
Kisebb Higgs-tömeg esetén
ugyanebben a csatornában csak az egyik Z bozon
valódi, a másik virtuális. A részletes tanulmányok szerint
a 130 GeV/c² ≤ mH ≤ 160 GeV/c² ablakban ez a
csatorna szintén biztos felfedezéshez vezet. A 11.
ábra tanúsága szerint négy töltött lepton invariáns
tömegének eloszlásában a Higgs-rezonancia a háttérből
jól kiemelkedik már viszonylag kevés integrált
luminozitás esetén is. A 160 GeV/c² ≤ mH ≤ 180
GeV/c² ablakban a pp → H → W+ W- → 2l 2v
csatorna siet segítségünkre. A CMS tanulmánya szerint (12.
ábra ) mH ≈ 165 GeV/c² tömeg esetén már 1 fb-1 integrált
luminozitás elegendő a felfedezéshez!
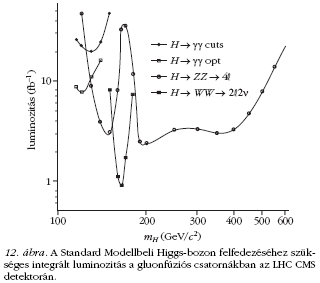
A 12. ábráról kitűnik, hogy a gluonfúzióban keletkező
Higgs-bozon az LHC rövid működése során is
nagy biztonsággal észrevehető a végállapoti részecskék
invariáns tömegeloszlásában. Mégis lényeges és
érdekes más csatornák felderítése is. Az egyes csatornákban
kapott eredmények összehasonlításával ellenőrizhetjük
eredményeinket. Továbbá a felfedezés
csak az első lépés. Fontos és sokkal nehezebb feladat
a felfedezett részecske tulajdonságainak meghatározása,
amihez minél több adatra van szükség.
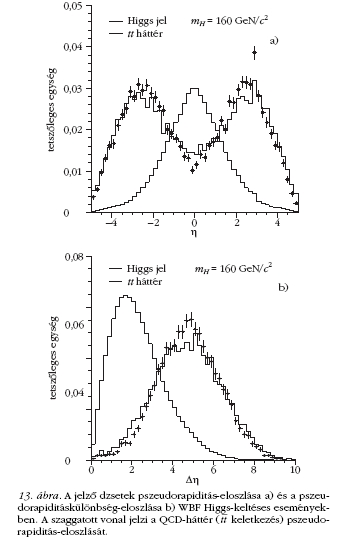
Tanulságos
például felderíteni az 5.b ábrán mutatott WBF
Higgs-keletkezés kimutatásának lehetőségét is. Bár a
keltési ráta mintegy tizede a gluon-gluon fúzióban
való keletkezésnek, a végállapot különleges kinematikai
szerkezete lehetővé teszi a háttér elnyomását.
A végállapotban megjelenő kvarkok előre-hátra
szóródnak és a detektor véglezáróiban hadronzáporként
jelennek meg (ezeket hívják jelző dzseteknek ).
A Higgs-részecske bomlástermékei ellenben főként a
detektor oldalai (hordó) irányába távoznak. Az azonos
végállapotú, de Higgs nélküli háttéresemények
hadronikus aktivitása sokkal inkább a hordó felé
irányul, ezért a dzsetek pszeudorapiditása [η =
-ln tan(θ / 2), θ a dzset lendületvektora és a nyalábtengely
által bezárt szög] szerinti vágással a háttér elnyomható
(13. ábra).
Összefoglalásként azt mondhatjuk, hogy a Standard
Modell Higgs-bozonja biztonsággal felfedezhető
az LHC-nál, ha tömege nagyobb a LEP kizárási határnál,
de kisebb 600-700 GeV/c²-nél. Az olvasóban joggal
merül fel a kérdés, mi van, ha mH ≥ 700 GeV/c².
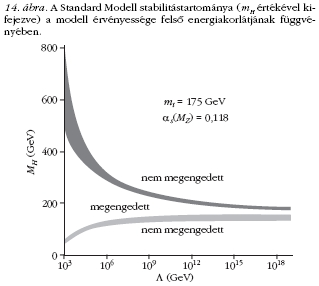
Itt nem részletezendő elméleti megfontolásokból
kiderül, hogy a Standard Modell csak akkor ellentmondásmentes
elmélet valamely λ energiáig, ha a
Higgs-bozon tömege λ-tól függő jól meghatározott
tartományba esik (14. ábra). Ha tehát az LHC detektorai
nem mutatnak a Standard Modell Higgs-bozonjára
utaló jelet, akkor mindenképpen új fizikát kell
találni az LHC-nál. Véleményem szerint valószínűbb,
hogy a kísérletek találnak majd valamit, ami a Higgs-rezonanciára
hasonlít. Hogy megtudjuk, mit is sikerült
valójában felfedezni, meg kell mérni a
rezonancia elektromos és színtöltését [mindkettő semleges],
tömegét [mérendő szabad paraméter], spinjét [0], CP
kvantumszámát [páros], csatolását a mértékbozonokhoz
[SU(2)L jelleg] és a fermionokhoz [mf /v ], önkölcsönhatásait
(a Higgs-potenciált) [mH rögzíti] - szögletes
zárójelben a Standard Modell-beli Higgs-bozon
jellemzőit találjuk. Az írás elején vázolt Standard Modell
kísérleti bizonyításához a lista legutolsó és egyben
legnehezebben kivitelezhető eleme elengedhetetlen.
_____________________________
Elhangzott 2007. augusztus 24-én az ELFT Fizikus Vándorgyűlésén.
_____________________________
1 Egyes szerzők a családok 16.tagjaként a jobbkezes neutrínókat
is beszámítják.Minthogy a Standard Modellben azok egyik részecskével
sem hatnak kölcsön, ezért kísérleti kimutatásuk részecskeütközésekben
nem lehetséges.
2 A bennünket felépítő anyag tömegét nagyrészt az atommagokban
található protonok és neutronok egyesített tömege adja, amelyek
pedig tömegük jelentős részét az azokat felépítő kvarkok és
gluonok kötésének köszönhetik.

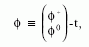
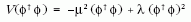
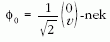
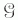 generátorhoz
(Pauli-mátrixok, illetve a 2 × 2-es egységmátrix) tartozó
U =
generátorhoz
(Pauli-mátrixok, illetve a 2 × 2-es egységmátrix) tartozó
U = 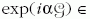 G transzformációval szemben, ha
UΦ0 = Φ0, ahonnan
G transzformációval szemben, ha
UΦ0 = Φ0, ahonnan 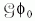 = 0
következik. Gyors számítás
mutatja, hogy ez egyik csoportgenerátorral sem
teljesül, de az elektromos töltésre igen, tehát a vákuum
az eredeti SU(3)c × SU(2)L × U(1)Y szimmetriát
SU(3)c × U(1)EM szimmetriára sérti.
Természetesen a skalárteret tartalmazó elméletnek
is G-invariánsnak kell lennie, amelynek következményeként
a kölcsönhatást közvetítő mértékbozonok a
fermionokon kívül a skalártérrel is kölcsönhatnak. A
szimmetriasérülés eredményeként a skalártér alapállapotával,
a vákuummal való kölcsönhatás a gyenge
mértékbozonoknak a v vákuum várhatóértékkel arányos
tömeget ad. A Φ0 alapállapot körül
= 0
következik. Gyors számítás
mutatja, hogy ez egyik csoportgenerátorral sem
teljesül, de az elektromos töltésre igen, tehát a vákuum
az eredeti SU(3)c × SU(2)L × U(1)Y szimmetriát
SU(3)c × U(1)EM szimmetriára sérti.
Természetesen a skalárteret tartalmazó elméletnek
is G-invariánsnak kell lennie, amelynek következményeként
a kölcsönhatást közvetítő mértékbozonok a
fermionokon kívül a skalártérrel is kölcsönhatnak. A
szimmetriasérülés eredményeként a skalártér alapállapotával,
a vákuummal való kölcsönhatás a gyenge
mértékbozonoknak a v vákuum várhatóértékkel arányos
tömeget ad. A Φ0 alapállapot körül
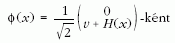
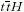 együttes keltés.
A 6. ábra mutatja a Tevatron- és LHC-energiákon
számolt keltési hatáskeresztmetszeteket a Higgstömeg
függvényében. Az LHC-n a 100 GeV-es energiatartományba
eső részecskék keltésében a gluonütközések
fognak lényeges szerepet játszani, így a
Higgs-keltés fő folyamata a gluonfúzió.
A Higgs-bozon a Standard Modell többi részecskéjénél
nehezebb (a LEP kizárási határ szerint csak a top
kvark lehet nehezebb nála) ezért a keletkezett Higgs
rögtön el is bomlik elsősorban nehéz részecskék párjaiba.
A Higgs tömegétől függ, hogy melyek a lényeges
bomlási csatornák, hiszen nemcsak a csatolás
erőssége, hanem a kinematikai küszöb is lényegesen
befolyásolja részecskepár keletkezésének valószínűségét.
A 7. ábra mutatja a Higgs-bozon elágazási arányait
(a parciális bomlási szélesség aránya a teljes
bomlási szélességhez, Γi /Γtot) tömegének
függvényében. Látjuk, hogy a kis tömegek tartományától
eltekintve - ahol a
együttes keltés.
A 6. ábra mutatja a Tevatron- és LHC-energiákon
számolt keltési hatáskeresztmetszeteket a Higgstömeg
függvényében. Az LHC-n a 100 GeV-es energiatartományba
eső részecskék keltésében a gluonütközések
fognak lényeges szerepet játszani, így a
Higgs-keltés fő folyamata a gluonfúzió.
A Higgs-bozon a Standard Modell többi részecskéjénél
nehezebb (a LEP kizárási határ szerint csak a top
kvark lehet nehezebb nála) ezért a keletkezett Higgs
rögtön el is bomlik elsősorban nehéz részecskék párjaiba.
A Higgs tömegétől függ, hogy melyek a lényeges
bomlási csatornák, hiszen nemcsak a csatolás
erőssége, hanem a kinematikai küszöb is lényegesen
befolyásolja részecskepár keletkezésének valószínűségét.
A 7. ábra mutatja a Higgs-bozon elágazási arányait
(a parciális bomlási szélesség aránya a teljes
bomlási szélességhez, Γi /Γtot) tömegének
függvényében. Látjuk, hogy a kis tömegek tartományától
eltekintve - ahol a 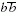 párba való bomlás a legvalószínűbb
-, a gyenge vektorbozonok uralják a Higgsbomlás
végállapotát. Vegyük észre, hogy kis valószínűséggel
ugyan, de nulla tömegű részecskék is lehetnek
a végállapotban: gg, Zγ, valamint γγ,, aminek a
továbbiakban lényeges szerepe lesz. A fontos következtetés
az, hogy a Higgs-részecske a tömegétől függően
más-más részecskékbe szeret elbomlani.Ebből
következik, hogy a felfedezéshez vezető keresési csatornák
is függenek a Higgs-tömegtől.
A Higgs-bozon nehéz a többi részecskéhez képest,
ezért az ütközési kísérletekben viszonylag ritkán keletkezik.
Más végállapotok valószínűsége sokkal nagyobb.
A 8. ábrán a proton-(anti)proton ütközésekben megjelenő
végállapotok hatáskeresztmetszetét látjuk a tömegközépponti
energia függvényében. Alacsonyabb energiákon
párba való bomlás a legvalószínűbb
-, a gyenge vektorbozonok uralják a Higgsbomlás
végállapotát. Vegyük észre, hogy kis valószínűséggel
ugyan, de nulla tömegű részecskék is lehetnek
a végállapotban: gg, Zγ, valamint γγ,, aminek a
továbbiakban lényeges szerepe lesz. A fontos következtetés
az, hogy a Higgs-részecske a tömegétől függően
más-más részecskékbe szeret elbomlani.Ebből
következik, hogy a felfedezéshez vezető keresési csatornák
is függenek a Higgs-tömegtől.
A Higgs-bozon nehéz a többi részecskéhez képest,
ezért az ütközési kísérletekben viszonylag ritkán keletkezik.
Más végállapotok valószínűsége sokkal nagyobb.
A 8. ábrán a proton-(anti)proton ütközésekben megjelenő
végállapotok hatáskeresztmetszetét látjuk a tömegközépponti
energia függvényében. Alacsonyabb energiákon
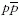 (Tevatron), magasabb energiákon pp (LHC)
ütközések hatáskeresztmetszetei láthatók (a 4 TeV-nél
látható szakadás mutatja a váltást). Azt látjuk, hogy a
Higgs-bozon keletkezésének valószínűsége nagyságrendekkel
kisebb más Standard Modell-beli folyamatok valószínűségénél.
A Higgs bomlástermékei ugyanazok a
részecskék, amelyek ezekben a más folyamatokban is
keletkeznek, ezért a Higgs-keletkezésre utaló jelet mindig
nagy háttér felett kell megtalálni.
A Higgs-keresés esetén a jel (S ) és háttér (B) viszonya
kétféle lehet: (i) a Higgs-bomlás eredményeként
keletkező részecskepár invariáns tömegeloszlásában
a Higgs-keletkezéshez tartozó rezonancia egy sima
háttéren ül, (ii) a Higgs-keletkezés jele és a háttér
alakja hasonló. Az első esetben a keresés tisztán kísérleti
úton sikeres lehet. A háttér jól meghatározható
a rezonancia két oldalán található eloszlásból, annak
levonásával a rezonanciacsúcs egyértelművé válik. A
siker feltétele, hogy a jel szignifikanciája, ami nagyjából
az S · B1/2 viszony, elegendően nagy legyen. Az
ötnél nagyobb érték a biztos felfedezés (99,999%-os
biztonságú) elfogadott szintje.
Tekintsük először a kis Higgs-tömegek tartományát!
Legkézenfekvőbbnek tűnhet a jel leggyakoribb
végállapotát (H →
(Tevatron), magasabb energiákon pp (LHC)
ütközések hatáskeresztmetszetei láthatók (a 4 TeV-nél
látható szakadás mutatja a váltást). Azt látjuk, hogy a
Higgs-bozon keletkezésének valószínűsége nagyságrendekkel
kisebb más Standard Modell-beli folyamatok valószínűségénél.
A Higgs bomlástermékei ugyanazok a
részecskék, amelyek ezekben a más folyamatokban is
keletkeznek, ezért a Higgs-keletkezésre utaló jelet mindig
nagy háttér felett kell megtalálni.
A Higgs-keresés esetén a jel (S ) és háttér (B) viszonya
kétféle lehet: (i) a Higgs-bomlás eredményeként
keletkező részecskepár invariáns tömegeloszlásában
a Higgs-keletkezéshez tartozó rezonancia egy sima
háttéren ül, (ii) a Higgs-keletkezés jele és a háttér
alakja hasonló. Az első esetben a keresés tisztán kísérleti
úton sikeres lehet. A háttér jól meghatározható
a rezonancia két oldalán található eloszlásból, annak
levonásával a rezonanciacsúcs egyértelművé válik. A
siker feltétele, hogy a jel szignifikanciája, ami nagyjából
az S · B1/2 viszony, elegendően nagy legyen. Az
ötnél nagyobb érték a biztos felfedezés (99,999%-os
biztonságú) elfogadott szintje.
Tekintsük először a kis Higgs-tömegek tartományát!
Legkézenfekvőbbnek tűnhet a jel leggyakoribb
végállapotát (H → 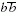 )
választani keresési csatornaként,
azonban ez esetben a jel elvész a hatalmas háttérben.
Minthogy hadronütköztetőn a hadronikus
végállapotok óriási túlsúlyban vannak, ezért az általános
ökölszabály szerint olyan végállapotokra érdemes
figyelni, amelyekben legalább egy nagy energiájú
lepton van a végállapotban. Ilyen esetekben a háttér
lényegesen kisebb, vagy megfelelő vágásokkal kisebbé
tehető. Az egyes keresési csatornák részletes vizsgálata
azt mutatja, hogy 30 fb-1 integrált luminozitás3
esetén a következő csatornák egyesített eredményei a
Standard Modell-beli Higgs-bozonnak a CMS detektoron
való biztos felfedezéséhez vezet az mH = 100-600
GeV/c2 tömegtartományban:
)
választani keresési csatornaként,
azonban ez esetben a jel elvész a hatalmas háttérben.
Minthogy hadronütköztetőn a hadronikus
végállapotok óriási túlsúlyban vannak, ezért az általános
ökölszabály szerint olyan végállapotokra érdemes
figyelni, amelyekben legalább egy nagy energiájú
lepton van a végállapotban. Ilyen esetekben a háttér
lényegesen kisebb, vagy megfelelő vágásokkal kisebbé
tehető. Az egyes keresési csatornák részletes vizsgálata
azt mutatja, hogy 30 fb-1 integrált luminozitás3
esetén a következő csatornák egyesített eredményei a
Standard Modell-beli Higgs-bozonnak a CMS detektoron
való biztos felfedezéséhez vezet az mH = 100-600
GeV/c2 tömegtartományban: