Fizikai Szemle honlap |
Tartalomjegyzék |
Simon Péter
Leőwey Klára Gimnázium, Pécs
Erdős Pál (1913-1996), a világhírű magyar matematikus a nyolcvanadik születésnapján adott tévéinterjúban közölte, hogy ő maga 2,5 milliárd éves. E meglepő kijelentés bizonyítása igen röviden a következő: "Amikor kicsi voltam, akkor a Föld 2 milliárd éves volt. Most [1993-ban] 4,5 milliárd éves." Ez a szokatlan érvelés adta az ötletet, hogy áttekintsem, az egyes korokban mit is gondoltak a Föld koráról.
A zsidó-keresztény kultúrkörben a világ teremtett, amelyből óhatatlanul következik, hogy bolygónknak története és életkora is van. Az európai gondolkodásban sok mindenhez a Biblia adja a sorvezetőt. Leginkább olyan kérdésekben, amelyekre a tudomány sokáig nem tudott egzakt, minden gondolkodó által elfogadható választ adni. Leonardo da Vinci a tengerparttól több mint 200 km-re tengeri halak kövületeit találta. A 15. században korrekt válasznak tűnt, hogy a halak az özönvíz idején kerültek ilyen messzire a tengerparttól. Ezt a magyarázatot széles körben elfogadták, annak ellenére, hogy Alhazan, az arab orvostudós már a 11. században azt feltételezte, hogy a halak kövületei a tengerek alján a kőzetek kialakulásakor keletkeztek, s a földmozgások juttatták őket a vizektől távol a szárazföld belsejébe. Hasonló feltételezést a nyugati tudományban csak Nicolaus Steno fogalmazott meg a 17. század második felében. Steno, egy dán orvos dolgozta ki a rétegtan alapjait.
A Biblia megkérdőjelezhetetlen tekintélyének köszönhetően a Föld korát először a Biblia alapján próbálták megállapítani. James Ussher ír érsek az Írásban előforduló generációkat vette sorra, s az első emberpár megjelenésének idejét i. e. 4000-re teszi. Volt nála merészebb ember is. John Lightfoot, a cambridge-i egyetem teológia-professzora 1654-ben kijelentette, hogy a teremtés i. e. 4004. október 26-án délelőtt 9 órakor történt. A pontos időponthoz hibahatárt sem adott meg. A földtudomány ezen az adaton természetesen már rég túllépett. Ennek a becslésnek viszont kultúrtörténeti jelentősége van, a Biblia által leírt történet hosszát adja meg.
Sir Charles Lyell (jogász, 1797-1875) a kontinensen tett utazásai során figyelte meg a földtani formák változatosságát. 1830 és 1833 között írt egy háromkötetes munkát A geológia elvei címmel, ami alapműnek tekinthető a geológiában. Ebben a műben kijelenti, hogy az ismertté vált kövületek alapján nem kizárt, hogy a Föld kora meghaladja a százmillió évet is. Ezen a kijelentésen az egyház természetesen megbotránkozott.
Charles Darwin ismerte Lyell elképzelését a Föld korára vonatkozóan. A Beagle fedélzetén gyakran olvasgatta ezt a művet is. Örült ennek a jóslatnak, hisz a Fajok eredete (1859) című híres könyvében felvázolt evolúciós elmélet azt feltételezi, hogy az élővilág fejlődéséhez igen hosszú időre volt szükség. Két tudományág - a geológia és a biológia - egyetértett a Föld korát illetően. Korrekt bizonyítás nélkül azt mondták, hogy a Föld több mint 100 millió éves. És beleszóltak a vitákba a fizikusok.
Először a termodinamika felől közelítettek a kérdéshez a fizikusok. Isaac Newton az 1687-ben megjelent Principiában adott egy becslést, amely szerint a Föld izzó állapotából körülbelül 50 ezer év alatt hűlhetett le. Newton főműve a mechanika alaptörvényeiről, a mozgást leíró törvényekről vált ismertté. A Földre alkalmazott termodinamikai modell kevés figyelmet kapott.
Buffon gróf (George-Louis Leclerc, 1707-1788) a problémán való gondolkodáson túl már kísérletet is végzett. Párizs mellett nagy átmérőjű agyag-, illetve vasgömböket hevített, s azok hűlését tanulmányozta. Ezen vizsgálatok után jelentette ki, hogy a Föld kora 75 ezer év.
A Föld kora nyilván kapcsolódik a Naphoz. A Napot a 19. század elején égő széngömbnek vélték, amely sugárzása révén veszíti el energiáját. A napsugárzás teljesítménysűrűsége a Földön 1400 W/m2 (napállandó). Tételezzük fel, hogy ez az intenzitás a jövőben sem csökken. A Nap tömege 2 · 1030 kg, távolsága a Földtől 1,5 · 1011 m, a szén fűtőértéke 30 MJ/kg. Mennyi ideig sütne még a Nap, ha valóban égő szénből állna? Ezzel a kérdéssel 200 éve még komoly tudósok foglalkoztak, ma már egy ügyes középiskolásnak is megoldható feladat. (KöMaL 2002/03, P. 3518.)
Az égő széngömb hipotézise szerint a Nap rendelkezésre álló teljes energiája:
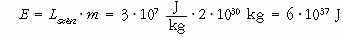
lenne. A napsugárzás intenzitását a Nap-Föld távolsággal egyenlő sugarú gömb felszínével megszorozva megkapjuk a jelenlegi (T0 = 6000 K hőmérsékletű) Nap teljes sugárzási teljesítményveszteségét:
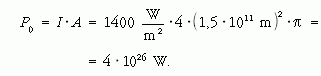
A teljes energia kisugárzásához szükséges idő:
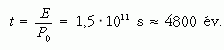
Ha elhanyagoljuk a már kiégett, de még forró (izzásban lévő) parázs kihűléséhez szükséges időt, akkor csupán ilyen rövid ideig, nem egészen ötezer évig "sütne" a Nap.
Ehhez közeli szám szerepel Madách drámájában, Az ember tragédiája (1860) 13. színében (Lucifer):
A Napot egy 6000 K hőmérsékletű, homogén izzó gázgömbnek is tekinthetjük, amely H2 molekulákból áll és a hősugárzás során lassan hűl. Most ismét felhasználjuk, hogy a napsugárzás intenzitása a Földünk távolságában jelenleg 1400 W/m2. Becsüljük meg, mennyi idő múlva sötétülne el a Nap, vagyis csökkenne a hőmérséklete körülbelül 1000 K-re? (KöMaL 2002/04, P. 3529.)
A Nap sugárzásának jelenlegi teljesítménye ismét:
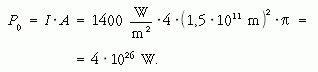
Ha az m tömegű Napot T hőmérsékletű hidrogéngáznak tekintjük, és belső energiáját az ideális gázokra érvényes E = cV · m · T képletből számítjuk, valamint a fajhőt a földi hőmérsékleten érvényes cV = 104 J/kg · K értékkel közelítjük:
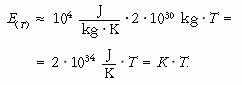
Ha a sugárzás erőssége nem csökkenne, akkor a ΔT = 5000 K hőmérséklet-változáshoz szükséges idő a P · Δt = K · ΔT alapján:
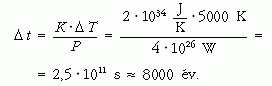
Ez a meglepően kicsiny érték a meglehetősen durva közelítésnek köszönhető. Vegyük figyelembe a teljesítmény hőmérsékletfüggését!
Amennyiben a Nap hőmérséklete csökken, akkor a Stefan-Boltzmann sugárzási törvénynek megfelelően csökken a teljesítménye is:
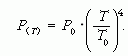
A hűlés időtartamának meghatározásához integrálszámítást kell használnunk:
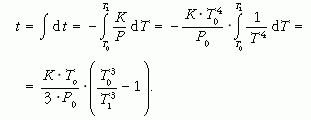
A t értéke T1 = 1000 K-nél körülbelül 700 000 év.
Ez azt jelenti, hogy ha a Nap az izzó gázgömb energiáját sugározná ki, akkor még 700 ezer évig sütne.
A T1 → ∞ határérték képzésével azt az időtartamot is megkaphatjuk, ami alatt a tetszőleges nagy hőmérsékletű Nap a jelenlegi T0 = 6000 K hőmérsékletűre hűl. A megdöbbentő
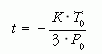
érték kevesebb, mint 4 ezer év. Tehát ezen modell szerint a Nap kora kevesebb mint 4 ezer év. Ez alapján az ószövetségi történet közben keletkezett volna a Napunk. Ez nyilván ellentmond a tapasztalatnak.
Lord Kelvin (William Thomson, 1824-1907) a 19. század nagy brit fizikusa más oldalról közelítette meg ezt a kérdést. Szerinte a Nap által kibocsátott energia a gravitációs összehúzódásból ered. A csillag teljes energiája megegyezik az őt alkotó részecskék Ebelső kinetikus energiájának összegével, valamint a részecskék Epot gravitációs potenciális energiáinak összegével: E = Ebelső + Epot. A viriál-tétel értelmében egy zárt rendszer kinetikus energiája a gravitációs potenciális energia nagyságának felével egyenlő. Vegyük figyelembe még azt is, hogy a Napot alkotó gáz adiabatikus állapotváltozást szenved. Így a teljes energiájára a következő adódik:
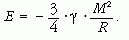
Amennyiben a gázgömb összehúzódik, a teljes energiája csökken. A Nap teljes energiájának a megváltozása biztosítja a Nap energiatermelését:
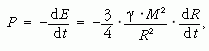
ahonnan
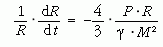
következik. A Nap adatait behelyettesítve:
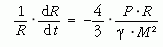
A fenti egyenletet átrendezve, valamint a Nap teljes sugarára integrálva megkapjuk azt az időtartamot, amennyi alatt a Nap elsötétül:
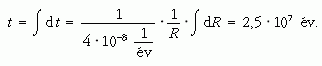
Tehát, ha a Nap a gravitációs összehúzódásból nyerné energiáját, akkor a jelenlegi sugárzás mellett 25 millió év alatt sötétülne el. Lord Kelvinnek és a fizika egzaktságának olyan nagy tekintélye volt, hogy 1860- ban Darwin visszavonta a Fajok eredetében írt feltételezést, hisz szerinte a földi élet evolúciójához több mint 100 millió évre volt szükség.
Thomas C. Chamberlin (amerikai geológus, 1843- 1928) 1899-ben fogalmazta meg: "Ha a fizika a Föld korára ilyen rövid időt ad meg, akkor a fizikának nincs igaza."
Tételezzük fel, hogy a Föld keletkezésekor a 238U és a 235U izotópok jelen voltak, bomlástermékeik viszont hiányoztak. A 238U és a 235U bomlását használjuk fel a Föld T életkorának meghatározásához.
A 238U izotóp felezési ideje 4,5 · 109 év. A bomlástermékek felezési ideje ehhez képest olyan rövidnek tekinthető, hogy létezésüket első közelítésben elhanyagolhatjuk. A bomlási sorozat a stabil 206Pb izotópban végződik. A 235U izotóp 0,71 · 109 év felezési idővel rövid felezési idejű bomlástermékeken keresztül stabil 207Pb izotópot eredményez.
A Föld korának jelenlegi legjobb közelítését a Patterson-féle (1956) meteoritmódszer szolgáltatja. Patterson azt feltételezi, hogy a meteoritok a Földdel azonos ősanyagból egyidejűleg képződtek, majd a képződés után elszakadtak. Ezen meteoritok jelenlegi ólomizotóp összetétele nyilvánvalóan két tényezőtől függ: egyrészt a keletkezésük pillanatában már meglévő ősólom-összetételüktől, másrészt a keletkezésük pillanatában meglévő U és Th mennyiségétől, hisz ezek is ólomizotópokat termelnek. Válasszunk ki olyan meteoritot, amelyben nincs, vagy elhanyagolhatóan kevés az U és a Th. Ez a meteorit az ősólom-izotóp összetételét őrzi.
Uránércet tömegspektrométerrel vizsgáltak. A 204Pb, 206Pb és 207Pb izotóp relatív koncentrációjának mérése az adott atomok számának következő arányát eredményezte: 1,00 : 29,6 : 22,6. A 204Pb izotópot használtuk referenciaként, mivel ez az izotóp nem radioaktív eredetű. Az uránmentes meteorit (tiszta ólomérc) vizsgálata a következő arányokat eredményezte: 1,00 : 17,9 : 15,5.
A bomlási törvény szerint a kezdetben N0 darab U izotópból t idő múlva keletkező 206Pb száma:
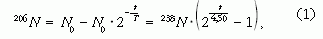
ahol 238N a jelenlegi U izotópok számát jelöli. Az előzőekhez hasonlóan 235U izotópból t idő múlva keletkező 207Pb száma:
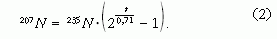
Az urán-ólom keverékben (ahol a radioaktív bomlások során folyamatosan keletkeznek ólomatomok), a különböző tömegszámú ólomizotópok számának aránya:
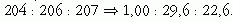
A tiszta ólomban a megfelelő arányok:
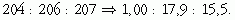
A fenti arányszámok különbségét képezve látható, hogy a radioaktív bomlásokból származó ólomizotópok aránya:
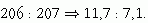
Az (1) és (2) egyenlőségek hányadosát képezve:
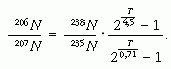
Helyettesítsük be a radioaktív bomlásokból származó ólomizotópok arányát, valamint a 238N : 235N jelenlegi 137 : 1 értékét!
A Föld T életkorára a következő egyenletet kapjuk:
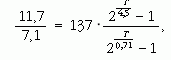
Vagyis
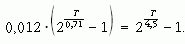
Feltételezve, hogy T >> 4,5 · 109 év, a fenti formulában a zárójelekben az 1-eseket elhanyagolhatjuk, s T-t milliárd években könnyen kifejezhetjük:
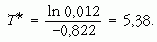
Láthatjuk, hogy ez a közelítő érték nem sokkal nagyobb, mint a hosszabb felezési idő. Tehát a kiszámítása során alkalmazott elhanyagolás nem volt jogos! Viszont felhasználható egy pontosabb T érték meghatározására. Jelöljük a Föld életkorára durva közelítésben kapott 5,38 milliárd évet T*-gal, s az eredeti egyenlet helyett tekintsük a
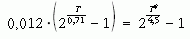
egyenletet. Ez zárt alakban megoldható, így T-re 4,80 · 109 év adódik. Ha ezen értéket írjuk T* helyébe, T-re még jobb közelítést, 4,62 · 109 évet kapunk. Ezt a (fokozatosan közelítő) eljárást tovább folytatva az eredmények 4,52 · 109 évhez konvergálnak.
Ezt a sok, kényelmetlen számolást szívesen elvégzi helyettünk a számítógép. A Mathematica program segítségével pillanatok alatt megkapjuk a fenti exponenciális egyenlet megoldását például 5 tizedesjegy pontossággal.
Megadjuk az egyenlet megoldására vonatkozó utasítást ...
FindRoot[0.012 (-1+2^(T/0.71))=-1+2^(T/4.5),{T,5}]
... és pillanatok alatt megkapjuk az eredményt:
{T=4.56178}.
A grafikus megoldással (Excel) is kaphatunk egy közelítő
megoldást (1. ábra).
(Az imént tárgyalt probléma a XXXI. Fizikai Diákolimpia [Leicester, 2000] egyik feladataként szerepelt.)
<>
A Föld koráról vallott elképzelések igen érdekesen változtak az elmúlt szűk 400 évben. A naivitás és a feltétlen tekintélytisztelet szülte a bibliai alig 6000 éves kort. A geológia és a biológia igényelt volna 100 millió évet, csak igazolni nem tudta. A radioaktivitás ismerete adott lehetőséget a ma helyesnek gondolt 4,5 milliárd éves életkor meghatározására.
Irodalom
______________
1 A pécsi Leőwey Klára Gimnáziumban 2008. november 6-án, a Magyar Tudomány Napján tartott előadás írott változata