KINEMATIKA A KARTEZIÁNUS FIZIKÁBAN
Az elmozdulás, az idő és a sebesség értelmezése

Kistüttősi Gyula,
BME Filozófia és Tudománytörténeti Tanszék

Írásomban a mechanikus filozófia¹ mozgással kapcsolatos fogalmait, változóit és egyenleteit szeretném megvizsgálni. Descartes a mozgással kapcsolatos elméletét kidolgozta ugyan, de talán nem egyértelműen fogalmazta meg, vagy ami még valószínűbb, a newtoni mechanika térhódítása miatti szemléletváltás, az alapvető ontológiai entitások megváltozása, értelmetlenné, félreérthetővé tették. Úgy vélem, a newtoni paradigmában értelmezett sebesség, idő, út, lendület fogalma alkalmatlan a karteziánus fizika értelmezésére, ezért célom, hogy a Filozófia alapelvei [7] vonatkozó pontjait elemezve ezeknek a látszólag triviális, de valójában erősen a klasszikus mechanika által befolyásolt fogalmaknak egy új értelmezését adjam, oly módon, hogy felhasználásukkal a karteziánus fizika konzisztens elméletként legyen interpretálható.

Így nem használom fel kritikátlanul a newtoni eredetű meghatározásokat, hanem olyan definíciók megadására törekszem, amelyek illeszkednek a descartes-i szövegekhez, ugyanakkor egymással is összefüggő, egységes elméletet alkotnak, olyat, amely Descartes szemében alkalmasnak tűnhetett a jelenségek magyarázatára.

A tudományos tudás történetének mai felfogása révén előtérbe került az elfeledett, elbukott, meghaladott tudományos elméletek vizsgálata, belső összefüggéseik megértése. Ebből a szempontból Descartes munkássága mindenképpen kiemelt figyelemre tarthat számot. Kora egyik legnagyobb hatású természettudósa volt, még akkor is, ha a későbbiekben háttérbe szorult, és elmélete jelentős részét elvetették. De mint Kvasz László [2] kimutatta, fizikája jelentős hatást gyakorolt a newtoni tudományra, és a modern tudományos eljárás módszertanát az ő munkássága alapozta meg. Ezért is érdekes, hogy természettudományára szinte sehol sem találunk hivatkozásokat. Kuhn alapján azt mondhatjuk, hogy mint vesztes paradigmát, teljesen törölték a tudományos szakirodalomból.

Kritikák összefoglalása

A karteziánus fizikával szemben napjainkig számos kritikát fogalmaztak meg. A következőkben szeretném összefoglalni a legfontosabbakat azok közül, amelyek érintik a sebesség fogalmát.

1. kritika

A descartes-i fizikát tárgyaló írások egy részében a sebesség fogalmát nem elemzik, és feltétel nélkül elfogadják napjaink hétköznapi, vagy a newtoni fizika szerinti értelmezését [3], vagy vizsgálják ugyan, de átlagsebességről, vagy nagyon rövid idő alatti (pillanatnyi) sebességről beszélnek [4]. Senki sem elemzi, hogy mit is jelent a sebességet meghatározó két tényező, az elmozdulás és az idő. Ez utóbbi Descartesnál csupán a dolgok szemléletmódja, míg az előbbi jelentése kiterjedt testek esetén nem tisztázott. Jóllehet emiatt a sebesség fogalma nem tekinthető egyértelműen meghatározottnak, minden további elemzés nélkül fogalmaznak meg kritikát a descartes-i fizika inkonzisztenciáját illetően [5].

2. kritika

Descartes nem fejtette ki teljes körűen a mozgásmennyiséget befolyásoló tényezőket, mert bár említi a felületet és a környezetet (közegellenállást) is, a mozgástörvényekben a későbbiekben már csak a sebességet és a kiterjedést veszi figyelembe [6]. Így a karteziánus fizika kidolgozatlan, sőt zavaros.

3. kritika

Descartes matematikai (mennyiségi) fizikáról beszél, de valójában minőségit csinál, nincsenek konkrétmennyiségi viszonyok. Miközben deklarált célja a fizika matematizálása, valójában nincs egyetlen olyan tétele sem, amelyikben kvantitatív változók szerepelnének. Ezért fizikája inkább az arisztotelészi fizika csúcspontja, mint a modern természettudomány kezdete.

Az elmozdulás

Ahogy napjaink hétköznapi gondolkodása a klasszikus fizika tér-idő felfogására épül, úgy határozták meg a skolasztikus fogalmak és szemléletmód a 17. század fizikai gondolkodását. S ahogy nekünk kényszeríteni kell magunkat, hogy egy másik fogalomrendszerbe tudjunk helyezkedni, úgy kellett a kor gondolkodóinak erőfeszítéseket tenniük, hogy új szemléletmódot vezethessenek be. Ezeknek a szemléletmódoknak némelyike lehet, hogy zsákutcának bizonyult, vagy már a kidolgozásakor hibás volt, de volt olyan is, amelyik pusztán feledésbe merült. Így könnyen lehet, hogy később hibásnak, hiányosnak bélyegezték, pusztán azért, mert nem értették meg. Ezért nem értelmezhetjük a karteziánus kinematikát a klasszikus felfogásban, hanem rekonstruálni kell az elmozdulás, az idő és a sebesség descartes-i felfogását.

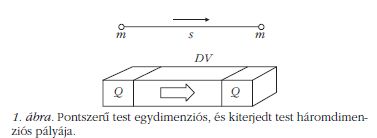
Ha a testeket² egy adott vonatkoztatási rendszerben 1. ábra.  vizsgáljuk, és megállapítjuk, hogy közülük némelyik mozog, akkor meg kell tudni határozni az elmozdulásukat. Mindenekelőtt azonban tisztázni kell a lehetséges mozgás jellegét. Descartes elutasította az okkult entitások, így a távolhatás (erő) feltételezését. Hatást a testek kizárólag közvetlen érintkezés révén képesek egymásra kifejteni, gyakorlatilag ütközések révén. Az a priori kifejtett első természeti törvény kimondja, hogy a magára hagyott test mozgását egyenletesen, míg a második, hogy egyenes vonalban folytatja [7] mindaddig, amíg valamely más testtel ütközve sebességének nagysága vagy iránya megváltozik. A gyorsító erő létének elutasítása miatt a karteziánus fizikában nem értelmezhető a gyorsulás sem, legfeljebb a sebesség ütközések sorozata által kiváltott, diszkrét ugrásokkal való változásáról beszélhetünk. A továbbiakban tehát kizárólag egyenes vonalú, egyenletes mozgásról lesz szó.

A két tetszőleges állapot közt megtett út meghatározása során problémát okoz, hogy miként lehet egy test mozgását leírni. Ez lehetséges egy vonallal, mint pályával, egy pont, vagy pontszerű test esetén (mint amilyen a newtoni tömegpont), de semmiképpen sem a descartes-i fizika által feltételezett kiterjedt testek esetében. Ezek a testek nem egy vonalszerű utat járnak be, hanem, mivel van a mozgásra merőleges felületük, sokkal inkább egy tértartományt. Akkor járunk el helyesen, ha a megtett út helyére a bejárt térrészt képzeljük, mert így megkapjuk a descartes-i értelemben vett elmozdulást (1. ábra). Descartes a következőket mondja: „A filozófusok több mozgást is feltételeznek .... Én viszont csak egyet ismerek, azt, amely könnyebben ismerhető meg, mint a geométerek vonalai: mely oka annak, hogy a testek az egyik helyről a másikra haladnak, és egymás után foglalják el az összes teret a kettő között.” [8]

Adjuk meg a karteziánus fizikai mennyiségeket és a köztük fennálló viszonyt úgy, hogy a definíciók illeszkedjenek a descartes-i szöveghelyekhez. Mindenekelőtt különítsük el a test Q kiterjedését az általa elfoglalt tér V kiterjedésétől. Legyen az elfoglalt tér a mozgás kezdetén V₁, a végén V₂, a mozgás során a test által bejárt térrészt jelölje DV (2. ábra).

Q = V₁ = V₂ ,

V₁ + DV = DV + V₂

Nyugvó test esetén V₁ ≡ V₂, mivel DV = 0.

A Q és a DV jellege közti különbség, hogy DV a térhez, míg Q a testhez tartozik, de mindkettő kiterjedés, azaz hossz, szélesség és mélység által meghatározott. Legyen s a test egyenes vonalú elmozdulása a mozgás irányában, és A a kiterjedt testnek a mozgás irányára merőleges síkra eső vetülete (3. ábra). Ekkor

DV = As.

Látható, hogy egy test, kiterjedése változatlansága esetén, bármely irányba azonos nagyságú tértartományt járhat be úgy, hogy az adott irányú elmozdulás nagysága (a newtoni értelemben vett út) eltérő, mert függ az elmozdulásra merőleges felülettől. Tehát Descartes megalapozottan állította, hogy a felületnek is van szerepe a mozgásban, de nem a súrlódás és ellenállás szempontjából, ahogy kritikusai gondolják.

Az idő és a sebesség karteziánus felfogása

Az idő értelmezése a Filozófia alapelveiben nem teljesen egyértelmű. Descartes nem sok szót veszteget rá, csupán az I. részben említi. Az állítja, hogy a „tartam”-ot a priori ismerjük meg. A tartam „az a módusz, avagy módozat, ahogyan ezt a dolgot mint folyamatosan létezőt tekintjük” [9]. A tartam ideája világosan elkülönül a szubsztancia ideájától. Ugyanakkor a következő pontban azt is kijelenti, hogy a módusz valójában atributum. Így a teremtett dolgok esetén „.... azt, ami mindig ugyanazon a módon van meg bennük, mint ahogyan a létezés és a tartam abban a dologban, amelyik létezik és tart, atributumnak, .... fogom nevezni” [10]. Így a dolog időbelisége a létezéséből, illetve létezése és önmaga folytonosságából következik.

Ezért a dolgok időbelisége, „tartama” benne van a dologban (testben). Az isteni örökkévalóság és a dolgok létideje azonban az ember számára érzékelhetetlen, ezért a tudományos megismerés során ez az „abszolút idő” nem használható. Descartes szerint nem tévesztendő össze azzal az idővel, „....amelyet megkülönböztetünk az általánosságban vett időtartamtól, és a mozgás mértékének mondunk, (mert ez) csak egy bizonyos módozat, ahogyan ezt a tartamot elgondoljuk” [11]. Ebben az értelemben az idő a gondolkodás módozata, ahogy az elme a világot szemléli. Amíg a „létezés ideje” valamennyi dologban azonos, addig a gondolkodás módozataként tekintett idő eltérő és korlátozott hatókörű lehet [12]. Hogy a szemlélet számára összehasonlítható legyen, bizonyos speciálisan mozgó testeket jelölünk ki az idő mérésére. „Ám hogy azonos mérték szerint foghassuk fel valamennyi dolog³ időtartamát, rendszerint egyes szabályos mozgások  időtartamát használjuk, mint amilyen a nap és az év, s ezt hívjuk, miután az időtartamot ily módon összehasonlítottuk, időnek.” [13] ⁴

Tehát az idő, minta dolgok létezési ideje egységes és létezik. De ez az idő az ember számára érzékelhetetlen, a világ megismerése során csak a dolgokat, ezek mozgását, változását látja, és ez alapján értelmezi, fogja fel az időt. A mechanikus filozófia ugyanis mind a jelenségek magyarázatát, mind az érzékelést láthatatlan, kicsiny részecskék mozgására vezeti vissza. Mivel az időt nem a priori fogjuk fel, csak tapasztalatainkra, érzékeinkre támaszkodhatunk.⁵ Ezek a tapasztalatok azonban, és maga az érzékelés is, miként a világ összes jelensége, szintén a részecskék mozgására, így végső soron a kiterjedésre vezethetők vissza.

Descartes, miként Arisztotelész is, úgy vélte, hogy vákuum nem létezhet, mert logikai ellentmondáshoz vezetne [16]. (Szemben például az atomistákkal és Newtonnal.) A mozgó test a vákuummentesen kitöltött térben az egyik helyről a másikra folytonosan halad, úgy, hogy a test két állapotában elfoglalt helye közti tér egészét bejárja. Mind a test által elfoglalt, mind a bejárt térrész kiterjedés, azaz végtelenül osztható, így tetszőlegesen kicsiny elmozdulás, ezáltal tetszőlegesen kicsiny időpillanat is értelmezhető. Ahogy a mozgás, úgy az idő is folytonos. Az idő mérése úgy történik, hogy a tetszőlegesen kiválasztott, de szabályos (ismétlődő, azonos) mozgást végző időmérő test pályáján bizonyos meghatározott helyeket jelölünk ki (pl. inga végpontjai)⁶ egy adott vonatkoztatási rendszerben, és más testek mozgását ahhoz viszonyítjuk, hogy az időmérő test a meghatározott pálya mekkora hányadátjárt a be a vizsgált mozgás során. Így az idő mérése a kiterjedés mérésére, illetve kiterjedések arányára vezethető vissza (4. ábra).

Fel kell ismerni, hogy az idő emberi érzékelése szorosan kapcsolódik a mozgáshoz.⁷ Ha nincs érzékelhető mozgás, akkor az idő sem mérhető, illetve ismerhető fel az ember számára. Ez egyaránt igaz akkor, ha valóban nincs mozgás, de akkor is, ha a megfigyelőhöz kötött vonatkoztatási rendszer együtt mozog a megfigyelt testekkel, így azok „látszólag” nyugalomban vannak.

A sebesség

A sebességet a karteziánus fizikában is az elmozdulás és az „ehhez szükséges idő” hányadosaként értelmezhetjük. Az eltérés a sebesség mai felfogásához képest abban áll, hogy a test elmozdulását nem az út, hanem a mozgás során bejárt tér nagysága jellemzi. A bejárt térrész, mint kiterjedés, skalár mennyiség (gyakorlatilag egy hasáb térfogata). Az idő, mint a „mozgás tartama” dimenzió nélküli mennyiségként értelmezhető, azt mutatja, hogy az időmérő test által bejárt térrész hogy aránylik ahhoz a térrészhez, amit ez a test egy periódus alatt jár be. A kettő hányadosa, azaz a sebesség is skalár érték lesz.

Jelölje c (mint celeritas) a sebességet a karteziánus fizikában. A következő egyenleteket írhatjuk fel:⁸

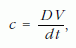
ahol

Ebből képezhető egy adott irányra vonatkozóan megadott  (vagy adott felületre merőleges) sebesség is (eltérés a newtoni sebességhez képest az idő értelmezésében van):

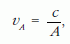
ahol v_A az A felületre merőleges irányban mért sebesség,

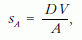
ahol s_A az A felületre merőleges irányban mért elmozdulás.

A sebesség nagyságának és irányának függetlensége

Mi az előnye annak, ha a sebességet nem mint a pillanat alatt megtett utat, hanem mint a pillanat alatt bejárt térrészt határozzuk meg? Egyrészt teljesen összhangba kerülünk a descartes-i szövegekkel, másrészt fel tudunk oldani egy látszólagos ellentmondást a karteziánus fizikában. Ez az alábbi két állítás összeegyeztethetetlenségéből ered, amelyek egyike a mozgásmennyiség meghatározását adja [17], a másik a test sebességének és irányának (determináció) függetlenségét mondja ki [18].

A Filozófia alapelvei II. rész 43. pontjában Descartes a testek „erejét” vizsgálja, amivel képesek „hatást kifejteni”. Minden testnek van egy „tehetetlenségi ereje”, hogy ellenálljon állapota és helyzete megváltoztatásának. Ez a változás Descartes szerint lehet egyrészt két test elválasztása és az összekapcsolása (azaz vagy a korábban együtt mozgó testek eltávolodnak, vagy a korábban eltérően mozgó testek együtt fognak mozogni, így egymáshoz viszonyított relatív elhelyezkedésük változik), másrészt nyugvó test mozgásba hozása, vagy mozgó test megállítása (állapot). A mozgásmennyiség azt fejezi ki, hogy mekkora hatás kell egy adott test relatív helyzetének megváltoztatásához. Félreérthető, hogy ezt a mozgásmennyiséget Descartes egyik alkalommal két összetevő, a kiterjedés és a sebesség szorzataként határozza meg [19], máshol azonban e kettőn túlmenően megemlíti még befolyásoló tényezőként a két testet elválasztó felület nagyságát és az ütközések módját is, amiből egyes kritikusai arra következtetnek, hogy szükséges az alakból eredő „súrlódás” figyelembe vétele is, amit Descartes már elmulasztott.⁹

Ugyanakkor Descartes a Filozófia alapelvei II. rész 41. pontjában azt állítja, hogy téves felfogás, ha a mozgáshoz hozzákapcsoljuk a test adott mozgásirányba való determinációját, azaz a mozgás irányát a mozgás fogalmához tartozónak gondoljuk. Nála a mozgás mozgásmennyiség, mérhető, a kiterjedésre visszavezethető dolog, független a test determinációjától (skalár mennyiség). Egy mozgó test mozgási irányának változása elkülönül a mozgásmennyiségének változásától. A test tehát minden további nélkül képes irányának megváltoztatására, amint környezete erre kényszeríti, miközben sebessége és mozgásmennyisége nem változik. Ha azonban elképzelünk egy nagy felületű, lapos testet (5. ábra), akkor a hagyományos sebességfelfogás és változatlan kiterjedés esetén a felületre merőlegesen, illetve vele párhuzamosan mozogva, azonos elmozdulás esetén a megmozgatott térfogat, és hétköznapi intuíciónk alapján az ellenállás is, jóval nagyobb lenne, mint az elsőként említett esetben. Ezzel szemben az általam javasolt sebesség értelmezést használva a pillanat alatt bejárt térrész (sebesség) állandósága lehetséges az ellenállás megnövekedése nélkül is, mertekkor a kisebb felülethez nagyobb elmozdulás, míg a nagyobbhoz kisebb elmozdulás tartozik. (Elmozduláson a mozgás irányába eső utat értem.)

A felület szerepe

Ezáltal érthetővé válik a felület szerepe, anélkül, hogy a Descartes kritikusai által szükségesnek vélt súrlódó erő létét feltételeznénk. A felület jelentőségét nem az adja, hogy a sebességen és a kiterjedésen túl részt vesz a mozgásmennyiség meghatározásában, hanem az, hogy az általam megadott, illetve a hagyományos értelemben vett sebesség, elmozdulás között is felállítható egy arányosság: „Hasonlóképp, amikor a test nyugalmi állapotban van, akkor van ereje ahhoz, hogy megmaradjon ebben a nyugalomban, és ellenálljon mindennek, ami azt megváltoztathatná. Amikor mozog, akkor ugyanígy van ereje hozzá, hogy ugyanazzal a sebességgel és ugyanabba az irányba mozogjon. Ámde ennek az erőnek a mennyiségéről csak úgy ítélhetünk, hogy beszámítjuk a test nagyságát, amelyben az erő előfordul, és a felület nagyságát, amely ezt a testet egy másiktól elválasztja, de a mozgás sebességét is, valamint azokat az ellentétes módozatokat, ahogyan több különböző test egymással találkozik.” [21]

Mivel más szöveghelyekből egyértelműen az derül ki, hogy a mozgásmennyiség a kiterjedés és a sebesség szorzata, jogos a kérdés, milyen szerepe van a felületnek. Előbb azonban pontosítsuk, mit is értett Descartes felületen. A két testet, szükségképpen a mozgó testet és a mozgás irányába eső szomszédját (szomszédait), elválasztó felület, illetve ennek a mozgás irányára merőleges komponense (ha felbontjuk a Descartes által a Filozófia alapelvei II. rész 32. pontjában bemutatott módon merőleges összetevőkre) ugyanis nem más, mint az MM = Qc = QAs képletben szereplő A felület. Ha tehát egy adott mozgásmennyiségű test olyan irányba mozdul el, amerre merőlegesen a felülete kisebb, nagyobb utat fog megtenni, azaz nagyobb lesz a newtoni értelemben vett elmozdulása. Így ez az elmozdulás (és a belőle származtatott sebesség) irányfüggő (a test irányra merőleges vetületétől függő), míg ezzel ellentétben a test karteziánus értelemben vett elmozdulása és sebessége nem fog megváltozni a determináció változásával, arra invariáns. A testek viszont csak akkor képesek együtt mozogni egy adott irányba, ha az adott irányú elmozdulásuk megegyezik. Ez az elmozdulás az MM/QA hányados, azaz a test „tehetetlensége” valóban a descartes-i szövegben megadott paraméterektől, többek közt a felülettől is, függ (6. ábra).

Miután így sikerült számot adni a Filozófia alapelvei II. rész 43. pontjában felsorolt, a mozgásmennyiséget befolyásoló változók többségéről (a test kiterjedése: Q, az elválasztó felület nagysága: A, a mozgás sebessége: c), a fennmaradók pedig (a test környezete és az ütközések változatos módjai) a determináció meghatározásában kapnak szerepet, belátható, hogy nem szükséges új, Descartes fizikájában nem szereplő entitások bevezetése.¹⁰

Nyilvánvaló, hogy tévesek azok a kritikák is, amelyek azt állítják, hogy a descartes-i fizika hét ütközési törvénye kevés a változatos jelenségek leírására. Ha meggondoljuk, hogy az ütköző testek mozgásmennyisége, sebessége, kiterjedése, ütköző felülete egyaránt lehet a domináns test (általában az ütközési törvényekben a B test) vonatkozásában kisebb, nagyobb vagy egyenlő, akkor máris 3⁴ = 81 variációs lehetőségünk van, amit tovább fognak bővíteni a determinációt érintő megfontolások.¹¹

Összefoglalás

Bemutattam, hogy a paradigmaváltások során tapasztalható félreértelmezések a rivális paradigmák közt is fennállnak, ami megnehezíti a vesztes paradigma fogalmi struktúrájának utólagos feltárását. A fogalmak értelmének, és a mögöttük húzódó ontológiai feltételek pontos ismeretének hiánya szükségszerűen hamis képetad a paradigmáról, ezértelengedhet etlen a gondos és alapos feltárásuk.

A descartes-i fizika sem értelmezhető helyesen a mai fogalmakkal. Egy olyan fogalmi keretben, ahol az idő nem alapmennyiség, és a testeket csupán a kiterjedésük határozza meg, a sebesség megszokott fogalmát sem lehet használni. A test nem modellezhető tömegpontja sebességével, mozgása nem ábrázolható vonallal. Az a priori fizika elmozdulása és sebessége a két egymást követő állapotban elfoglalt hely közti térrésszel (mint bejárt tértartománnyal) határozható meg. A legnagyobb különbség mégis abban áll, hogy a skalár mennyiségként értelmezett sebesség esetén meg kell tudni magyarázni, miként lehet értéke az eltérő irányokban azonos. Ezt csak akkor tudjuk ad hoc hipotézisek nélkül elérni, ha az elmozdulást mint bejárt térrészt értelmezzük.

Bár Descartes maga nem írta le fizikáját matematikai egyenletek formájában, megmutattam, hogy lehetséges a karteziánus fizikában mozgásegyenletek felállítása, és segítségükkel példák megoldása és tételek bizonyítása.

Ugyanakkor számos nyitott kérdés maradt. A forgó, vagy az egyenes vonalú, egyenletesen gyorsuló mozgás leírása, és összhangba hozása Descartes gravitációs elméletével, vagy az összetett testek mozgásának elemzése még megoldásra vár. Éppúgy, ahogy a mozgásmennyiség megmaradás és átadás, illetve a mozgó testek gyűrűjében lejátszódó folyamatok feltárása is. Ha figyelembe vesszük, hogy a newtoni paradigmát kétszáz éven keresztül pontosították, akkor könnyen belátható, hogy egy hosszú folyamat kezdetén vagyunk, hisz a karteziánus fizika normál kutatási szakasza még csak most kezdődött el.

Irodalom

1.    -->
1. Boros G.: A mozgástörvényektől Isten értelmi szeretetéig. Áron Kiadó, Budapest, 2003.
2.    -->
2. Kvasz L.: Newton (anti)kartezianizmusa. Kellék 32 (2007) 83-93.
3. D. M. Clarke: The Impact Rules of Descartes’s Physics. In René Descartes. Critical Assessments. (szerk. Georges J. D. Moyal) Routledge, London (1991) 110-122.
4. E. Slowik: Cartesian Spacetime. Kluwer Academic Publishers, London, 2002.
5. Clarke: op. cit. [3]
6. ugyanott 113-114.
7. R. Descartes: A filozófia alapelvei. (ford. DékányAndrás) Osiris Kiadó, Budapest (1996) II. 37, 39.
8. ugyanott 149. Kiemelés tőlem. Eredeti szöveg: R. Descartes: Le Monde. In Oeuvres de Descartes XI. (szerk. Charles Adam és Paul Tannery) Vrin, Párizs (1986) 39-40.
9. ugyanott I. 55.
10. ugyanott I. 56.
11. ugyanott I. 57.
12. Szamosi G.: A polifón zene és a klasszikus fizika, a newtoni időfogalom eredete. Fizikai Szemle 41/8 (1991) 266-268. Eredeti cikk: History ofScience 1990/28 175-191. (ford. Abonyi Iván)
13. Descartes: op. cit. [7] I. 57.
14. B. Spinoza: Descartes’ Prinzipien der Philosophie aufgeometrishe Weise begründet. Felix Meiner Verlag, Hamburg (1987) 120-121.
15. C. Larmore: Descartes’ Empirical Epistemology. In Descartes: Philosophy, Mathematics and Physics. (szerk. S. Gaukroger) The Harvester Press, Sussex (1980) 6-22.
16. Descartes: op. cit. [7] II. 16-19.
17. ugyanott II. 43.
18. ugyanott II. 41.
19. ugyanott II. 43.
20. Clarke: op. cit. [3] 114.
21. Descartes: op. cit [7] II. 43. (Kiemelés tőlem.)
22. Clarke: op. cit. [3] 115.
23. Spinoza: op. cit. [14] 86-88.

 1 A „mechanikus filozófia” kifejezés állítólag R. Boyle-tól származik. A tudományos magyarázat 16-17. században kialakult irányzata, amely a korábban uralkodó arisztotelészi filozófiával ellentétben a világ jelenségeit kicsiny (láthatatlan) részecskék mozgására próbálta visszavezetni. Az Univerzumot mint gépezetet képzelte el, ami felépítésének és szabályainak megfelelően működik (lásd az órametaforát). Egyes gondolkodók, mint például Descartes is, az élőlényeket, illetve az emberi testet is mint gépezetet képzelték el. Bővebben lásd Boros Gábor munkáját[1].

2 A cikkben nem foglalkozom a karteziánus fizikában a jelenségekért felelős apró testek tulajdonságaival, de meg kell említeni, hogy változatos alakúak és méretűek (ami alapján 3 alapvető csoportba sorolhatók), tökéletesen merevek és azonos, homogén anyagból állnak.

3 A véges emberi elme számára felfogható „valamennyi” dolog.

4 Spinoza a Filozófia alapelveihez írt magyarázatában világosabban fogalmaz: „Hier sage ich nur, dass sie (die Ewigkeit) das Attribut ist, unter dem ich das unendliche Dasein Gottes begreife, dagegen ist die Dauer das Attribut, unter dem ich das Dasein der erschaffenen Dinge, so wie sie in der Wirklichkeitbeharren, begreife. Daraus folgtklar , dass die Dauer von dem ganzen Dasein eines Dinges nur dem Gesichtspunkt des Denkens nach unterschieden wird, da man das, was man der Dauer eines Dinges abzieht, auch seinem Dasein abziehen muss. Um dies zu bestimmen, vergleicht man es mit der Dauer der Dinge, die eine feste und bestimmte Bewegung haben, und nenntdiese Vergleichung die Zeit. Daher ist die Zeit keine Bestimmung der Dinge, sondern nur eine Art, sie zu denken, ....” [14] („Itt csak azt állítom, hogy az örökkévalóság csupán egy attributum, amivel Isten végtelen létét megragadom, ellentétben a tartammal, ami az az attributum, amivel a teremtett dolgok létét ragadom meg, úgy, ahogy a valóságban fennállnak. Ebből világos, hogy egy dolog egész létének tartama csak a gondolkodás nézőpontjából különböztethető meg, mivel amit bárki egy dolog tartamának tekint, azt saját létére kell vonatkoztatnia. Ezt meghatározandó, olyan dolgok tartamához hasonlítja, amelyeknek rögzített, meghatározott mozgásuk van, és ezt az összevetést nevezi időnek. Így az idő nem a dolog meghatározója, hanem csupán a gondolkodás egy módozata.” Fordítás tőlem.) További érvelés található a lét és a jelenlét megkülönböztetéséről ugyanitt, a 128-130. oldalon.

5 Descartes-nál a fizikai világot két irányból ismerjük meg. Az alapelveket, az „első okokat”, amelyek a világ legáltalánosabb tulajdonságait fejezik ki, a priori kell elsajátítani. Ezen a priori természeti törvények érvényességét az garantálja, hogy Isten létét csupán a priori módon, mindenféle tapasztalat nélkül képesek vagyunk igazolni. A valóság és a róla szerzett tapasztalatunk lehet bármilyen, ezen törvények igazsága a „cogito” bizonyosságában van. Azt, hogy a világ - aminek létére és milyenségére az ideáink alapján következtetünk - valóban létezik, és olyan, mint véljük, azt bizonyítja, hogy ideáinkat valamiképp passzívnak, külső tárgyak által keltettnek tapasztaljuk, és Isten létéből eredően garanciánk van arra, hogy amit tisztán és világosan igaznak érzékelünk, az valóban igaz. Ha tehát képesek vagyunk belátni, hogy létezik a tárgyaknak és a mozgásnak egy világa, akkor jogosan hisszük, hogy ez az a priori természettörvények által irányított fizikai világ. De Descartes is látta, hogy az a priori fizika nem képes teljes körűen leírni a világot. Az önevidens elvekből dedukcióval levezetve csak a világ legáltalánosabb szabályai állapíthatók meg, mint például, hogy a három fizikai törvényből levezethetők a testek ütközésének törvényei. Ezzel szemben a Filozófia alapelveiben Descartes felsorol néhányat azon számos jelenség közül, amelyek csak empirikus kutatással tárhatók fel. A legfontosabb ezek közül az anyag részecskéinek mérete, amekkora darabokra az anyagot Isten a világ teremtésekor felosztotta. A továbblépés az empirikus hipotézisek rendszerével lehetséges. A hipotézisek a descartes-i terminológiában a fizikai kutatás empirikus részéhez tartozó magyarázó tételek. Ha a hipotézisből levont következtetés megegyezik a tapasztalattal, különösen a döntő kísérletből nyert adatokkal, akkor minden okunk megvan, hogy a hipotézist igaznak véljük. Tehát a hipotetikus-deduktív módszer a descartes-i fizika empirikus oldalához tartozik. Nem érinti az alapvető természeti törvényeket, és ha hamisnak bizonyul, nem is érvényteleníti azokat. Az empirikus hipotéziseket pedig vagy a priori demonstrációra vezetjük vissza, vagy a módszertani elveknek megfelelően az összes lehetséges, alternatív hipotézist feltárjuk, és döntő kísérletekkel a számukat a legkisebbre, lehetőleg egyre csökkentjük.

A hipotetikus-deduktív módszer segítségével lehetővé válik a meglévő elméletek és a hipotézisek igazolása, illetve az a priori és a tapasztalati tudáselemek egységes rendszerbe foglalása. Mindehhez kell, hogy az empirikus kutatás megkezdése előtt az a priori terület a lehető legalaposabban kifejtésre kerüljön, mivel a kapott a priori törvényeket a későbbiekben minden szóba jöhető hipotetikus rendszernek teljes egészében tartalmaznia kell. Ezek, és a megismerés alapelvei bizonyos kötöttségeket tartalmaznak a magyarázat elfogadható módjára, a legfontosabb problémákra, és a megoldásokra vonatkozóan. (Bővebben lásd C. Larmore cikkében [14].)

6 Az inga mozgása nem egyenletes, hanem szabályosan ismétlődő, azonos elmozdulással

7 El lehet különíteni az isteni örökkévalóságot, a testek létezési (abszolút) idejét, és az ember számára érzékelhető időt (tartam). A fizikában csak ez utóbbi vizsgálható.

8 Csak a karteziánus fizika törvényeinek részletes kidolgozása során lenne eldönthető, hogy praktikusabb lenne-e a sebességnek egy, az általam megadottal egyenértékű, de eltérő definíciója. Vonatkoztathatnánk például egységnyi kiterjedésű test elmozdulására (DV/Q), de akár az időt is tekinthetnénk kiterjedésnek (DVidőmérő).

9 „.... if M has a larger surface area than N, then it will encounter more resistance from the medium in which they move, and to compensate for this M needs a greater impressed force to maintain the same speed as N. Since the first kind of resistance to motion is a characteristic of a body apart from the medium in which it moves.” [20] („.... ha M felülete nagyobb, mint N-é, akkor sokkal nagyobb ellenállást fejt ki rá az a közeg, amiben mozog, és ezt ellensúlyozandó, M-nek nagyobb hatóerő szükséges, hogy N-ével azonos sebességgel mozogjon. Ám az ellenálló képesség első fajtája [értsd: a mozgásmennyiség a Filozófia alapelvei II. 43. alapján] a test kizárólagos sajátossága, a mozgás közegétől függetlenül.” Fordítás tőlem.)

10 Téves Clarke állítása: „So there is one kind of inertia which depends on the quantity of matter and another which depends on the extension of their surfaces.” [22] („Így létezik az inerciának egy olyan fajtája, ami az anyag mennyiségétől [a kiterjedéstől] függ, és egy másik, ami a felülete nagyságától.” Fordítás tőlem.)

11 A nem egyenes vonalú ütközések vonatkozásában lásd a Filozófia alapelvei II. 32. pontját [7], illetve Spinoza kommentárjait a ferde ütközésekről [23].