
Fizikai Szemle honlap |
Tartalomjegyzék |
Károlyházy Frigyes több mint fél évszázadon át volt tagja az Eötvös-verseny versenybizottságának. Ő maga diákkorában nem indult ezen a versenyen, mivel amikor érettségizett, már éppen szétszakadóban volt a versenyt jegyző Eötvös Loránd Matematikai és Fizikai Társulat, és nem rendezték meg a versenyt. A matematikusok külön társulatot hoztak létre Szegeden, a fizikusok pedig éppen csak ébredeztek a kábulatból, amelyet például Ortvay Rudolf elvesztése okozott. Selényi Pál, akinek aktív szerepe volt a fizikai társulat háború utáni megalakításában, a nála munkára jelentkező Vermes Miklóst bízta meg a fizikai tanulóverseny megszervezésével. Vermes kimutatása szerint az első hivatalos fizikai Eötvös-versenyt 1949-ben rendezték, amikor Károlyházy Frigyes már másodéves hallgató volt az egyetemen, ezért nem is indulhatott rajta. Ő ugyan emlegetett egy előző évben tartott versenyt, amelyen elindult és amelyen sikeresen szerepelt, sőt még arra is emlékezett, hogy Sós Vera is indult a versenyen, de lehet, hogy az matematikaverseny volt és semmi írásos nyoma nem maradt.

Hogyan került Károlyházy Frigyes a versenybizottságba? Kezdetben Selényi Pál, majd Pócza Jenő volt a versenybizottság elnöke, 1959-től lett Vermes Miklós, aki addig is a verseny szervezője, mindenese volt. Valószínűleg még Pócza idejében történt, hogy nem sokkal a verseny után valaki felhívta Vermest telefonon és az egyik feladat megoldása iránt érdeklődött. Vermes évtizedekkel később is kuncogva mesélte el a történetet: az illető azt kérdezte, hogy ugye az ennek a feladatnak a megoldása, hogy… – és elmondta a megoldást, amire a bizottság gondolt. – Ugyanis az a helyzet – mondta az illető rendkívül tapintatosan –, hogy az úgy nem jó. Az illetőt Károlyházy Frigyesnek hívták, akit Vermes már a következő évben behívott a versenybizottságba. Ezután már csak egyetlen évben engedte meg neki, hogy távol maradjon, amikor tanulmányúton volt az Egyesült Államokban, 1974-ben. Ekkor hívta meg a bizottságba Vermes e sorok íróját.
Károlyházy és Vermes kiegészítették egymást. Károlyházy menekült minden adminisztratív tevékenység elől, ezt rábízta Vermesre, aki viszont bátran rábízta magát Károlyházy fizikai szemléletére, meglátásaira. Ők ketten minden alkalomra kirukkoltak egy-egy nehéz feladattal, olykor többel is, hogy tudjon miből választani a bizottság. Vermes általában számításos feladatokat hozott, amelyek megoldásához biztos tárgyi tudásra és problémamegoldói gyakorlatra volt szükség, Károlyházy viszont majdnem mindig "meglepő" feladatokkal érkezett, amelyek megoldásához kreativitás kellett. Ezen feladatok közül fogunk most válogatni. A régi versenyzőknek alkalmuk lesz nosztalgiázni, a fiatalok pedig megismerhetik azt a fizikus gondolkodásmódot, ahogyan Károlyházy Frigyes nézte – és nézni tanította – körülöttünk a világot.
Több mint 50 éve, 1961-ben szerepelt Eötvös-versenyen a következő Károlyházy-feladat.
Ostornyél egyik végére vékony cérnaszálon elenyésző tömegű tollpihét kötünk, és körbe forgatjuk. Milyen pályán mozog a pihe?
Megoldás. A pihére jellemző, hogy nincs tömege, súlya, és csak a légellenállási erő hat rá. Az R hosszú pálca végéhez L hosszúságú fonálra kötött pihére a légellenállási erő a sebesség irányával ellentétesen hat, tehát a fonál iránya a pihe pályagörbéjének érintője. A bot vége R sugarú kört ír le, ezért ha L < R, akkor a pihe is körpályán mozog, amelynek x sugarát Pitagorasz tételével számíthatjuk ki:
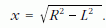
Ha a cérna hosszabb, mint a pálca, akkor nincs stabil pálya.
1972-ben a következő kérdést tette fel Károlyházy Frigyes.
Felfújt, könnyű műanyag labdát találomra megpörgetve sima vízfelületre ejtünk. Azt tapasztaljuk, hogy mielőtt megáll, rendszerint függőleges tengely körül forog. Mi a jelenség magyarázata?
Megoldás. A ferde helyzetű tengely körüli forgás vízszintes és függőleges tengely körüli forgás eredőjeként fogható fel. A vízszintes tengely körüli forgást a súrlódás erősen fékezi, mert a gömb "egyenlítője" mentén nagy a sebesség, és emiatt nagyobb a folyadékban a súrlódás. A függőleges tengely körüli forgásnál az érintkező felület kis gömbsüveg, ahol a sebesség és így a súrlódás is kisebb; a forgásnak ez az összetevője lassabban fékeződik le, és idővel már csak ez érvényesül.
1985-ben egy igazi gravitációs feladatot adott fel.
Egy U alakú csőben folyadék van egyensúlyban. Ezután a bal oldali szár alá igen nagy tömegű golyót helyezünk. Hogyan változnak meg a folyadékszintek?
Megoldás. A közlekedőedény folyadékfelszínei nívófelületen helyezkednek el, ezek eredetileg vízszintes síkok. A nagy tömegű golyó odahelyezése után a nívófelületek jobb oldalt kissé lefelé hajlanak, tehát a folyadékszint a bal oldali szárban kissé emelkedik, a jobb oldalon süllyed.
1989-ben pedig egy, a mindennapi életből ellesett problémával lepte meg a versenyzőket.
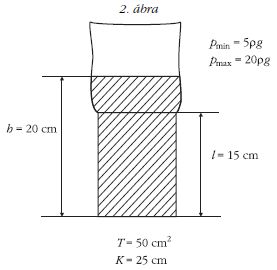
Gergő gyakran segít a háztartásban. A zacskós tejet az 1. ábrán látható módon a zacskónál valamivel szűkebb keresztmetszetű, levágott tetejű és alul kilyukasztott műanyag flakonban szokták tárolni. Gergő megfigyelése szerint a szájával lefelé fordított flakonból a még felbontatlan zacskós tej magától kiesik, viszont a tetejénél megfogott tejes zacskóról még akkor sem esik le a flakon, ha alulról egy másik zacskó tejet akasztunk rá. Mi lehet a magyarázat?Megoldás. A flakont a súrlódási erő tartja meg. A súrlódási erő a flakon falára ható nyomóerővel arányos, ez a nyomóerő pedig a tej hidrosztatikai nyomásából származik. A súrlódási erő nagyságát becsléssel állapítjuk meg. Azt kell megmutatnunk, hogy a flakonra ható súrlódási erő az ábrán látható helyzetben 10 N-nál is nagyobb lehet, viszont a szájával lefelé fordított flakonban a tejeszacskóra 10 N-nál kisebb súrlódási erő hat.
Most egy becsléssel megmutatjuk, hogy ez teljesül. Az egyszerűség kedvéért mérjük a távolságot centiméterben (2. ábra). A tejeszacskó kerülete valamivel kisebb, mint 25 cm, ezért a flakonban a zacskó kissé meggyűrődik, így a tej egyenletesen nyomja a zacskót a flakon falához. A zacskóban a tej fölött levegő van, ennek nyomása megközelítőleg egyenlő a külső légnyomással. Esetleg még nagyobb is lehet, ha – miközben tartjuk – jól meg is szorítjuk a zacskót. Ezzel a nyomóerőt és így a súrlódási erőt is tovább növeljük. Most azonban ezt ne vegyük figyelembe; e nélkül is meg kell tartsa a flakont (a ráakasztott másik zacskó tejjel együtt) a súrlódási erő.
 |
 |
Mivel a hidrosztatikai nyomás lefelé lineárisan nő, átlagos értéke a 2. ábra alapján:
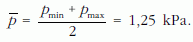
A flakon falának területe:
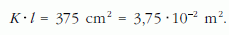
E kettő szorzatának μ0-szorosa adja meg a súrlódási erő maximális értékét. (μ0 a tapadási súrlódási együttható, amelynek értéke legalább 0,3 és legfeljebb 0,6 a zacskó és a flakon fala között.) A legkisebb μ0 értéket véve is:
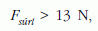
tehát a súrlódási erő valóban meg tudja tartani a mintegy 10 N súlyú másik zacskó tejet.
A feladat megoldása akkor teljes, ha azt is megmutatjuk, hogy a lefelé fordított flakonból magától kiesik a tejeszacskó, még a lehető legnagyobb μ0 esetén is.
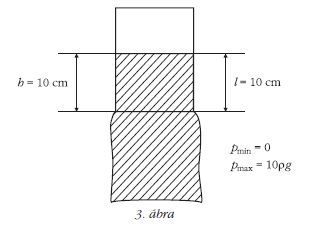
Tegyük fel, hogy a lefelé fordítás után a zacskó még nem mozdult el, csak a tej ömlött át a zacskó alsó részébe (3. ábra). A flakon falára ható hidrosztatikai nyomás átlagértéke most csak
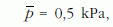
és ez a kisebb nyomás ráadásul kisebb területen is hat a flakon falára:
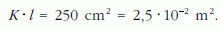
E két érték szorzatának μ0-szorosa még μ0 = 0,6 esetén is csak 7,5 N, tehát
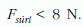
Ezért a tejeszacskó kiesik a lefelé fordított flakonból.
Megjegyzés. A megoldáshoz tartozik μ0 értékének becslése is. A példaképpen bemutatott gondolatmenetben a 0,4 ≤ μ0 ≤ 0,6 becslést alkalmaztunk, ez összhangban van a Középiskolai Fizikai Táblázatokban, illetve középiskolai és egyetemi tankönyvekben közölt adatokkal. Ugyanakkor, ha a tejeszacskó kívül zsíros, μ0 jóval kisebb is lehet, s a zsíros tejeszacskóról bizony lecsúszhat a flakon a ráakasztott másik liter tejjel együtt. Most azonban nem erről a tapasztalatról volt szó, nem ezt kellett megmagyarázni.
Látjuk, a fenti feladat megoldásához már némi számolásra, numerikus becslésre is szükség volt. 1992-ben viszont ismét elég volt "csupán" gondolkozni a problémán.
Körülbelül 1 cm2 keresztmetszetű, 80 cm hosszú, felül nyitott üvegcsövet színültig megtöltünk higannyal. A cső felső végére ráhúzzuk és befőttes-gumival a csőhöz szorítjuk egy teljesen összelappadt (levegőt nem tartalmazó) lufi száját. Ezután a csövet a levegőben tartva felfordítjuk. Mi fog történni? (Készítsen rajzot is!)
Megoldás. Feltételezhetjük, hogy amikor az összelappadt lufit ráhúzzuk az üvegcső szájára, a higany feletti részben nem lesz levegő, és később sem tud bejutni levegő a lufi belsejébe.
Fordítsuk meg a csövet! Függőleges helyzetben a cső – most már alul levő – szájánál a lufihártyára belülről 80 cm magas higanyoszlop nyomása, kívülről pedig a külső levegő nyomása hat. (Vegyük ez utóbbit 76 Hgcm-nek.) A belső, nagyobb nyomás kissé szétnyitja az összelappadt lufit, s a higany elindul lefelé. 80-76 = 4 cm3 higany lefut egészen a lufi aljára, és ekkor a folyamat leáll. A csőben marad 76 cm magas higanyoszlop, fölötte vákuum (a higanygőz nyomása elhanyagolható). Alul, a cső szájától kezdve a lufi újra összelappadt állapotban van, mert a külső légnyomás összenyomja. Legalul, az összelappadt lufiban lévő 4 cm3 higany kicsi, kidudorodó zacskóban gyűlik össze.
A folyamat legfontosabb pillanatait a 4. ábra sorozata szemlélteti ("oldalnézetben").
Ha túl gyorsan fordítjuk meg a csövet, esetleg a végén még meg is lökjük kissé, 4 cm3-nél több higany is le tud folyni a lufi aljára. Ekkor a végállapotban a külső légnyomás kissé visszanyomná a lufit a cső szájánál a cső belseje felé. Ugyanakkor a lufit a higany lefelé húzza, kissé megnyújtja a gumit, s ez a hatás a cső szájánál is érvényesül. Mindezek azonban olyan kicsiny nyomáskülönbséget és többleterőt eredményeznek, hogy a lufinak ebből származó alak változása szabad szemmel alig vehető észre, s a megoldást lényegesen nem módosítja.
Károlyházy Frigyes figyelmét nem kerülte el az űrhajózás sem, és egy sajátos problémát vetett fel 2003-ban.
Egy szabadon keringő űrhajó kabinjának belsejében mozdulatlanul lebeg egy körülbelül 4 cm átmérőjű vízgolyó és a közelében egy körülbelül 8 cm hosszúságú, vékony, kör keresztmetszetű, legömbölyített végű üvegpálca. A pálca egyik végét egészen finoman érintkezésbe hozzuk a "vízcseppel". Vázolja fel, milyen alakot vesz fel a víz!
Megoldás. A kiindulási helyzetben (5.a ábra) a vízgolyó közelében lebeg az üvegpálca.
A folyamat akkor kezdődik, amikor a pálca egyik végét egészen finoman érintkezésbe hozzuk a vízcseppel (5.b ábra). A víz nedvesíti az üveget, kissé "ráfolyik" a pálca legömbölyített végére (5.c ábra). Itt azonban a folyamat nem állhat le, mert az üvegpálcára ható erők eredője nem nulla. Igaz ugyan, hogy az R sugarú vízcsepp belsejében a nyomás egy kicsit nagyobb, mint a külső légnyomás (Δp = 2α/R), és ez r2πΔp erővel tolná kifelé az r sugarú pálcát, de ennél sokkal nagyobb a pálcára rásimuló vízhártya által kifejtett 2rπα nagyságú húzóerő. A pálca tehát benyomul a vízcseppbe, egy közbülső helyzet a 5.d ábrán látható.
Az erőegyensúly ebben a helyzetben sem áll fenn, nincs ok, amiért a pálca megállna, egészen a 5.e ábrán látható állapotig. Most már a pálca elérte a vízcsepp bal oldali szélét, kissé túl is ment rajta, a vízfelszín itt kissé kinyomódik. Az erőegyensúly azonban csak akkor áll be, amikor a pálca bal oldali vége teljesen kibújik a vízcseppből, ekkor a pálca mindkét végét körülölelő víz felszíne ugyanolyan alakú (5.f ábra).
Meg kell gondolnunk még, hogy vajon a vízcsepp nem folyik-e szét a pálcán. A rendszer összenergiája a levegővel érintkező víz felületi energiájának és a vízzel érintkező üveg energiájának összegével egyenlő; ez a mennyiség igyekszik minél kisebb lenni. Tekintettel arra, hogy a pálca vékony, a üveg teljes felülete elhanyagolható a vízgolyó felületéhez képest. A rendszer egyensúlyát tehát a legkisebb vízfelszín követelménye határozza meg, ez pedig (adott térfogatú víz esetén) a gömb alaknál teljesül.
A végállapotban a vízgolyó majdnem pontosan gömb alakú, az üvegpálca ezen gömb egyik átmérője mentén helyezkedik el, és mindkét végét "kidugja" a vízből.
Egy év múlva szokatlan rugalmassági problémával állt elő, amelyet jellegzetesen "Károlyházy Frigyes módra" fogalmazott meg.
 Egy habókos lakberendező állófogast tervez, két változatban.
Egy negyedkörív
alakú, vékony, de erős, rugalmas
fémszálat egyik végénél
szilárdan hozzáerősít
egy merev törzshöz, egyszer
az a), másszor a b) elrendezésben
(6. ábra). Meglepődve
tapasztalja, hogy ha ugyanakkora terhet akaszt a
fogasokra, a fémszálak végpontja nem ugyanannyival
süllyed le a két esetben.
Egy habókos lakberendező állófogast tervez, két változatban.
Egy negyedkörív
alakú, vékony, de erős, rugalmas
fémszálat egyik végénél
szilárdan hozzáerősít
egy merev törzshöz, egyszer
az a), másszor a b) elrendezésben
(6. ábra). Meglepődve
tapasztalja, hogy ha ugyanakkora terhet akaszt a
fogasokra, a fémszálak végpontja nem ugyanannyival
süllyed le a két esetben.
Okoskodjuk ki egyszerű megfontolásokkal, hogy melyik esetben nagyobb a végpont lesüllyedése!
Megoldás. Vegyük észre, hogy a külső erő hatására a negyedkörív alakú rugalmas fémszál alakja fog megváltozni, pontosabban az erő által kifejtett (pontról pontra változó) forgatónyomaték okozza a szál alakjának megváltozását. A szál hosszának megváltozása (megnyúlása) elhanyagolható a szál alakjának megváltozása (lehajlása) mellett.
Célszerű lesz a két fémszál alakváltozását úgy összehasonlítani, hogy kölcsönösen egyértelműen megfeleltetjük egymásnak a két szál pontjait. A megfeleltetett pontokban fellépő deformációkat (elhajlásokat) hasonlítjuk össze, majd megvizsgáljuk, hogy ezek a deformációk milyen mértékben járulnak hozzá a végpontok lesüllyedéséhez.
Képzeljük – modellezzük – a rugalmas fémszálat nagyon kis szemekből álló láncnak, ahol az egyes (merev) láncszemeket piciny spirálrugók kapcsolják egymáshoz. A lánc (amelynek saját súlyát elhanyagoljuk) terheletlen állapotában pontosan negyedkört formál.
Írjuk fel, hogy mekkora forgatónyomatékot gyakorol a teher függőleges irányú G súlya a fémszálnak φ szöggel jellemzett helyén az ottani "spirálrugóra" (7. ábra )! (Ezen rugó elfordulása nyomán kialakuló visszatérítő nyomaték fogja majd G-nek azon a helyen fellépő forgatónyomatékát kiegyenlíteni, kompenzálni.)
Amint az az ábráról is leolvasható, ugyanazon φ szöghöz tartozó pontokban az M forgatónyomaték az a) esetben sohasem lehet kisebb a b) esetben fellépőnél, mivel sin? ≥ cosφ. Az egyenlőség csak φ = 0 és φ = π/2 esetben (vagyis a szál végpontjainál) áll fenn, közben Ma mindig határozottan nagyobb, mint Mb.
Ebből már látszik, hogy a fémszál deformációja (görbültségének megváltozása) minden bizonnyal az a) esetben lesz nagyobb. Azt kell még megnéznünk, hogyan jelentkezik mindez a szál végpontjának lesüllyedésében. Sejtésünk az, hogy a nagyobb deformáció nagyobb lesüllyedést is eredményez.
Vizsgáljuk meg, hogy ha csupán a φ szöggel megjelölt pontban jönne létre deformáció (ha csak az ottani kis spirálrugó csavarodna el), ez a végpont mekkora függőleges elmozdulását (lesüllyedését) eredményezné!
Az a) esetben a 8. ábrán látható 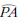 ív elhajlása
(εa) az Ma forgatónyomatékkal,
a b) esetben a
ív elhajlása
(εa) az Ma forgatónyomatékkal,
a b) esetben a 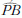 ív
(εb) elhajlása az Mb forgatónyomatékkal arányos.
Mondhatjuk, hogy az AA? szakasz hossza annyiszorosa
a BB? szakasz hosszának, ahányszorosa az Ma
nyomaték nagysága az Mb nagyságának.
ív
(εb) elhajlása az Mb forgatónyomatékkal arányos.
Mondhatjuk, hogy az AA? szakasz hossza annyiszorosa
a BB? szakasz hosszának, ahányszorosa az Ma
nyomaték nagysága az Mb nagyságának.
Vegyük észre azt is, hogy az AA? irány közelebb áll a függőlegeshez, mint a BB? irány! Egyszerű geometriai megfontolásból következik, hogy a végpontok lesüllyedésének aránya
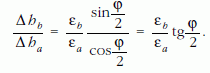
Másrészt
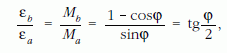
ezért
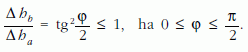
Beláttuk tehát, hogy a két fémszál egymásnak megfeleltetett pontjai közül (a végpontoktól eltekintve) mindig az a) esetbeli pontoknál fellépő deformáció ad nagyobb járulékot a szál végének lesüllyedéséhez. Mivel a teljes alakváltozás összetehető az egyes spirálrugók deformációiból származó alakváltozásokból, kimondhatjuk: az a) esetben nagyobb a szál végpontjának lesüllyedése.
Megjegyzések. 1. Energetikai megfontolásokkal és integrálszámítással numerikusan is meg tudjuk határozni a kétféle lesüllyedés arányát, jóllehet a versenyen ez nem volt feladat.
Ha a fogas végére – óvatosan növelve a terhelést – maximálisan G nagyságú erőt fejtünk ki, és ennek hatására a végpont Δh-val mélyebbre kerül, akkor összesen
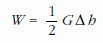
munkát végzünk. (Az 1/2-es faktor onnan származik, hogy az erő átlagértéke a maximális érték fele.) Ez a munkavégzés a kicsit meghajlított szálban tárolt rugalmas energiával egyenlő, ami a szál egyes darabkáiban tárolt energiák összegeként számítható. Egy-egy darabka rugalmas energiája – a megfeszített egyenes rugó energiaképletének analógiájára – a darabka hosszával és a végein ható forgatónyomaték négyzetével arányos. Ezek szerint a kétféle ruhafogas energiaviszonyait összevetve:
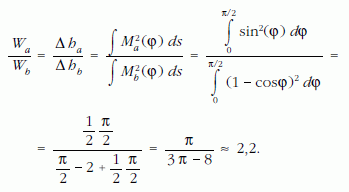
2. Természetesen más úton is eljuthatunk a helyes válaszhoz. Minden egyszerű megfontolás során a negyedkör alakú rugalmas fémszálat valamilyen egyszerű módon modellezzük. Az egymásnak megfeleltethető ívek, szakaszok deformációit hasonlítjuk össze, s ebből következtetünk a végpont lesüllyedésére. Tekinthetjük az eredeti negyedkörívek helyett akár a 9. ábrán látható derékszögeket is! Ebben a közelítésben a teljes alakváltozás két tag összegeként, a (kezdetben) vízszintes, illetve függőleges szárak deformációjából tehető össze.
A vízszintes szakaszok lehajlása, ha a függőleges szárak nem tudnának elmozdulni, azonos terhelés esetén ugyanakkora lenne; eddig tehát még egyformán viselkedik a két ruhafogas. A függőleges szakaszok deformációjának hatása a végpont lesüllyedésére azonban a két változatnál már különböző lesz. Az a) esetben a derékszög függőleges szára is elgörbül (hiszen a vízszintes szár a sarokpontnál forgatónyomatékot fejt ki rá), s ez az A? végpont további függőleges elmozdulását eredményezi. A b) esetben viszont a függőleges szár alakja gyakorlatilag változatlan marad, mindössze elfordul (a vízszintes szár lehajlása miatt); ez az elfordulás azonban a B végpont majdnem pontosan vízszintes irányú elmozdulását hozza létre, tehát nem járul hozzá annak függőleges irányú lesüllyedéséhez.
Látható, hogy ebben a durva modellben az a) esetbeli végpont lesüllyedése körülbelül kétszerese a b) esetbelinek, és sejthető, hogy az eredeti, negyedkörív alakú szálakhoz visszatérve a lehajlások arányának számértéke ugyan más lesz, de az egyenlőtlenség iránya nem változik meg.
Egyedi és igazán Károlyházyra jellemző ennél a feladatnál a probléma felvetése; a fizikai mondanivaló elbújtatása egy banális, hétköznapi, és éppen ezért izgató, azonnali választ követelő kérdés mögé. A 2. kiegészítés ad példát egy kvalitatív, mégis elfogadható válaszra.
Zárjuk ezt a visszatekintést azzal a 2005-ben feladott példával, amellyel Károlyházy Frigyes azt mutatta meg, hogy lehet még a sokat szidott állócsiga-mozgócsiga témakörben is új és érdekes problémát felvetni. A megoldás itt se lesz könnyű, fel kell gyűrni az ingujjat hozzá.
Két rögzített, egymástól l = 2 m távolságra levő csigán erős, de nem nyúlékony fonalat vezetünk át, és a végeire egy-egy M = 1 kg tömegű testet erősítünk a 10.a ábra szerint. (A fonal néhányszor 10 N terhelést bír ki szakadás nélkül. A csigák és a fonal tömege elhanyagolható.) Ha ujjunkkal lehúzzuk a fonal közepét úgy, hogy a két test 1-1 méterrel megemelkedjék (10.b ábra), majd elengedjük, a fonal elpattan, amikor A és B között "kiegyenesedik". Ha azonban úgy engedjük el, hogy előbb egy ugyancsak 1 kg tömegű testet erősítünk a fonal közepéhez, akkor a fonal a továbbiakban nem szakad el.
Megoldás. a) Azt kell észrevenni, hogy amikor a fonal kiegyenesedik, abban a pillanatban a fonalat két oldalról húzó testek már állnak. Rendkívül rövid idő alatt kell megállniuk, lefékeződniük arról a v = (2gh)1/2 ≈ 16 km/h sebességről, amire addigi mozgásuk (szabadesés) során felgyorsultak. (Itt és a továbbiakban h = 1/2l = 1 m.) Ha a fékezést "pillanatszerűnek" gondolnánk, vagyis a fékezés ideje Δt → 0 lenne, akkor a testek gyorsulása és a fonalat feszítő F erő is minden határon túl nőne, ezért elpattanna a fonal.
A valóságban természetesen még a "nem nyúlékony" fonal sem abszolút nyújthatatlan, hanem egy kicsit deformálható. Ehhez az alakváltozáshoz egy kicsiny, de véges Δt idő szükséges, így a testek gyorsulása és ezzel együtt a fonalat feszítő erő, ha nem is végtelenné, de nagyon naggyá válik. Mivel a fonal nem bír ki nagy erőt, elszakad.
b) Ábrázoljuk a folyamat három jellemző állapotát! A 11.a ábrán a kezdőállapotot tüntettük fel, megjelölve közben a középső test egyensúlyi helyzetét is, amelyen maximális sebességgel átlendül. A 11.b ábrán a fonal középső része vízszintes, a középső test azonban még emelkedik fölfelé. A 11.c ábra azt a pillanatot mutatja, amikor a középső test éppen megáll. Ekkor ismét állnak a szélső testek is. (Persze elképzelhető, hogy a középső test fel se emelkedik a 11.b ábrán látható helyzetig, ezt a lehetőséget majd számítással kell ellenőriznünk.)
A b) kérdés megfogalmazása arra utal, hogy a fonal ki fog egyenesedni, tehát a középső test eljut a 11.b ábrán jelzett állapotba. Lesz-e ott sebessége? Ezt érdemes kiszámítanunk. Írjuk fel a munkatételt a 11.a helyzettől a 11.b-ig jelzett folyamatra! A szélső testek h utat süllyednek, a középső h31/2 utat emelkedik, ezért
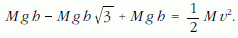
Felhasználtuk, hogy a 11.b helyzetben a szélső testek egy pillanatra megállnak, ezért csak a középső testnek lehet ekkor mozgási energiája. A felírt egyenletből a középső test sebessége:
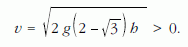
Tehát a középső test még valóban emelkedik. Meddig emelkedik? Ezt is kiszámíthatjuk, ha a 11.b és a 11.c állapotot energetikailag összehasonlítjuk:
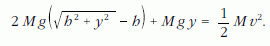
Ez y -ra nézve másodfokú egyenletté alakítható, amelynek megoldásai: y1 = -1,73h és y2 = 0,22h. (Az első gyök nyilván a kezdőállapotot adja meg, a 11.c állapotnak y2 felel meg.)
Hogy válaszolni tudjunk a feladat b) kérdésére, vizsgáljuk meg tüzetesen a 11.b ábrán látható helyzetet! Ebben a pillanatban a fonalat feszítő erő gyorsítja az éppen álló, de felfelé induló szélső testeket. Mekkora ez a gyorsulás? Tegyük fel, hogy a bal oldali csigától a középső testhez vezető AP fonál Δt idő alatt már egy kicsiny Δα szöggel túllendült a vízszintes helyzeten (12. ábra). Jelöljük a szélső testek sebességét Δv-vel! Ez a sebesség (a fonal nyújthatatlansága miatt) megegyezik a P pontban levő középső test sebességének AP irányú vetületével, vagyis
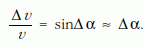
Másrészt a PQA derékszögű háromszögből
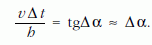
A fenti két egyenlet összevetéséből
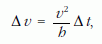
vagyis a szélső testek gyorsulására
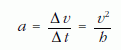
adódik.
Ugyanehhez a képlethez úgy is eljuthatunk, ha felírjuk, hogy a vízszinteshez közeli AP szakasz hossza időben hogyan változik. Mivel PQ ≈ v t (ahol t a 11.b ábrán látható állapottól mért idő), Pitagorasz tétele szerint
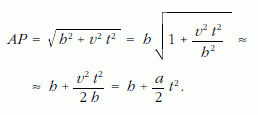
Ebből leolvashatjuk, hogy az AP szakasz hossza a = v2/h gyorsulással növekszik, és a fonal nyújthatatlansága miatt a bal oldali test is ugyanekkora nagyságú, függőlegesen felfelé irányuló gyorsulással kell, hogy rendelkezzék.
A fonal által kifejtett erő a szélső testek mozgásegyenletéből kapható meg:
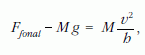
azaz
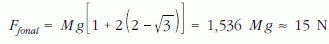
Így már érthető, miért nem szakad el ebben a helyzetben a "néhányszor 10 N terhelést kibíró" fonal.
Érdemes felfigyelni arra, hogy a szélső testek kétszer is emelkednek és kétszer is süllyednek egy-egy periódus során, hiszen a 11. ábrán feltüntetett mindhárom állapotban éppen állnak. Süllyedésük az idő függvényében nagyjából a 13. ábrán vázolt módon történik.
Radnai Gyula