Röntgen és nagysebességű elektronsugarak koherens szóródása atomokon. Az atomalakfaktor.

Röntgen és elektronsugarak szóródásának meg­határozására szolgáló elméleti számítások egyik legfontosabb tényezője az atomalakfaktor.

Röviden össze akarjuk foglalni azokat a mód­szereket, melyekkel eddig az atomalakfaktorokat meghatározták és rá akarunk mutatni arra, hogy hogyan lehet az eddig legpontosabbnak ismert atomalakfaktorokat, melyeket a »self consistent field« módszer segítségével meghatározott sűrű­ségre támaszkodva számítottak ki, olyan elemekre általánosítani, melyekre hasonló számítások még nem ismeretesek.

Az atomalakfaktort a szóró atom elektroneloszlása határozza meg. Ha ρ-val jelöljük a szóró atom vagy ion (továbbiakban atom) elektron­sűrűségét, akkor az atomalakfaktor, gömbszim­metrikus elektroneloszlást tételezve fel, a

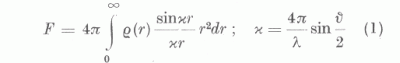
képlettel határozható meg. Így az atomalak­faktor meghatározására lényegében annyi mód­szert ismerünk, ahány módszer az atomok elektron­eloszlásának meghatározására ismeretes. λ a Rönt­gen-sugár hullámhossza és ν a szórási szög, r pedig az atommagtól mért távolság.

Atomok és ionok elektroneloszlásának meg­határozását a legkönnyebben a statisztikus atom­elmélet Thomas-Fermi módszerével végezhetjük el, mert az összes atomok és ionok elektroneloszlásá­nak meghatározása két a rendszámtól és az ioni­záció fokától független tabellázott függvényre vezethető vissza. Tekintve, hogy az atomalak­faktor értéke legjelentősebben az atom elektronjainak a maghoz közeleső részeken való eloszlásától függ és az atom belső részein a Thomas-Fermi módszerrel számított eloszlás igen jól átlagolja a valódi elektroneloszlást, így jó sikerrel használ­ható különösen nehezebb atomok esetében az atomalakfaktor meghatározására.

Bragg és West, Debye és Bewilogua számoltak a Thomas-Fermi módszerrel számított elektron­eloszlás alapján atomalakfaktorokat. A Thomas­-Fermi elméletben használatos x = r/µ, változót bevezetve (µ = 0,8853  a₀/Z^1/3) és a

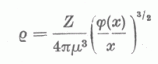
sűrűségeloszlást (1)-be helyettesítve nyerjük, hogy

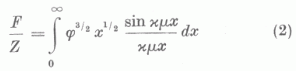
az u. n. redukált atomalakfaktor a

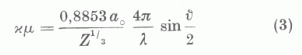
mennyiségnek a rendszámtól független függvényé. φ(x) a Thomas-Fermi egyenlet semleges atomokra ill. ionokra vonatkozó megoldása, a0 a legkisebb Bohr-féle elektronpályasugár a H-atomban. A módszer egyik igen nagy előnye, hogy az összes semleges atomok atomalakfaktorainak meghatá­rozása egy univerzális függvény meghatározására vezethető vissza, mivel φ₀(x), a Thomas-Fermi­-egyenlet semleges atomokra vonatkozó megoldása a rendszámtól független, univerzális függvény. Így semleges atomra a számítások könnyen keresz­tülvihetők.

Ionokra és semleges atomokra vonatkozólag is Szőkefalvy-Nagy végzett számításokat, mely­hez a Jensen által a statisztikus variációs mód­szerrel meghatározott elektroneloszlásokat hasz­nálta fel. Pauling és Shermann szintén számítottak atomalakfaktorokat; ők az atom sűrűségelosz­lását az egyes elektronok sajátfüggvényeinek segítségével építették fel, melyeket hidrogénszerűeknek választottak megfelelő árnyékolási állandókkal.

Az előzőknél lényegesen pontosabb elektron­eloszlások azok, melyeket a »self consistent field« módszerrel számítottak. Így ezen számításokkal egyidőben merült fel annak szükségessége, hogy az atomalakfaktorok meghatározását is ezen elektroneloszlások alapján végezzék el. Többek között James és Brindley voltak azok, akik az ide vonatkozó számításokat elvégezték s számításaik szerint, bár a statisztikus elektroneloszlás alapján számítottól általában nem túl nagy eltérés adódott, mégis az eltérés egyes helyeken az 5%-ot is eléri s így feltétlenül tekintetbe kell venni.

»Self consistent field« számítások azonban csak aránylag kevés elemre ismeretesek s így James és Brindley is szükségesnek találták, hogy egy inter­polációs eljárást dolgozzanak ki, mellyel oly atomok és ionok atomalakfaktorát is meghatá­rozhassák, melyekre a sűrűségeloszlás nem ismeretes.

Az interpolációs eljárás lényege a következő: egy atom teljes elektronsűrűsége az egyes elektro­nok sűrűségeinek összege. Ezt tekintetbe véve (1) szerint az atom alakfaktora is az egyes elektronok alakfaktorának összegeként állítható elő. Az egyes elektronok alakfaktorai azonban próbálgatással olyan koordinátarendszerbe transzformálhatók, ahol azok univerzális lefutást mutatnak s így a transzformáló paramétert interpolálva meg­kapható a kiválasztott elektron hozzájárulása a teljes atomalakfaktorhoz. Az eljárást minden elektronnal végrehajtva a teljes atomalakfaktor meghatározható. A módszernek egy igen lényeges hiányossága azonban az, hogy az interpoláció kellő biztonsággal csak akkor hajtható végre, ha olyan rendszámokat vizsgálunk, melyek kör­nyezetében több »self consistent field« módszerrel végzett számítás már ismeretes. Lényegesen kor­látozza az interpoláció alkalmazhatóságát az a tény, hogy kevés olyan elemre végeztek a »self consistent field« módszerrel számításokat, melyek­nél a nagyobb főkvantumszámú állapotok is be vannak töltve úgy, hogy ezeknek interpolációja bizonytalan.

Ezek után nyilvánvaló annak a szükségessége, hogy a »self consistent field« módszerrel számított atomalakfaktorok általánosítására, azok más rend­számú elemekre való transzformációjára, kon­zekvens eljárást dolgozzunk ki.

Legyen egy semleges Z rendszámú atom potenciálja

ahol Z_pe az atom effektív magtöltése természetesen még az r helykoordináta függvénye; e az elemi töltés. A Thomas-Fermi elmélet φ₀(x) függvénye igen szoros összefüggésben van Z_p-vel ugyanis, mint könnyen kimutatható

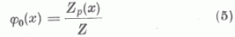
az u. n. redukált effektív magtöltést írja le, ha a helykoordinátát a Thomas-Fermi elmélet atomról-atomra változó µ = 0,8853 a_o/Z^1/3 egy­ségében mérjük. Mint a statisztikus atomelmélet­ből ismeretes φ_o/(x) az összes elemekre ugyanaz, tehát a rendszámtól független. Mint egy előző dolgozatában a szerző megmutatta Z_p/Z a hullám­mechanikai »self consistent field« módszer ki­cserélődés nélküli közelítésében is univerzálisnak tekinthető, ha az x koordinátát vezetjük be.

Felhasználva a gömbszimmetrikus sűrűség­eloszlásra vonatkozó

Poisson-egyenletet, parciális integrálások után a redukált atomalakfaktorra nyerjük

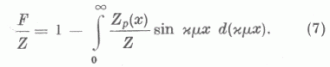
A (7) alak nyilvánvalóvá teszi, hogy a »self consistent field« módszerrel meghatározott atom­alakfaktorok is jó közelítéssel xµ, univerzális függvényének tekinthetők. Az 1. ábrán néhány elem redukált atomalakfaktorát mutatjuk be ebben az univerzális koordinátarendszerben. xµ kifejezését felhasználva az ismeretes atomalak­faktorokból transzformációval azon elemekre is nyerhetünk atomalakfaktorokat, melyekre a »self consistent field« módszerrel még nem végeztek számításokat. A transzformáció természetesen annál jobb eredményre vezet, minél kisebb a transz­formációban szereplő elemek rendszámai között a különbség. Szembetűnő az ábrán, hogy az atomalakfaktorok oly egymástól távol fekvő elemek esetében, mint a Hg és Ar is nagymértékben meg­egyeznek. A Zn atomnál a külső részeken tapasz­talható aránylag nagyobb eltérés az Ar és Cl atomok atomalakfaktoraitól az elektronszerkezet­beli különbségre vezethető vissza. Az előbbi lezárt d héjjal, míg az utóbbiak lezárt ill. egy elektron hiánnyal rendelkező (s, p) héjjal rendel­keznek. A Zn atom alakfaktorához hasonló visel­kedés nyomai a Hg-nál is kimutathatók. A transz­formációnál az itt említett sajátságok is .figyelembe vehetők. Végül említsük meg, hogy az 1. ábrán látható függvények analitikus alakkal is közelíthetők s így pl. az (s, p) lezárt héjjal vagy ehhez hasonló elektronszerkezettel rendelkező atomok atomalak­faktorai számára a

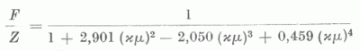
formula adható meg, mely a számítottól maximá­lisan 2%-al tér el.

A transzformáció ionok atomalakfaktorának meghatározására is felhasználható, itt csupán egy kissé bonyolultabb feladat előtt állunk, mert a transzformáció nem az azonos töltésű ionok között hajtható végre, hanem az azonos ioni­zációsfokú ionok-tehát melyekre a q = (Z -N)/Z mennyiség egyezik meg - atomalakfaktorai hozhatók egymással kapcsolatba.

Gáspár Rezső
Műszaki Egyetem Fizikai Intézete, Budapest