Finomszerkezet vizsgálat röntgensugarakkal I.

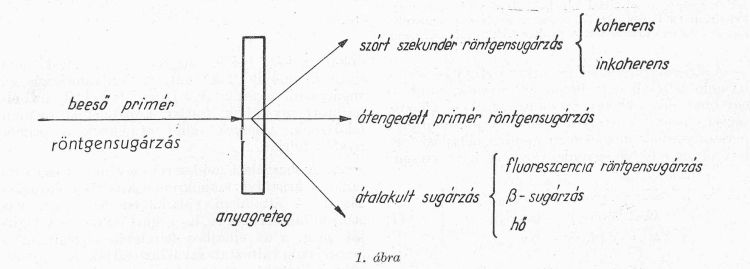
Ha röntgensugárzás anyagrétegbe ütközik, akkor egy része irány és hullámhossz változás nélkül átmegy az anyagon, egy része szóródik az anyag atomjainak elektronburkán, egy része pedig másfajta sugárzások gerjesztésére fordítódik. A primér röntgensugárzás energiájának megoszlását vázlatosan az alábbi ábra szemlélteti:

Mivel a felsorolt effektusok a röntgensugárzás és az anyagréteg kölcsönhatásának eredményei, várható, hogy az effektusokból következtetni lehet az anyagréteg sajátságaira. Elméleti szempontból mindegyik effektus vizsgálata fontos, a gyakorlati anyagvizsgálatban azonban főleg háromnak van különös jelentősége:

1. Durvaszerkezet vizsgálatnál az átengedett primér nyalábot, pontosabban az anyagrétegnek a primér nyaláb által vetett árnyképét vizsgálják, s az árnykép részeinek különböző fedettségéből az anyag belső egyenetlenségeire és hibáira (idegen zárványok, üregek, repedések stb.) következtetnek (röntgen hibakeresés - defektoszkópia).

2. Röntgen spektroszkópiánál az anyagrétegben gerjesztett fluoreszcencia röntgensugárzás spektrumát tanulmányozzák, és a spektrumvonalak hullámhosszából és intenzitásából a gerjesztett atomok minőségét és százalék arányát határozzák meg (kvalitatív és kvantitatív röntgen kémiai analízis).

3. Végül a finomszerkezet vizsgálat tárgya az atomok elektronburkain szóródó szekundér röntgensugárzás, illetve annak a primér sugárzással azonos hullámhosszú koherens része. A koherens szórt sugárzáson kívül a Compton-effektus eredményeképpen fellép még egy inkoherens szórt sugárzás is, amelynek hullámhossza nagyobb a primér sugárzásénál.

Koherens szórás elvileg minden irányban van. Ha azonban a szórócentrumok rendezetten helyezkednek el, akkor a szórt hullámok interferencia révén bizonyos irányokban erősítik, más irányokban gyengítik egymást, s így szórt sugárzás csak egyes diszkrét irányokban lesz észlelhető. Ez a helyzet pl. a kristályoknál, ahol az atomok párhuzamos irányokban azonos távolságokra következnek egymásután, vagyis - optikai analógiával élve - háromdimenziós rácsot alkotnak. Ha tehát egy kristályt röntgensugarakkal világítunk át, akkor a kristály mögött elhelyezett fényérzékeny filmen diszkrét foltokból álló elhajlási kép jelenik meg (l. 2. ábra).

A kristályrácsoknál jelentkező elhajlási képre hasonló feltételi egyenletek érvényesek, mint az egydimenziós optikai rácsokra azzal a különbséggel, hogy kristályrácsoknál a háromirányú periodicitásnak megfelelően minden elhajlási folthoz három feltételi egyenlet tartozik, nevezetesen:

Az egyenletekben szereplő betűk jelentése: h, k, l tetszés szerinti egész számok (az elhajlási folt rendszámai), λ a röntgensugárzás hullámhossza, a, b, c, a három dimenziónak megfelelő három rácsállandó, végül a hat szögfüggvény a beeső, ill. az elhajlított nyaláb iránycosinusai. Mivel mind a beeső, mind az elhajlított nyaláb iránycosinusainak négyzetösszege 1-gyel egyenlő, fenti három feltételi egyenlethez (ún. Laue-egyenletek) még két további egyenlet járul. Az egydimenziós optikai ráccsal ellentétben ennek az egyenletrendszernek adott λ és adott beesési szög esetén nincs mindig megoldása, ami azt jelenti, hogy ha nyugvó kristályt monokromatikus röntgennyalábbal megvilágítunk, nem mindig kapunk elhajlási képet. Ezt a nehézséget a gyakorlatban háromféleképpen lehet kiküszöbölni: 1. Az ún. Laue-módszernél a nyugvó kristályt folytonos röntgensugárzással világítják meg, amelyben mindig vannak a feltételi egyenleteket kielégítő hullámhosszak. Ennek a módszernek az az előnye, hogy a kristály felvétel közben nyugszik, így az elhajlási képből a kristály térbeli orientációjára, megfelelő beállítás esetén pedig a kristály szimmetriájára is következtethetünk (l. 3. ábra). Hátránya viszont, hogy a rácsállandókat nehéz belőle meghatározni, mert nem tudjuk, melyik folt milyen hullámhosszúságú sugárzástól származik. Laue-felvételnél az elhajlított nyalábok foltjai kúpszeletek mentén feküsznek, amelyek mind átmennek a primér nyaláb foltján.

2. A vizsgálati módszerek egy másik csoportjánál a kristályt monokromatikus röntgensugárzással - általában valamilyen fém (réz, vas stb.) karakterisztikus K_α sugárzásával - világítják meg, s az elhajlási feltételek kielégítését a beesési szög változtatásával biztosítják. Legegyszerűbb változata az ún. forgó kristályos módszer, amelynél a kristályt egy tengely körül forgatják, és az elhajlási képet a kristály köré terített nyugvó hengeres filmre veszik fel. Forgókristályos felvételeken az elhajlított nyalábok foltjai párhuzamos vonalak (az ún. rétegvonalak) mentén helyezkednek el. (l. 4. ábra)

A módszer újabb változatainál a kristály forgatásával egyidőben a filmet is mozgatják, ezáltal az elhajlási képet alkalmas módon széthúzzák, ami jelentősen megkönnyíti a foltok identifikálását és a rácsállandók meghatározását. A mozgófilmes eljárások egyik korszerű változatánál, a Weissenberg-módszernél, az elhajlított nyalábok foltjai parabolákra emlékeztető asszimmetrikus görbék mentén feküsznek (l. 5. ábra), a legújabban bevezetett de Jong-Bouman-módszernél pedig jól áttekinthető kétdimenziós hálózatot alkotnak (l. 6. ábra), amelyből a kristály rácsállandói viszonylag egyszerűen meghatározhatók.

3. Végül a Debye-Scherrer-módszernél a kristályt finom porrá törik, a porból kis abszorpciójú amorf kötőanyaggal hengert formálnak, s azt monokromatikus röntgensugárzással világítják át. Mivel a hengeres anyagminta parányi kristálykék (ún. krisztallitok) rendezetlen halmaza, amelyben minden lehetséges kristályorientáció előfordul, a röntgensugarak elhajlása szempontjából a porhenger egy minden lehetséges tengely körül körbenforgatott egykristálynak felel meg. A feltételi egyenletek kielégítését tehát tulajdonképpen a Debye-Scherrer-módszernél is a beesési szög változtatásával biztosítják. Az elhajlított nyalábok egyébként ennél a módszernél ívalakú foltokat, ún. Debye-Scherrer-gyűrűket adnak (l. 7. ábra). A gyűrűk minden pontja más-más krisztallittól származik, a gyűrűk a sok apró elhajlási kép összeolvadásából jönnek létre.

Az előző paragrafusban mondottakból következik, hogy minden röntgen finomszerkezet vizsgáló készülék elvileg három részből áll: 1. a röntgensugarakat előállító sugárforrásból, 2. az anyagminta beállítására és mozgatására szolgáló goniométerből, és végül 3. az elhajlított nyalábokat regisztráló készülékből. Vegyük sorra az egyes részeket.

1. A sugárforrás. A Laue-módszerhez 50-60kV anódfeszültséggel táplált wolfram-antikatódos röntgencső fékezési sugárzását, a többi módszerhez pedig 30-40kV feszültséggel táplált réz, vas stb. antikatódos röntgencső karakterisztikus K_α sugárzását használják. A röntgencsövek hatásfoka igen rossz, a betáplált energiának csak igen kis hányada fordítódik röntgensugárzás gerjesztésére, a legnagyobb része hővé alakul át. Pl. egy 40kV anódfeszültséggel és 10mA anódárammal működtetett réz-antikatódos röntgenesőnél a betáplált 400W teljesítménynek kb. 99,84%-a, vagyis gyakorlatilag majdnem az egész hőtermelésre, az antikatód melegítésére fordítódik, és csak a fennmaradó 0,16% fordítódik röntgensugárzás gerjesztésére. Ezért az antikatódot a gyakorlatban üregesre készítik, és víz átáramoltatásával hűtik.

2. Finomszerkezet vizsgálatokhoz az anyag szóróképességétől függően néhány tized mm átmérőjű anyagminták kellenek. Az anyagmintát tartó goniométer úgy van kiképezve (l. 8. ábra), hogy az anyagmintát három egymásra merőleges eltolás, azonkívül három egymásra merőleges tengely körüli forgatás révén tetszés szerinti helyzetbe be lehessen állítani. A goniométerhez a legtöbb vizsgálati módszernél még valamilyen mozgatóberendezés is csatlakozik, fotografikus regisztrálásnál azonkívül az egész egybe van építve a fényérzékeny filmet tartó kamrával (l. 9. és 10. ábra).

3. Az elhajlított nyalábok regisztrálása a használatban levő készülékek legnagyobb részénél fotografikus úton, fényérzékeny film segítségével történik. Ezenkívül úgyszólván a vizsgálatok megindulása óta használnak regisztráló készüléknek atmoszféra nyomású argonnal töltött ionizációs kamrákat, újabban pedig G. M.-csöveket is. Az ionizációs kamrák és a G. M.-csövek nagy előnye, hogy velük az elhajlított nyalábok intenzitása közvetlenül meghatározható, míg a fotográfiai módszernél a foltok feketedéséből külön méréssel kell az intenzitásokat megállapítani. Az automatikus regisztrálásra berendezett korszerű G. M.-csöves finomszerkezet vizsgáló készülékek (l. 11. és 12. ábra) teljesítőképessége sok, ipari szempontból fontos vizsgálatnál (keverékanalízis, kitüntetett orientációk vizsgálata stb.) messze meghaladja a fotografikus regisztrálással dolgozó készülékek teljesítőképességét, ezért a viszonylag magasabb beszerzési költség ellenére alkalmazásuk rohamosan terjed. Végül érdemes megemlíteni, hogy újabban történtek kísérletek az elhajlított nyaláboknak elektronsokszorozóval, szcintilláló kristályokkal, valamint fotokonduktív félvezető kristályokkal történő regisztrálására, sőt próbálkoznak az elhajlítási képnek televíziós képcső útján történő felerősítésével és kivetítésével is. Ezek az eljárások azonban még kísérleti stádiumban vannak, úgyhogy használhatóságukról korai volna jóslásokba bocsátkozni.

Láttuk, hogy a röntgensugarak szóródása csak akkor ad diszkrét foltokból álló elhajlási képet, ha az átvilágított anyagban a szórócentrumok (atomok) rendezetten oszlanak el, vagyis ha az anyagminta kristályos szerkezetű. Kérdés mármost, hogy ez a megkötöttség nem korlátozza-e túlságosan szűk területre a röntgen finomszerkezet vizsgálat alkalmazási lehetőségeit. Az elmúlt évtizedek tapasztalatai azt mutatták, hogy komolyabb korlátozásoktól több okból nem kell tartani.

Először is a kristályokra jellemző rendezett felépítés nem kivétel számba menő ritkaság, hanem a szilárd fázis természetes megjelenési formája. A szilárd anyagok túlnyomó többségénél azonban (pl. a különböző fémkészítményeknél) a kristályrácsra jellemző háromirányú periodicitás gyakran csak szubmikroszkopikus méretű tartományokra, ún. krisztallitokra korlátozódik, melyek statisztikus rendezetlenségben helyezkednek el egymáshoz képest. Az ilyen, ún. polikristályos anyagok (pl. rézdrótok) kész Debye-Scherrer-anyagminták, amelyek monokromatikus röntgensugárzással megvilágítva a már ismertetett "gyűrűs" elhajlási képet adják. A semmiféle rendezettséget nem mutató amorf anyagok a természetben igen ritkák (üvegek, gyanták stb.), a; korábban amorfnak tartott anyagok jórészéről a vizsgálati eljárások finomodásával kiderült, hogy parányi krisztallitok rendezetlen halmazából állnak. A kristályos és amorf anyagok között tehát nincs éles szakadék, csak folytonos átmenet (vö. 15. és 18. ábra).

Másodszor: a teljes háromirányú periodicitást mutató kristályos anyagokon kívül (különösen a nagymolekulájú szerves anyagok körében) találunk kétirányú periodicitást mutató réteges, ill. hártyás, valamint egyirányú periodicitást mutató rostos szerkezetű anyagokat is. Ezeknél a rétegeken, ill. rostokon belül az atomelrendezés periodikus, az egyes rétegek, ill. rostok távolsága és orientációja azonban változó. Mivel az elhajlási kép létrejöttéhez már egyirányú periodicitás is elegendő, a finomszerkezet vizsgálat számára ezek az anyagok is hozzáférhetők.

Végül az elhajlási kép keletkezésének alapfeltétele, a szórócentrumok rendezett elhelyezkedése, primitívebb formában ugyan, de megtalálható a többatomos gázoknál és folyadékoknál is. Nézzük először a gázokat. Bár az egyes gázmolekulák nagy sebességgel változtatják helyüket, és statisztikusan oszlanak el a gáztérben, a molekulákon belül az atomok kölcsönös helyzete minden molekulánál ugyanaz, s ez a "belső periodicitás" a Debye-Scherrer-gyűrűkre emlékeztető, csak éles vonalak helyett széles sávokból álló elhajlási képet hoz létre (l. 13. ábra). Folyadékoknál annyival bonyolultabb a helyzet, hogy ott a gázokra jellemző belső periodicitáson kívül fellép egy "külső periodicitás" is. A folyadékmolekulák szoros illeszkedése folytán ugyanis a szomszédos molekulák száma és átlagos távolsága időben változatlan, amiből szintén kiadódik egy elhajlási jelenség, s ez a kép szuperponálódik a belső periodicitásból adódó elhajlási képre (l. 14. ábra). Hasonló a helyzet az amorf szilárd anyagoknál is, úgyhogy a röntgen finomszerkezet vizsgálati módszerek ezekre is kiterjeszthetők (l. 15. ábra).

Röntgen finomszerkezet vizsgálati módszerekkel tehát gyakorlatilag minden anyag tanulmányozható. Az univerzális alkalmazhatóság mellett a finomszerkezet vizsgálat további nagy előnyei: a vizsgálatokhoz igen kevés anyag kell (szükség esetén már 1mg anyag is elegendő), a vizsgálat az anyagmintát nem roncsolja, végül a vizsgálat eredményét reprezentáló felvétel, ill. diagramm megőrizhető, s a kiértékelés bármikor ellenőrizhető.

A különböző anyagoknál azonos körülmények között észlelhető elhajlási jelenségek az elhajlított nyalábok száma, iránya, keresztmetszete és intenzitása szempontjából különböznek egymástól. A finomszerkezet vizsgálatnak mármost kettős feladata van:

1. az elhajlási jelenség jellemző adatainak minél pontosabb kvantitatív meghatározása (mérés),

2. az elhajlási kép jellemző adataiból a vizsgált anyagminta sajátságainak megállapítása (kiértékelés).

Az egyes adatok mérése a regisztrálás módjától függően különbözőképpen történik. Automatikus regisztrálásra berendezett G.M.-csöves készülékeknél pl. az elhajlított nyalábok iránya és intenzitása a diagrammról közvetlenül leolvasható, ezzel szemben fotografikus észlelésnél az elhajlított nyalábok irányát a foltok helykoordinátáiból számítással, intenzitását pedig a foltok feketedéséből denzitométeres méréssel kell meghatározni. A következőkben a különféle kiértékelési módok ismertetésénél az egységesség kedvéért a nehézkesebb, de ez idő szerint még általánosabban elterjedt fotografikus regisztrálást vesszük alapul, megállapításaink azonban könnyen átvihetők akármilyen más regisztrálási módra is. Vegyük ezekután sorra, miféle információk nyerhetők egy elhajlási képből.

A finomszerkezet vizsgálat egyik igen fontos gyakorlati alkalmazásának alapja az a tapasztalat, hogy a különféle anyagokról készített Debye-Scherrer-felvételeken a vonalak száma, helye és feketedése (vagyis az elhajlított nyalábok iránya is intenzitása) ugyanúgy jellemző az anyagra, mint az emberre az ujjlenyomat. Egy kellő számú adatot tartalmazó, megfelelően rendezett Debye-Scherrer-felvétel gyűjtemény birtokában tehát egyszerű összehasonlítással identifikálható minden olyan anyag, amelynek elhajlási képe a gyűjteményben már szerepel. Azonkívül mivel keverékeknél az alkotóelemek elhajlási képei szuperponálódnak, e módszer segítségével keverékek összetétele, sőt a vonalak intenzitás viszonyaiból a komponensek százalékaránya is meghatározható.

A Debye-Scherrer-felvételek alapján történő identifikálást sokan a kémiai analízis egyik ágának tekintik, jóllehet egészen másról van szó. Az elhajlási kép alapján történő identifikálás független az anyag kémiai összetételének ismeretétől, s ennek megfelelően egyrészt olyan anyagok azonosítására is felhasználható, amelyeknek kémiai összetétele nem ismeretes, másrészt különbséget lehet vele tenni azonos kémiai összetételű, de különböző atomelrendezésű, s ennek megfelelően különböző fizikai sajátságokkal rendelkező ún. polimorf anyagok (pl. grafit, gyémánt, amorf szén; fémek különböző módosulatai stb. között).

Az identifikálási módszer ez idő szerint főleg szervetlen anyagok vizsgálatánál játszik fontos szerepet, itt ugyanis már rendelkezésre áll egy több mint 5000 szervetlen anyag adatait tartalmazó s állandóan bővülő adatgyűjtemény (ASTM index), amellyel a gyakorlatban előforduló keverék analízisek többsége megoldható. A röntgen analízist a különböző kémiai iparok mellett főleg a tűzálló anyag iparban (a Si0₂ három kristályos módosulatának: a kvarcnak, tridimitnek és krisztobalitnak kimutatására), a fémiparban (ötvözetek analízisére) és a bányászatban (hasznos ásványok és ércek összetételének megállapítására) használják (l. 16. ábra), 2. Krisztallit és szemcsenagyság meghatározás Említettük már, hogy a szilárd anyagok többsége polikristályos felépítésű, vagyis parányi kristálykák, úgynevezett krisztallitok, rendezetlen halmazából áll. A krisztallitok nagysága szoras kapcsolatban van az anyag mechanikai sajátságaival, ezért a gyakorlati alkalmazások szempontjából fontos feladat a krisztallitok méretének meghatározása. Ennek egyik módja azon a tapasztalaton alapul, hogy a polikristályos anyagokról készült Debye-Scherrer-felvételek .gyűrű.-inek jellege (egyenletessége, szélessége) függ a krisztallitok méretétől. Mégpedig a Debye-Scherrer-felvételek gyűrűiből kétféleképpen lehet a krisztallitok méretét megbecsülni.

Ha a krisztallitok átmérője 10^-4cm-nél nagyobb, akkor a Debye-Scherrer-gyűrűk apró foltokra, pettyekre esnek szét, melyek nagyságából a krisztallitok mérete meghatározható (l. 17. ábra).

Ha viszont a krisztallitok átmérője 10^-5cm-nél kisebb, akkor a gyűrűk kiszélesednek (l. 18. ábra), s ilyenkor a kiszélesedés mértékéből lehet következtetni a krisztallitok méretére. Utóbbi módszer elvi alapja az az optikából ismert tapasztalat, hogy optikai rácsnál az elhajlító rések (vagyis röntgensugárzásnál az elhajlító atomok) számának csökkenésével az elhajlási kép egyre jobban elmosódik, a vonalak egyre szélesebbek lesznek (l. 19. ábra). A vonalszélesedésből történő krisztallitméret meghatározást némileg bonyolítja az a körülmény, hogy a vonalak kiszélesedésének oka nemcsak a kis krisztallit méret lehet, hanem a kristályrács deformációja, disztorziója is. A disztorzió folytán ugyanis az egyes krisztallitok rácsállandói szűk határok között ingadoznak, s természetesen velük együtt ingadoznak az (1) egyenleteket kielégítő szögek is. Ez az eset különösen hidegen megmunkált fémkészítményeknél gyakori, ezért itt a vonalszélesedés interpretálásánál óvatosan kell eljárni.

A krisztallitok méretének ismeretén kívül finom eloszlású anyagoknál (porok, kolloidok) gyakran igen fontos az egyes anyagrészecskék, szemcsék nagyságának ismerete is. A szemcsék mindig nagyobbak mint a krisztallitok, egy-egy szemcse általában több különböző orientációjú s egymással mereven összekapcsolt krisztallitból áll (l. 20. ábra). A szemcsenagyság gyakorlati jelentősége abban van, hogy adott anyagmennyiségnek annál nagyobb felület felel meg, minél apróbb szemcsékből áll, tehát az anyag összes felülettől függő sajátságai (kémiai reakció képesség, katalizátor hatás, adszorpció, tapadó képesség stb.) szoros kapcsolatban vannak a szemcsemérettel. Finom eloszlású polikristályos anyagok Debye-Scherrer-diagrammjából a szemcsenagyság is meghatározható, mégpedig a szemcsék méretére a primér nyaláb közvetlen közelében haladó elhajlított nyaláb kiszélesedéséből, az ún. kisszögű szórásból lehet következtetni (l. 21. ábra). A kisszögű szórásnál ugyanis az egy szemcsén belül levő különböző orientációjú krisztallitok atomjai a merev kapcsolat folytán azonos fázisban szórnak, így az egész szemcse egyetlen krisztallitként viselkedik. A kisszögű szórás vizsgálata fejlett kísérleti technikát igényel: az elhajlított nyalábnak a közvetlen közelében haladó igen intenzív primér nyalábtól való elválasztásához jól fókuszált monokromatikus röntgensugárzás, igen hosszú kamra és a levegő abszorpciójának kiküszöbölése céljából jó vákuum kell. A kisszögű szórást a gyakorlatban főleg kolloid részecskék nagyságának meghatározására használják.

Polikristályos fémkészítményekben hideg megmunkálás (hengerlés, húzás stb.) hatására általában kitüntetett orientáció lép fel, ami azt jelenti, hogy az eredetileg statisztikus rendezetlenségben elhelyezkedő krisztallitok fokozatosan beállnak bizonyos irányokba. Mivel a jelenség nagyon hasonlít a természetes és mesterséges rostok (gyapot, gyapjú, műselyem stb.) hosszú molekuláinak rendezett beállásához, kitüntetett orientáció helyett szokás rostos szerkezetről, textúráról is beszélni. Az orientálódás foka szoros kapcsolatban van az anyag mechanikai sajátságaival, pl. drótoknál és textilrostoknál a szakítási szilárdság, lemezeknél a formálhatóság, transzformátor-lemezeknél a vasveszteség stb. az orientálódás mértékének függvénye, ezért van a kitüntetett orientációk vizsgálatának ipari jelentősége. Az ipari alkalmazásokon kívül fontos szerepe van a kitüntetett orientáció vizsgálatának a geológiában is, mert a kőzetek kitüntetett orientációjából következtetni lehet rá, hogy keletkezésük idején a földkéregben milyen irányú erők hatottak, milyen feszültségek működtek.

A krisztallitok kitüntetett orientációjára, ill. a rostszerkezetre legcélszerűbben a polikristályos anyag Debye-Scherrer diagrammjából következtethetünk. A Debye-Scherrer-gyűrűk ugyanis az egyes krisztallitok elhajlási képének összeolvadásából keletkeznek, így rendezetlen felépítésű polikristályos anyagoknál, ahol minden krisztallit orientáció egyenlően valószínű, a gyűrűk homogének, vagyis a feketedés a gyűrűk mentén köröskörül azonos. Ezzel szemben kitüntetett orientáció esetén bizonyos irányítású krisztallitok száma erősen megnő, s ezzel együtt a Debye-Scherrer-gyűrűk megfelelő szakaszain a feketedés erősen fokozódik, vagyis az eredetileg homogén gyűrű sötétebb és világosabb szakaszokra hasad szét (l. 22. és. 23. ábra). A sötétebb szakaszok helyéből a kitüntetett orientáció irányát, a feketedésből pedig az orientálódás mértékét lehet meghatározni.

Az egydimenziós optikai rács felépítésében mutatkozó szabályszerűség egyetlen adattal, a rácsállandóval jellemezhető. Ezzel szemben háromdimenziós kristályrácsoknál az alkotóelemek (atomok) szabályos ismétlődésének kvantitatív leírásához hat adat szükséges: a három dimenziónak megfelelő három rácsállandó és az általuk bezárt három szög (a három legkisebb ismétlődési távolságnak megfelelő három rácsállandó ugyanis nem mindig merőleges egymásra). Míg tehát az optikai rácsnál a jellegzetes ismétlődő elem egy egydimenziós tartomány, addig a kristályrácsok ismétlődő eleme egy háromdimenziós alakzat, egy általános parallelepipedon, amelynek egy csúcsban összefutó három éle a három rácsállandó. Ezt a parallelepipedont elemi cellának nevezik (l. 24. és 25. ábra). Az elemi cella háromirányú periodikus ismétléséből fel lehet építeni az egész kristályrácsot.

Ha egy ismeretlen rácsállandójú optikai rácsot monokromatikus fénnyel világítunk meg, akkor a fény hullámhosszából és az elhajlási kép geometriai adataiból az ismeretlen rácsállandó egyértelműen meghatározható. Hasonló a helyzet kristályrácsoknál is, azzal a különbséggel, hogy a változók nagyobb száma és a bonyolultabb elhajlási kép miatt kristályrácsoknál az eljárás jóval hosszadalmasabb. A kiértékelésnek azonban semmi elvi akadálya nincs, az elemi cella metrikus adatai az elhajlási képből mindig egyértelműen meghatározhatók, sőt az elhajlási kép geometriájából sok esetben következtetni lehet a kristályrács szimmetriaviszonyaira, vagyis a kristályrácsot önmagával fedésbe vivő szimmetriaműveletek összességére, az ún. tércsoportra is. (A tércsoport elnevezés arra utal, hogy a szimmetriaműveletek összessége matematikai értelemben csoportot alkot.)

Mivel a kristályok rácsállandói igen pontosan mérhetők (max 0,001%-os pontosság érhető el), azonkívül a mérések elvégzéséhez igen kevés anyag kell (szükség esetén 1-2mg már elegendő), a kristályrács méreteivel kapcsolatos több anyagi állandót gyakran előnyösebben lehet a röntgen elhajlási képből meghatározni, mint egyéb fizikai módszerekkel. A következőkben mutatunk erre néhány példát.

Az elhajlási képből történő sűrűség meghatározás gondolatmenete a következő. Az elemi cellában levő atomok atomsúlyának összege osztva a Loschmidt-számmal megadja az elemi cella tömegét, az elemi cella éleiből (rácsállandók) és szögeiből pedig ki lehet számítani az elemi cella térfogatát. A két adat hányadosa viszont nyilván egyenlő az elemi cella, és vele együtt az egész kristály sűrűségével. Az elhajlási képből történő sűrűségmérés a gyakorlatban főleg olyan esetekben fontos, amikor a vizsgálandó anyagból igen csekély mennyiség áll rendelkezésre, vagy az anyag fizikai állapota (likacsos anyagok, porok), ill. a mérési feltételek természete (pl. magas hőmérséklet) folytán más módszerek alkalmazása igen nehézkes volna.

b) A t o m-    é s    m o l e k u l a s ú l y    m e g h a t á r o z á s

Az előző pontban ismertetett gondolatmenet alapján nemcsak a sűrűséget lehet kiszámítani az atomsúlyokból és az elemi cella geometriai adataiból, hanem fordítva, a sűrűség ismeretében meg lehet határozni az atom-, ill. molekulasúlyokat is. Ha igen pontos sűrűségadatok állnak rendelkezésre, akkor az így számított atomsúlyok pontossága vetekszik a más eljárásokból adódó értékekkel, különösen olyan elemeknél, ahol a kémiai módszerek alkalmazása nehézkes (Mg, Al, Sn, Bi stb.). A fluor atomsúlyát pl. legpontosabban röntgen elhajlási képből határozták meg.

Fontos szerepe van a módszernek nagymolekulájú szerves anyagok molekulasúlyának meghatározásánál is. A szerves anyagok kristályrácsában a szerkezeti egység nem az atom, mint a szervetlen vegyületek nagy részénél, hanem a molekula. Tehát az elemi cella is molekulákból épül fel, amelyek száma az elemi cella méreteiből és szimmetriaviszonyaiból (tércsoport) vagy egyértelműen meghatározható, vagy legalább is jól becsülhető. Ezekből az adatokból viszont a sűrűség ismeretében a molekulasúly kiszámítható.

Ha egy kristályos anyag sűrűségét és alkotóelemeinek atomsúlyát ismerjük, akkor az elemi cella méreteiből az előzőkben vázolt gondolatmenet alapján a Loschmidt-szám kiszámítható. A Loschmidt-szám meghatározásának ez idő szerint ez a legpontosabb módszere, az irodalomban használatos Loschmidt-szám értéket öt kristályos anyag (NaCl, gyémánt, kalcit, LiF, KCl) elemi cella méreteinek és sűrűségének nagy pontossággal meghatározott adataiból átlagolták.

Mivel a hőmérsékletváltozásoknál észlelhető makroszkopikus térfogatváltozás lényegében az elemi cella méretváltozásának az eredménye, a különböző hőmérsékleten mért rácsállandókból a vizsgált anyag hőtágulási együtthatója meghatározható (l. 26. ábra). A módszer gyakorlati előnyeit illetően szóról szóra érvényesek a sűrűségmérésnél mondottak azzal a kiegészítéssel, hogy a röntgenvizsgálatokhoz szükséges kicsi anyagmintát jóval egyszerűbb konstans hőmérsékleten tartani, mint az egyéb mérő módszerekhez szükséges nagyobb anyagdarabokat.

Ha egy polikristályos anyagban belső feszültségek vannak, akkor a krisztallitok deformálódnak, vagyis elemi celláik méretei megváltoznak, s ennek megfelelően az elhajlási képben a vonalak eltolódnak. Az észlelt eltolódásokból a deformáció mértéke, ebből pedig az anyag rugalmas állandóinak ismeretében a megfelelő feszültségek meghatározhatók.

A módszer nagy előnye az egyéb feszültségmérési eljárásokkal szemben, hogy nem az összes deformációt, hanem csupán a rugalmas deformációt méri (a plasztikus deformáció ugyanis a kristály rácsállandóit nem változtatja meg), azonkívül lehetővé teszi a belső feszültség lokális változásának tanulmányozását egészen kis tartományokon belül. Hátránya viszont, hogy az anyagminta nagy abszorpciója miatt csak egy vékony felületi réteg viszonyairól tudósít, azonkívül igen fejlett vizsgálati technikát igényel, és csak olyan anyagoknál használható, amelyek elég éles elhajlási képet adnak. Nehezíti a vizsgálatot az a körülmény is, hogy az adatok kiértékeléséhez szükséges rugalmassági modulusz irányfüggő, így a számításokhoz nem lehet egyszerűen a makroszkopikus anyagmintára érvényes rugalmassági moduluszt használni.

Végül megjegyzendő, hogy a belső feszültség mérésének említett módszere csak olyan esetekben használható, amikor a feszültség homogén, vagyis a primér röntgennyaláb által átvilágított tartományban a krisztallitok azonos deformációt szenvednek. Ha ugyanis a deformáció iránya és mértéke krisztallitról krisztallitra változik, akkor az egyes krisztallitok elhajlási képében jelentkező eltolódások szuperpozíciója végeredményben nem vonaleltolódást, hanem vonalkiszélesedést eredményez. A vonalak kiszélesedéséből szintén következtetni lehet a belső feszültség mértékére, azonban a kiértékelésnél igen óvatosan kell eljárni, mert a vonalkiszélesedés oka nemcsak a belső feszültség lehet, hanem - mint már említettük - a kis szemcseméret is, sőt vonalszélesedésre vezethetnek bizonyos fajta rácshibák is. Az egyes effektusok szétválasztása a gyakorlatban nem könnyű, s elvileg azon alapul, hogy a különböző effektusok által okozott szélesedések különbözőképpen változnak az elhajlási szöggel.

Keverékkristályoknak az olyan kristályokat nevezzük, amelyeknél az ekvivalens (vagyis az egymástól egészszámú periódusra levő) rácspontokat két vagy több kristályfajta atomjai, ill. molekulái töltik be statisztikus rendezetlenségben. A keverékkristályok különösen fémeknél gyakoriak, ahol ötvözeteknek vagy szilárd oldatoknak hívják őket. Mivel a keverékkristály elemi cellájának rácsállandói a keverési arány függvényei, az elemi cella méreteiből az összetevők aránya meghatározható. (l. a 16. ábrán az első három felvételt, ahol az ezüstrácsba statisztikusan beépülő kadmiumatomok fokozatosan növelik a gazdarács elemi cellájának méreteit. Ez a méretnövekedés az elhajlási kép vonalrendszerének fokozatos balratolódásában jut kifejezésre.) Az elhajlási képből történő ötvözet analízis a kémia analízissel szemben különösen olyan esetekben előnyös, amikor az ötvözet több komponenst tartalmaz, s eleve nem lehet tudni, mely alkotóelemek kristályosodnak együtt.

Ha egy kristály elemi cellájának térfogatát és a kristály sűrűségét nagy pontossággal meghatározzuk, akkor a két adat szorzata nagy pontossággal megadja az elemi cella tömegét. Másrészt viszont az elemi cella tömegének egyenlőnek kell lennie az elemi cellában levő atomok atomsúlya összegének és a Loschmidt-számnak a hányadosával. Ha két tömegadat a mérési hiba határán belül eltér, akkor ez azt jelenti, hogy a rácsba vagy idegen alkotóelemek, szennyezések épültek be (többlet), vagy egyes rácspontok nincsenek betöltve (hiány). A rácsállandók mérési pontosságából következik, hogy e rácshibákat ilyen módszerrel csak akkor lehet kimutatni, ha 10 000 ekvivalens rácspontra 3-nál több hiányhely, ill. beépült idegen atom esik.

Az elhajlási képből közvetlen módszerekkel nyerhető információk felsorolását még tovább lehetne folytatni. Nem beszéltünk még róla, hogyan lehet az elhajlási képben a hőmozgás folytán fellépő diffúz foltokból a kristály rugalmas állandóit meghatározni, ugyancsak nem volt szó a fáradási és öregedési jelenségek, a plasztikus deformáció és a tartós folyás, valamint a diszlokációk vizsgálatáról stb. sem. Azonban annyit már az eddigiekből is láthatunk, hogy a röntgensugarak elhajlását tanulmányozó finomszerkezet vizsgálat igen sokoldalú, s eredményei a tudomány és technika legkülönbözőbb területein felhasználhatók.

Folytatása köv.
Sándor Endre
(Eötvös Loránd Tudományegyetem Fizikai Intézete, Bpest)

________________________