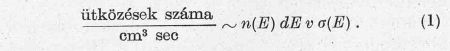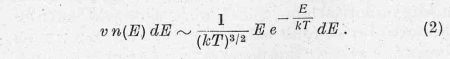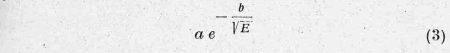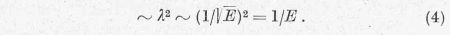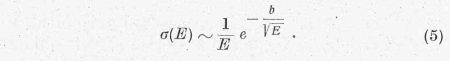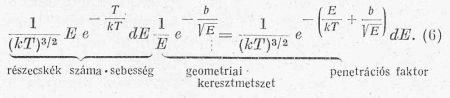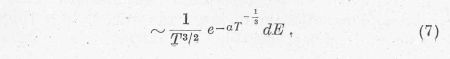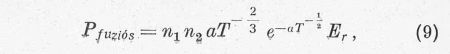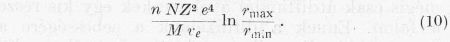Ez az energia az U-235 1 grammjára vonatkoztatva ≈ 2 · 1010 cal ≈ 1 MWnap energiát jelent, vagyis annyi energiát, amennyi egy 1 MW=1000 kW-os hőteljesítményű erőmű 1 napi üzemanyagszükségletét biztosítja.
A fúzió három, később közelebbről vizsgált alakja:
D + D = He3 + n + 3,2 MeV,
D + T = He4 + n + 17,6 MeV.
1 g D-T keverék fúziójánál felszabaduló energia 8,1 · 1010 cal ≈ 4 MWnap.
Makroszkópikus méretekben a fissziós energia-felszabadulás robbanásszerű alakja az atombombában, szabályozható alakja pedig az atomreaktorban valósult meg. A fúziós energiának jelen pillanatban földi méretekben csak a robbanásszerű felszabadulása ismert.
A fúziós energia szabályozható felszabadulásának, tehát a fúziós reaktorok megvalósításának gazdasági jelentősége igen nagy. A fúziós reaktor egyik lehetséges nyersanyaga, a deutérium gyakorlatilag kimeríthetetlen bőséggel és könnyen hozzáférhető módon áll rendelkezésünkre a tengervízben. A fosszilis energiahordozók csak néhány évszázadig elegendők, kibányászható hasadó anyagokban egy-két nagyságrenddel (kb. 25-szörösen) nagyobb az energiatartalékunk, de a tengervíz deutérium-tartalma az emberiség 1000-szeresére megnőtt fogyasztását is el tudná látni 109 évig. A fúziós reaktorok megvalósításával az emberiség valóban megszabadul az energiagondoktól. Így nem csodálatos, hogy a fúziós reaktorok kérdése mind a gazdasági, mind a tudományos élet egyik igen fontos kérdése.
A nagyhatalmak nagy anyagi és szellemi energiabefektetéssel igen intenzív kutatómunkát végeznek ezen a téren. A legutóbbi időkig csak sejteni lehetett, hogy milyen irányban keresik a probléma megoldását [1.-3.]. Egy évvel ezelőtt a szovjet eredmények egy kis részlete jelent meg [4.], majd az amerikai kutatásokról két részletesebb összefoglaló [5.-6.] látott napvilágot 1956 nyarán. Ez a két cikk sok olyan megállapítást tartalmaz, amely egybeesik a magyar kutatók e tárgyban elért és ugyancsak 1956 nyarán - a veszprémi vándorgyűlésen - nyilvánosságra hozott eredményeivel [7.-13.]. Az alábbiakban elsősorban ezek, valamint az említett két cikk alapján ismertetjük a probléma mai állását.*
A természet a lassú lefolyású, tehát nem robbanásszerűen végbemenő fúziós energiatermelésre a csillagokban mutat példát. A csillagokban lefolyó fúziós reakciókkal nem foglalkozunk [14.].
Milyen fúziós reakciók jöhetnek szóba, ha itt a Földön akarunk energiát termelni? Elsősorban azok amelyekben hidrogén-izotópok egyesülnek, mert, mint láttuk, hidrogén-készleteink szinte kimeríthetetlenek. Ezenkívül a megvalósíthatóság szempontjából is ezek látszanak a legmegfelelőbbnek.
A csillagok energiáját főleg a
e+ + e- = 2γ + 1,02 MeV,
D + p = He3 + γ + 5,5 MeV,
He3 + He3 = He4 + 2 p + 12,8 MeV
reakció-lánc és a szén-ciklus szolgáltatja [15.-18.]. Bár ezekben is hidrogén alakul héliummá, földi viszonyok között nem használhatjuk őket, mert túl lassúak. Ilyen lassú reakcióláncok csak a csillagok méreteinél tarthatnak fenn energia-egyensúlyt. Gyorsabb reakciókat kell keresni. A cikk elején említett három reakció látszik a legmegfelelőbbnek.
Vizsgáljuk meg, hogyan lelet fúziós reakciót létrehozni.
A nehéz magok hasadását a magba ütköző neutron okozza. Ahhoz, hogy egy fúziós reakció végbemenjen, az kell, hogy két atommag ütközzön össze. A két folyamat között lényeges különbség van. A neutronnak nincs töltése, ezért elektromos taszítás nem akadályozza az ütközést. Két atommag viszont csak akkor tud összeütközni, ha legyőzték a Coulomb-taszítást.
A taszítóerő legyőzésének az a legegyszerűbb módja, hogy nagy sebességgel ütköztetjük össze a részecskéket. Nagy sebességű részecskéket gyorsítóból kaphatunk, vagy, a csillagok, mintájára, a gázmolekulák nagy hőmérsékletre való felmelegítésével. Ha nagy hőmérsékletű anyagban jön létre a fúzió, a hőmozgás hatására, termonukleáris reakcióról beszélünk.
A taszítóerő legyőzésének másik módja az, hogy a mag elektromos erőterét "leárnyékoljuk".
A felsorolt lehetőségek közül a termonukleáris reakció látszik a legfontosabbnak szempontunkból, azért arról fogunk részletesebben beszélni. Előbb azonban röviden áttekintjük a többi lehetőséget.
Gyorsítók alkalmazásától mit várhatunk?
Ha gyorsítóval fúziós reakciót hozunk létre, mindig szabadul fel fúziós energia. A kérdés csak az, hogy el tudjuk-e érni, hogy több energia szabaduljon fel, mint amennyi a gyorsító működtetéséhez szükséges. A vizsgálatok azt mutatják [19.-21.], hogy ennek semmi elvi akadálya nincs. Gyakorlatilag viszont nagy nehézségekbe ütközik. A nehézségek fő oka az, hogy amikor a felgyorsított részecskék beleütköznek az atomokba, energiájuk jó részét az elektronoknak adják át, ezért a bombázó részecskének csak igen kis része hoz létre fúziót. Ha valamilyen módon lecsökkenthetnénk az elektronoknak átadott energiát, rögtön megnőne a fúziók száma, annyira, hogy még robbanás is bekövetkezhetne [10.10]. Érdemes tehát megvizsgálni, hogy milyen módon csökkenthetnénk le az elektronok energiafelvételét.
Ennek egyik módja az lenne, hogy az anyagot erős mágneses térbe tesszük. Ehhez azonban olyan erős mágneses tér kellene, amilyet nem tudunk előállítani. Egy másik lehetőség az volna., hogy igen nagy intenzitású részecske-nyalábot gyorsítunk. Erre viszont nem alkalmasak a mai gyorsítók. Megjegyezzük, hogy mostanában több helyen is próbálkoznak nagy áramerősségű gyorsítók építésével.
Akkor is csökken az elektronoknak átadott energia, ha a bombázó részecskék nem álló, hanem az előző részecskék á1tal már meglökött, mozgó elektronokba ütköznek. A számítások [12.] azonban azt mutatják, hogy ez az effektus gyakorlatilag nem okoz javulást. Tehát bár elvileg nem lehetetlen gyorsítóval energiát termelni, lehet, hogy a jövőben sikerülni is fog, ma, azonban még járhatatlan ez az út.
Az egyéb lelhetőségek közül megemlítjük Alvareznek és munkatársainak érdekes felfedezését [22.-40.].
Alvarez és munkatársai nagyarányú kutatómunkát végeznek Berkeleyben, az ott működő 6 GeV-os Bevatronnal a K-mezonok tulajdonságainak felderítésére. A K-mezonok rendszerint π vagy μ-mezonra bomlanak. A π-mezon is μ-mezonra bomlik. Így tehát a buborék-kamrában - amiben a vizsgálatokat végezték - sok μ-mezon nyom látszik. (A buborékkamra a ködkamrához hasonló berendezés, csak itt az ionizáló részecskék nem telített gőzben hoznak létre cseppeket, hanem forráspontja közelében levő folyadékban apró buborékokat.)
A K-mezonok vizsgálatánál a μ-mezonok nyomai csak zavaró hátteret jelentenek. Azonban a nyomokról készített fényképfelvételek átnézésekor néhány olyan μ-mezon nyomot találtak, ami különlegességével felkeltette a kutatók érdeklődését.
Nézzük meg az 1. ábra felső képét, ami egy ilyen felvételt ábrázol. Azt látjuk, hogy a felülről jövő μ-mezon nyoma egyszer csak megszakad. (Azt, hogy valóban μ-mezonról van szó, a pálya görbületi sugarának mérésével állapíthatjuk meg. A görbületi sugár, valamint annak a mágneses térnek az erőssége, amiben a buborékkamra el van helyezve, meghatározza, hogy milyen eszecskéről van szó.)
Tehát jött egy μ-mezon, a nyoma megszakadt, majd egyszer csak, most már más irányban, mint ahogy eredetileg repült, újra megjelent a nyoma.
Teller Ede magyar származású amerikai fizikus oldotta meg a megszakadó nyomok rejtélyét. Szerinte a következő folyamat játszódott le (kissé leegyszerűsítve: csak a lényeges lépéseket mondjuk el):
A μ-mezon találkozott a buborékkamrát kitöltő folyékony hidrogén egyik deutérium-atomjával, és befogódott egy elektronpályára. Tudjuk, hogy a negatív μ-mezonok igen hasonlóan viselkednek az elektronokhoz, többek között abban is, hogy atommagok körül keringhetnek. Az ilyen μ-mezonos atomot mezoatomnak nevezzük.
Teller szerint ha egy ilyen mezoatom találkozik egy közönséges hidragén-atommal, akkor a két mag egyesülhet, fúzionálhat. A fúizió során a μ-mezon kiszabadul, tehát nem használódik el, csak katalizálja a fúziót.
A nyom tehát azért szakad meg, mert a μ-mezon befogódik. A fúzió bekövetkezésekor kiszabadul, ezért látszik újra a nyoma. A μ-mezon nem stabil részecske, egy idő múlva elbomlik. A képen jól látszik a végső bomlásterméknek, az elektronnak a nyoma is.
Előfordulhat, hogy a kiszabadult μ-mezon újra befogódik és újabb fúziót hoz létre. Ilyen folyamatot láthatunk az 1. ábra alsó képén. Itt nem látszik olyan határozott szakadás a pályában, mint a felső képen. De a μ-mezon pályájának a megtörése nem lehet szóródás eredménye. Nyilván hamar bekövetkezett a fúzió, ezért látszik folytonosnak a pálya. A μ-mezon bomlásából keletkező elektron itt is jól látható.
Miért következik be fúzió a mezoatom és a közönséges H-atom magja között? Hiszen szó sincs a termonukleáris reakciókhoz szükséges több millió fokos hőmérsékletről! Sőt, az egész folyamat a folyékony hidrogén forráspontja alatt, -250 Co körül játszódik le.
Gondoljunk azonban arra, hogy az atomok kívülről semlegesek, mert az elektron-burok "leárnyékolja" az atommag elektromos terét. Ha tehát, pl. egy proton közeledik egy atomhoz, addig háborítatlanul halad, amíg az atom elektronburkát el nem éri. Csak akkor kezdi érezni a mag taszító hatását, amikor már az elektronburok belsejébe jutott.
Mármost a mezoatomban a μ-mezon - kb. kétszázszor nagyobb tömege miatt - sokkal beljebb kering, mint az elektron a közönséges atomban. Ugyanis a hidrogén-atom Bohr-féle elmélete szerint a keringő részecske pályájának sugara alapállapotban
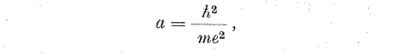
ahol ħ a Planck-állandó 1/2π-szerese, 1,05 · 10-27 erg sec, e az elemi töltés, 4,8 · 10-10 el. sztat. egység, m a részecske tömege. A pályasugár tehát fordítva arányos a keringő részecske tömegével.
De ha a μ-mezon beljebb kering, akkor egyszersmind beljebb van a mezoatom "árnyékoló burka" is, mint a közönséges atomé. Ezért a közeledő proton sokkal jobban meg tudja közelíteni a mezoatom magját, anélkül, hogy taszítást érezne. Ez pedig fúzió bekövetkezését sokkal valószínűbbé teszi, annyira, hogy még a hideg sem akadály.
Hogy valóban a leírt folyamat megy végbe, és nem valami más okozza a nyomok megszakadását, azt úgy ellenőrizték, hogy közönséges hidrogén helyett . aminek deutérium-tartalma csak 0,016% -, deutériumban dúsított hidrogénnel töltötték meg a kamrát. Ekkor a várakozásnak megfelelően megnőtt a fúziók száma.
Ilyen módon tehát szabadítható fel fúziós energia. Az a baj, hogy csak a μ-mezonok kis része hoz létre fúziót, és, ha létre is hoz, legtöbbször csak egyet. Ekkor pedig nem kapjuk vissza a μ-mezonok létrehozásához szükséges energiát sem. Olyan részecskére, lenire szükséges, amelyik tud elektron-pályán keringeni, elég nagy a tömege - lehetőleg még nagyobb, mint a μ-mezoné, mert akkor még beljebb kering -, és hosszabb életű, mint a μ-mezon, ami csak mintegy két mikroszekundumig él. Az idei rochesteri nemzetközi magfizikai konferencián szovjet kutatók beszámoltak arról, hogy Alihanjan felfedezett egy új részecskét. Ennek a tömege 550 elektrontömeg körül van, és egyéb tulajdonságai is megfelelnek a követelményeknek. Alvarez szerint ez a részecske talán alkalmas lesz fúziós energiatermelésre. Mindenesetre, egyelőre alaposan meg kell vizsgálni ennek a részecskének az összes tulajdonságát, és csak azután mondhatunk valamit arról, hogy a fúziós energiatermelésnek ez az útja járható-e.
A termonukleáris energiatermelés
A termonukleáris energiatermelés egyik módja az, ami a csillagokban is megvalósul, vagyis az, hogy stacionárius állapotban egyensúlyban van az energiatermelés és az energia elsugárzása, beleszámítva a gyors részecskék által elvitt energiát is.
Az energiatermelés másik lehetősége a rövid, robbanásszerű reakció létrehozása. A hidrogén-bombában ez valósul meg. A hidrogén-bombával nem foglalkozunk (lásd: 14.).
Elképzelhető, hogy olyan kis robbanásokat sikerül létrehozni, amelyeknek energiája gyakorlati célra hasznosítható, a rabbanómotorhoz hasonlóan. Az ilyen mikro-robbanásoknál fellépő bonyolult jelenségekről még nagyon csekély ismeretekkel rendelkezünk. A továbbiakban a stacionárius energiatermelés problémáival foglalkozunk.
A következő fizikai folyamatot vizsgáljuk:
A D vagy D-T gáz teljesen ionizált, tehát kvázisemleges plazma állapotban van. Ennek a magok és elektronok keverékéből álló gáznak a sebességeloszlását ilyen magas hőmérsékleten már a Maxwell-sebességeloszlás írja le. A gázkeverék tagjai egymással ütközés révén energia-kicserélő érintkezésben vannak, így azonos hőmérsékletűeknek tekinthetők.
Az egymásnak ütköző magok pozitív töltésük ellenére növekvő hőmérséklettel erősen növekvő valószínűséggel reakcióba lépnek egymással. A legfontosabb feladat az időegységenkénti és térfogategységenkénti azon ütközések számának a meghatározása, amelyek válóban reakcióhoz vezetnek. Ennek ismeretében ugyanis a termonukleáris reakciók fajlagos teljesítménye egyszerűen az egy reakciónál felszabaduló energiával való szorzásból adódik.
Mi lesz az így felszabaduló energia sorsa?
A legegyszerűbb esetben tegyük fel, hogy sikerült valamilyen módon a sok
millió fokos gázteret rugalmas fallal határolni, amelyről tehát a nekiütköző
részecskék energiaveszteség nélkül rugalmasan visszapattannak. Ilyenkor
energia csak sugárzás útján távozhat. A sugárzó energiát a töltött részek,
elsősorban az elektronok impulzus-változásainál fellépő fékezési sugárzás
szolgáltatja. Stacionárius állapotban a fúziós energiatermelésnek éppen
fedeznie kell az elsugárzott veszteséget. Ez az egyensúly egy minimális
hőmérsékletet határoz meg, amelynél termonukleáris reakció stacionáriusan
még éppen fennmaradhat.
Minthogy a fúziós energiafelszabadulás a magok kinetikus energiájában jelentkezik, a sugárzás révén fellépő veszteség pedig az elektronok mozgásából adódik, így magában a gáztérben állandó energiaáramlás van a magoktól az elektronok felé. A magok közepes energiája tehát kissé magasabb, mint az elektronoké. Ez annyit jelent, hogy a magok hőmérséklete és az elektronok hőmérséklete nem azonos. Az egész gázkeveréknek mint egyetlen gáznak hőmérsékletéről tehát csak első közelítésben beszélhetünk.
Mindez, amit mondottunk, csak a töltéssel ellátott reakciótermékekre vonatkozik. A neutronok energiája a fúziós tér hőmérsékletének fenntartása számára elveszett. Ez az egyensúlyi hőmérsékletet felfelé tolja.
A valóságban természetesen nem sikerül a gázt ideálisan rugalmas fallal határolni. Ezért a részecskék a falnak is adnak át energiát. Továbbá nincs tökéletesen záró fal, a fúziós tér határoló felületéről eldiffundáló részek ugyancsak visznek energiát magukkal. A falon, illetve az eldiffundálás következtében fellépő energiacsökkenés a szabad úthossz nagyságával van közvetlen kapcsolatban. Mindezen veszteségeket a fúziós energia-felszabadulás csak még magasabb hőmérsékletnél fedezheti.
Nézzük most a fentebb elmondottakat kvantitative. Meggondolásainknál
elsősorban a függvények menetére vagyunk kíváncsiak. A fontos
végeredményeket azonban vagy numerikus számításra alkalmas egyenletek
alakjában, vagy diagrammban közöljük.
Vizsgáljuk először azt a kérdést, hogy az
E és E + dE
energia-intervallumban hány reakcióhoz vezető ütközés történik, például a D
és T magok között [23.]. A reakcióhoz vezető ütközések száma az időegység
alatt arányos az ezen intervallumba eső részecskék
n(E) dE számával és az ezen energiához tartozó ν sebességgel,
valamint a reakció σ(E) hatáskeresztmetszetével:
Az E és E + dE intervallumban eső részecskék száma a
Maxwell-Boltzmann-eloszlás szerint:
Az összes arányossági tényezőket elhagytuk, de a T-től való függést a
későbbiek számára mindig kihangsúlyozzuk. Az
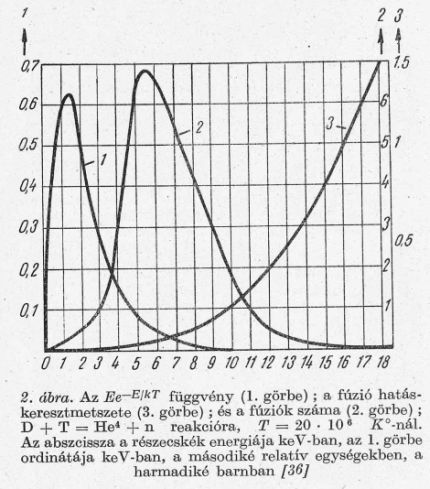
Ee-E/kT függvényt a 2. ábrán láthatjuk 20 millió fok hőmérséklet
esetén. Nagyobb energiák esetén
természetesen csak az e-E/kT
faktor a döntő.
A σ(E) hatáskeresztmetszet két tényezőből tevődik össze. Azt kell
megnéznünk, mi a valószínűsége annak, hogy egy részecske eltalálja a
másikat, - nevezzük ezt geometriai hatáskeresztmetszetnek -, azután
vizsgáljuk, mi a valószínűsége annak, hogy a két részecske fúzionál. A két
részecske eggyéolvadását, tehát a reakció első fázisát, a közbülső mag
képzését a két mag elektrosztatikus taszító tere akadályozza. Az
alagút-effektus segítségével az egyik részecske be tud hatolni a másikba
akkor is, ha energiája nem elég a Coulomb-gáton klasszikus módon való
átlendítésre. A behatolás valószínűségét az
úgynevezett Gamow-féle penetrációs faktor írja 1e. Mekkorának válasszuk a
mag "geometriai" keresztmetszetét? Nyilvánvalóan a gázkinetikai
(10-8)2cm2 nagyságrend túlságosan nagy, mert a molekula határait a keringő
elektronok pályája szabja meg. A (10-12)2cm2 nagyságú magfelületre
gondolhatnánk. A magreakciók elmélete szerint azonban a most vizsgált
reakció szempontjából a
de Broglie hullámhosszal azonos lineáris mérettel kell számolnunk Így a
geometriai hatáskeresztmetszet:
Végül is a teljes hatáskeresztmetszetet (3) és (4) szorzata adja:
D-D reakció esetén a pontos összefüggés:
Ebbe az összefüggésbe az energiát keV-ben kell behelyettesítenünk, akkor
σ (10-24 cm2) egységekben adódik.
Ezt a görbét is a 2. ábrán láthatjuk.
Most már felírhatjuk az E és E + dE tartományba
eső reakcióhoz vezető ütközések számát, ami (2)
és (5)) szorzata:
A két exponenciális kifejezés szorzatát is felrajzoltuk a 2. ábrán. Ez a
görbe meglehetősen éles maximumot ad annál az E értéknél, amelyre nézve
az
kitevő minimális értékű. E ezen optimális értékére könnyen
meghatározhatóan
Így végül az E és E + dE intervallumba eső
ütközések száma ezen az optimális helyen
Ha a reakcióhoz vezető ütközések összes számát meg akarjuk határozni,
összegeznünk kell minden lehetséges E értékre, vagyis integrálnunk kell a
(6) kifejezést E szerint a 0 - ∞
tartományra. Ezt azonban egy
közelítéssel elkerülhetjük: minthogy a görbe igen gyorsan mindkét oldalon
nullára esik, megközelítjük a görbe alatti területet egy olyan Gauss-görbe
alatti területtel, amelynek ugyanakkora a magassága és a szélessége. A
Gauss-görbe legyen tehát
arányosság olvasható ki. A (8) kifejezés már integrálható. E szerint:
Így végül a másodpercenként és térfogategységenként létrejövő ütközések
számát a következő formula adja:
Ezzel megkaptuk végső összefüggésünk függvényformáját.
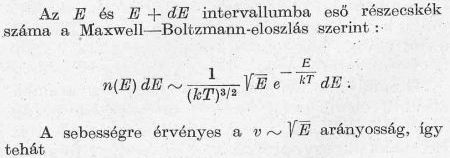
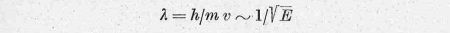
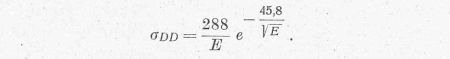
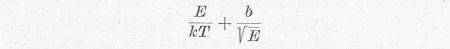

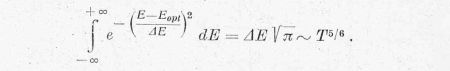
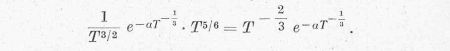
ahol az 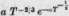 kifejezés a reakciósebesség, vagyis annak a
valószínűsége, hogy egy kiragadott 1 jelű mag reagál egy 2 jelű maggal.
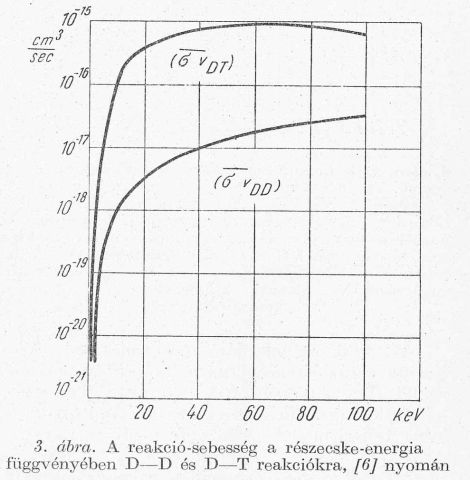
Ennek értékét a 3. ábrán láthatjuk D-D és D-T reakció esetén.
D-D reakció esetén a (9) formula így adódik:
kifejezés a reakciósebesség, vagyis annak a
valószínűsége, hogy egy kiragadott 1 jelű mag reagál egy 2 jelű maggal.
Ennek értékét a 3. ábrán láthatjuk D-D és D-T reakció esetén.
D-D reakció esetén a (9) formula így adódik:
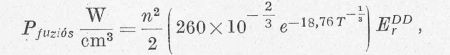
ahol n a D-magok száma/cm3, T keV-ben mérendő.
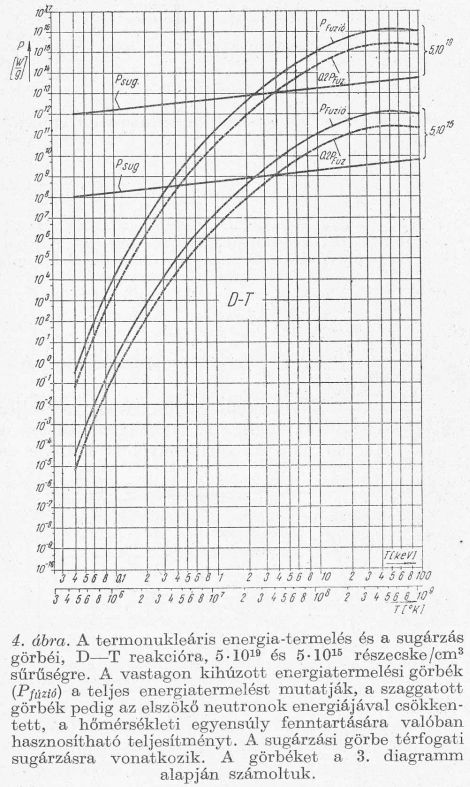
Az eddigiek alapján most már megrajzolhatjuk a fúziós energiatermelés görbéit a hőmérséklet függvényében. A 3. diagramm segítségével két különböző sűrűség esetére kiszámítottuk fajlagos teljesítményt. Ezt ábrázoltuk a 4. rajzon. Az egyik normál állapotú D2 T2 gázkeverékre vonatkozik, a másik pedig négy nagyságrenddel kisebb sűrűségre.
A görbéket mindenütt egységnyi tömegre vonatkoztattuk. D-D reakciónál:
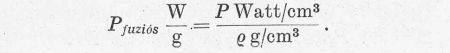
A fajlagos teljesítmény nyilván a sűrűséggel lineárisan változik. Így tetszésszerinti sűrűség esetén megkapjuk a teljesítmény-görbét a most felrajzolt görbe egyszerű párhuzamos eltolásával.
Vizsgáljuk az (1) kiindulási egyenletünkben szereplő
kifejezést. Ennek integrálja az egész energiatartományra a ν σ szorzat átlagértékét adja:
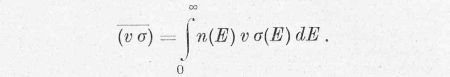
A 3. ábrán ezt - az eddigiekben reakciósebességnek nevezett - középértéket látjuk. Segítségével a teljesítmény értéke:
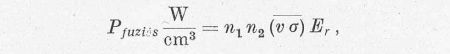
ahol n1 az egyik, n2 pedig a másik típusú részecske sűrűsége. Azonos részecskék esetén
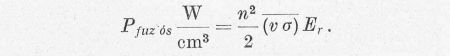
A 4. ábra görbéit ezek segítségével számoltuk ki.
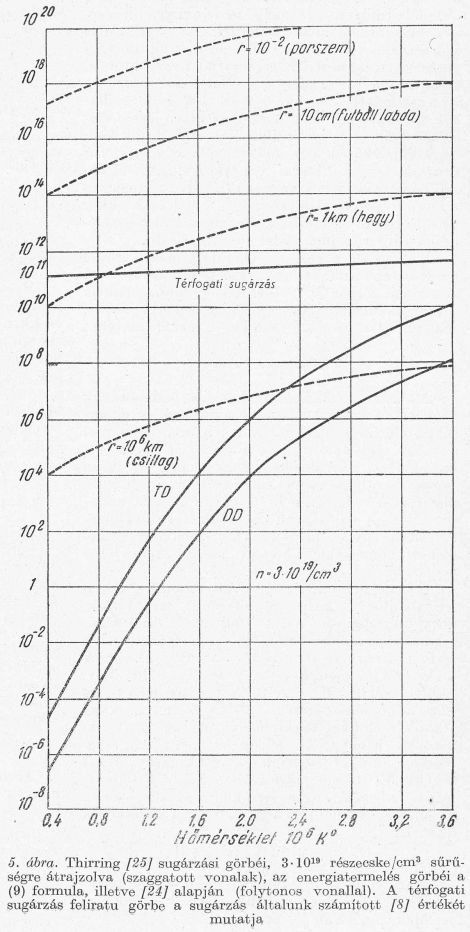
Most nézzük az energia-mérleg másik oldalát, az elsugárzott teljesítményt. Első pillanatban arra gondolhatnánk, hogy a T hőmérsékletű plazma a Stefan-Boltzmann törvény szerint a felületével és T4 hatványával arányos módon sugároz. Az 5. ábrán az így kiszámított görbéket látjuk. Adott sűrűségnél a fajlagos, tehát a tömegegységre vonatkoztatott elsugárzott teljesítmény csökkenő mérettel egyre nő, mert a felület és térfogat viszony nagy méretek felé javul. A sugárzás és az energiatermelés csak csillagászati méretekben tud egyensúlyba jutni. Ezekből a görbékből vonta le Thirring [25.] azt a következtetést, hogy a fúziós reakció földi méretekben nem látszik lehetségesnek. Ezt a pesszimista felfogást igen sokan magukévá tették. A következőkben látni fogjuk, hogy a Stefan-Boltzmann törvény itt nem alkalmazható. Ebből természetesen nem következik az, hogy a fúziós reaktor most már megvalósítható, hanem csak az, hogy a megvalósítást a most elmondottak nem akadályozzák.
Ha azonban meggondoljuk azt, hogy a tízmillió fokos plazma sugárzásának a maximuma a lágy (néhány keV energiájú) röntgensugárzás tartományába esik, rögtön beláthatjuk, hogy földi méretű plazma ilyen hőmérsékletnél - és természetesen nem túl nagy sűrűségnél - igen nagy mértékben átlátszó. A fekete sugárzás törvényszerűségei tehát messzemenően nem alkalmazhatók erre az esetre. A plazma belsejében keletkezett sugárzás gyakorlatilag abszorbció nélkül hagyja el a plazmát. Így a sugárzási veszteség is térfogati jelenség, teljesen úgy, mint az energiatermelés. A fajlagos sugárzás tehát nem függ a geometriai méretektől.
Vizsgáljuk most a térfogati sugárzás kvantitatív viszonyait.
Minthogy azonos kinetikus energia esetén az elektronok 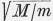 arányban
gyorsabban mozognak - itt M a mag, m az elektron tömege -, csak az
elektronok által elsugárzott teljesítményt kell figyelembe vennünk. Az
elektronok akkor sugároznak, ha a mag terében gyorsuló mozgást végeznek. Az
elsugárzott energia a gyorsulás négyzetével arányos. A magtól r
távolságban elhaladó elektron gyorsulása:
arányban
gyorsabban mozognak - itt M a mag, m az elektron tömege -, csak az
elektronok által elsugárzott teljesítményt kell figyelembe vennünk. Az
elektronok akkor sugároznak, ha a mag terében gyorsuló mozgást végeznek. Az
elsugárzott energia a gyorsulás négyzetével arányos. A magtól r
távolságban elhaladó elektron gyorsulása:
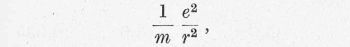
így tehát egy elektron által az időegység alatt elsugárzott energia:
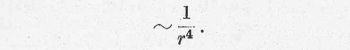
Ha a térfogategységben n elektron van, akkor azok a legkülönbözőbb r értékkel rendelkeznek egyforma valószínűséggel. Így egyetlen mag terében az n elektron által elsugárzott teljesítmény
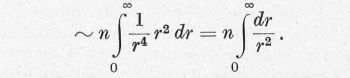
Az integrál a felső határon nullát ad, r = 0-nál azonban divergál. Ebből az következik, hogy csak az egész közel haladó elektronok eltérítése járul komoly értékkel az integrál értékéhez, másrészt az is következik, hogy az integrálás alsó határát nem választhatjuk nullának. Ha az elektron νe sebességgel mozog, helyzetének bizonytalansága ro ≈ ħ/mνe. Nincs értelme annak, hogy ennél kisebb távolságot adjunk meg. Válasszuk ezt alsó határnak, akkor az integrál értéke:
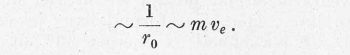
Ha most még az elektron sebessége helyett behozzuk a
νe 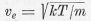 összefüggéssel
a hőmérsékletet, azt találjuk, hogy az egy elektron által
elsugárzott teljesítmény
összefüggéssel
a hőmérsékletet, azt találjuk, hogy az egy elektron által
elsugárzott teljesítmény 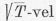 arányos. A térfogategységenként
elsugárzott teljesítmény természetesen mind a magok, mind az elektronok
számával, így végeredményben a sűrűség négyzetével arányos:
arányos. A térfogategységenként
elsugárzott teljesítmény természetesen mind a magok, mind az elektronok
számával, így végeredményben a sűrűség négyzetével arányos:
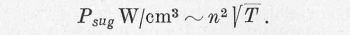
Ha most az arányossági tényezők értékét behelyettesítjük, a következő végső formulához jutunk:
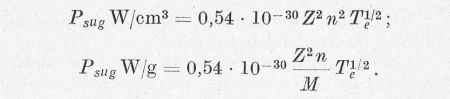
A formula itt leírt egyszerűsített levezetése Teller-től való [5.]. Pontos kiszámítása [26.]-ban található. A hőmérséklet e indexe arra utal, hogy más a magok és más az elektronok hőmérséklete.
Ebből az összefüggésből több igen fontos következtetés vonható le:
a) Az elsugárzott teljesítmény a hőmérséklet gyökével és nem negyedik
hatványával nő, mint ahogy a Stefan-Boltzmann törvény előírná.
b) A sugárzás is térfogati és nem felületi jelenség. A sűrűségtől teljesen
azonos módon függ, mint az energiatermelés görbéje. Ha tehát valamilyen
hőmérsékletnél, megadott sűrűségnél a termelt és elsugárzott teljesítmény
egyenlő, akkor bármilyen más sűrűségnél is egyenlők lesznek ugyanezen
hőmérsékletnél. Az egyensúlyi hőmérséklet tehát független a sűrűségtől, de
független természetesen a geometriai méretektől is, mert az energiatermelés
is, a sugárzási veszteség is a térfogattal arányos. Nem kell tehát
csillagászati méreteket választani, bármilyen kis térfogatban beáll ez az
egyensúly. Hangsúlyoznunk kell, hogy mindez csak a termelt energia és a
sugárzási veszteség egyensúlyára vonatkozik. Az egyéb diffúziós veszteségek
szempontjából a térfogat és a felület viszonya ismét számít. Tehát csak
akkor igazak eddigi állításaink, ha sikerült az eszményien záró rugalmas
falat megvalósítani.
A 4. és 5. ábrán az energiatermelés görbéi mellé berajzoltuk a tömegegységre vonatkoztatott sugárzási görbét is. A két görbe metszéspontja a stacionárius állapotot jelző egyensúlyi hőmérsékletet adja. Ennek értéke D-T reakció esetére:
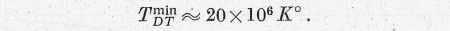
A fúziós reakció stacionárius állapotának beállásához tehát valamilyen minimális hőmérséklet elérése szükséges. Ennél a hőmérsékletnél azonban csak akkor áll be a stacionárius állapot, ha egyrészt a reakciótermékek energiája teljes egészében a hőmérséklet fenntartására fordítódik, másrészt a sugárzáson kívül egyéb energiaveszteség nincs. A valóságban egyik feltétel sincs megvalósítva, így a fúziós reaktor stacionárius üzemének hőmérséklete az itt megadottnál jóval magasabb kell hogy legyen.
Ha megnézzük, az egyensúlyi hőmérsékleten felszabaduló fajlagos teljesítményt, azt látjuk, hogy meglehetősen nagy érték, ha normál sűrűségű gázt veszünk alapul. Így 1 g D-T gázkeverék térfogata normál nyomáson ≈ 5 · 103cm3. Ennek fúziós teljesítménye ≈ 1011 cal ≈ 4 ·105 MW. A hőmérséklet T ≈ 2 · 107 K°, a nyomás pedig ezen a hőmérsékleten p ≈ 4 ·104 at. Ezek az adatok technikai szempontból elriasztók. Csökkentsük azonban a sűrűséget négy nagyságrenddel, ami azt jelenti, hogy az 1 g gázkeveréket tegyük 5 · 107cm3 térfogatba. Ekkor a teljesítmény is négy nagyságrenddel csökken, sőt a nyomás is. A technikai adatok tehát a következők lesznek:
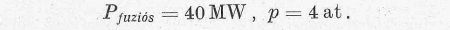
A nagyobb térfogathoz nagyobb felület tartozik. Ennek a hőelvezetés technikai megoldása szempontjából van jelentősége.
A túlságosan nagy fajlagos teljesítmény nemcsak a hatásos hőelvezetés szempontjából jelent nehézséget, de teljesen meg is hiusíthatja a stacionárius üzemet: túlságosan hamar "kiégeti" a fűtőanyagot. Folytonos üzemet tehát csak hosszabb kiégési idő esetén remélhetünk.
Az alábbi adatok felvilágosítást adnak a viszonyokról:

Most röviden még két eddig csak érintett problémát nézzünk meg közelebbről: mennyivel csökken a hőmérséklet fenntartására fordítható energia, ha figyelembe vesszük, hogy a neutronok kiviszik energiájukat a fúziós térből, továbbá azt, hogy az elektronok és a magok hőmérséklete közötti különbség az energiaegyensúlyt hogy befolyásolja. Minthogy az energia a reakciótermékek tömegével fordított arányban oszlik el az egyes magokra, a reakciómérleg így írható:
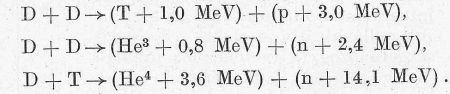
Az első két reakció körülbelül egyforma gyakoriságú, így azt látjuk, hogy D-D reakció esetén az összes reakcióenergia 66%-a a töltéssel bíró részek kinetikus energiája formájában jelentkezik. A D-T reakciónál az energia 80%-át a neutron viszi el és csak 20%-a marad a He4 számára. A 4. ábrába szaggatva berajzoltuk az elvesző energiával lecsökkentett energiatermelési görbéket is. Látjuk, hogy ezzel az egyensúlyi hőmérséklet jelentős mértékben megemelkedett:
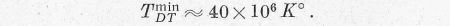
Technikai szempontból ez főleg azért baj, mert a nyomás hasonló mérvű megnövekedését is maga után vonja.
Vizsgáljuk most meg a Tm, maghőmérséklet és a Te elektronhőmérséklet közötti különbséget. Ezt abból a feltételből határozzuk meg, hogy a magasabb Tm hőmérsékleten levő magok által az alacsonyabb Te hőmérsékletű elektronoknak ütközés révén átadott teljesítmény éppen az elsugárzott teljesítményt kell hogy adja. Teller nyomán [5.] először az elektronok által a nyugvó magoknak, majd a mozgó magoknak átadott energiát határozzuk meg. Ebből a magok által az elektronoknak átadott energia is kiadódik.
A nyugvó magok között haladó elektron energiaveszteségét a hatótávolság-meghatározás analógiájára, végezzük. A magtól r távolságra haladó elektronra ható legnagyobb erő Ze2/r, az ütközés ideje ∼r/νe. Az átadott impulzust a kettő szorzata adja. Ennek négyzete a mag tömegével osztva, az átadott energiát adja:
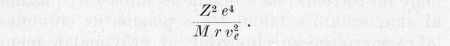
Ennek r szerinti integrálja a divergenciák elkerülése miatt valamilyen rmin és rmax érték között a
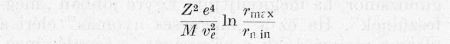
kifejezés. rmax és rmin értékét az ismert módon rögzíteni lehet. Pontos értékük nem lényeges, mert csak logaritmusuk szerepel. Ha ezt a kifejezést a másodpercenként beesett részecskék számával, nνe-vel megszorozzuk, továbbá figyelembe vesszük, hogy 1 cm3-ben N mag van, megkapjuk az egységnyi időben és térfogatban a nyugvó magoknak átadott energiát:
Mozogjanak most a magok ν « νe sebességgel. Akkor az átadott energia csökken. Fejtsük sorba az energiát ν/νe szerint és álljunk meg a másodrendű tagnál:
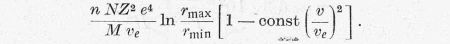
A lineáris tag nyilván nem szerepelhet a sorba-fejtésnél, mert nincs semmiféle irány kitüntetve. A konstans értékét abból a feltételből határozhatjuk meg, hogy ha Mν2 = mν2e, tehát ha a hőmérséklete azonos, nem kaphatunk energia-átadást. Ebből const = M/m adódik. Ezt úgy értelmezzük, hogy az elektronok ugyanannyi energiát adnak át a magoknak ilyenkor, mint amennyit kapnak tőlük. A második tag tehát a magok által az elektronoknak átadott energiát képviseli. A magok által az elektronoknak átadott többletenergia nem messze az egyensúlyi állapottól így közelítőleg
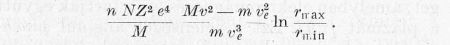
Ha most a kinetikus energia helyett a hőmérsékletet hozzuk be, a magok által az elektronoknak átadott teljesítményre a következő összefüggést kapjuk:
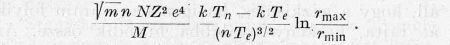
Ennek a kifejezésnek kell megegyeznie a T-vel arányos elsugárzott teljesítménnyel. Az így kiadódó
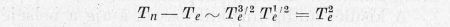
arányosságból azt látjuk, hogy növekvő hőmérsékletek félé a különbség rohamosan nő. Az arányossági faktorok számértékét is figyelembe véve a fenti összefüggés D gáz esetén a következő alakú:
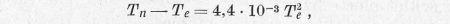
ahol a hőmérsékletet keV-ben kell mérnünk. Azt látjuk, hogy 1 keV
nagyságrendű hőmérsékletnél a különbség elhanyagolható, 100 keV
maghőmérsékletnél azonban már csak 75 keV elektronhőmérséklet adódik. Azt
látjuk tehát, hogy extrém magas hőmérsékletek esetén
még a 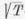 formánál is gyengébben nő az elsugárzott teljesítmény, ha
irányadónak az energiatermelésre jellemző maghőmérsékletet vesszük.
formánál is gyengébben nő az elsugárzott teljesítmény, ha
irányadónak az energiatermelésre jellemző maghőmérsékletet vesszük.
Említettük, hogy teljesen rugalmas és áthatolhatatlan falra van szükség a termonukleáris reakciók létrehozásához. A csillagokban a gravitációs erőtér tartja vissza a kiszökni akaró nagysebességű részecskéket. A termonukleáris reaktorban erről valami más módon kell gondoskodni. A plazma bezárása, nehéz, mert a reakcióhoz szükséges több millió vagy tízmillió fokos hőmérsékletet semmilyen szilárd anyag nem bírja ki. Ezért a forró plazmát a falalttól távol kell tartani.
Ezt több módon kísérelhetjük meg. Az egyik lehetőség az volna, hogy megfelelő elrendezéssel olyan nyomás és hőmérséklet-eloszlást hozunk létre a gázban, hogy egy középső forró "magot" egyre hidegebb rétegek vegyenek körül. A probléma az, hogy ilyen eloszlást stacionáriusan létre lehet-e hozni, és ha igen, mennyire stabil. A számítások azt mutatják, hogy ez az elképzelés talán megvalósítható, bár a méretekre igen nagy értékek jönnek ki [38.].
A plazma együttartásának másik lehetőségére Ronald Richter mutatott rá már régebben. Azt javasolja, hogy a csillagok gravitációs terét elektromágneses térrel pótoljuk. Ezt az teszi lehetővé, hogy bár egészében semleges a plazma, részecskéinek töltése van. Az ilyen "elektromágneses falon" természetesen a reakciók folyamán keletkező neutronok akadály nélkül áthaladnak.
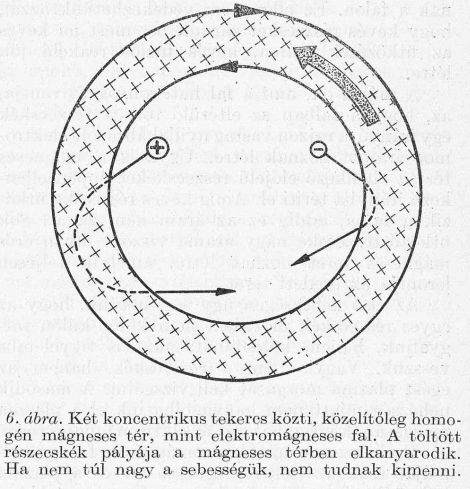
Az elektromágneses fal megalkotása nem könnyű feladat. Egy egészen egyszerű példán szeretnénk megmutatni a nehézségek természetét. A 6. rajzon láthatjuk, hogyan téríti vissza a honjogén mágneses tér a töltött részecskéket. A pozitív töltésű részecskék (atommagok) nagyobb tömegük miatt mélyebben behatolnak a "falba", mint a kis tömegű elektronok. Az egyforma részecskék közül az megy mélyebbre, amelyiknek nagyobb a sebessége.
Ha egy térrészt teljesen bezárunk homogén mágneses térből alkotott fallal, a belsejéből egy meghatározott energián aluli részecskék nem tudnak kiszökni.
Ez addig igaz így, amíg a bezárt részecskék száma igen kicsi. Ha sok részecske van bent, a fal két okból nem zár jól.
Az első az, hogy a részecskék, amíg a falban mozognak, összeütközhetnek egymással. Az ütközés letéríti őket eredeti pályájukról, és így átjutnak a falon. Ez ellen nem védekezhetünk azzal, hogy kevés részecskét zárunk be, mert ha kevés az ütközések száma, kevés fúziós reakció jön létre.
A másik ok, ami a fal hatékonyságát rontja, az, hogy a falban az eltérülő töltött részecskék egy irányú, a rajzon vastag nyíllal ábrázolt elektromos áramot hoznak létre. Ugyanis a mágneses tér az ellenkező előjelű részecskéket éppen ellenkező irányba téríti el. Amíg kevés részecske ütközik a falba, addig ez az áram nem zavar. Sok ütköző részecske nagy árama viszont olyan erős mágneses teret hozhat létre, amelyik teljesen lerontja az eredeti teret.
Az első nehézségen úgy segíthetünk, hogy az egyes részecskék mozgását nem külön-külön tárgyaljuk, hanem kölcsönhatásukat is figyelembe vesszük. Vagyis nem a részecskék, hanem az egész plazma mozgását kell vizsgálni. A második nehézség miatt nem hanyagolhatjuk el a plazma mozgásának visszahatását az elektromágneses térre.
Ezek szerint az elektromágneses fal problémáját csak az elektromágneses tér és a plazma kölcsönhatását figyelembe vevő magnetohidrodinamika segítségével lehet megoldani.
A magnetohidrodinamika olyan kontinuumok mozgásával foglalkozik, amelyekre elektromágneses erők is hatnak. Egyenleteit úgy kapjuk, hogy a hidrodinamika mozgásegyenleteibe a többi erő mellé az elektromos és mágneses erőket is beírjuk [27., 28.].
A plazma saját terének és a külső térnek a viszonylagos erőssége szabja meg, hogy hogyan kell számolnunk. Ha a plazma saját tere igen gyenge a külső térhez képest, akkor úgy számolhatunk, mintha csak egyes részecskék mozognának az elektromágneses térben. Ez a helyzet, mint láttuk, ha a plazma igen ritka. De sűrűbb plazma esetén is, ha a külső tér erősségét kellően megnöveljük. Ehhez azonban igen erős mágneses térre volna szükség.
Mit mond a magnetohidrodinamika a plazma mozgásáról?
Ha elég erős a kölcsönhatás a tér és a plazma között, akkor a mágneses erővonalak mintegy "befagynak" a plazmába. Ez azt jelenti, hogy a részecskék zavartalanul mozoghatnak az erővonalak irányába, de ha az erővonalakra merőlegesen elmozdul a plazma, az erővonalak mennek vele együtt.
Megfordítva, ha az erővonalak mozognak, a részecskék nem tudnak "leszakadni" róluk, hanem csavarvonalon körülöttük repülve követik őket. Ez természetesen csak durva közelítés, de jó áttekintést nyerítetünk a viszonyokról ilyen módon.
Próbáljuk elképzelni ennek a képnek az alapján, hogy mi történik, ha a mágneses falba zárt plazma ki akar szökni a falon. Ha a plazma az erővonalakra merőlegesen elmozdul, az erővonalak mennek vele együtt. Az erővonalakból álló fal tágulni kezd. De az erővonalak úgy viselkednek, mint a gumizsinór, ha megnyújtjuk. Egyre jobban "megfeszülnek". Ha ez a "mágneses nyomás" eléri a plazma nyomásának a nagyságát, a tágulás megszűnik, a plazma nem jut tovább, nem tud kiszökni.
Minden rendben lenne, ha szigorúan igaz lenne, hogy a részecskék nem tudnak elszakadni az erővonalaktól. De az csak addig igaz, ameddig egy ütközés le nem téríti őket eredeti pályájukról. Ha az ütközéseket is figyelembe vesszük, mégis csak átdiffundál a részecskék egy kis része a falon. Ennek a diffúziónak a sebességére a magnetohidrodinamika a következő értéket adja (deutérium-plazma esetén):
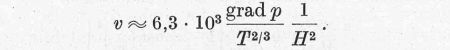
Itt p a plazma nyomása, T a hőmérséklete KeV-ban, H pedig a mágneses tér erőssége. Láthatjuk, hogy a mágneses tér erősségének növelésével a diffúzió erősen lecsökkenthető.
Az ilyen falak hátrányos tulajdonsága, hogy instabilak, ha valami zavaró hatás éri őket, könnyen "elszakadnak". Egy példán látni fogjuk, hogy hogyan kell ezt érteni.
A fizikusok már régóta ismernek egy jelenséget, amelyben elektromágneses erők tartják együtt a plazmát [29.]. Ezt a jelenséget angolul pinch-effektusnak nevezik, ami magyarul körülbelül annyit jelent, hogy összeszorítási effektus. Nincs még jó magyar neve.
A pinch-effektus igen egyszerű jelenség, abból áll, hogy a gázkisülés, ha igen nagy áram folyik át rajta, keskeny nyalábbá húzódik össze. Az összehúzódás oka az, hogy párhuzamos áramok vonzzák egymást, a kisülés pedig sok vékony áram-fonalból állónak képzelhető.
A kisülés addig húzódik össze, amíg a belsejében levő plazma nyomása el nem éri az összehúzó elektromágneses erők nyomását. Összehúzódáskor a plazma melegszik, emiatt nő a nyomása. Az összehúzódás megáll, ha a hőmérséklet elérte az
egyenlet által megszabott értéket. I a kisülésben folyó áram erőssége, N a kisülés 1 cm hosszú részében levő részecskék száma, T a hőmérséklet, Kelvin-fokban, k a Boltzmann-állandó.
Nagy hőmérséklet esetén igen nagy áramra van szükség. Ha pl. a plazma 10 millió fokra melegszik fel, 800 000 Amper kell az összehúzásához. Ez azt mutatja, hogy stacionárius üzemben a pinch-effektus nem használható.
A pinch-effektus példáján szeretnénk még megmutatni, hogy kell érteni az elektromágneses falak már említett instabilitását [30.].
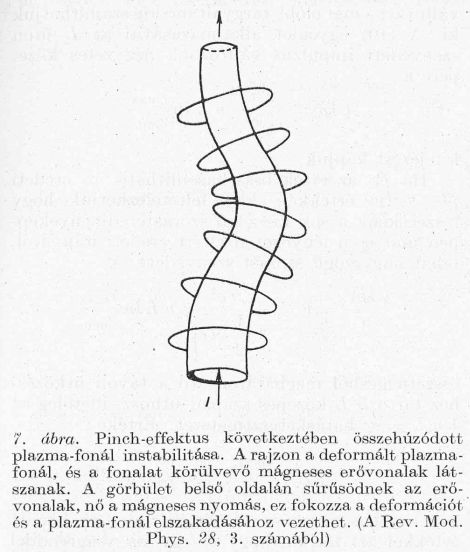
A 7. rajzon a keskeny nyalábot alkotó plazmát látjuk, s a plazmában folyó áram mágneses terének erővonalait. A plazma-nyalábot valami deformálta, a közepén kihajlott. Jól látszik a rajzon, hogy a görbület belső oldalán sokkal sűrűbbek a mágneses erővonalak, mint a külsőn. Emiatt a térerősség négyzetével arányos mágneses nyomás is nagyobb. A baloldali nagyobb nyomás még jobban deformálja a plazma-nyalábot, egészen addig, amíg már nem bírja tovább a kihajlást és elszakad.
Stacionárius üzemben, mint mondtuk, a pinch-effektus nem használható elektromágneses falként. Nagyon hasznos azonban, ha rövid, nagy áramerősségű, nagy hőmérsékletű kisülést akarunk létrehozni. Ilyen kisülésekkel esetleg megoldható a fúziós energia mikro-robbanások útján való felszabadítása. Ehhez az kell, hogy kis mennyiségű gázt a fúzióhoz szükséges hőmérsékletre melegítsünk fel. A felmelegítést impulzusszerű, nagyenergiájú kisüléssel végezhetjük.
Ilyen kísérletek több helyen is folynak, Amerikában [31.-33.], Angliában [34.-35.], a Szovjetunióban [4.]. A kísérletek eredményéről, a hidrogénbombára való tekintettel, nagyon keveset hoztak nyilvánosságra. Annyit tudunk, hogy már félmillió amperes pillanatnyi áramerősséget is értek el nagy kondenzátorok hirtelen kisütésével. A szovjet kísérletek során az óriási áramerősség hatására összehúzódó és felmelegedő plazmában neutronokat észleltek, ami magreakciók lefolyásának kétségtelen jele.
Ezzel kapcsolatban azonban meg kell jegyeznünk valamit. Ha a fentebb megadott képlet alapján kiszámítjuk, hogy a félmillió amperes áramerősségnél mennyire melegszik fel a plazma, kisebb hőmérsékletet kapunk, mint ami a fúziós reakcióhoz szükséges. Az észlelt neutronintenzitás sokkal nagyobb volt, mint amit a hőmérséklet alapján vártak.
Ennek az a magyarázata, hogy amikor az elektromágneses erők összehúzzák a plazmát egy vékony fonallá, akkor az elektronok és az ionok egyforma sebességgel mozognak. Emiatt a kis tömegű elektronok energiája sokkal kisebb, mint az ionoké, illetve magoké. Vagyis az energia majdnem teljesen a reakciókat létrehozó magok gyorsítására fordítódik.
Említettük, hogy gyorsítókkal azért nem lehet számottevő mennyiségű energiát felszabadítani, mert a bombázó részecskék energiájának jórészét az elektronok veszik fel. Ezekben a kísérletekben viszont úgy gyorsulnak a részecskék, hogy az elektronok alig vettek fel energiát. Érdemesnek látszik ezt a kísérletekben előre nem várt effektust mesterségesen létrehozni. Vagyis egy plazmagyorsítót csinálni, amelyben megfelelően változó elektromágneses tér mozgatja a plazmát.
Két próbálkozást említünk még az elektromágneses fal létrehozására [9.].
A fúzió szempontjából jó lenne, ha nem plazmában, hanem elektronok nélkül, csupa atommagból álló gázban folynának le a reakciók. Ennek azonban igen súlyos akadálya az, hogy már viszonylag kevés mag elektrosztatikus tere is igen erős, ezért csak igen-igen kevés magot lehetne elektrosztatikus erőkkel bezárni. Mármost meg lehet próbálni azt, hogy periódikusan változó elektrosztatikus térbe felváltva pozitív magokat és negatív elektronokat teszünk. Azt remélhetjük, hogy a szomszédos ellenkező előjelű töltések vonzó hatása folytán ilyen módon több töltést lehet majd bezárni, mintha csak egyféle töltéssel próbálkozunk. A számítás azonban azt mutatja, hogy ilyen módon nem érünk célhoz. Az elektrosztatikus töltés hatását csak akkor győzhetjük le, ha az ellenkező előjelű töltéseket egészen összekeverjük. Vagyis visszajutunk ahhoz, hogy plazmával kell dolgozni.
A másik próbálkozás alapötletét Ferminek egy cikke adta, amelyben a kozmikus sugarak felgyorsulásáról is ír [39.].
Ha inhomogén mágneses térben halad egy töltött részecske, olyan csavarvonalon mozog, amelyik egy "erővonal-csövet" fog körül [27.]. Ahogy egyre nagyobb térerősségű helyre ér, egyre laposabbak lesznek a csavarvonal menetei. Ugyanis az inhomogén mágneses térnek a csavarvonal tengelyére merőleges komponense a részecske tengelyirányú sebességét egyre csökkenti. Egy, a kezdeti adatok által meghatározott térerősségű helyet elérve a részecske sebességének tengelyirányú komponense 0 lesz, majd ellenkező irányba fordul, a részecske egyre táguló csavarvonalon visszamegy. Ha két mágnespólus közt létesítünk inhomogén teret, a részecske mindkét pólus előtt visszafordul, vagyis ide-oda repked a pólusok között.
Ennek a modellnek is az a hibája, ami az egyszerű, homogén falnak, hogy ütközések révén kiszóródnak a részecskék a pólusok közötti térből. Ezenkívül azok a részecskék is ki tudnak menni, amelyeknek a sebessége csak igen kis szöget zár be az erővonalakkal. Vagyis a fala pólusoknál "lyukas".
Amint látjuk, a falak főhibája, hogy az ütközések miatt a részecskék átjutnak rajtuk. Vizsgáljuk meg ezt a folyamatot egy kicsit részletesebben.
Legyen a mágneses tér olyan erős, hogy könnyen vissza tudja hajlítani még a magok pályáját is. A fal tehát teljesen zár. Ha azonban a mágneses tér belsejében két részecske ütközik, akkor távolabb juthat a fal belsejébe. Véges valószínűsége van annak, hogy sok ütközés után a részecske átjusson a fal túlsó oldalára. Az átjutás valószínűsége annál kisebb, minél erősebb a mágneses tér és minél kevesebb az időegységre eső ütközések száma. Így a szabad úthossz növelésével a diffúzió eredményesen csökkenthető.
A szabad úthossz csökkentésének legegyszerűbb módja a sűrűség csökkentése.
A szabad úthossz definiáló egyenlete ugyanis
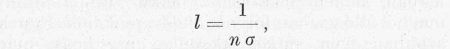
ahol σ annak a folyamatnak a hatáskeresztmetszete, amelyre vonatkozóan a szabad úthosszat vizsgáljuk. A fenti összefüggést úgy értelmezhetjük, hogy ha minden egyes részecskére egy σ nagyságú céltáblát rakunk, akkor az 1 cm2 alapú és l hosszúságú hasábban a táblácskák összfelülete éppen befedi az 1 cm2 alapot.
A diffúzió szempontjából természetesen a rugalmas ütközés szabad úthossza számít. Közbevetőleg megjegyezzük, hogy a reakció szabad úthossza, tehát az az út, amelynek befutása után egy kiszemelt részecske fúzionál, D-T reakciónál 1016 részecske/cm3 sűrűség és 10 millió fok hőmérséklet mellett 109 cm = 10 000 km nagyságrendű. Ez a távolság a Föld átmérőjével mérhető össze.
Az energiaközlő, tehát rugalmas ütközés hatáskeresztmetszetét töltött részek között a klasszikus Rutherford-szórás formulája írja le. A kölcsönhatást két típusra lehet bontani: a közeli ütközésre, amely nagyszögű szóráshoz vezet egyetlen aktusban, és a távoli ütközések kis impulzusváltozásaiból statisztikusan összeadódó kölcsönhatásra. A közeli ütközés keresztmetszetéül azt a legkisebb távolságot lehet a hatáskeresztmetszet sugarának tekinteni, amennyire az E relatív energiájú részecskék egymást meg tudják közelíteni. Egyszeres töltést feltételezve az E = e2/rk összefüggésből a hatáskeresztmetszetre a következő érték adódik:
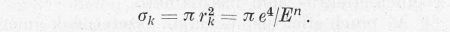
Ha az eddigieknek megfelelően E-t keV-ban fejezzük ki,
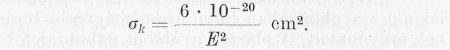
Ha most a távoli ütközéseket nézzük, az egy aktusban átadott, illetve elszenvedett impulzusváltozást a már előbb tárgyalt módon számíthatjuk ki. A (10) egyenlet alkalmazásával az L úton szenvedett impulzus változások négyzetes közepére a
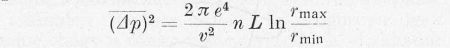
kifejezést kapjuk.
Ha ez az érték összehasonlítható az eredeti p2 = (Mν)2 értékkel, akkor feltételezhetjük, hogy részecskénk a sok kisszögű szórás eredményeképpen már igen lényegesen eltért eredeti irányától, tehát nagyszögű szórást szenvedett. A
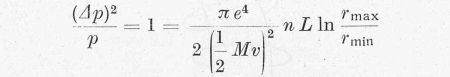
összefüggésből meghatározható a távoli ütközéshez tartozó L közepes szabad úthossz, illetőleg az 1/n L = σt hatáskeresztmetszet. Értéke:

Összehasonlítva σt számértékét a σk-ra kapott értékkel azt látjuk, hogy σt egy nagyságrenddel nagyobb, így első közelítésben elegendő csak ennek értékét figyelembe venni.
Az ütközési hatáskeresztmetszet az energia négyzetével csökken. A fúziós reaktorokban szereplő hőmérsékletnél a gázkinetikai (10-16 cm2) és a magfizikai (10-24 cm2) hatáskeresztmetszet közé esik. 1 keV hőmérsékletnél, ami ≈ 10 millió foknak felel meg, a hatáskeresztmetszet σ ≈ 10-19 cm2. Ha a sűrűség n = 1016/cm3, a szabad úthossz értéke 160 cm-nek adódik. Ennél jóval nagyobb lineáris dimenziójú térrész jelenségei már a közönséges gázkinetikai módszerekkel tárgyalhatók. A 160 cm átmérőhöz azonban ennél a sűrűségnél már óriási teljesítmény tartozik. A tízszeres szabadúthossznak megfelelő átmérőjű gömb teljesítménye pedig technikailag felhasználhatatlanul nagy értéket ad.
Ebből látjuk, hogy egy technikai teljesítményt szolgáltató fúziós reaktorban a fúziós tér lineáris mérete egy-két nagyságrenddel kisebb, vagy legjobb esetben akkora, mint az ütközési szabad úthossz, a reakció szabad úthosszánál pedig sok nagyságrenddel kisebb. A mag tehát gyakrabban fog a falnak ütközni, mint egy másik magnak.
A szabad úthossz nagy értékével jár együtt a hővezetés igen nagy értéke is. Így elvileg elképzelhető, amit már említettünk, hogy a D-T gáz néhányszor 107 K° nagyságrendű izzó magját fokozatosan csökkenő hőmérsékletű gázréteg vegye körül, amely a részecskék diffúzióját megakadályozza. Utalások találhatók arra, hogy ilyen "izobár csillagnak" nevezhető képződmény földi méretekben elvben megvalósítható [22.]. A számítások [38.] azt mutatják, hogy a méretei igen nagyok.
Érdemes megemlíteni az ilyen "csillagok" méretének egy csökkentési lehetőségét: olyan nagy anyagsűrűséget kell létrehozni, hogy az elektrongáz teljesen elfajult állapotban legyen [37.]. (Ilyen állapot a természetben a fehér törpecsillagokban található). A sugárzási teljesítmény kisebb lesz, mert ilyenkor a legtöbb energianívó be van töltve és így a sugárzáshoz vezető átmenetek száma a Pauli-elv miatt erősen lecsökken. Az energiatermelés és sugárzás közti egyensúly tehát kedvező irányba tolódik el. A szükséges sűrűséghez azonban olyan nagy nyomás és teljesítmény tartozik, ami megakadályozza ezen effektus gyakorlati felhasználását.
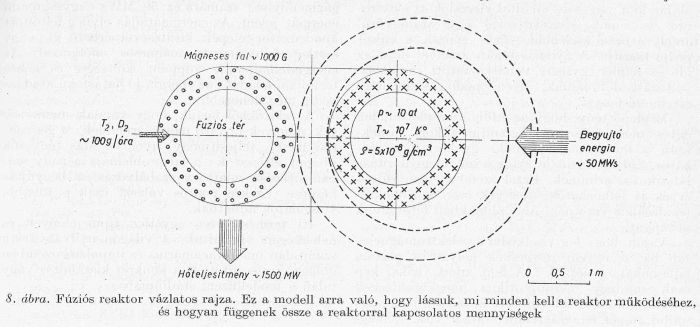
Kíséreljük meg egy, ha csak elvben is, de működő fúziós reaktormodell felvázolását. A begyújtó, szabályozó, és a stabilitást biztosító berendezéseket csak jelezzük (8.rajz).
Egy ilyen modell két célt szolgál: először lehetőséget ad arra, hogy koherens formában lássuk és formulázzuk a megoldandó problémákat, másodszor, hogy lássuk azon fizikai mennyiségek nagyságrendjét, amelyek a fúziós energiatermelésnél szerepet játszanak. Ez a vázlat nem egy igazi reaktor prototípusa. Sőt, tisztában vagyunk azzal a veszéllyel is, hogy esetleg helytelen, zsákutcába vezető kutatási irányt jelöl ki.
Vegyünk 1 g D-T keveréket. Zárjuk be ezen gázmennyiséget egy 20 m3 nagyságrendű térfogatba, akkor sűrűsége 5 · 10-8 g/cm3 = 1,2 · 1016/cm3, nyomása pedig ≈ 0,2 Hgmm lesz szobahőmérsékleten.
Az egyensúlyi hőmérsékleten a fúzióval előálló teljesítmény, amely ekkor a sugárzási teljesítménnyel egyenlő
Ez a mindenlapi gyakorlat szempontjából, összehasonlítva egy hazai erőmű 100 MW teljesítményével, rendkívül nagy érték, de nem lehetetlenül nagy. Nagyságrendben a teljes országos fogyasztással mérhető össze. Ennek elvezetése a határoló felületről nehéz, de nem megoldhatatlan probléma. Egyébként ha a térfogatot tízszeresére vesszük, azonos, 1 g összmennyiség mellett, a sűrűség és így a fajlagos teljesítmény is tizedére, egy normál erőrmű 150 MW teljesítményére csökken. Ezzel azonban nőnek más, később említendő nehézségek. Az 1 g gázmennyiség ezt a teljesítményt néhány 100 sec időtartamig tudja szolgáltatni. Így az elhasznált anyag pótlása nem ütközik technikai nehézségbe.
A bezárt gáz hőmérséklete mindenesetre magasabb, mint 20 millió fok. Elvileg bezárhatjuk egy tórusz-gyűrű segítségével. Ha a mágneses térerősséget 1000 G értékűnek választjuk, akkor 50-100 cm vastagságú fal már áthatolhatatlan lesz minden részecske számára. A részecskék diffúziója, és ennek megfelelően a belső hőmérséklet éppen a falvastagság segítségével változtatható. Egy megadott vastagságnál a nagyenergiájú részecskék eldiffundálása növekvő hőmérséklettel igen erősen nőni fog. Ez a jelenség elvileg biztosíthatja a stabilis működés feltételeit.
Az azonos energiával bíró elektronok és deuteronok különböző mélységig hatolhatnak be a mágneses falba. Így, ellentétben a belső tér neutrális plazmájával, negatív tértöltést találunk a fal szélén és pozitív tértöltést a belsejében. A megfelelő helyre felfogó elektródákat téve, közvetlenül hasznos villamos energiát kaphatunk a fúziós energia rovására. A sugárzás útján eltávozó energiát hővé alakíthatjuk és felhasználhatjuk a szokásos módon villamos energia előállítására, vagy félvezetők segítségével ezt is közvetlenül alakíthatjuk villamos energiává.
Az egyensúlyi hőmérsékletnél a gáznyomás kb. 10 at. Ez néhányszor 10 tonna erőt jelent a szolenoid egy menetére, ha méterenként 10 menettel számolunk. A 6. ábrán láthatjuk, hogy hogyan alakul ki a mágneses fal által visszalökött elektronok és ionok közvetítésével egy áramgyűrű, amely a belső szolenoid-gyűrűt vonzza, a külsőt pedig taszítja. A nyomás tehát, amelyet mint az idő és felület-egységre vonatkoztatott impulzusváltozást definiálunk, ilyen módon szemléletes értelmezést nyer.
Meglepő tény, hogy az eddig szereplő minden egyes mennyiség nagyságrendje akkora, amekkora a mindennapi mérnöki gyakorlatban szokásos. Ebből a fúziós reaktor közeli megvalósítása látszik valószínűnek. Ezzel szemben igen súlyos érvek is felhozhatók, amelyek ezen konstrukció feladásához vezetnek. Az alábbiakban felsorolunk néhányat.
Vajon, hogy fog viselkedni az elektromágneses fal, ha az egyedi részecskék helyett a plazma kölcsönhatást nézzük? A fent adott fizikai kép csak mintegy aszimptotikus megközelítésnek tekinthető. Az előbb említett áramgyűrű ugyanis millió amper nagyságrendű áramot visz. A mágneses térre való visszahatás ilyen módon nem hanyagolható el. A pontos tárgyaláshoz a magnetohidrodinamika egyenleteit kell megoldani.
Eddig nem volt szó a reakciótermékek visszatartásáról. A neutron energiáját általában a hőmérséklet-fenntartás szempontjából elveszettnek tekinthetjük, mert azok elszöknek a reakciós térből. Így az egyensúlyi hőmérséklet magasabb lesz az eddig figyelembe vettnél és ezáltal a nyomás is nő. A töltéssel bíró részek hatásos visszatartásához legalább egy nagyságrenddel erősebb fal kell.
Az energia-közlő rugalmas ütközésekhez tartozó szabad úthossz, méginkább a magreakciókhoz vezető ütközések szabad úthossza túlságosan hosszú. Az atommagok ezért, mint már fentebb láttuk, sokkal gyakrabban ütköznek a mágneses falnak, mint egymásnak. Ilyen módon igen nagy valószínűsége van a tekercs meneteivel való ütközésnek. A menetek felülete tehát a lehető legkisebb kell hogy legyen. Másrészt tízezer amper nagyságrendű áramokat kell vinniük a mágneses tér létrehozására és ugyanakkor tíz tonnányi erőket kibírniuk. Ezenkívül még hűteni is kell, ámbár a felületegységre eső teljesítmény nem túl nagy, ezenkívül a tértorzulás a tekercs közvetlen közelében valószínűleg szintén csökkenti a menetekbe ütköző részecskék számát. Ez a tény nem engedi a sűrűség és így a fajlagos teljesítmény kedvező értékre való csökkentését, mert akkor a szabad úthossz még jobban megnő. Az itt megadott konstrukció lehetősége ellen ez a legsúlyosabb érv. Mindezek a megfontolások arra, utalnak, hogy a menetek nélküli mágneses falaknak lesz különlegesen nagy szerepük, mint amilyen a pinch-effektus révén is létrejön.
A szabályozás lehetőségét természetesen csak akkor lehet megoldani véglegesen, ha kvantitatíve ismerjük azt a korrekciót, amelyet az elsugárzott teljesítmény értékében a diffúzió okoz.
Hogy megindíthassuk a fúziós folyamatot, azaz a reaktort begyújthassuk, minden részecskével néhány keV energiát kell közölni. Az egész gázmennyiség számára ez 50 MWs nagyságrendű energiát jelent. Az energiaátadás elvileg feltöltött kondenzátor-telepek kisütésével érhető el, vagy esetleg felhalmozott mágneses energiával. Az energiafelhalmozás roppant költséges és nehéz technikai feladat: az energia jó hatásfokú átadása, pedig még nehezebb.
Az előzőkből látjuk, hogy vannak mennyiségek, amelyek bíztató nagyságrendűek: a geometriai méret, teljesítmény, nyomás. Más tényezők viszont elriasztók: a fal problémája a nagy szabad úthossz miatt, a szabályozás, a begyújtás kérdése. Ezekre pontos választ csak a további vizsgálatok adhatnak.
Itt természetesen egyetlen típus előnyeit és nehézségeit vizsgáltuk. A világon nyilvánvalóan számtalan más, stacionárius és impulzus-üzemben dolgozó típus jutott el a konkrét kiszámítás vagy talán a modellüzem stádiumába.
A fizikus számára a fúziós reaktorokkal kapcsolatos kérdésfelvetés egészen általánosan így hangzik: Megoldandó a fúziós reaktor problémája. Azok a kutatók, akik a fúziós reaktorok problémáival foglalkoznak, szilárdan meg vannak győződve, hogy a gyakorlati megvalósítás a nem nagyon távoli jövőben várható. A probléma megoldásaként azonban az is kiadódhat, hogy a fúziós reaktorok - vagyis a szabályozható fúziós reakció - földi méretekben való megvalósítása nem lehetséges. Mind a megvalósítás maga, mind a megvalósítás lehetőségének tagadása csak a fizika teljesen új ágainak kifejlesztésével lehetséges. Ebben, tudniillik az új kutatási irányok kijelölésében, új, önmagukban érdekes fizikai eredmények elérésére való ösztönzésben látja a fizikus a fúziós reaktorok kérdésével való foglalkozás legnagyobb jelentőségét.
Pócs Lajos-Simonyi Károly
Központi Fizikai Kutatóintézet
Atomfizikai Osztály
1. Fusion reactors - when? Nucleonics, 13, 9 (Oct.
1955)
2. From Perhapsatron to Columbus. Nucleonics, 13, 25. (Dec.
1955).
3. Thermonuclear power - the search for ideas. Nucleonics, 14, 42 (Feb.
1955).
4. I. V. Kurchatov: Thermonuclear fusion. Engineering, No. 4705, 322 (May
11. 1956) ; ezenkívül Arcimovics,Leontovics és munkatársaik öt cikke az
Atomnaja Energija 1, 3. számában (1956).
5. E. Tellet: Generál problems of the controlled thermonuclear process.
Nuclear Seience and Engineering, 1, 313 (1956).
6. R. F.Post: Controlled fusion research. Rev. Mod. Phys. 28, 338
(1956).
7. G. Kálmán, L. Pócs, G. Schmidt, K. Simonyi: On the possibility of
controlled power production using thermonuclear fusion. Periodica
Polytechnica, 1, No. 1 (1957).
8. Schmidt György: Nagyhőmérsékletű plazma sugárzása. KFKI Közlemények, 5,
57. (1957).
9. Pócs Lajos, Schmidt György: Az elektromágneses fal problémájáról. KFKI
Közlemények, 5, 64. (1957).
10. Kálmán Gábor: Fúzió tiszta deuteron-gázban. KFKI Közlemények, 5, 73.
(1957).
11. Klopfer Ervin: Az energia ekvipartició egy szélsőséges esete. KFKI
Közlemények, 5, 84. (1957).
12. Temes Gábor: Korreláció részecskék energiaveszteségei között. KFKI
Közlemények, 5, 78. (1957).
13. Simonyi Károly: Egy fúziós reaktor vázlata. KFKI Közlemények, 5, 99.
(1957).
14. Szalay Sándor, ifj. Berényi Dénes: Termonukleáris atommagfolyamatok és a
hidrogén-bomba. Fizikai Szemle, VI, 145 (1956).
15. H. A. Bethe, C. L. Critchfield: 'I'he formation of deuterons by proton
combination. Phys. Rev. 54. 248 (1938).
16. H. A. Bethe: Energy production in the stars. Phys. Rev. 55, 434
(1939).
17. E. E. Salpeter: Nuclear reactions in the stars I. Phys. Rev, 88,547
(1952).
18. L. H. Aller: Astrophysics. New York, 1954.
19. P. E. O'Meara: An enhanced reactor. Phys. Rev. 89, 982
(1952).
20. K. Simonyi: Über die Möglichkeit der Nutzbarmachung der Atomenergie
ohne. Kettenreaktion. Acta. Phys. VI. 157 (1956).
21. Simonyi Károly: Az atomenergia hasznosításának lehetősége. KFKI
Közlemények, 4, No. 1, 83 (1956).
22. A flux for fusion. Engineering, 58, Jan. 11.
(1957).
23. F. Gamow, C. L. Critchfield: Theory of atomic nucleus. Oxford.
1949.
24. L. Ridenour: Scientific American, 182, No. 3, l1
(1950).
25. H. Thirring: Thermonuclear power reactor - are they feasible?
Nucleonics, 13, 62 (Nov. 1955).
26. W. Heitler: The quantum theory of radiation. Oxford,
1954.
27. H. Alfvén: Cosmical electrodynamics. Oxford,
1.950.
28. S. Lundquist: Studies in magneto-hidrodynamics. Arkiv för fysik, 5, nr
15, 297 (1952).
29. W. H. Bennett: Phys. Rev. 45, 890 (1934).
30. M. Kruskal, M. Schwarzschild: Proc. Roy. Soc. (London) A 223, 348
(1954).
31. W. H. Bostick, M. A. Levine, L. S. Combes: Spectrographic evidence for
the existence of the pinch effect. Sci. Rep. No. 2. 'I'ufts College
(1952).
32. H. Fischer: Short electrical breakdowns. AFCRT-TR-54-100, Office of
Techn. Services. Washington (1954).
33. R. E. Vollrath, .J. A. R. Samson: Obtaining high temperatures for
nuclear fusion. Bull. Am. Phys. Soc. 30, No. S, 9A (1955).
34. A. A. Ware: A study of a high-current toroidal ring discharge. Phil.
Trans. Roy. Soc. A 243, 197 (1951).
35. S. W. Cousins, A. A. Ware: Pinch effect in a highcurrent toroidal ring
discharge. Proc. Phys. Soc. (London) B 64, 159 (1951).
36. Termonukleáris reakciók. Nagy Szovjet Enciklopédia, 42.
kötet.
37. Marx györgy: szóbeli közlés.
38. K. Simonyi, M. Uzsoki: On the izobar D-T stars. Periodica Polytechnica,
sajtó alatt.
39. E. Fermi: On the origin of cosmic radiation. Phys. Rev. 75, 1169
(1949).
40. K. Gottstein: Die Katalyse eines Kernsfusionspozeses durch Mü-Mesonen
Phys. Blxxxütter, 13, 165 (1957).
41. W. B. Thompson: Thermonuclear power: A theoretical introduction. Nature.
179, 886 (1957)
42. J. G. Linhart: Power from thermonuclear reactions. Nuclear Engineering,
61 (Febr. 1957.).
* E cikk nyomdába adása után még két ilyen tárgyú
cikk jelent meg [41., 42.], ezek semmi lényeges újat nem tartalmaznak.