Fizikai Szemle honlap |
Tartalomjegyzék |
Károlyházy Frigyes
ELTE Elméleti Fizika Tanszék
Kedves kartársak, ugye ismerős? És hogy miért jut eszembe? Azt a feladatot kaptam, hogy a gravitációról mondjam el az igazságot, különös tekintettel az általános iskolai 6. osztályos új fizika könyv körül lezajlott vitákra. De nem sok értelme lenne a gravitációról elszigetelten beszélni. Először általában a modern fizika és a "józan ész" viszonyáról kell néhány szót szólni, mert a megfelelő háttét~ nélkül a gravitáció jelenségének modern fizikai értelmezése a levegőben lógna és képtelenségnek hatna.
Mi a lényeges különbség a modern és a klasszikus természettudomány között?
A klasszikus fizika nagymértékben leíró jellegű. Vannak hajlékony tárgyak és vannak törékenyek. A vas mágnesezhető, a réz nem. És így tovább. Ez persze nem azt jelenti, hogy mindig, minden egyes tényt külön-külön a tapasztalatból merít. A klasszikus fizika is összefüggéseket keres s ezért gyakran szorul logikai következtetésekre, elvont gondolkodásra. Közben azonban - és ezen van a hangsúly - lépten nyomon támaszkodik a köznapi szemléletre, a mindennapos tapasztalatokra. Ebben sincs semmi kivetnivaló. Sőt szentül hiszem, hogy az általános iskola ma sem tehet okosabbat, mint hogy a mindennapos jelenségek körében igyekszik a megfigyelőképességet és a kínálkozó összefüggések felfedezésére irányuló kedvet kifejleszteni. Annak ellenére mondom ezt, hogy tudom: a későbbi fizikatanulmányok során nem egyszer a jóga-gyakorlatok önfegyelmével kell majd a megszokott szemléletünket "kicselezni", megkerülni. De úgy tűnik, az idegrendszernek ahhoz, hogy több lépésből álló elvont gondolatmeneteket járhasson végig, elsősorban. éppen arra a biztonságérzetre van szüksége, amit a közvetlen benyomások körében való tájékozódó képesség nyújt.
A közvetlen tapasztalatra való sűrű támaszkodásért azzal kell fizetni, hogy az összefüggések nem lesznek átfogó érvényűek. Példa: fontos és hasznos felismertetni a gyerekkel, hogy ha egyszer a föld (a sár) nem átlátszó, akkor a sárral bevert szélvédő üvegen sem lehet keresztüllátni. De ez nem túl messzemenő összefüggés. Arról viszont a klasszikus fizikában úgyszólván semmit sem tudunk mondani, hogy a tölgyfaajtó és az ablaküveg közül miért az utóbbi az átlátszó, és arról sem, hogy ha az ablaküveg átengedi a fényt, akkor miért nem engedi át a futball-labdát is.
A modern fizika ezzel szemben mélyen. a közvetlenül érzékelhető "felszín" mögé lát, olyan alapvető építőköveket, fogalmakat és törvényszerűségeket tár fal, amelyek a korábbinál sokkal átfogóbb megértéshez vezetnek. A modern fizika meg tudja mondani, hogy miért a vas mágnesezhető és nem a réz, miért az üveg átlátszó és nem a fa. Éppen a modern tudomány jelentősége teszi megbocsáthatóvá azt az ötletet, hogy a megismertetés terhét egyenletesebben osszuk el az iskolaévekre és az izgalmas modern alapfogalmak közül néhányat már az általános iskolában bemutassunk. Az ötlet megbocsátható, de nem keresztülvihető. Nem lehet ugyanis "egy kicsit" bepillantani a felszín mögé, hanem csak kiadósan vagy sehogy.
Hadd érzékeltessem ezt a fény példájánál maradva. Hogyan lehetséges az, hogy a fény átmegy az ablaküvegen? Miért nem akad el benne, vagy miért nem töri össze? Ha ezt a kérdést egyáltalán felvetjük (oda akarok kilyukadni, hogy az általános iskolában jobb, ha nem vetjük fel), kézenfekvő feleletként csak az kínálkozik, hogy a fény "ártalmatlan" hullámjelenség. Valóban, a szomszéd lakásból a veszekedés "szépen" áthallatszik a falon, az északi oldalon a Balaton hullámai a nádason keresztül is elérik a partot. De ha a dolog ilyen egyszerű lenne, akkor mivel magyarázhatnánk, hogy nyár elején, néhány órával az első meggondolatlan napozás után, bőrünk égni kezd? A felhólyagzott bőr tanúsága szerint a napsugár inkább parányi lándzsások hadserege, mint ártalmatlan hullám. Milyen hát a fény valójában? Melyik hasonlat a helyes? Egyik sem, a fény sem a hullámzó Balatonhoz, sem a rohamozó sereghez nem hasonlít igazán. Éppen ez a magyarázata annak, hogy hol az egyik, hol a másik hasonlat jut az eszünkbe. (Képzeljük el, hogy egy idegen csillagról idelátogató űrhajós, aki feltehetően semmilyen földi élőlénynek nem hasonmása, egy röpke pillanatra láthatóvá teszi magát. Az lenne a csoda, ha utána a szemtanúk beszámolói nem mondanának ellent egymásnak.)
Természetesen nem arról van szó, hogy a modern fizika nem tudja világosan megfogalmazni, hogy ismereteink mai szintjén mik a fény alapvető jellemvonásai. Nagyon is meg tudja, de elvont, matematikai ízű fogalmak segítségével, amelyeknek pontosan az az érdemük (s egyben ez elvontságuk oka is), hogy egymástól látszólag távoleső körülmények között egyformán beválnak. A gyermeki szemlélet számára széteső dolgoknak (felégés és átlátszóság) az összekapcsolása azonban olyan érdem, amit egy 12 éves gyerek nem képes méltányolni. A sokféleséget egyszerre célbavevő és mégis ellentmondásmentes magyarázat igényéből született fogalmakat a 12 éves gyerek legfeljebb úgy értheti meg, hogy tökéletesen hamis tartalommal tölti meg őket.
Sőt próbáljunk meg őszintén lenni önmagunkhoz. Mire a középiskolás korig eljutunk, már kialakul bennünk s felnőtt korunkat is végig kíséri a logikai ellentmondás-mentesség igénye. Ettől az igénytől hajtva át tudjuk érezni, hogy ha a modern fizika - mondjuk - a hol hullámként, hol részecskék rajaként viselkedő fény jellemzésére átfogó érvényű fogalmakat talált, akkor ezeknek a fogalmaknak elvontaknak és egyben erőteljeseknek kell lenniök. A változatos felszín mögött felfedezett egység nem elszegényedést, hanem gazdagságot jelent, mint ahogy csali igazi tehetséggel tud egy színész egymástól elütő szerepeket egyaránt jól eljátszani. Alighanem ennek a gazdagságnak az élménnyé, közkinccsé tétele a természettudományos nevelés legvalódibb értelme. A szóbanforgó elvont, matematikai ízű fogalmak szabatos, részletekbe menő ismerete azonban nem feladata a tanártársadalomnak, még kevésbé a társadalom egészének, és nem is szükséges a modern világkép átéléséhez. Az utóbbihoz elegendő a középiskolában megizmosodó logikai igény és az ellentmondások izgalma, feltéve, hogy az általános iskolában a gyereket a jelenségek megfigyelésére és a természet szeretetére tanítottuk meg.
Lépjünk most közelebb tulajdonképpeni témánkhoz. Még mindig nem a gravitációról lesz szó, hanem az elektromos és mágneses mezőről.
A mezőfogalom általános iskolai bevezetését az a vélemény sugallta, hogy az üres téren keresztül ható kölcsönhatás (a mágnes úgy rántja magához a vasszöget, hogy előzőleg nem ér hozzá) helyén kezdettől fogva a kontakt-kölcsönhatásnak, a mágnest a vassal, az elektromosan töltött testeket egymással összekötő anyagi hídnak kell szerepelnie.
Nos, való igaz, hogy pl. az elektromosan töltött testet körülvevő elektromos mezőt - a didaktikai nehézségeket most figyelmen kívül hagyva - jogosan tekinthetjük folytonos anyagnak. Azt, hogy a tér valamelyik pontjában van-e jelen elektromos mező, helyi méréssel megállapíthatjuk, nem szükséges átkutatnunk a távolabbi környezetet elektromos töltések után. Elég, ha a kérdéses pontba egy atomot helyezünk. Elektromos mező hatására, az atom eltorzul, deformálódik. Az atomot felépítő ellentétes töltésű részecskéket ugyanis az elektromos mező egymással ellentétes irányban igyekszik elmozdítani. (Közvetve ez a hatás magyarázza meg azt is, hogy a búzadara az elektromos erővonalak mentén rendeződik. A dararészecskék polarizálódnak - két végükön ellentétes töltések jelennek meg - majd a szomszédos dararészecskék ellentétes töltésű végei egymáshoz tapadnak.) A pontról pontra való kimutathatóság az, ami az elektromos (vagy mágneses) mezőt viszonylag kézzelfoghatóvá, anyagivá teszi. (És elsősorban a pontról pontra való kimutathatóság az, ami, mint nyomban meglátjuk, nem teljesül a gravitációs mező esetében.)
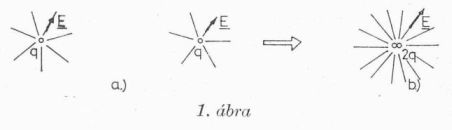
Az elektromos mező anyagisága azonban korántsem annyira szemléletes valami, amennyire a mező szó sugallja. Ha két virágcserép földet összeöntünk, az együttes földmennyiség se kevesebb, se több nem lesz, mint amennyi volt. De nézzük meg, mi történik, ha két egyforma, pozitív, kezdetben távoli töltést egymás mellé hozunk!
Legelső észrevételünk az, hogy a "Mennyi elektromos mező van itt?" kérdésre eleve nem kínálkozik olyan könnyű válasz, mint a "Mennyi föld van ebben a cserépben?" kérdésre. Ezen a nehézségen azonban úrrá lehetünk. A "mező sűrűségének" a mező energiasűrűségét tekinthetjük, ezt egy arányossági tényezőtől eltekintve az E elektromos térerősség négyzete adja meg. A töltésektől távolodva a térerősség gyorsan csökken, ezért a kiindulási helyzetben ott, ahol az egyik töltés által létesített térerősség még számottevő, a másodiktól származó térerősség elhanyagolható és viszont. Így a kezdőhelyzetben a mező összenergiája nyilvánvalóan a kétszerese az egyetlen q körüli energiának. Az összetolás után a 2q töltés körül bármelyik pontban a térerősség a kétszerese, a térerősség négyzete pedig négyszerese annak, ami az egyedülálló g-tól ugyanekkora távolságban uralkodna, most tehát a mező összenergiája a magános q körüli energia négyszerese. Nyugodtan mondhatjuk, hogy a töltések közelítése közben az elektromos mező gyarapszik. Természetesen a mező energiája nem "magától" nő, a különbözetet az a munka fedezi, amelyet végeznünk kell, miközben az egynemű töltéseket egymáshoz közelítjük. A köznapi tapasztalatok körében azonban a "közönséges" anyag mennyiségét nem lehet munkavégzéssel megváltoztatni. A kása nem lesz több attól, hogy kavarjuk.
Így hát, még ha a gravitáció bonyodalmaival nem kelleme is számolnunk, attól félek, hogy amit a távolhatás elleni hadakozás közben a réven nyerünk, azt elveszítjük a vámon. Az elektromos mező olyan anyagi híd, ami megbírja a műegyetemet, de a 12 éves gyerekek alatt leszakad.
Térjünk rá a gravitációra. Gravitációs mező az elektromos mezővel analóg jelentéssel, tehát mint a testeket körülvevő folytonos anyag, a tudomány mai állása szerint nem létezik és ilyenfajta elképzelés a múltban sem uralkodott. A klasszikus fizika a gravitációt, tudatosan vagy hallgatólagosan, távolhatásként kezeli, akkor is, ha az elektromos mezőben már anyagsűrűséget lát. Ettől még ne tartsák ezt a megjegyzést cinikusnak - nyugodtan megengedhetnénk az általános iskolában azt a kegyes csalást, hogy az egyszerűség és egységesség érdekében a gravitációs mezőt is folytonos anyagként mutassuk be. Csakhogy az analógiával már az általános iskolai megfigyelőképesség szintjén is baj van: a "gravitációs mező erővonalait" semmiféle búzadarával vagy vasreszelékkel nem tudjuk láthatóvá tenni. (Ennek, mint nyomban meglátjuk, alapos oka van.) A gimnáziumban pedig kifejezetten arra kényszerülnénk, hogy a csalást leleplezzük.
Képzeljük ugyanis magunk elé az előbbi elektrosztatikai példa gravitációs megfelelőjét, tehát két egyforma tömeget, először távol, azután összehozva.
Ha jogos lenne a gravitációs mezőt az elektromos mező mintájára elképzelni, akkor nyilván most is azt kellene mondanunk, hogy a két tömeg összehozásától a gravitációs mező energiája megnőtt (kezdetben az egyetlen tömeghez tartozó energia kétszerese volt, végül a négyszerese lett). Az elektromos esetben indokolt is volt az energianövekedés, hiszen az egymást taszító egynemű töltések összekényszerítésénél kívülről munkát végeztünk a rendszeren. A két tömeg azonban vonzza egymást, közeledésük közben mi nyerhetünk munkát a rendszerből - meg is tesszük, így működnek a vízierőművek. Hogyan nőhetett volna közben a mező energiája? Az elektromos mezővel való analógia látnivalóan nem lehet túl szoros.
Minthogy a nehézkedés modern fizikai értelmezése egészen biztosan túlságosan elvont ahhoz, hogy az iskolai tananyagban való szerepeltetése szóba jöjjön, semmi más utat nem látok, mint azt, hogy a gravitációt a hagyományos módon, a testek egymásra gyakorolt vonzásaként mutassuk be, egyáltalán nem firtatva azt a kérdést, hogy ezt a hatást mi közvetíti. Ehhez hadd tegyem hozzá, hogy ha egyszer a kontakt-kölcsönhatás központba állításáról lemondunk, akkor az elektromos és mágneses jelenségek körében is megszabadulunk attól a kényszertől, hogy a valóban elvégezhető megfigyeléseket a mező élményt adni még nem tudó, elvont fogalmával terheljük meg.
Vizsgáljuk most meg, hogy a gravitációs hatás miért nem tekinthető anyagi hídnak két test között.
Röviden azért nem, mert gravitációs mező (gravitációs térerősség) jelenlétét a tér valamelyik pontjában helyi méréssel kimutatni lehetetlen. Emlékezzünk vissza: ha egy atomot elektromos mezőbe helyezünk, az atom eltorzul, deformálódik. De ha egy téglát kézbeveszünk, ráhelyezünk egy másikat, majd a kettőt egyszerre elengedjük, esés közben se nem nyomják egymást, se el nem távolodnak egymástól. Manapság, az űrhajózás korában, különösen könnyű a gravitációnak ezt a rejtélyes tulajdonságát érzékeltetni. A Föld körül keringő, hajtóművét nem működtető űrhajóban pontosan ugyanolyan lebegésszerű, zavartalan állapot - a súlytalanság állapota - uralkodik, mintha a Föld nem is lenne a közelben. Az űrhajós csak onnan tudja, hogy merre van a Föld, hogy látja az űrkabin ablakán keresztül. A Föld felszínén, a mindennapi életben, amikor pl. egy nehéz zsákot cipelünk, úgy tűnik a számunkra, hogy a gravitációs erő jelenlétét közvetlenül érezzük. (Erre még visszatérünk.) De azért "idelenn" is elgondolkodhatunk azon a furcsaságon, hogy ha egy test a gravitációs erőnek nem szegül ellene, akkor a gravitáció mindennemű hatása a test belső állapotára semmivé lesz. Ha egy műugró a torony peremébe kapaszkodva függ, érzi a saját súlyát, izmai feszülnek. Ha "ellenállását" feladja, akkor arra a néhány másodpercre, amíg a vízbe ér, belső állapota a műholdak űrhajósainak feszülésmentes állapotával válik azonossá. (Összehasonlításul: a karóránk akkor is tönkre megy, ha csak keresztül esik is egy erős mágneses mezőn.)
A klasszikus fizika azzal a megállapítással tért napirendre e furcsaság fölött, hogy a testeknek a gravitációs erőkért felelős, ún. súlyos tömege és a tehetetlen tömege egymással arányos. Pl. a Föld annál nagyobb erővel vonz egy követ, minél nagyobb a kő tehetetlen tömege. Így azután a szabadesés gyorsulása minden testre nézve ugyanakkora. Minthogy a newtoni elmélet a gravitációt távolhatásként kezeli, némi csodálkozás után belenyugszik abba, hogy az űrhajó műszerei semmiféle jelét nem mutatják annak, hogy az űrhajó valamiféle "erőlevesen" haladna keresztül. A newtoni gravitációelmélet ma is tanítható jó közelítés.
A súlyos és tehetetlen tömeg arányosságának igazi jelentőségét azonban Einstein ismerte fel, aki erre a tapasztalatra építve a gravitáció jelenségének mélyreható s a további tapasztalatok által megerősített értelmezését adta meg. A részletekhez bonyolult matematika szükséges, az alapgondolat azonban néhány mondattal megvilágítható.
Előkészületként oldjuk meg a következő "április elsejei" feladatot. Rajzoljunk egy létrát - már rajzolom is - amelynek a szárai egymással párhuzamosan egyenesek, a fokai szintén egyenesek, amelyek merőlegesek a két szárra és a baloldali száron d távolságban követik egymást - de úgy, hogy a jobboldali száron a szomszédos létrafokok távolsága ne d legyen, hanem annál kisebb, vagy nagyobb!
Rövid töprengés után valószínűleg bárki megesküszik rá, hogy ezt a feladatot lehetetlen megoldani. Pedig hát igenis lehetséges ilyen létrát rajzolni, csak nem síkra, hanem például egy tejesüveg felületére, így:
"Hohó!" - mondják a kedves kartársak. "Csakhogy ezek a vonalak itt nem igazi egyenesek!". Valóban, ezek a vonalak nem euklideszi egyenesek. De nem nehéz belátni, hogy az üveg felületén ezek a vonalak ugyanúgy "tovább nem egyenesíthető" vonalak, mint a síkon a közönséges egyenesek. Szabálytalanabb, kacskaringósabb vonalakat könnyen rajzolhatunk az üvegre, de "szebbeket", simábbakat nem. Tanulság: az alapul választott felülettől függ, hogy a rárajzolt legsimább (legegyenesebb) vonalaknak milyen lesz a természetrajza, az egymáshoz való viszonya.
Egyszerűség kedvéért eddig felületekről beszéltünk. A tér, amelyben élünk, háromdimenziós, és C. F. Gauss, a matematikusok fejedelme, már a múltszázad első felében felvetette azt a gondolatot, hogy azok a fizikailag realizált vonalak - kifeszített kötelek, a fénysugár útja stb. - amelyekről általában azt képzeljük, hogy az euklideszi geometria elvont egyeneseinek gyakorlati megvalósításai, esetleg nem engedelmeskednek pontosan az euklideszi geometria axiomáinak. Gauss kísérleteket is végzett, megmérte egy olyan háromszögben, amelynek oldalai fénysugarak voltak, a szögek összegét, de az akkori mérés pontosság mellett nem talált eltérést a 180 foktól. A klasszikus fizika a magukra hagyott testek pályáiról is azt tételezte fel, hogy azok euklideszi egyenesek.
Térjünk most vissza az űrhajóban uralkodó súlytalansági állapothoz, amely nem árulja el, hogy van-e égitest a közelben. Einstein radikális következtetése szerint amit lehetetlen kimutatni, az nincs is. Gravitációs mező nem létezik, a szabadon eső liftben, vagy a Föld körül keringő űrhajóban nem csupán ugyanolyan, hanem ugyanaz az állapot áll fenn, mint a tömegektől távol lebegő űrhajóban: a zavartalanság. A fékezetlenül zuhanó lift vagy a keringő űrhajó mozgása szabad (erőmentes) mozgás. (A szabadesés kifejezés tehát ösztönösen a lényegre tapint rá.)
Dehát egyszerűen le akarjuk tagadni a gravitáció jelenségét? Szó sincs róla! A modern fizika csupán a vonzóerőt száműzi, a tömegek hatását nem. A tömegeknek van szerepe, de nem az, hogy folytonos anyagot (mezőt) keltenek, hanem, hogy megváltoztatják maguk körül a szabad mozgások egymáshoz való viszonyát, a pályák által tükrözött geometriai tartalmat. Emlékezzünk vissza: a tejesüvegen a létrát alkotó vonalak a legsimábbak, amilyeneket az üvegre egyáltalán rajzolni lehet, a létra mégis torz. Azt mondjuk: azért, mert a tejesüveg görbült felület. Ugyanúgy: a modern fizika a nagy tömegek közelében létrejövő mozgást a lehető legsimább mozgásnak tekinti, csakhogy nem euklideszi, hanem a tömegek által begörbített térben. Nem ördöngősség a dolog. (Csak véletlenül azt ne higyjék, hogy ezt kell tanítani!) Torz létrát a síkra is lehet rajzolni, persze csak görbe vonalakkal. Bizonyos mértékig egykutya, hogy egy ábra azért torz, mert bár síkra rajzoltam, de csúnya vonalakkal, vagy azért mert a legsimább vonalakat használtam, de egy csúnya felületen. A nagy tömegek közelében az űrhajók, vagy elhajított kövek viselkedése elbonyolódik a tömegektől távoli viselkedéshez képest, ezt mutatja a tapasztalat. A newtoni felfogásban a, tömeg közvetlenül a mozgást "csúnyítja", a modern fizika szerint a teret, amely a lehető legsimább mozgás színpadául szolgál. A két felfogás között a közvetlen szemlélet nem illetékes választani: a newtoni távolhatás "mechanizmusát" éppen úgy nem látjuk a lelki szemeinkkel, mint a görbült teret. Matematikai és kísérleti finomságok egyértelműen mutatják, hogy a geometriai felfogás a mélyrehatóbb. A részletekbe nem mehetünk bele, csak egy szót hadd szóljak a súlyról, itt a föld felszínén. A trambulin szélén álló sportolóra a klasszikus felfogás szerint két erő hat. A Föld tömege húzza lefelé, a deszka nyomja felfelé. A modern fizika szerint a szabadon eső sportolóra nem hat erő (nem is érzi, hogy hatna), a nyomába lépő, még az ugródeszkán álló kollegájára viszont egy erő hat, s ezt érzi is: a deszka nyomja felfelé. Egymáshoz képest tehát a két sportoló gyorsul.
Befejezésül: használhatjuk-e ezekután a "gravitációs mező" kifejezést? Nyugodtan! Teljes általánosságban azt a térséget érthetjük rajta, amelyben a tömegek hatása érvényesül.
________________________
Az ELTE Oktatási Szakcsoportja által az általános iskolai fizikatanárok részére szervezett előadás. Azért közöljük, mert, némi poétikus elemet látunk abban, hogy éppen Einstein születésének századik évfordulóján érnek el az ő gravitációra vonatkozó gondolatai az iskola kapujáig.
Végtelenül tanulságos ebből a szempontból egy nemrégen elvégzett csimpánz kísérlet. A kísérleti "személynek" levetítenek egy filmet, amelyen egy ember valamilyen problémával, pl. magasra akasztott banán megszerzésével (hasztalanul) küszködik. Utána két fényképet tesznek a csimpánz elé, ezek közül az egyik olyan tárgyat vagy mozdulatot ábrázol, amelynek segítségével az előbbi probléma megoldható. A csimpánz (az ilyen típusú kísérletek körülményeihez való megfelelő szoktatás után) ki tudja választani a helyes képet! Úgy látszik tehát, hogy a környező tárgyak "logikájának" a megértése előfeltétele az összetettebb gondolkodásnak.