Fizikai Szemle honlap |
Tartalomjegyzék |
Radnai Gyula
ELTE Általános Fizikai Tanszék
Az elektromágneses hullámok tanítása máig nyitott kérdése a fizika módszertanának.
Feynman Nobel díjas fizikus előadásában őszintén és nyíltan beszél a nehézségekről:
"Semmiféle olyan képet nem tudtam alkotni magamnak az elektromágneses térről, amit akárcsak megközelítően is pontosnak mondhatnék. Régóta foglalkozom az elektromágneses térrel, és negyed századdal ezelőtt éppen olyan helyzetben voltam, mint Önök, akik éppen most ismerkednek a vibráló hullámokkal. Amikor a térben tovahaladó mágneses erőtér tárgyalásakor az E és B vektorokról beszélek, lengetem a karomat, és Önök azt hiszik, hogy amit mondok, azt mind látom is magam előtt. Nos, amit 25 esztendős tapasztalat birtokában látok, az mindössze a következő: Elmosódott, bizonytalan, homályos, tekervényes, vibráló vonalak, némelyikre itt-ott, egy-egy E vagy B betű van írva, és talán egyes vonalak nyíllal is el vannak látva; igen közelről szemlélve a képet a nyilak eltűnnek. Amikor tovasuhanó erőterekről beszélek, képzeletemben szörnyű összevisszaságban keverednek a valóságos objektumok és az ezek leírására alkalmazott szimbólumok ... Nem képzelhetem magam elé a tovaszáguldó erővonalak kicsiny kötegeit, mert az nyugtalanít, hogy ezek egyszer csak eltűnnek; ha más sebességgel haladok. Márcsak azért sem látom mindig az elektromágneses teret, mert olykor arra gondolok, hogy a vektor és skalárpotenciállal kellett volna képet alkotnom, mert talán ezek vibrálása fizikailag lényegesebb fogalom ..." [1].
Mit tehet ma az elektromágneses hullámokat tanító középiskolai tanár az iskolában, ha szeretné megismertetni diákjait a XIX. század fizikájának egyik nagy teljesítményével, azzal, amire a XX. század technikájának olyan fejezetei épülnek, mint a rádiózás, televíziózás, űrtávközlés technikája?
Alapjában véve két különböző megközelítésre van lehetősége: a történetire és az elemi fizikaira.
A történeti megközelítés értéke, hogy a tanár a fizikai fogalmak fejlődését követheti végig úgy, ahogy az a valóságban történt. Felhasználhatja a történeti szemléletű tanítás számos előnyét: a tudósokat, mint embereket mutathatja be, s a sorsukat meghatározó társadalmi viszonyokat a tudomány fejlődésével való kölcsönhatásban tárgyalhatja. Nemcsak a sikereket, hanem a kudarcokat is felidézheti, így adhat reális képet magáról a történeti fejlődésről. A történeti út példája és tanulságai bátorítják a tanulókat a tévedésekkel szembeni megértő magatartás kialakítására, a töretlen fejlődés hamis illúziójának feladására, egyéni kudarcaik jobb elviselésére, saját munkájuk reálisabb értékelésére.
Az elemi fizikai megközelítés értéke viszont a bemutatott út egyszerűsége, érthetősége. A fizikai lényeget emelheti ki a tanár, s ez minél egyszerűbben sikerül, annál meggyőzőbb a diákok számára. Viszonylag kevés fogalommal dolgozhat, az új fogalmakat pedig egyszerűen tudja bevezetni. A jó tanár körültekintően választ ki speciális eseteket, szándékosan vesz elő fantáziát megmozgató analógiákat, modelleket. Ezzel a diák önbizalmát növeli, azt a kívánatos érzését erősíti, hogy ő is képes rájönni a dolgokra, hogy érti és használni tudja ezt a fizikát.
A tanárnak nem kell egyszer s mindenkorra eldöntenie, hogy tanításában a történeti, vagy az elemi fizikai megközelítésből induljon-e ki. Egyéniségétől, tanítványainak beállítottságától s a tanított témától függően választhatja hol az egyiket, hol a másikat. A legfontosabb témáknál valószínűleg mindkettőre sort kerít, hiszen tanításának alapelve az, hogy ha lényegeset, fontosat akar tanítani, akkor ezt érdekesen és egyszerűen kell tennie.
1792-ben Claude Chappe francia feltaláló mutatta be a francia nemzetgyűlésnek az első karjelzős távírót. A találmányt elfogadták, 70 km hosszú vonalat létesítettek, összesen 22 állomással. Egy-egy állomáson levő torony tetején karokkal felszerelt hosszú rúd állt. A karokat a toronyszobából zsinórokkal mozgatták, a jeleket a szomszéd állomásról távcsővel figyelték. A karok különböző kombinációjából 196 féle jelet lehetett adni. Németországban 1794-ben nyitották meg az első Chappe-távíróvonalat, Angliában Londont a kikötőkkel kötötték össze ilyen rendszerű távíróval.
125 évvel később, 1917-ben pedig már csupán New York közelében mintegy 500 amatőr rádióállomás működött, s akkor már több mint 15 éve megvalósult a rádióhullámokkal közvetített távíróösszeköttetés Európa és Amerika között, az Atlanti óceán felett.
Az elektromágneses hullámok felfedezése, a tudományos elmélet kialakulása párhuzamosan haladt a távközlés technikájának fejlődésével.
Tekintsük át röviden, kronológiai vázlatszerűen az elektromágneses hullámok fizikájának és technikájának
történetét [2, 3, 4, 5].
1791: Galvani, az akkor már 55 éves anatómiaprofesszor a bolognai egyetemen egy tudományos
közleményt publikál munkatársai és saját megfigyeléseiről. Ebben közli nevezetes békacomb kísérletét és
megpróbál magyarázatot is adni a jelenségre, amelyet, állati elektromosságnak nevez el. Hosszú
évek során tudatos kísérletezéssel gyűjtött tapasztalatokról számol be, melyek közül csupán a legelső volt
véletlen felfedezés, a többi a jelenséget céltudatosan vizsgáló kísérletező eredménye. Azért nem publikálta
előbb, mert teljesen új, addig ismeretlen jelenségcsoportra bukkant. Többek között két olyan tapasztalatról
is beszámol, amelyet az elektromágneses hullámok első tudományos megfigyelésének is
tekinthetünk. Az egyik: a boncolókés alatt a békacomb akkor rándult össze, amikor a teremben
működtetett elektromos megosztógépen éppen szikra ütött át. A másik: ugyancsak gyakran összerándult
egy rézhorog segítségével az ablak vasrácsára akasztott békacomb, ha zivataros idő volt és gyakran villámlott.
Galvanit és az akkor még fiatal honfitársát, Voltát azonban sokkal inkább érdekelte a megfigyelt hatást közvetlenül kiváltó elektromosság természete, mint az a távoli ok, amely ezt az elektromosságot működésbe hozta. Volta nem értett egyet Galvani magyarázatával: elvileg más okot keresett, amelyet ő a különböző anyagok érintkezésében vélt megtalálni, s ezért az egész jelenségcsoportot érintkezési elektromosságnak nevezte el.
Ma már tudjuk, hogy bizonyos fokig mindkettőjüknek igaza volt. A kor azonban Volta elméletére volt érett, s a tudomány fejlődését éppen az vitte akkor előre, hogy Volta, saját igazának bizonyítására céltudatosan keresett és talált olyan nem állati eredetű anyagokat, amelyeket felváltva egymás után illesztve az első komolyabb áramot szolgáltató telepet tudta megvalósítani.
Galvaninak nemcsak a XX. század biofizikája szolgáltatott igazságot, hanem már Volta is, igaz a maga módján. Galvani néhány év múlva meghalt, Volta pedig róla nevezte el az első egyenáramot adó telepet galvánelemnek. Galvani neve mind a mai napig él a "galvanizálás" kifejezésben, valamint a vezetékek közvetlen érintkezését jelölő "galvanikus csatolás" kifejezésben. Az utókorra maradt tehát a jelenségek Volta féle magyarázata Galvani nevével fémjelezve. (Vajon hány XX. századi felfedezésről fognak hasonló megállapítást tenni a XXI. században?)
1821: A 30 éves Faraday Angliában felfedezi a mágnes-áram kölcsönhatást.
1822: A 47 éves Ampére Franciaországban a dán Oersted kísérleteit továbbfejlesztve körültekintő, átgondolt kísérletsorozat eredményéképp felfedezi az áram-áram kölcsönhatást és a tömegvonzás newtoni elméletéhez hasonló átfogó elmélettel kívánja ezt magyarázni.
1831: egyik határkő az elektromágneses hullámok felfedezéséhez vezető úton: Faraday 40 éves korában felfedezi az indukció-törvényt. Itt a kísérlet mindenképp megelőzi az elméletet. Faraday saját szemléletes elgondolása a következő években, az anyagok fontos tulajdonságainak felfedezése közben, ezen felfedezések hatása alatt alakul, kristályosodik ki. Faraday 46 éves korában fedezi fel a szigetelők dielektrikusságát, 53 éves korában az anyagok diamágnességét. Ezek után természetesnek tűnik számára, hogy a vákuumot is elektromos tulajdonságokkal ruházza fel, ezért vezeti be a tér "elektrotonikus" állapotának fogalmát. Kísérleti fizikus lévén nem is akarja szemléletes modelljét matematikai formába öltöztetni, és nem is befolyásolják a közben Európában erőteljesen fejlődő távolhatás elméletek. Már 65 éves, amikor egy fiatal skót fizikus megadja a "Faraday erővonalak" első matematikai elméletét. A tudomány szerencséjére ez az akkor 25 éves fizikus Maxwell, aki még 10 évig tudományos levelezést folytat Faradayvel, miközben egyre tisztábban tűnik elő az elektrodinamika új elmélete. Maxwell írja Faradayről:
"Talán a tudomány előnyére szolgált az a tény, hogy Faraday, ámbár a tér, idő, erő alapvető formáinak teljes ismeretével rendelkezett, nem volt hivatásosan képzett matematikus ... Így aztán zavartalanul végezhette munkáját, hangolhatta össze elképzeléseit a tényekkel, és fejezhette ki azokat természetes, mesterkéletlen nyelven ... Faraday lelki szemeivel az egész teret átívelő erővonalakat látott ott, ahol a matematikusok távolbaható erőközpontokat láttak; Faraday közeget látott ott, ahol ők semmi mást, mint távolságot láttak; Faraday a jelenségek lényegét a közegben végbemenő tényleges hatásokban kereste, míg amazok megelégedtek azzal, hogy megtalálták azt valamilyen távolbaható erőben ..." [2].
A természettudomány nyelve, a matematika a XIX. század elején sokkal fejlettebb volt, mint a természettudomány maga, nem is beszélve az akkor még rendkívül alacsony technikai színvonalról. Lássunk erre néhány példát.
1807: Fourier publikálja a rezgések felbontásának elméletét.
1812: Csak ekkor jelenik meg az első elektromos távíró, amely galvánelemekkel és elektrolitos érzékelőkkel működik. Minden egyes galvánelemtől külön fémhuzal vezet egy-egy elektrolittal telt kémcsőbe. Amikor a telepet bekapcsolják, az elektrolitban gázfejlődés indul meg. Az első távíró öt független vezetékkel működik.
1822: Megjelenik Fourier könyve, amelyben részletesen kidolgozza a hővezetés matematikai elméletét. Ebben a hőt mint egyfajta anyagot, fluidumot kezeli. A termodinamika tanítása mind a mai napig szenved attól, hogy Fourier korrekt és magas színvonalú matematikai tárgyalása évtizedekkel megelőzte a hő szabatos és tiszta fogalmának kialakulását a fizikában. Fourier munkássága viszont rendkívül nagy hatással volt harminc év múlva arra a William Thomsonra, aki a távvezetékekben terjedő elektromos rezgések elméletét Fourier hővezetéselméletének analógiájára dolgozta ki. Róla még később több szót ejtünk.
1830: Az első próbálkozás a vezetékben terjedő elektromos jel sebességének mérésére Wheatstone nevéhez fűződik. Két egymás mellett elhelyezett szikraközön üttetett át szikrát. A két szikraközt 13 km hosszú vezeték kötötte össze, az egyikre kapcsolta rá közvetlenül azt a feszültséget, amin a szikra átütött. Mivel az elektromos jel terjedéséhez a 13 km hosszú úton bizonyos időre volt szükség, ezért a második szikraközben a szikrakisülés bizonyos időkéséssel követte az elsőt. A késési időt úgy mérte, hogy forgótükörrel húzta szét az egymás melletti két szikrakisülés képét, s a két kép egymástól való eltávolodását mérte. A jel terjedési sebességére a fénysebesség másfélszeresét kapta. A mérés hibáját valószínűleg az okozta, hogy a 13 km hosszú huzalt Wheatstone saját kertjében felállított oszlopok köré tekerte fel, s így tulajdonképpen egy nagy tekercset kapott, amelynek jelentős induktivitása lett. Wheatstone mentségére szolgáljon, hogy csak egy évvel később fedezte fel Faraday az indukció jelenségét. Ez pedig valóban mérföldkő volt az elektromosságtan fejlődésében. Alig két évvel Faraday felfedezése után:
1833: Göttingában a csillagászati intézet vezetője az akkor 56 éves Gauss, és a fizikai intézet vezetője az akkor 29 éves Weber, 1,5 km hosszú egyvezetékes távírót létesítenek a két intézet között. Ez a távíró egyfajta fizikai demonstrációs kísérlet az indukcióra: az elektromos jelet, amely a vezetékben fut, indukcióval keltik, ezért elég egyetlen vezeték.
1837: Stephenson megbízásából Wheatstone megépíti az első elektromos rendszerű vasúti távírót Londonban, két egymástól 3 km távolságra levő állomás között. Az öt mágnestűs érzékelővel dolgozó távíró higanyérintkezős hívókészülékkel működött. Később Wheatstone kéttűs érzékelőre egyszerűsítette a berendezést. Az információtovábbítás logikai sémája nagyon hasonlít a későbbi Morse kódrendszerre.
1840: Az Egyesült Államokban egy ötvenéves festőművész - bizonyos Samuel Morse - szabadalmaztatja elektromos távíróját.
1842: Egy 18 éves diák, aki egy éve a cambridgei egyetem hallgatója - neve William Thomson, - az elektromos rezgésekről publikál egy tudományos dolgozatot. Ebben Fourier munkáira támaszkodva lefekteti a vezetékben terjedő elektromos rezgés - a kábelhullám elméletének alapját. A dolgozatra alig figyelnek fel, Thomson maga hívja fel rá a figyelmet, amikor később egy hasonló jellegű munka elvégzésére kérik fel.
1846: Weber publikálja azt a távolhatás elméletet, amely két töltés közti erőhatást a töltések helyzetének, sebességének és gyorsulásának függvényeként írja le. Ezzel egyetlen formula speciális eseteként tárgyalható a nyugvó töltések közti erőhatás, valamint a mozgó töltések által képviselt áramok közti erőhatás. A gyorsuló töltések között még külön erő is fellép. Újra fontossá vált a fény sebességének minél pontosabb mérése. Franciaországban 1849-ben Fizeau és néhány hónappal később Foucault egymástól különböző módszerekkel az alábbi értékeket mérték a vákuumbeli fénysebességre:
1849: Fizeau: 314 ezer km/s.
1850: Foucault: 298 ezer km/s.
Fizeau és Foucault egy évben születtek, 30-31 évesek voltak akkor, amikor ezeket a méréseket végezték.
1850: az első tengeralatti kábel lefektetésének éve. A kábel Calais és Dover között húzódik, ez az első közvetlen távíróösszeköttetés Anglia és a kontinens között. Gazdasági jelentősége óriási. Vállalkozások alakulnak az Európa és Amerika közötti tengeralatti távírókábel lefektetésére. A munka tudományos irányítására később Thomsont kérik fel.
1852-55 között Weber és Kohlrausch egyre pontosabban mérik meg az elektromágneses (áramból adódó) és elektrosztatikus töltésegység hányadosát, mely a mérési hibán belül megegyezik a fénysebesség mért értékével.
1856: Maxwell cikke a Faraday erővonalak matematikai elméletéről.
1857: Első sikertelen próbálkozások az atlanti kábel lefektetésére.
1862: Maxwell, aki időközben a kinetikus gázelmélet kidolgozásán fáradozott, újra visszatér az elektromágneses tér dinamikus elméletéhez.
Rendkívüli intuícióval, mechanikai analógiákból kiindulva bevezeti az eltolási áram fogalmát. Újabb három év telik el megfeszített szellemi munkával, amelynek eredménye egy újabb fontos cikk:
1865: Maxvell 34 éves korában publikálja a fénysebességgel terjedő elektromágneses hullám elméletét.
1866: végre siker koronázza az atlanti kábel lefektetésének 10 éves munkáját. A siker kulcsa egy Great Eastern nevű óriáshajó, melyet eredetileg az Európából Ausztráliába kivándorlók számára építettek. Befogadóképességét 6000 utas vagy 10000 katona( !) számára tervezték. A vállalkozás csődbe jutott, a Great Eastern mégis nagy szolgálatot tett a technika fejlődésének: 1866 júliusában két hét alatt lefektették segítségével az összesen mintegy 5000 tonnányi kábelt. A munka szellemi és gyakorlati irányítója a Great Eastern fedélzetén utazó Thomson volt. Amikor tudományos munkásságáért később elnyerte a Lord címet, ezért született többek között az a javaslat, hogy a Lord Cable címet kapja. (A cable szó kábelt és táviratot is jelent.) Ő azonban egykori skót szülővárosa egyik kis folyójának nevét választotta, s így lett neve Lord Kelvin. (Egy bizarr gondolat: kevés hiányzott ahhoz, hogy ma az S I rendszer kötelező bevezetése idején Európában 1 Kábel legyen az abszolút hőmérséklet mértékegysége ...)
1867: Faraday meghal. Maxwell most már egyedül dolgozik tovább elektrodinamikai elméletén. A Weber-Kohlrausch mérés eredményét Maxwell elmélete értelmezni, magyarázni tudja, ez a kísérlet akkor az egyetlen tapasztalati érv Maxwell elmélete mellett. Ezért Maxwell megismétli a kísérletet, és saját mérései megerősítik Weber és Kohlrausch mérésének eredményét. Újabb öt év telik el, amíg Maxwell megírja az elméletet összefoglaló munkáját.
1873: megjelenik a Treatise. Maxwell könyve nehéz olvasmány. Nem csoda, ha a kortárs fizikusok körében kevés visszhangot vált ki. A newtoni távolhatás gondolata, amelyet Ampere majd Weber fejlesztett tovább az elektromos jelenségek leírására, a korabeli fizikus-matematikus-tudós tekintélyek számára rokonszenvesebbnek, elfogadhatóbbnak tűnt. Hagyományosan tudományosabbnak. Maxwell csak a legfiatalabb tehetségek támogatására számíthatott, akik megértik Faraday szemléletét és Maxwell matematikáját. Két év sem telt el a Treatise megjelenésétől fogva, és megjelent egy sokat ígérő fiatal tehetség dolgozata.
1875: a 22 éves Lorentz levezeti a Maxwell elméletből az optika legfontosabb törvényeit, többek között a Fresnel formulákat és a Brewster törvényt.
1879-ben 48 éves korában meghal Maxwell.
Az elektromágneses hullámok elméletének diadala pedig csak ez után kezdődik.
1884: Poynting kiegészíti az elektromágnesség dinamikai elméletét az energiaáramlás elméletével.
1886: Hertz kísérletileg is kimutatja a szabad elektromágneses hullámokat. A kísérletek tudományos bizonyító értéke óriási, talán éppen ez tereli el Hertz figyelmét arról, hogy a jelenség gyakorlati hasznosíthatóságával is foglalkozzék. Helyette tankönyvírásba fog: nagy pedagógiai érzékkel és világos, tiszta stílusban megírja az elektromágneses tér Maxwell elméletét tárgyaló tankönyvét.
1890-ben jelenik meg a 33 éves Hertz tankönyve, s ebben a Maxwell egyenletek, lényegében a mai differenciális formában. Maxwell nehezen érthető jelölései után ez a könyv üdítő olvasmány, átütő sikert arat. Közben Lorentz következetesen dolgozik az eredeti Faraday koncepció továbbfejlesztésén. Fiatalkori sikere egész életpályáját meghatározta: mind több és több effektust sikerül megjósolnia, értelmeznie. Talán a szükségesnél is tovább viszi Faraday térelméletét: bevezeti, használja és terjeszti az éter fogalmát. Ennek hullámaiként értelmezi az elektromágneses hullámokat. (A rádióhullámokat ma is gyakran az éter hullámainak nevezik.)
1891: Lorentz publikálja éterelméletét, bevezeti az elektromágneses erőhatásra azóta róla elnevezett formulát.
1900: Lorentz és Poincaré bevezetik a térimpulzus fogalmát.
1904: Lorentz megadja annak a speciális transzformációnak egyik alakját, amellyel szemben a Maxwell egyenletek invariánsok.
S mi történt közben a technikában? Hogyan haladt előre a szabad elektromágneses-hullámok felhasználása távközlésben? Nézzük időrendben a technika fejlődésének legfontosabb állomásait.
1875: Bell (28 éves) feltalálja a telefont.
1879: Edison (32 éves) feltalálja az izzólámpát.
1895: Popov (36 éves) Petrográdban 1-2 km távolságú rádióösszeköttetést létesít először a szárazföldön, azután hajók között.
1896: Marconi (22 éves) bemutatót tart Londonban az elektromágneses hullámokkal történő hírtovábbításra.
1899: Marconi (25 .éves) rádiókapcsolatot létesít a La Manche csatornán át Calais és Dover között.
1901: Marconi (27 éves) kísérletet tesz Európa és Amerika közötti rádiókapcsolat létrehozására. A kísérlet sikerében csak amatőr fantaszták, hozzánemértők, megszállott vállalkozók hisznek. A fizikusok okosan azzal érvelnek, hogy a kísérlet ugyanaz, mintha egy 1 cm átmérőjű acélgolyó egyik oldalán felvillanó pontból kiinduló fénynek kellene az acélgolyó másik oldalát megvilágítania. Marconi mégis megpróbálja e kísérletet. És elsőre sikerül. Amire a fizikusok nem gondoltak: az adóból kiinduló rádióhullámokat a Földet körülvevő ionoszféra visszaveri, sőt még fokuszálja is. A bátorság és a szerencse véletlen(?) találkozása évtizedekkel gyorsította meg a technika fejlődését.
Maxwell elmélete valóban diadalt aratott. Olyat, amilyenre talán maga Maxwell se számított. Pedig ami a tudományos fejlődést illeti, ebben Maxwell jó jósnak bizonyult. Ezt mondta:
Abból az anyagból, amit mi Faradayvel összegyűjtöttünk, egy olyan új tudomány fog kialakulni, aminek mi még a nevét se ismerjük, s az a tudós, aki ezt majd felállítja, talán még meg se született.
1905: Einstein felállítja a speciális relativitás elméletét. Einstein ekkor 26 éves. Abban az évben született, amikor Maxwell meghalt.
Az egyetemeken, főiskolákon és a gimnáziumokban az elektromos és mágneses jelenségek tárgyalásában lényegében azt az utat követjük, amit a XIX. század közepéig járt be a fizika tudománya (elektrosztatika; magnetosztatika; egyenáram; elektrolízis; áram-mágnes, áram-áram kölcsönhatás; indukció). A sztatikus, majd stacionárius jelenségek tárgyalása után kerül sor a kvázistacionárius jelenségekre, azonban egyáltalán nincs szó az elektromos állapot kialakulásáról, terjedéséről. Ahelyett, hogy a felépítést logikusan folytatnánk és a vezetékben terjedő elektromos állapot leírására irányítanánk a figyelmet, átugrunk egy fél évszázadot a történeti úton, és azonnal a szabad elektromágneses hullámok tárgyalására térünk át.
Az egyetemen és a középiskolában lényegesen különböző az a matematikai nyelv, amivel a fizikai törvényeket meg lehet fogalmazni, ezért az elektromágneses hullámok tárgyalása a történeti út félretétele után az egyetemen és a középiskolában eltérő didaktikai módon valósul meg.
Az egyetemen általában követett módszer:
Induktív, tapasztalati úton, speciális törvények felfedezése és általánosítása útján eljutunk a Maxwell egyenletek integrális alakjához, amelyek vákuumra és S I rendszerben felírva a következők:
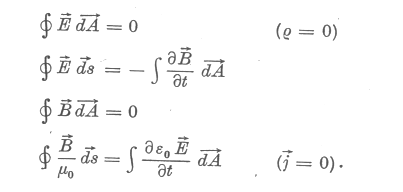
Az integrális alakról matematikai úton differenciális alakra térhetünk át. Így a következő egyenletrendszerhez jutunk, amelyet most kétféle jelölésmóddal is felírunk [10], [8].
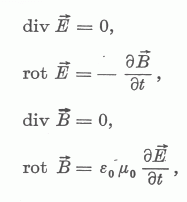
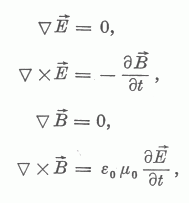
Képezzük a második egyenlet mindkét oldalának rotációját:
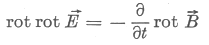
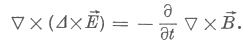
Helyettesítsük be a jobb oldalra rot 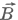 -t a negyedik egyenletből:
-t a negyedik egyenletből:

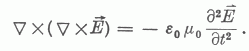
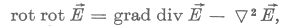
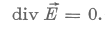
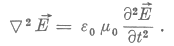
Hasonló alakú hullámegyenletet kaphatunk a mágneses indukcióvektorra is.
A hullámegyenletből leolvasható a hullám terjedési sebessége:
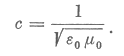
Középiskolában már a kvázistacionárius jelenségek tárgyalása is csak speciális harmonikus esetre és meglehetősen felszínesen, a matematikai módszerek erőszakolt egyszerűsítésével oldható csak meg. A tanulók szemléletében nem alakulhat ki az elektromágneses tér képe, csak az egymástól elkülönítve létező elektromos és mágneses téré. Az előbbi egy kondenzátor, az utóbbi egy tekercs belsejére koncentrálódik. Ebből a sztatikus térfogalomból szeretnénk, ha kialakulna a tanulók fejében az elektromágneses tér egységes, dinamikus képe. Milyen módszert kínál erre a középiskolai fizikametodika?
Egy igazi huszárvágással - didaktikai trükkel - szokás megoldani a gordiuszi csomót: kinyitjuk a rezgőkör kondenzátorát. Századunk akármelyik fizikatankönyvét lapozzuk fel: ismerősen köszön vissza az a 4-5 fázisból álló ábrasorozat, amelyik a rezgőkörrel kezdődik és az antennával fejeződik be.
A középiskolás számára, aki a megértés igényével közeledik a jelenségek fizikai magyarázata felé, ez az ábrasorozat csak egyet illusztrálhat: hogyan csúszik ki a talaj az értelmes,
gondolkodó tanuló lába alól. Előzőleg megértette és megtanulta a kondenzátort az elektromos térrel, a tekercset a mágneses térrel, s most végül talál egy darab drótot,
ami egyik se és mind a kettő egyszerre. Ráadásul egymásba gyűrűszerűen kapcsolódó elektromos és mágneses erővonalak táguló rendszerét kell elképzelnie egészen a végtelenig.
Akinek jó térszemlélete van, még el is tudja képzelni. Ezzel a képpel pedig nemcsak az a baj, hogy a tanuló nem tudja hozzákötni az elektromos és mágneses térhez addig
kialakított elképzeléshez, hanem legalább olyan baj, hogy alapvetően hamis: úgy tűnik, hogy az elektromágneses haladó hullámban az
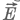 és
és 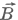 vektorok negyedperiódus fáziskéséssel követik ("keltik") egymást, holott
az elektromágneses haladó hullámban valójában E és B azonos fázisban vannak!
vektorok negyedperiódus fáziskéséssel követik ("keltik") egymást, holott
az elektromágneses haladó hullámban valójában E és B azonos fázisban vannak!
Az egyetemi oktatásban is hiánypótló, a középiskolai fizikatanításban pedig nélkülözhetetlen a szabad elektromágneses hullámok tárgyalását előkészíteni az elektromos állapot terjedésének vizsgálatával. Erre nagyszerű módszert kínál Thomson eredeti gondolatmenete a kábelhullámok tárgyalására. A továbbiakban elemi fizikai megközelítésben elvégezzük a kettősvezeték mentén terjedő elektromágneses hullám tárgyalását. A már mondottakon kívül ez az alábbi didaktikai előnyökkel jár:
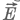 és
és 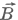 hullámtulajdonsága.
hullámtulajdonsága.
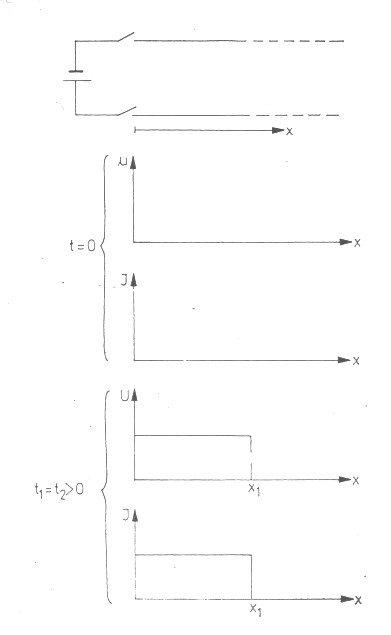
1. ábra. a) Végtelen hosszú kettősvezeték, amelyre a t = 0 pillanatban egy telepet kapcsolunk, b) a kezdő állapot grafikonja,
c) feszültség és árameloszlás a
kettősvezeték mentén valamely t1 > 0 pillanatban
Tekintsünk két párhuzamos egyenes fémhuzalból álló vezetékpárt, nevezzük ezt kettős vezetéknek. Legyen a kettősvezeték elég hosszú ("végtelen hosszú") a két huzal közti távolsághoz képest.
Kapcsoljunk a kettősvezeték egyik végére egy telepet a t = 0 pillanatban (1a. ábra). Vizsgáljuk, hogyan terjed a vezetékek közti feszültségállapot a kettősvezeték hossza mentén, az idő függvényében (1b. ábra). Hasonlóképpen vizsgálhatjuk az áramállapot terjedését is (1c. ábra).
Az állapot terjedésének fogalma már a mechanikából ismert - ott előkészített - fogalom. Felidézhetjük, mint jó analógiát a rugalmas rúdon terjedő deformáció, a lökéshullám esetét, melyet elemi fizikai meggondolásokban egymáshoz kapcsolódó m tömegű testek és D állandójú rugók láncolatán vizsgálhattunk meg (2. ábra). Elemi

2. ábra. m tömegű testek közé kapcsolt D direkciós állandójú rugók végtelen lineáris lánca
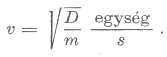
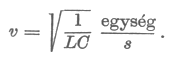
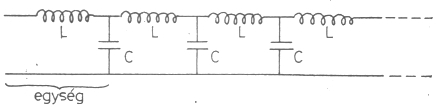
3. ábra. Ideális tekercsekből és kondenzátorokból
felépülő végtelen lánc
Azt várjuk, hogy a kettősvezetékben terjedő elektromos állapot is valami olyan sebességgel halad, ami a vezeték elektromos adataitól függ.
Talán ha a kettősvezeték hosszegységre eső kapacitását és induktivitását értelmezni tudnánk, előbbre jutnánk. Ennek érdekében válasszunk egy olyan kettős vezetéket, amely nem huzalokból, hanem két párhuzamos szalagból áll ! Ha itt sikerül értelmezni a kapacitást és az induktivitást, akkor a tanulók már valószínűleg el tudják képzelni, hogy más geometriájú kettős vezetékeknek, például a koaxiális kábelnek is beszélhetünk a hosszegységre eső kapacitásáról és induktivitásáról [5].
A kettősvezeték saját ohmos ellenállásától eltekintünk. Ebben az esetben a telepből állandó I áram folyik a vezetékbe, miközben a vezeték egyre hosszabb része töltődik fel a telep feszültségére.
Legyen a telep feszültsége U, a lemezekben folyó áram I. Jelöljük a lemezek szélességét a-val, egymástól való távolságukat d-vel (4. ábra).
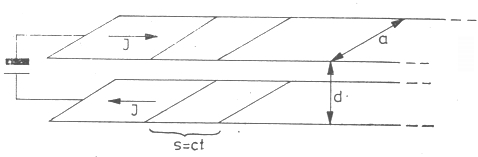
4. ábra. Párhuzamos lemezekből álló végtelen hosszú kettősvezeték, melynek
bármely
kiválasztott s hosszúságú darabja olyan síkkondenzátornak tekinthető,
amely
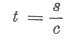 | idő alatt töltődik fel |
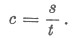
A t idő alatt a lemezekre felvitt töltés:
Q = It
Másrészt:Q = CU,
ahol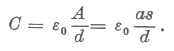
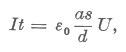
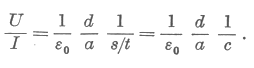
Az előbb a lemezpár s hosszúságú darabját sikkondenzátorként kezeltük, ami t idő alatt töltődött fel. Most ugyanezt az s hosszúságú darabot tekintsük egymenetes tekercsnek, amelyben az áram t idő alatt változik meg 0-ról I-re. A tanár számára itt jó alkalom kínálkozik az eltolási áram [6] természetes bevezetésére: csak úgy modellezhetjük a jelenséget tekercsben körben folyó árammal, ha feltételezzük, hogy a lemezekben folyó I árammal azonos nagyságú eltolási áram folyik a lemezek között (5. ábra).
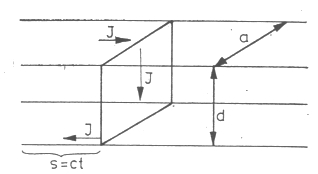
5. ábra. A párhuzamos lemezekből álló kettősvezeték kiválasztott s hosszúságú darabja olyan egymenetes tekercs egy darabjának tekinthető, amelyben a
lemezeken folyó vezetési áramot az eltolási áram egészítheti ki zárt körré. A "tekercs" tengelye párhuzamos a lemezekkel és merőleges az elektromos állapot
terjedésének irányára.
Az egymenetes, téglalap keresztmetszetű tekercs induktivitását határozzuk meg a szolenoidra megismert formula alkalmazásával:
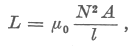
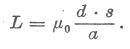
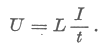
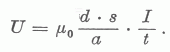
| Ebből fejezzük ki az | 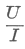 | hányadost: |
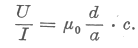
| Vessük ezt össze az | 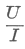 | előbb kapott értékével. A két egyenlőség egyidejűleg csak akkor állhat fenn, ha |
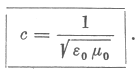
| További érdekes eredményhez jutunk, ha a | 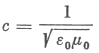 | formulát visszahelyettesítjük az |
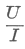 | hányadosra kapott |
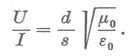
| Felhasználva µ0 és ε0 konkrét értékeit [6], [10], nemcsak a | 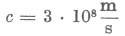 | fénysebességet kaphatjuk meg, hanem a |
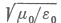 hányadost is meghatározhatjuk, amelyre
hányadost is meghatározhatjuk, amelyre
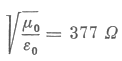
| adódik. Az | 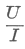 | hányadost a kettősvezeték "hullámellenállásának" nevezzük, amire most tehát ezt kaptuk: |
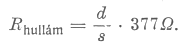
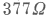 előtti tényező lesz más, a
kettősvezeték keresztmetszetének geometriájától függően.
előtti tényező lesz más, a
kettősvezeték keresztmetszetének geometriájától függően.
Mi a hullámellenállás fizikai jelentése?
Zárjuk le a kettősvezetéket egy éppen akkora ohmos ellenállással, amekkora a hullámellenállás értéke. Ebben az esetben az elektromos jel által szállított energia az ohmos ellenálláson teljesen disszipálódik, az együtt haladó feszültség és áramhullám nem verődik vissza.
A részletes meggondolások azt mutatják [10], hogy ha a kettősvezeték vége nyitott, akkor a feszültséghullám azonos fázissal, az áramhullám pedig ellenkező fázissal verődik vissza a nyitott végről.
Kapcsoljunk a kettősvezetékre a telep helyett egy olyan generátort, amelynek a feszültsége időben szinuszosan változik! Ekkor a kettősvezeték hosszától függően állóhullámok alakulhatnak ki. Mivel visszaverődéskor az áramnak van fázisugrása, a feszültségnek viszont nincs, ezért a kialakuló állóhullám olyan lesz, hogy a nyitott végén az áramnak csomópontja, a feszültségnek duzzadóhelye lesz. A kettősvezeték mentén a feszültség állóhullámnak mindig ott lesz csomópontja, ahol az áram állóhullámnak duzzadó helye van és fordítva.
Ha a kettősvezeték végét rövidre zárjuk, akkor az áramnak van duzzadóhelye és a feszültségnek csomópontja a zárt végen. Ebben az esetben is egymástól negyed hullámhossznyira találjuk felváltva a feszültség és áram duzzadóhelyeit.
Az egész jelenségkör szépen demonstrálható az ún. Lecher drótpárral [6]. A feszültség maximumokat glimmlámpával, az árammaximumokat zsebizzóval tudjuk megkeresni úgy, hogy a foglalatból vezető két érintkezőt végigcsúsztatjuk a kettősvezetéken.
Ha a kettősvezetéket a hullámellenállással megegyező értékű ellenállással zárjuk le, akkor nem kapunk állóhullámot, amint ez szintén demonstrálható. Nem kell tehát "végtelen hosszú" kettősvezeték ahhoz, hogy az egymással fázisban haladó feszültség és áramhullámot visszaverődésmentesen előállíthassuk.
Talán egy érdekes gyakorlati alkalmazást érdemes kiemelni, éppen iskolai fontossága miatt. Egyre több középiskolában épült már ki zártláncú televíziós rendszer. Itt az elektromos nagyfrekvenciás jelek továbbítása koxiális kábelen át történik. Fontos, hogy azokat a kábelvégeket, amelyek nem csatlakoznak üzemelő monitorhoz, a kábel hullámellenállásával megegyező értékű (leggyakrabban 75 ohmos) ohmikus ellenállással zárjuk le, mert különben a kábel végéről visszaverődő jel eljut az üzemelő monitorokhoz, s ott zavaró szellemképet, szerencsétlen esetben a kép teljes szétesését is okozhatja.
3.2. A kettősvezeték mentén kialakuló elektromágneses tér
Kísérletezzünk tovább a Lecher drótpárral! Állítsunk be egy jellegzetes állóhullámképet, amelyben a feszültség illetve árammaximumok a glimm, illetve az izzólámpával a már említett módon jól kimutathatók. Ezután fektessünk rá egy hálózati fénycsövet hosszában a drótpárra. A tanulókat megdöbbenti, amit látni fognak. A hosszú fénycső begyullad, világít, de nem egyenletesen, hanem szakaszosan. Legerősebben a fénycső azon helyek környezetében világít, ahol az előbb a feszültségmaximumokat találtuk. A fénycső a világításhoz szükséges energiát magából a térből veszi fel, mivel a drótpárral semmilyen fémes érintkezésben nem áll. Ezután vegyük el a fénycsövet és húzzuk végig a drótpár mentén egy olyan szigetelt vezetőből készített körvezetőt, amelyben egy zsebizzó van beiktatva. Újabb döbbenet: a kis izzó a körvezető mozgatása közben hol felgyullad, hol elalszik. Legjobban mindig ott ég, ahol az előbb árammaximumokat találtunk, s egyáltalán nem gyullad fel ott, ahol az áramcsomópontok voltak. Csakhogy az előbb az izzót fémesen kapcsoltuk a két vezetőhöz, most pedig semmi fémes érintkezés nincs a körvezető és a drótpár között! Ismét csak azt mondhatjuk, hogy a körvezető a térből vett fel energiát!
Kísérleti tapasztalatunk tehát az, hogy amikor a kettősvezetéken feszültség és áramhullám alakul ki, akkor a kettősvezeték mentén e térben elektromágneses hullám alakul ki!
A fellépő elektromágneses tér, a kialakuló elektromágneses hullám elemi fizikai tárgyalását ismét a két párhuzamos szalagból álló kettősvezetékre végezzük el. Ebben az esetben a két szalag közötti térben alakul ki és halad az elektromágneses hullám. A térjellemzők a következőképpen határozhatók meg:
1. Az 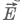 vektor a lemezek síkjára merőleges irányú, nagysága a síkkondenzátornál megismert összefüggés alapján:
vektor a lemezek síkjára merőleges irányú, nagysága a síkkondenzátornál megismert összefüggés alapján:
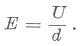
Amikor a kettősvezetéken feszültség állóhullám alakul ki, akkor a kettősvezeték menti térben az elektromos térerősségnek lesz állóhulláma. Ahol U amplitudója a legnagyobb, ott lesz a legnagyobb az E amplitudója. Így érthető a fénycsöves kísérlet: elegendően nagy elektromos térerősség olyan nagy sebességre tudja felgyorsítani a fénycsőben levő ionokat, hogy azok ütközéseik során gerjeszteni és gerjesztődni képesek. Az elektromos térből felvett energiát visszasugározzák, s a fénycső az ismert mechanizmussal világít.
2. A 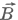 vektor a lemezek síkjával párhuzamosan az elképzelt egymenetű tekercs tengelyének irányába mutat.
Nagyságát az I áram és a kettősvezeték geometriája határozza meg. Alkalmazzuk a szoleonidra megismert formulát az egymenetű, téglalapkeresztmetszetű tekercsben
kialakuló
vektor a lemezek síkjával párhuzamosan az elképzelt egymenetű tekercs tengelyének irányába mutat.
Nagyságát az I áram és a kettősvezeték geometriája határozza meg. Alkalmazzuk a szoleonidra megismert formulát az egymenetű, téglalapkeresztmetszetű tekercsben
kialakuló 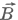 nagyságának kiszámítására:
nagyságának kiszámítására:
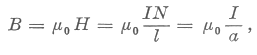
Amikor a kettősvezetéken áramállóhullám alakul ki, ekkor a kettősvezeték menti térben a mágneses indukció vektornak lesz állóhulláma. Ahol az I amplitudója a legnagyobb, ott lesz a legnagyobb a B amplitudója. Így válik érthetővé a körvezetős kísérlet. A nagyfrekvenciásan változó B a körvezetőben feszültséget indukál, ez a körvezetőben áramot indít, amely felizzítja a beiktatott zsebizzót.
3. Láttuk, hogy a kettősvezetéken a feszültség és az áramhullám egyidejűleg alakul ki. Elképzelhetetlen valamelyik is a másik nélkül. A kettő között éppen a hullámellenállás közvetítésével valósul meg a kapcsolat. Teljesen nyilvánvaló, hogy a kialakuló elektromágneses tér sem képzelhető el mint csak elektromos, vagy csak mágneses tér. Az is várható, hogy E és B ugyanúgy összefüggnek, ahogyan U és I összefüggött egymással.
| Próbáljuk meghatározni mindjárt az |
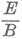 | hányadost! |
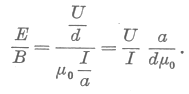
| Helyettesítsük be | 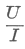 | helyére a hullámellenállás előbb kifejezett értékét! |
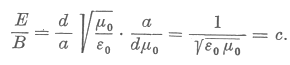
E = cB .
4. Megállapítottuk, hogy a két párhuzamos vezetőszalag között fénysebességgel haladó elektromágneses hullámban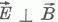 ,
és mindketten merőlegesek a terjedési irányra. A haladó hullámban
,
és mindketten merőlegesek a terjedési irányra. A haladó hullámban 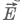 és
és
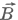 azonos fázisban vannak, s abszolút értékeik között a következő összefüggés áll fenn: E = cB
azonos fázisban vannak, s abszolút értékeik között a következő összefüggés áll fenn: E = cB
. Most vizsgáljuk meg az energetikai viszonyokat. Írjuk fel a térfogati energiasuruséget a kialakuló elektromágneses térre. Ehhez a síkkondenzátor elektromos és a szoleonid mágneses energiájának a középiskolában levezethető formuláit kell csak felhasználnunk.
A térfogat: s · a · d
| Elektromos energia: | 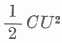
|
| A mágneses energia: | 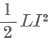
|
Tehát. az elektromágneses energiasűrűség:
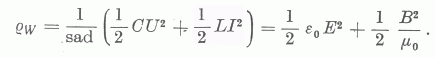
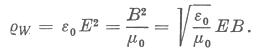
5. Határozzuk meg az energiaáramsűrűség nagyságát: Ez definíció szerint az energiasűrűség és a terjedési sebesség szorzata.
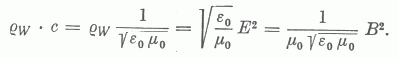
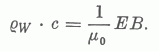
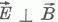 .
.
6. Határozzuk meg az elektromágneses tömegsűrűséget. Ez az Einstein féle E = mc2 összefüggés alapján:
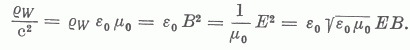
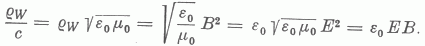
Láttuk, hogy a kettősvezeték mentén terjedő elektromágneses hullámra, hogyha az párhuzamos fémszalagok között terjed, elemi fizikai módszerekkel lehetett levezetni szinte minden olyan fontos összefüggést, amely a szabad elektromágneses hullámokra is igaz.
Az a kép, amelyet az elektromágneses térről a kettősvezeték modellje sugall, tartalmilag, fizikailag sokkal közelebb áll a szabad elektromágneses hullámokhoz, mint amint a rezgőkör "topológikus" átalakításával kaphatunk.
Mégis, befejezésül röviden vázolnunk kell, hogyan térjünk át a kettősvezeték mentén terjedő hullámról a szabad elektromágneses hullámokra. Két utat javaslunk, mindkettőnek az a lényege, hogy az eltolási áram szerepét fokozatosan növeljük, a vezetékben folyó áram rovására.
1. Kapcsoljunk a párhuzamos szalagokból álló kettősvezetékre olyan nagyfrekvenciás generátort, melynek frekvenciáját fokozatosan növelni tudjuk. Így a kettősvezetékbe képzelt egymenetű szoleonidnak egyre rövidebbre kell választanunk az s oldalhosszát. Végül is a kialakuló B már szinte kizárólag az eltolási áramtól függ. A hullám mintegy leszakad a határoló fémszalagokról, amelyek már csak a terjedés irányát tűzik ki.
2. Fokozatosan növeljük a két fémszalag egymástól való távolságát. Ezáltal ismét olyan helyzet áll elő, hogy az elképzelt szolenoidban az eltolási áram "hossza" nő a vezetékben folyó áram "hosszához" képest. Határesetben az egymástól végtelen messze távolított fémszalagok körülbelül olyan szerepet játszanak az elektromágneses hullámok terjedésében, mint amilyet a végtelenbe kivitt töltés játszik annak a sztatikus térnek a kialakításában, amit e töltés ittmaradt párja létesít.
A most javasolt elemi fizikai megközelítés olyan hézagpótló ötlet az elektromágneses hullámok tanításához, amely azért még számos kérdést nyitva hagy. Hogy csak a legfontosabbat említsük: nem tértünk ki a relativitáselmélet által felvetett sok problémára az elektromágneses tér hullámterjedésének szemléletes elképzelésével kapcsolatban.
Egyáltalán nem a megnyugtatás szándékával, inkább a kutatási kedv felcsigázására idézzük végül Feynman már idézett előadásából a Nobel díjas fizikus alábbi megállapítását:
"Az igazi hullámokat valójában nem tudom jól megközelíteni képszerű ábrázolással. Önök se nyugtalankodjanak tehát, ha nem boldogulnak egykönnyen a képalkotással - mások is ugyanilyen nehézségekkel küzdenek" [1].
[l ] R. P. Feynman, R. B. Leighton és M. Sands, Mai fizika, 8. köt., Műszaki Könyvkiadó, Budapest, 1970 p. 94.
[2] Simonyi Károly, A fizika kultúrtörténete, Gondolat, Budapest, 1978.
[3] Horváth Árpád, Korok, gépek, feltalálók, Gondolat, Budapest, 1966.
[4] Ifj. Gazda István és Sain Márton, Fizikatörténeti ABC, Tankönyvkiadó, Budapest, 1978.
[5] Nuffield A level Physics, Unit 8. The Nuffield Foundation, 1971.
[6] Budó Ágoston Kísérleti Fizika II. Tankönyvkiadó, Budapest, 1968.
[7] Nagy Károly, Elektrodinamika, Tankönyvkiadó, Budapest, 1968.
[8] R. P. Feynman, R. B. Leighton és M. Sands, Mai fizika 6. köt. Műszaki Kiadó, Budapest, 1970.
[9] Novobátzky Károly és Neugebauer Tibor, Elektrodinamika és optika, Tankönyvkiadó, Budapest 1951.
[10] Simonyi Károly, Elméleti villamosságtan, Tankönyvkiadó, Budapest, 1976.