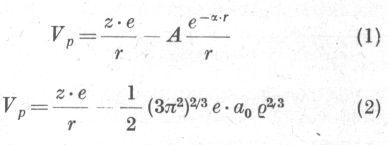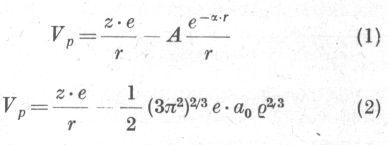Fizika Szemle 1984/12. 445.o.
PSZEUDOPOTENCIÁLOK ÉS SŰRŰSÉGFÜGGŐ ELMÉLETEK
Gáspár Rezső
Kossuth Lajos Tudományegyetem,
Elméleti Fizikai Intézei
A pszeudopotenciál egy olyan modelpotenciál, melynek tere a valencia elektronok mozgását meghatározza és így azok a törzs elektronokra való állandó figyelés nélkül vizsgálhatók.
1935-ben Gombás Pál és Hans Hellmann [1] egyidejűleg publikálták a pszeudopotenciál elvi gondolatát és annak alakjára két formát is felmutattak
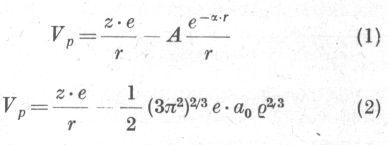
ahol z · e az ion törzs töltése (e az elemi töltés és a0 a legkisebb
Bohr sugár) ρ az ion törzs elektronjainak sűrűsége és r a magtól való távolság, A és α állandók.
Míg Hellmann-t a második világháború előszele eltüntette, Gombás és tanítványai igen aktív munkával feltárták a gondolatban rejlő lehetőségeket. Azóta a fejlődés az egész világ nevesebb kutató laboratóriumaiban szétterjedt és a gondolat igen termékenynek bizonyult.
A fejlődés legfontosabb lépései a következők voltak.
- A legeredetibb gondolat már az első cikkben meg volt, ti. hogy a valencia elektronok által meghatározott jelenségek (optikai spektrum, ionizáció, a kémiai kötés, a szilárd testek kötése és elektronszerkezete stb.) az iontörzs formális jelenléte nélkül is vizsgálhatók, ha a valenciaelektronok mozgását egy speciális potenciáltérben a pszeudopotenciál jelenlétében vizsgáljuk.
- A probléma tárgyalásának matematikai nehézsége csökken az által, hogy a függvénytér dimenziója, melyben a jelenséget vizsgáljuk, erősen redukálódik és a meghatározandó sajátértékek nagyságrendje is csökken, Gombás Pál és munkatársai Kónya Albert, Kozma Béla és Péter Gyula ezt már a negyvenes évek elején megállapították [2].
- Már igen korán kiderült, először a potenciál probléma esetére Fényes Imre, majd a Hartree-Fock probléma esetében Szépfalusy Péter kutatásai által, melyet később J. C. Phillips és L. Kleinman és L. Szász továbbfejlesztettek, hogy nagy pontossággal is megfogalmazható [3].
- Igen egyszerű alakú szemikvantitatív pszeudopotenciál modell fejleszthető ki a szilárd testek elektron szerkezetének [4] és kötésének tárgyalására. Különösen érdekesek ezen a téren Gombásnak és munkatársainak a fémek és ionkristályok kötésére vonatkozó alapvető vizsgálatai [5] és a Fermi felületre vonatkozó vizsgálatok Cambridge-ben V. Heine és munkatársai [6] által, valamint J. C. Phillips vegyület kristályok elektronszerkezetére a Bell Laboratóriumban [7] és W. Harrison fémek elektronszerkezetére vonatkozó vizsgálatai Kaliforniában [8].
- Nagy molekulák és atomaggregátumok tárgyalására alkalmas programok fejleszthetők ki a pszeudopotenciál segítségével. Ezek igen jól használhatók farmakológiai vizsgálatok céljából és véges nagyságú szilárd test darabokon felületi hatások vizsgálatára is [9].
Végül említsük meg a pszeudopotenciál vizsgálatoknak egy olyan területét, melyek az analitikus alakú pszeudopotenciálokkal kapcsolatosak. Az ezekben található paraméterek meghatározásának Gombás művésze volt. Néhány heti munkával tudott olyan paramétereket produkálni, melyek az akkori vizsgálatoknál igen jól megállták helyüket. Manapság, amikor modern elektronikus számítógépekkel tudjuk vizsgálni a problémát, tudjuk, hogy 10-4 relatív pontosság szükséges a megfelelő eredmények elérésére [10] és így tudjuk Gombás művészetét igazán értékelni.
Az Atom Statisztikus Elmélete [11] az a másik nagy tudományterület, melynek fejlődését Gombás Pál működése jelentősen előrevitte. Ennek az elméleti módszernek a pályára állítását olyan nevek fémjelzik, mint Thomas, Fermi, Dirac [12]. Új lendületet adott az elméletnek a korreláció figyelembevételével Gombás. A fent idézett összefoglaló munkája és könyve újabb kutatások százainak lett kiinduló pontjává.
Új lendületet vettek az ilyen irányú munkák Hohenberg és Kohn 1964-ben megjelent közleménye óta [13], melyben a szerzők kimutatják, hogy a módszer, mint sűrűségfüggő módszer a statisztikákra való hivatkozás nélkül is megalapozható.
A statisztikus atomelmélet manapság újabb fellendülő korszakát éli, amit olyan neves kutatók bekapcsolódása fémjelez, mint E. Teller, J. Schwinger és A. Rajagopal [14]. Ez az új lendület annál is inkább érthető, hiszen különleges körülmények (nagy nyomás, magas hőmérséklet stb.) között levő anyag életünkben döntő szerepet játszik (Föld; Nap és csillagok belseje, atom és hidrogén bomba és termonukleáris reakció) és ezek elméleti megértése ennek segítségül hívását is igényli.
IRODALOM
[1] P. Gombás, Zs. Physik, 94, 473, 1935; H. Hellmann, J. Chem. Phys., 3, 61, 1935 és Acta
Physicochimica URSS, 1, 913, 1935; P. Gombás Pseudopotentiale, Springer-Verlag, Wien, New York 1967.
[2] P. Gombás, Zs. Phys., 116, 184, 1940; Gy. Péter, Zs. Phys., 119, 713, 1942; B. Kozma
und A. Kónya, Zs. Phys., 118, 153, 1941. B. Kozma, Mat. és Fiz. Lapok 48, 351, 1941.
Budapest.
[3] I. Fényes, Csillagászati Lapok, Budapest 6, 49, 1943; Múzeumi Füzetek, Kolozsvár, 3, 14, 1945;
P. Szépfalusy, Acta Phys. Hing., 5, 325, 1955; ibid. 6, 273, 1956; J. C. Phillips és L. Kleinman Phys. Rev.
116, 287, 1959; L. Szász, Z. Naturforsch., 32a, 252, 1977; ibid. 32a, 829 1977.
[4] I. V. Abarenkov és V. Heine, Phil. Mag.; 12, 529, 1965; J. N. Bardsley, Case Studies in Atomic Physics 4,
299, 1974.
[5] P. Gombás, Zs. Physik 121, 523, 1943; lásd még R. G. Gordon és Y. S. Kim, J. Chem. Phys., 56, 3122, 1972.
[6] V. Heine, Solid State Physics, 24, 1, 1970; M. L. Cohen és V. Heine, ibid. 24, 38, 1970; V. Heine és
D. Weaire, ibid, 24, 250, 1970.
[7] J. C. Phillips Bonds and Bands in Semiconductors, Academic Press, New York, 1973.
[8] W. Harrison Pseudopotentials in the Theory of Metals, Benjamin, New York 1966.
[9] H. E. Popkie és J. J. Kaufman, Int. J. Quant. Chem., 10, 47, 1976.
[10] R. Gáspár, Int. J. Quant. Chem., 23, 1017, 1983.
[11] P. Gombás, Die statistische Theorie des Atoms und ihre Anwendungen, Springer, Wien, 1949 (megjelent magyar nyelven is).
Encyclopedia of Physics. Ed. S. Flügge, Vol 36, P. Gombás, Statistische Behandlung des Atoms, p. 109-232,
Springer Verlag, Berlin, 1956.
[12] Lásd [11]-et.
[13] P. Hohenberg és W. Kohn, Phys. Rev. B, 136, 864, 1964.
[14] B. G. Englert és J. Schwinger, Phys. Rev. A., 29, 2331, 2339, 2353, 1984; A. K. Rajagopal, Adv. Chem. Phys.,
41, 59, 1980; E. Teller, Rev. Mod. Phys., 34, 627, 1962.