KÖZELI CSILLAGOK BOLYGÓTÖMEGŰ KÍSÉRŐINEK KUTATÁSA

Bruce Campbell
Dominion Astrophysical Observatory
Herzberg Institute of Astrophysics
G.A.H. Walker, S. Yang
Department of Geophysics and Astronomy
University of British Columbia

1. Bevezetés

Egészen a legutóbbi időkig nem volt megvalósítható Naprendszeren kívüli bolygók keresése a csillagok látóirányú sebességének a mérésével, mivel a radiálsebesség mérések csak ritkán voltak pontosabbak 500 ms^-l-nál. Egy Jupiter-típusú bolygó hatására az anyacsillag pályamenti sebessége, amely legfeljebb néhányszor 10 ms^-1, nyilvánvalóan beleveszne a mérési hibába. A bolygószerű kísérők radiális sebességének a kimutatásához a pontosság egy-két nagyságrendű javítása szükséges.
Éppen ilyen mértékű növekedést értünk el a sebesség mérésében egy újonnan kifejlesztett technika segítségével. Ezt a technikát az elmúlt hat évben 16 csillag relatív sebességének a monitorizálására használtuk. A radiális sebességek mérési pontossága, és megfigyeléseinknek az időtartama, most már lehetővé teszi, hogy néhány előzetes megjegyzést tegyünk a Naphoz hasonló csillagok bolygótömegű kísérőinek előfordulási gyakoriságával kapcsolatban.

2. A hidrogén-fluorid abszorpciós cella technika

Ezt az új technikát eredetileg Campbell és Walker javasolta (1979). Egy hidrogén-fluorid gázt tartalmazó cellát helyeznek egy konvencionális coudé spektrográf rése elé. Mielőtt a cellán áthaladó csillagfény a spektrográfba lép, HF abszorpciós vonalak rakódnak rá. Ezek a vonalak olyan megbízható hullámhosszat jelentenek, amelyek nem mozdulnak el a csillag abszorpciós vonalaihoz képest a spektrográfban fellépő optikai effektusok miatt. Ez lényeges különbség a hagyományos technikához képest, amelynél külön fénynyalábot használnak a hullámhossz-kalibrációra szolgáló összehasonlító színkép előállítására. Ennél a hagyományos megközelítésnél nincs biztosíték arra, hogy mind a csillagból jövő, mind pedig az összehasonlító nyaláb a spektográfban ugyanazt az utat fussa be. Ennélfogva elkerülhetetlen eltérés van a csillag színképe és az összehasonlító színkép között, amely azután a sebességekben lényeges hibaként jelentkezik, különösképpen a legnagyobb felbontásoknál. Mindezeket a szisztematikus hibákat el lehet kerülni abszorpciós cella használatával.
Hidrogén-fluoridot választottunk erre a célra, minthogy a) mindössze 90 cm hosszú cella esetén már erős abszorpciós vonalakat kelt, b) a vonalak jól szétválnak, úgyhogy egy sor különálló csillag-vonal esik közéjük, c) és nincs egybeesés ritka izotópok gyenge vonalaival, illetve földi eredetű abszorpciós vonalakkal. Elővigyázatosnak kell lenni, mivel a HF mérgező gáz, személyi sérülést okozhat, és károsodást az optikai műszerekben, ennélfogva a cellát elővigyázatosan kell kezelni.
A HF cellával a megfigyeléseket a Mauna Kean-levő 3,6 m-es kanadai-francia-hawaii teleszkóppal végezték. A detektor Reticon fotodióda sor, amelynek elegendően nagy dinamikus tartománya van ahhoz, hogy nagy jel/zaj arányú, tipikusan 1000:1, színképek készíthetők vele. Ilyen kiváló minőségű színképen az egyes HF és csillagból származó abszorpciós vonalak helyzete kb. 0,2 mikron pontossággal határozható meg, amely a megfigyelt vonalak sokasága esetén kb. 10 ms^-1 sebesség pontosságának felel meg.
Az adatok kiértékelésének módját részletesen Campbell és munkatársai (1986), valamint Campbell és Walker (1987) írták le. Ez magába foglalja a HF, illetve a csillagból jövő (egymástól függetlenül észlelt) vonalak spektrális felosztással felváltva történő szétválasztását, és Fahlman és Glaspey (1973) különbségi módszerével a vonalpozíció mérését. A viszonylagos vonalpozíciókat korrigáltuk a vonalak átfedéséből és az instrumentális profil változásából adódó gyenge effektusokra. Ezek után a radiális sebességet a szokásos módon határoztuk meg, és korrigáltuk a Naprendszer baricentrumára Stumpff (1980) nagy pontosságú föld-pálya rutinjait használva. Megjegyzendő, hogy gondosan meg kell határozni minden észlelés tényleges idejét, amikor a baricentrumra korrigálunk, minthogy Hawaiiban a Föld felszínének a gyorsulása a forgás következtében 114 m s^-1 hr^-1. Ennélfogva meghatároztuk minden felvétel közepes idejét egy exponométerrel mérve a spektrográfba belépő fluxust. A kiértékelésben az utolsó lépés a sebességek éjszakáról éjszakára történő csekély nullpont vándorlásának a figyelembevétele. (Ilyen változásokat a spektrográf optikai sajátságainak a változása okozhat.) Ezt úgy valósítottuk meg, egy adott csillag esetén, hogy az összes többi csillagnak az azonos megfigyelési szakasz alatt mért sebességének az átlagát használtuk korrekció céljára. Ennél a lépésnél azt a tényt használtuk ki, hogy programcsillagjaink nagy része nem mutat tényleges rövid időtartamú sebességváltozásokat. Ennélfogva bármely hosszú idejű trendtől való eltérés (lásd később) használható a nullpontkorrekció meghatározására minden megfigyelési időszakra.

3. A radiálsebesség-görbék analízise

 3.1 A sebességváltozások ellenőrzése

Az 1. ábra a τ Cetinek, az egyik program csillagunknak, a tipikus sebességgörbéjét mutatja. Az ábrázolt pontokhoz feltüntetett hiba tipikusan 10-12 csillagvonalból kapott sebesség statisztikus hibája. Ez ennél fogva a mérés belső hibáját jelenti.

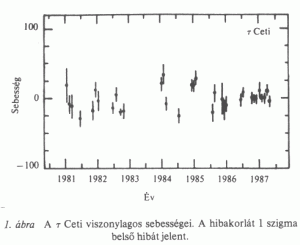
Ezeknek az adatoknak az alapján nyilvánvalóan nincs szignifikáns sebességváltozás néhány éves időskálán. A τ Ceti sebességének átlagos belső hibája 9,4 m s^-1, míg maguknak a sebességeknek a hibája (amelyet a továbbiakban külső hibának nevezünk) 13,9 ms ^-1 Úgy találtuk, hogy a belső és a külső hiba között nincs szignifikáns eltérés, és ennek alapján arra következtetésre jutottunk, hogy nincsenek 6 évnél rövidebb periódusú változások. Hasonlóan nem találtuk a jelét annak, hogy a többi csillag gyors változásokat mutatna.

Annak az objektív megbecslésére, hogy van-e a sebességekben hosszú idejû trend, az alábbi eljárást alkalmaztuk. Mindegyik adatsorhoz többszörös regressziós technikával egyenest, illetve parabolát illesztettünk. Ezek után meghatároztuk az adatok elsõ deriváltját (a meredekséget), illetve a másodikat (a görbületet) és a formális 1 szigma bizonytalanságát ezeknek az adatoknak, amely a külsõ hibák függvénye. A meredekség és görbület aránya a hozzájuk tartozó hibákhoz a hosszú idejû sebességváltozások szignifikanciájának a mértéke (|S|/σ_s illetve |C|/σ_c).

A 2. ábra a megfigyelt |S|/σ_s illetve |C|/σ_c  hisztogramját mutatja, 28 értéket 14 csillagra. (Két csillagot, a X¹ Orionist és a γ Cephei-t itt nem vettük tekintetbe, mivel nagy sebességváltozásuk valószínűleg csillagkísérőtől ered.) A 2. ábrán a folytonos vonal Monte Carlo-szimuláció eredménye 2000 sebességmintából. Mindegyik adatsor 27 pontot tartalmaz (ez a csillagonkénti megfigyeléseknek az átlagos száma és a sebességek eltérése a pontoktól éppen a sebességek tényleges szórása az összes csillag tekintetbe vételével mind a 27 megfigyelési szakaszban. Ennélfogva a szimulált adatok átlagosan a valódi csillagok viselkedését utánozzák, kivéve a sebességtrendet. A |S|/σ_s és |C|/σ_c eloszlása, amelyeket a véletlen adatokból határoztunk meg, nem meglepően, szigma = 1 szórású Gauss-eloszlás.

A 2. ábra megfigyelt eloszlása, ha összehasonlítjuk a szimulációkkal, szembeötlő többlettel rendelkezik 2,5 szigmaérték felett. 7 csillag esetén |S|/σ_c nagyobb, mint 2,5 és ezek a szignifikáns értékek az 1. táblázat második oszlopában találhatók. A szimulált eloszlásból a 28 esetből mindössze 0,6-ot jósolnánk, amelynél szigma nagyobb 2,5. Szembeötlően γ² Delphini rendelkezik a legkisebb szignifikanciával ebben a csoportban, ennélfogva változását nem tekintjük reálisnak. Ezzel szemben az ε Eridani (lásd 3. ábrát) és a ξ Bootis A > 4 szigma szinten szignifikáns, és ezért ezeket a "valószínű" változások osztályába soroljuk. A többi csillag esetében a változások szignifikánsak, de nem magas szinten, és így ezeket "lehetséges" változóknak osztályozzuk.

3.2 γ Cephei - hármas rendszer?

A 4. ábra felső része a γ Cephei K szubóriás sebességgörbéjét mutatja. A precíziós radiális sebesség mérés által kimutatott igen nyilvánvaló sebességváltozás láthatóan nem volt kimutatható hagyományos módszerekkel. Ezt a változást valószínűleg csillagkísérő okozza, és ezért ez az objektum nem különösebben érdekes.

Mindazonáltal a γ Cephei sebességgörbéjének a behatóbb vizsgálata azt mutatja, hogy az nem sima, hanem az általános trendre rakodó változásokra utal. Ezeknek a változásoknak a kimutatására levontuk a sebességekre illesztett másodrendű görbét, és az eredményül kapott maradékokat a 4. ábra alsó részén szemléltettük. Ez kismértékű-változást mutat, amelynek a periódusa 2,7 év és nagysága kb. 25 m s^-1. Mivel adataink kétszer olyan hosszú időszakot fednek le, mint ennek a változásnak a periódusa, úgy hisszük ez egy "valószínű" változó, és egy harmadik test is igen valószínűen jelen van a rendszerben. Azonban a harmadik test által okozott perturbációnak a pontosabb meghatározása a második test pályájának a pontosabb meghatározását igényli.

4. A kísérő tömegének a felső korlátja

Annak a céljából, hogy felső korlátot állapítsunk meg a programban szereplő csillagok lehetséges kísérőire, a fentebb meghatározott meredekségeket és görbületeket használhatjuk. Ezekre az 1 szigma felső határ egyszerűen S_max = |S| + σ_s és C_max = |C| + σ_c. Körpályát feltételezve meg lehet mutatni, hogy ezeknek a határoknak a segítségével a kísérő tömegére az alábbi összefüggést lehet kapni Jupiter-tömegekben a (P) periódusfüggvényében:

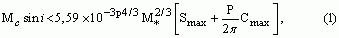
ahol M_* a főkomponens tömege napegységekben. Vegyük észre, hogy ez a határ egyenesen arányos a periódussal.

Egy további korlát kapható a régi parallaxis vizsgálatokból, amelyek Gatewood szerint (1986) α = 0,01 szögmásodpercnél nagyobb, láthatatlan kísérő által keltett perturbációt mutathatnak. Ebben az esetben ismét, kör alakú pályákat feltételezve, azt kapjuk, hogy

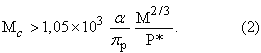
ahol π_p a parallaxis. Ez a határ fordítottan arányos a periódussal, és így az (1) és (2) egyenletek kombinációja a kísérő tömegére egy olyan felső korlátot ad, amely független a periódustól. Ezeket a korlátokat a 14 programcsillag esetén az 1. táblázat utolsó oszlopa tartalmazza. Megjegyzendő azonban, hogy 50 évnél nagyobb periódusú perturbációk a parallaxis vizsgálatokkal már nem mutathatók ki, így ezek a korlátok olyan kísérőkre vonatkoznak, amelyek 14 csillagászati egységnél közelebb vannak központi csillagukhoz. Hangsúlyozni kell, hogy ezek a határok egyenesen arányosak a csillagnak a Naptól mért távolságával,

amely igen tág határok között mozoghat. Ennek a felső korlátnak a középértéke 8 Jupiter-tömeg, amelyet ezeknek a csillagoknak a kísérőire felső korlátnak tekintünk.

Az 1. táblázatban annak a 7 csillagnak a kísérőjére kapott alsó korlátot is feltüntettük, amelyeket "lehetséges" vagy "valószínű" sebességváltozóknak osztályoztunk. Ezeket a határokat a megfigyelt sebességtartományokból vezettük le, amely nem lehet nagyobb, mint a sebesség amplitúdójának a kétszerese. A periódus alsó korlátja 12 év, kétszerese megfigyeléseink időtartamának, minthogy egyik változót sem észleltük a periódus felénél hosszabb ideig (az ε Eridani lehetséges kivételével). A γ Cephei esetében a tényleges periódusból és amplitúdóból kapott tömeg 1,7-szerese a Jupiterének.

5. Kísérő objektumok barna törpék, vagy bolygók?

Az meglehetősen világos, hogy programcsillagaink egyike sem rendelkezik a csillagokénál kisebb tömegű kísérővel a 10-80 Jupitertömegnyi barna törpe tartományban. Ez egybeesik több napjainkban végzett, a barna törpék felfedezésére irányuló vizsgálattal, amelyek mind a mai napig egyetlenegy esetet sem találtak. McCarthy, Probst, és Low (1985) bejelentése arról, hogy a Van Biesbrock 8 barna törpe kísérővel rendelkezik, nyilvánvalóan hibás. (Skrutskie, Forrest és Shure 1987; Perrier és Marioni 1987), Jameson, Sherrington és Giles (1983), Srutskie, Forrest és Shure (1986), valamint Kumar (1987) a közeli csillagok kísérőinek infravörös tartományban végzett kutatása nem mutatott ki a durván 40 Jupitertömegnél nagyobb kísérő jelenlétét. Az IRAS katalóguson Chester és munkatársai által (1986) végzett vizsgálat sem mutatott ki egyetlen barna törpe jelöltet sem. Marcy és munkatársai által végzett mérések során, amelyet egy 65 M törpéből álló minta kis amplitúdójú sebességváltozásának tanulmányozására végeztek, csak egy lehetséges barna törpe kísérőt eredményezett, de Marcy (1987) manapság úgy véli, hogy ez az objektum igen közel van ahhoz a határhoz, ahol a stabil hidrogénégés beindul. Összegezve, a rendelkezésre álló bizonyítékok jelenleg arra utalnak, hogy a barna törpék igen ritkák, vagy talán nem is léteznek. (Lehet, hogy ez szerencse, mert ha barna törpék léteznének nagy számban, akkor nagyon kevés stabil bolygórendszer lenne!)

Ha a "nagytömegű" barna törpék (10-80 Jupitertömeggel) ilyen ritkák, minek klasszifikáljuk azokat a kísérő objektumokat, amelyeket találtunk? A 15 eset közül 7-nél van 1-8 Jupitertömegű "lehetséges" vagy "valószínű" kisérő. Az igen kistömegű kisérők ilyen mértékű túlsúlya, összevetve a közepes tömegű objektumok hiányával, arra enged következtetni, hogy van egy űr a csillagokénál kisebb tömegű objektumok eloszlásábsn. Amennyiben ez az űr reális, akkor ez azt jelenti, hogy az általunk felfedezett objektumok a bolygótömeg-spektrum felső szélén vannak. És ha a 16 csillagnál talált 7 kísérő felfedezését a későbbi mérések megerősítik, akkor ez azt jelenti, hogy a naphoz hasonló csillagoknál a bolygórendszerrel rendelkezők aránya valószínűleg f_p ≥ 0,45.

__________________________