A TERMODINAMIKA MEGALAPOZÁSA

Tisza László
MIT, Boston

A termodinamika megalapozása a múlt században történt meg, elmondható tehát, hogy a termodinamika 19. századi tudomány. Miért érdekes számunkra ma?

A múlt században senki sem tudta, hogy léteznek-e atomok, és a fő érv a termodinamika mellett, a kinetikuselmélettel szemben, az volt, hogy nem használ kétes hipotéziseket. Feltehetjük a kérdést, hogy maradt-e még jelentősége ennek a tudománynak korunkban, amikor az egyedi atomokkal is könnyen kísérletezhetünk. Nyilvánvalóan, már az hogy beszélek róla, azt jelzi, hogy hiszek abban, hogy a termodinamikának még jelentős szerepe van.

Noha a kvantummechanika nagyon sikeresen írja le az atomok és más részecskék viselkedését, van olyan terület, ahol módszerei csak részlegesen megbízhatóak, és szükség van arra, hogy az empirikus analízis határt szabjon a spekulációnak. Tekintsük például azt a problémát, amit a fizikusok erős csatolásnak neveznek. A folyékony hélium például az erős csatolás elméletével írható le. Az atomok közötti kölcsönhatás nagyon erős, és nem lehet egyszerűen a Schrödinger egyenletből kihozni a megoldást. Ilyen esetekben mindenféle közelítést és szellemes feltételezést szokás alkalmazni. Nagyon érdekes, hogy a termodinamika határokat tud szabni, meg tudja mondani, hogy mi az, amit valóban tudunk, és hogy alkalmazhatjuk-e a feltételezéseinket. A termodinamika még mindig érdekes. Önöket feltehetően nem kell erről meggyőzni, hiszen azért jöttek, hogy termodinamikát hallgassanak.

Felmerül azonban a következő kérdés: A termodinamika törvényeit ugyanúgy fogalmazzuk-e meg, mint a múlt században? Vagy van-e valami igazi újdonság? Úgy gondolom, hogy van. Minden generációnak újra fel kell fedeznie a régi dolgokat. A szolgai ismétlés hanyatlásra vezet. Sorra fogom venni egyenként a termodinamika nulladik, első, második illetve harmadik főtételét, és megmutatom mi az, amit ma velük kapcsolatban másként mondanék. A fő hangsúlyt a harmadik főtételre és Nernst szerepére fogom fektetni. Nézzük tehát sorjában!

A nulladik főtételt fogalmazták meg explicite utoljára, de a kalorimetria megalapozói már a 18. században hallgatólag tudták, és használták. Először a második, majd az első, végül a harmadik főtételt fogalmazták meg. Ezután jutott valakinek az eszébe, hogy először azt kell rögzíteni, hogy a hőmérséklet létezik. Ezt az állítást nulladik főtételnek nevezzük [3].

A természetben egy általános törekvés van az egyensúly felé. Ezt kellene először kimondani. Ez messze túl mutat a hőmérséklet létezésének kimondásán. Végtelenül fontos és alapvető az a tény, hogy létezik az egyensúly felé való törekvés tendenciája. Ami azonban nem azt jelenti, hogy az egyensúly szükségszerűen létre is jön. Ez ma már triviálisnak tűnik, de nagy és félreértésekkel terhelt viták hoz vezetett Nernst törvényével kapcsolatban. Nernst azt mondta, hogy az entrópia abszolút zéró hőmérsékletekhez közeledve nullához tart, később azonban kiderült, hogy ez nem mindig igaz. Vannak ugyanis befagyott nemegyensúlyi állapotok is.

Fowler, a híres elméleti fizikus élesen bírálta Nernstet [4]. Milyen predikció az, ami nem tudja egyértelműen megmondani, hogy valami igaz-e? Akkor az semmire sem jó.

A lényeg az, hogy a folyamatok az egyensúly felé törekednek, nem pedig távolodnak tőle. Előfordulhat, hogy az egyensúly sohasem áll be, a Gibbs által passzívnak nevezett erők; a belső súrlódás miatt. Ez azt jelenti, hogy a termodinamika nem predikció abban az értelemben, ahogy a csillagászat képes predikcióra, ahogy a csillagászat előre tudja jelezni egy bolygópálya alakulását. A termodinamika azt írja le, hogy mi történik az egyensúlyi állapotban. A Gibbs formalizmus az egyensúlyi állapotban érvényes.

Gyakran beszélnek arról, hogy a termodinamika érvényes-e? Ilyenkor nem arra gondolnak, hogy például a hő az alacsonyabb hőmérsékletről a magasabb hőmérséklet felé fog esetleg áramlani, hanem arra, hogy amikor nem állt be az egyensúly, akkor a Gibbs-féle alapegyenletek nem érvényesek egzakt módon, mivel a változók nincsenek definiálva.

Hogyan tudjuk megállapítani, hogy létrejött-e az egyensúly? Úgy, hogy ellenőrizzük a termodinamikai összefüggések teljesülését. A termodinamika megmondja, hogy hogyan viselkedik a normális egyensúlyi állapot. A vizsgált rendszerünket össze kell hasonlítani a normális egyensúlyi állapottal, a kvantitatív termodinamikai összefüggések felhasználásával.

Tegnap Martinás Katalinnal beszélgettem, és ő a következő megfogalmazást ajánlotta: “A termodinamika nem prediktív, nem deskriptív, hanem restriktív tudomány."

Most nézzük meg azt, hogy mi újat lehet mondani az első főtétellel kapcsolatban! Az első főtételt általában az energia megmaradással összefüggésben tanuljuk illetve tanítjuk. A 19. században az energiamegmaradós törvénye ismert volt. A kinetikus energia és a potenciális energia összege állandó, kivéve természetesen azt az esetet, amikor disszipatív csök is fellépnek. Ez utóbbi esetben az energia nem marad meg. Ha azonban a molekuláris erőket is figyelembe vesszük, akkor az energiamegmaradós teljesül. A molekuláris energiát azonban közvetlenül nem tudjuk mérni. Kellemes érzés ugyan, hogy az energiamegmaradás teljesül, de nem sokat tudunk vele kezdeni azon túl, hogy kalorimetrikusan mérjük a termodinamikai rendszer energiatartalmát, és az energiát kifejeztük a nyomás, hőmérséklet, térfogat illetve egyéb makroszkopikus mennyiségek függvényében. Ezt viszont nem tudnánk megtenni, ha nem lenne egyensúly. Nem igaz tehát az az állítás, hogy az egyensúlynak csak a második főtételben van szerepe, a-r. első főtételnél nincs rá szükség. Hiszen nem beszélhetünk energiafüggvényről, ha nem biztosítjuk előbb az egyensúly létezését.

Térjünk most át a második főtételre. A második főtétel segítségével határozzuk meg az entrópiafüggvényt,

(1)

Azt mondhatnám, hogy a második főtételhez semmit sem kell hozzátenni, az úgy jó, ahogy a könyvekben van, csakhogy ez nem a teljes igazság. Az rendben van, ahogy az entrópiát meghatározzák, mivel minden laboratóriumban végzett kalorimetrikus mérés entrópia különbséget, és sohasem abszolút entrópiát ad. A klasszikus termodinamika idejében ezt adottságnak tekinthették. Az Isten úgy határozott, hogy az abszolút entrópiát nem határozhatjuk meg. Ezenkívül a klasszikus statisztikus mechanikában a fáziscella választásának önkényessége szintén egy tetszőleges állandót hoz be az entrópia kifejezésbe, és semmit sem tudunk az entrópia állandóról. És, ami a legfontosabb: nincs is semmi szükség az entrópia konstansra.

A 20. századi kvantummechanikában azonban kiderült, hogy meg lehet határozni az abszolút entrópiát. A kvantumelméletben ki tudjuk számítani az állapotot, és az abszolút entrópiának van jelentése.

Most érkeztünk el a harmadik főtételhez. Annak, hogy az entrópia “klasszikus" megközelítésében egy integrációs konstans határozatlan marad, az akkoriban vizsgált problémák szempontjából nem volt jelentősége. Walther Nernst azonban felismerte, hogy ez a klasszikus elmélet hiányossága. Ezt küszöbölte ki a harmadik főtétellel, ami kimondja, hogy minden termodinamikai egyensúlyban lévő rendszer entrópiája abszolút nulla fokon nullává válik. Ennek a törvénynek fontos következményei vannak, melyek nagy jelentőségre tettek szert, különösen az alacsony hőmérsékletek fizikájában. A tételt azonban általában egyszerűen a kvantummechanika következményének tekintik. Ebben az előadásban arra szeretném felhívni a figyelmet, hogy Nernst ezt a törvényt a kvantummechanikától függetlenül fedezte fel, ami a fenomenologikus módszer legnagyszerűbb eredményeinek egyike. Nernst a tétel levezetésekor nem használta fel a kvantumelméletet, hanem inkább egy olyan új vonását fedezte fel, amely megvilágítja az elmélet körül folyó állandó fogalmi vitákat.

A Gibbs féle termodinamika keretei között jelent meg az első jele annak, hogy az energia- és az entrópiaállandó érdekes lehet. Az U=U(V,S) fundamentális egyenlet egy egykomponensű homogén termodinamikai fázis minden egyensúlyi tulajdonságát tartalmazza, és ebben a teljes (integrált) energia és entrópia szerepel, nem csak a változás. (Az összetett rendszerekre vonatkozó általánosítás könnyen elvégezhető). A fundamentális egyenlet létezésének nincs mechanikai megfelelője, mivel a klasszikus mechanikában az objektumok tulajdonságai a tetszőleges kezdeti feltételekből következnek.

Gibbs nagyon közel jutott ahhoz, hogy a fundamentális egyenletre egy teljes elméletet építsen fel, számos vonást azonban később kellett hozzáfűzni. Noha a fundamentális egyenlet csak egyensúlyi állapotokat tartalmaz, a formalizmus keretei között kezelhetők olyan összetett állapotok is, amelyek belső kényszerek relaxációjával jönnek létre. Az összetett rendszereknek a használatát először Planck tette világossá, amikor megmutatta, hogy enélkül milyen konfúzió veszi körül a Gibbs féle szélsőérték elveket.

Az alacsony hőmérsékletű fizika technikájának felfedezése a század elején a Gibbs féle termodinamika fontos alkalmazási területét jelentette, ugyanakkor az abszolút nulla hőmérséklet ismertté válása a formalizmus kiterjesztéséhez is vezetett. Lehetővé vált az integrációs konstans problémájának pontos megfogalmazása, valamint U és S kifejezése a fajhő integráljaként.

Az alacsony hőmérsékletek fizikája szintén 20. századi tudomány. Az oxigén és a nitrogén cseppfolyósításától eltekintve, minden új. Az, hogy az abszolút zérus hőmérséklet olyan fogalom, amivel dolgozni lehet, ahogy ezt Kürti Miklós is említette, csak ebben a században lett világos.

Ha elfogadjuk, hogy beszélhetünk abszolút zérus hőmérsékletről, akkor az energia és entrópia konstansnak határozott értelmet tulajdoníthatunk. Az energiát felírhatjuk a zérusponti energia és a fajhő integráljának az összegeként.

(2)

Az alacsony hőmérsékleteket kutató fizikus a fajhőből indul ki, azt méri közvetlenül, és minden egyébre abból következtet.

Az entrópia hasonló függvény,

(3)

A szabadenergia kifejezése pedig:

(4)

A konstansokat is kiírva:

(5)

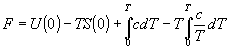
Mit mondhatunk az entrópia konstansról? A fizikusnak nem sok dolga van vele; amikor hőmérséklet kiegyenlítődési vagy diffúziós kísérletet végez, az entrópia konstans mindig kiesik.

A kémiában azonban más a helyzet. Kémiai reakciók esetében az entrópia állandó megjelenik a reakcióhő kifejezésében, ezért a vegyész számára ennek van fizikai jelentése.

Az entrópiaállandó azonban nem határozható meg kísérletileg, és ha az önkényes TS₀ mennyiségnek kísérleti jelentősége volna, akkor nem létezne egy határozott kémiai egyensúly. Az entrópiaállandó a hőmérséklettel megszorozva jelenik meg, ezért határozatlan marad. Abszolút zérus hőmérsékleten természetesen az energia és a szabadenergia megegyezik, véges hőmérsékleteken azonban nem. Az entrópiaállandó egy fizikai illetve kémiai szempontból jelentéssel bíró tag, nem lehet egyszerűen megkerülni.

A termodinamika klasszikus formalizmusa számot ad a hőátadásról és a diffúzióról, és megadja a kémiai egyensúly tömeghatás törvényét is:

(6)

ahol R a gázállandó, a szabadenergia változása, K a tömeghatás állandó. (Ez a koncentrációtól független, de függ a hőmérséklettől, és a nyomástól.) Ha ezt az összefüggést komolyan vesszük, akkor a gyakorlatilag fontos K(T,P)-t meg lehet határozni a szabadenergia változásból, ami viszont a mérésekből számítható.

A vegyészeknek fontos a tömeghatás állandó. Az S₀ határozatlansága miatt azonban nem tudjuk kiszámítani a szabad energiából. Most érkezünk el Nernsthez.

Nernst empirikus alapon biztos volt abban, hogy az egymással reakcióba lépő vegyületek egy olyan egyensúlyi állapot felé tartanak, amelyben a reagensek mólszámai a hőmérséklet és a nyomás által jól meghatározott értéket vesznek fel. A klasszikus formalizmus azonban nem adta meg a kívánt eredményt. Ha ránézünk a 5. egyenletre, akkor látjuk, hogy miért.

Míg az U(0) energiaállandó a reakcióhőkből megállapítható, az S(0) entrópiaállandó tetszőleges, ami ellentmond a szabadenergia meghatározott voltának. Ezenkívül, az utolsó tag logaritmikusan végtelenné válik, ha a fajhő állandó, a klasszikus statisztikus mechanikának megfelelően. (Abban az időben természetesen még nem voltak renormálási eljárások.) A kérdést tehát alaposabban, a lényeget érintőbb módon kellett megoldani. Mindkét nehézség megszűnik, ha posztuláljuk a következőt:

(7)

amint azt Nernst a termodinamika harmadik főtételében kimondta. A fajhő nullává válása ennek a posztulátumnak a következménye.

Nernst a nitrogén fixáció problémájára keresett gyakorlati megoldást. 1898-ban Crookes professzor előadást tartott a British Association keretében, és megkongatta a vészharangot, hogy a világ salétrom készletei kimerülnek. A robbanóanyagokat nem nagyon említette, inkább azt hangsúlyozta, hogy a világ éhezni fog, ha nem találnak ki valami megoldást. A műtrágyaként használt nitrogén a chilei guanó lerakódásokból származik, ez azonban nagyon korlátozott mennyiségű. Mesterségesen kellene előállítani. Végül is, a levegőben van elég nitrogén és hidrogén. A nitrogén és a hidrogén között kellene reakciót létrehozni, hogy ammóniát kapjunk. Ezt hívták ebben az időben nitrogén fixációnak. Az egyetlen baj az volt, hogy ez a reakció nem ment végbe.

Az áttörés két embernek volt köszönhető. Egyikük Walter Nernst, a másik Fritz Haber volt. A nitrogén fixáció problémájával két különböző aspektusból foglalkoztak, s ez a különbség mais nagyon érdekes. Nernst azt kutatta, hogy milyen hőmérsékleti és nyomás viszonyok mellett lehet elegendő mennyiségű ammóniát előállítani. Ebből a célból ki akarta számítani a szabadenergia változást,

(8)

és rájött, hogy nem tudja.

Az energia csak nitrogén, hidrogén és az ammónia tulajdonságaitól függ. Ezek a laboratóriumban mind meghatározhatók. Elvben ki lehet számítani.

A zérus ponti entrópia határozatlansága miatt a szabadenergia második része, a hőmérséklet és az entrópia szorzatát tartalmazó tag nem számítható ki a mért adatokból. Nernst felismerte, hogy ha ez a tag nulla, akkor a számítás elvégezhető. Rájött arra, hogy ha megköveteljük, hogy az entrópia abszolút nulla fokon zérus legyen, akkor mindkét nehézség megoldódik, hiszen az entrópiaállandó eltűnik, és a fajhőnek nullához kell tartania. Nernst ily módon kiszámolta az ammónia egyensúlyt, és megállapította, hogy milyen körülmények között megy végbe a reakció. Ekkor azonban feladta a problémát, mert a reakció nem ment elég gyorsan végbe. Sok egyéb dolog foglalkoztatta, áttért más kérdésekre.

Fritz Haber sokkal inkább alkalmazott vegyész volt, mint Nernst, és kihívást látott a feladatban. Mit testnek a vegyészek, ha egy reakció nem megy végbe? Katalizátort használnak. Keresni kezdett, és talált is egy olyan katalizátort, melynek segítségével elfogadható körülmények között végbemegy a reakció. Ezután kapcsolatba került a vegyészmérnök Bosch-sal, aki kidolgozta az ipari méretű megvalósítást. Létrejött a Haber-Bosch eljárás, amiért két Nobel díjat osztottak ki. Nernst az egyensúlyi probléma megoldásáért kapta a Nobel díjat, Haber a reakció tényleges létrehozásáért. Az eljárást 1913-ban kezdték alkalmazni, egy évvel az első világháború kitörése előtt. Ha ez az eljárás nem létezett volna, akkor Németország egy évnél tovább nem tudta volna folytatni a háborút, mert kifogyott volna a robbanóanyagból. Amint Kurt Mendelssohn nagyon érdekes könyvéből kiderül, az a gyár, ahol a nitrogén-fixáció történt a Berlint Hamburggal összekötő vasút mentén 3 km hosszan terült el. Egy hihetetlen nagy gyár kellett a gyakorlati megvalósításhoz. Nagyon érdekes, hogy a fizikusok akár akarják, akár nem, belebonyolódnak a háborús vonatkozásokba.

Bár sok tankönyv a harmadik főtételt csak mellékesen tárgyalja, látjuk, hogy valójában ennek a szaktudományi fejleménynek messzemenő következményei voltak. Mindezt nagyon érdekesen írja le Kurt Mendelssohn könyvében. Sajnos ez a könyv már az angol és amerikai kiadóknál sem kapható.

Röviddel azután, hogy Nernst publikálta az eredményét, Einstein megerősítette azt az akkor kialakuló kvantumelmélet szemszögéből. A harmadik főtételt általában ebben az összefüggésben tárgyalják.

Noha a fizika és a kémia egyaránt részei a természettudománynak, viszonyuk nagyon bonyolult.

A Nernst által felhasznált elvet a kémiai determinizmus elvének nevezném és úgy érzem, hogy ez a megkülönböztetés valóban fontos. Ez egy lépést jelent a kémiai affinitás ősrégi problémájának a megoldása felé: numerikus válasz nyerhető az egymástól elszigetelt reagensek mérhető tulajdonságaiból. A kémiai determinizmus elnevezés a kanonikus pontmechanika keretei között használt mechanikai determinizmus fogalmára emlékeztet.

A fizikusok joggal voltak büszkék arra, hogy Newton felfedezte a csillagászatban a mechanikai determinizmust, azaz hogy egy bolygópályát előre lehet jelezni. Egy reakciót előrefelézni azonban hasonlóképpen csodálatra méltó.

Makroszkopikus keretek között az ezen elvek köré épülő elméletek teljesen különbözőek. A mechanika állandó objektumok pályamenti elmozdulásával foglalkozik, míg a kémia a belső szerkezet átalakulását tárgyalja. Éppen azért, mivel ezek a problémák különbözőek, az elméletek fogalmi különbségei a makrofizikában nem okoznak konfliktust.

Teljesen más azonban a helyzet, ha a klasszikus statisztikus mechanika útján kiterjesztjük a kanonikus mechanikát a mikrofizikára. Az alacsony hőmérsékleten végzett mérésekkel ellentétben ez az elmélet állandó fajhőt szolgáltat. Ez volt az ekvipartíció paradoxon. Ezenkívül, az entrópia alacsony hőmérsékleteken mínusz végtelenhez tart. Mindkét eredmény ellentmond a kémiai determinizmusnak.

A kvantummechanika mindkét nehézséget megoldja, mindazonáltal ezt az elméletet igazságtalanul kritizálják azzal, hogy gyengíti a determinizmus érvényességi körét. Valójában a kvantummechanika összhangban van a kémiai determinizmussal, míg a klasszikus mechanika nincs. A Heisenberg reláció azt mondja, hogy a mechanikai determinizmus korlátozott. A mechanikai determinizmus gyengítéséért bőséges kárpótlást nyújt az, hogy a kvantummechanika alátámasztja a kémiai determinizmus elvét.

A kémiai determinizmus figyelmen kívül hagyása annál is inkább nem megengedhető, mivel a kémiai egyensúly, mint a hőmérséklet és a nyomás függvénye központi jelentőségű a kozmológiában, amikor az ősrobbanás utáni néhány percet vizsgálják.

Végül, a kémiai determinizmus képezi a biológiai szervezetek működésének alapját.

Mindez a következőkben foglalható össze: A múlt században a fizika, kémia és a biológia teljesen inkonzisztens volt, mivel a kanonikus mechanika determinizmusa szellemében nem lehetett őket egyesíteni. Századunk nagy eredménye ezen tudományok messzemenő összhangba hozása a kvantummechanika megjelenésével, és. az összekötő láncszemet a kémiai determinizmus elve jelenti.

1. Kurt Mendelssohn, The World of Walther Nemst, The Rise and Fall of German Science 1864-1941, London 1973.
2. Walter Nernst, “Über die Berechnung chemischer Gleichgewichte aus thermischen Messungen", Nachr. von den königlichen Gesellschaft der Wissenschaften zu Göttingen, 1-40. 1906.
3. R.H. Fowler, E.A. Guggenheim, Statistical Thermodynamics, London, Cambridge Univ. Press 1939.
4. R.H. Fowler, T.E. Sterne, Statistical Mechanics with Particular Reference to the Vapor Pressures and Entropies of Crystals, Rev. Mod. Phys., 4, 635-722, 1932.
5. Tisza László, The Harmony of Educational and Logical Priorities in Thermodynamics, Taormina Conference on Thermodynamics, 1991. febr.

______________________________