A SZELLEM DIADALA Az ANYAG FÖLÖTT - A KÍSÉRLETI FIZIKA DICSÉRETE

Telegdi Bálint
Pasadena,
az Eötvös Társulat tiszteleti tagja

Tapasztalatom szerint bármely egyetem legtehetségesebb fizikus hallgatói inkább elméleti kutatók szeretnének lenni, s ez jellemző az Atlanti óceán mindkét partján. Ritka, ha valaki, aki olyan szellemi kapacitással rendelkezik, mint rmondjuk Gell-Mann vagy Cabibbo, úgy dönt, hogy kísérleti fizikusként csinál karriert. Ez komoly veszteséget jelent a fizika számára, annál is inkább, mert a fizika elsősorban természettudomány. Gyakran kérdeztem magamtól ennek a sajnálatos helyzetnek az okait. Ha ezeket megtaláljuk, talán lehet javítani a helyzeten.

Két tényezőt említenék meg. Az első az a mód, ahogyan a fizikát tanítják lényegében mindenütt. Kétfajta modell létezik, A és B, de egyikük sem továbbítja a hallgatóknak a fontos kísérletek intellektuális tartalmát. Az A modell szerint a hallgató azt hallja, hogy valamely kiemelkedő elme (név szerint), előre megsejtette két jelenség y(x) jellegzetes összefüggését. Ezt az összefüggést aztán később ékesen igazolják kísérletileg (névtelen valakik). Ar B modellben valaki megfigyelte az y(x) rejtélyes összefüggést, amely a maga idejében megmagyarázhatatlannak bizonyult. Később ismét jött egy nagy elme (név szerint), és létrehozott egy elméletet, amely tökéletesen illeszkedett a megfigyelésekhez. A kísérletezők szellemi teljesítményét egyik modell sem továbbítja a hallgatóknak. Ezt két példán szeretném bemutatni: (1) Okun remek könyvében, a "Leptonok és kvarkok"-ban a kísérleteket ritkán írja le - habár a szerzőik ismertek -, az eredményeikre csupán úgy hirvatkoznak, mint "valaki azt találta ...". (2) Egyszer tartottam egy kollégiumot "Híres kísérletek a modern fizikában" címmel a MIT-n. Az előadást fiatal egyetemisták látogatták és ... idős elméleti kutatók. Az utóbbiak közül sokan először hallották, hogy Willis Lamb tulajdonképpen hogyan mérte meg a róla elnevezett "shift"-et, milyen briliáns éleslátásra volt szüksége, hogy elérje célját.

Egész kevesen vonják le azt a helyes következtetést, hogy ugyanannyi szellemi tartalom volt a Lamb kísérletben, mint annak kvantumelektrodinamikai értelmezésében. (Ezen példa értékéből erősen levon az a tény, hogy Lamb valójában egészen kiváló elméleti kutató volt.)

A másik, ettől eltérő ok abból származik, amit én "apakép elmélet"-nek nevezek: A gyakorlatban az összes fizika kurzus elméleti, akár elárulja ezt a kurzus címe, akár nem. Az elméletet oktató elméleti kutatók többnyire jól ismerik azt, amiről beszélnek, a kísérletiek gyakran nem. Így a hallgató (aki talán maga sem érti a tárgyat, mégis csalhatatlanul megérzi az relőadó bizonytalanságát!) azt mondja magában: "Nem akarok olyan lenni, mint ... (és itt a kísérleti kutató neve szerepel), hanem olyan, mint ő (az elméleti kutató neve beillesztve)."

Mit tehetnénk, hogy orvosoljuk ezt a helyzetet? Két dolgot: Először, halasszuk olyan későre a jövő kísérleti és elméleti kutatói képzésének szétválasztását, amennyire csak lehetséges. A különbség a technikában van, nem az elméleti szakértelemben. Másodszor, olyan előadásokat kell tartani, amelyeken részletekbe menően elemezzük ra nagy jelentőségű, briliánsan végrehajtott kísérleteket.

Szeretnék az alábbiakban leírni néhány kísérletet, amelyek ebbe a kategóriába tartoznak, természetesen jóval rövidebben, mint azt egy tanrendi előadáson tenném. Elkerülöm azokat a kísérleteket, amelyek általánosan ismertek (vagy legalábbis azoknak kellene lenniük), remélve, hogy a bemutatott kísérletekkel kellemes meglepetésekkel szolgálhatok. Négy kísérletet tárgyalok időrendi sorrendben.

1911-ben egy fiatal magyar fizikus, Selényi Pál végrehajtott egy kísérletet, hogy kimutassa, létezik a fénysugarak széles látószögű interferenciája [1]. Úgy tűnik, abban az időben komoly vita tárgyát képezte ilyen interferencia létezése. Én nem értem, miért, hiszen az interferencia relativisztikusan invariáns fogalom, és ami széles látószögű az egyik rendszerben, az keskeny látószögű a másikban.

Selényi egyszerű elrendezését vázlatosan az 1. ábra mutatja. A PR üvegprizma és a vékony M csillámlemez között egy fluoreszcens zselatinfilm van, amelynek vastagsága kicsi a látható fény hullámhosszához képest. A koncentrált fénysugár a film egy kis pontját fluoreszcenciára készteti. Az I és II sugár interferenciája következtében interferenciacsík figyelhető meg egy kézi spektroszrkóppal (az ábrán nem jeleztük). (A spektroszkópra azért van szükség, mert a fluoreszcens fény nem monokromatikus.) Selényi azért választotta ezt az elrendezést, mert tisztában volt vele, hogy a széles látószögű interferenciát létrehozó fényforrásnak lényegrében kétdimenziós fényforrásnak kell lennie, amely pontosan párhuzamos a tükörrel. Ez egy körülbelül /7 vastagságú zselatin réteget kíván.

Miután a kísérletet 1938-ban lényegesen kedvezőbb feltételek mellett megismételte [2,3], Selényi a következő eredményeket kapta: (a) a = 45°-nál észlelt minimum sohasem tökéletesen sötét; (b) egy polarizációs szűrőt rbeillesztve, amely úgy volt orientálva, hogy csak azokat az elektromos térerősség-vektorokat engedte át, amelyek merőlegesek voltak a beesés síkjára (1. ábra), lényegesen erőteljesebb interferenciacsíkokat kapott, és a minimum tökéletesen sötét lett. Az analizátort 90°-kal elforgatva az interferenciacsíkok teljesen eltűntek.

Ezek a megfigyelések azt bizonyítják (vagy legalábbis egyezésben vannak azzal a ténnyel), hogy a fluoreszcens fényt elektromos dipólusok emittálják. Ezt bizonyítandó, helyettesítsük a véletlenszerűen irányított dipólust három kölcsönösen merőleges dipólussal. Ezek közül az első (az ábrán nincs feltüntetve) az 1. ábra síkjára merőlegesen rezeg. Ez egyenlő amplitúdójú fényt emittál mind az I mind a II nyaláb mentén, ennélfogva tökéletes minimummalr hoz létre interferenciacsíkokat. A másik két dipólus, (az 1. ábrán 1 és 2) egyáltalán nem hoz létre interferenciát, mivel az 1 nem emittál az I sugár mentén, a 2 pedig a II mentén.

1. ábra A Selényi-kísérlet vázlata. M csillámlemez; PR rüvegprizma. A kettőr között vékony zselatin-fluoreszcens réteg.

Az előbbi egyszerű bizonyítást maga Selényi adta, aki ezzel megfricskázott [4] néhány elméleti kutatót [5], akik bonyolult matematikai formulákkal akarták magyarázni azt a kísérletet, "amelyet legföljebb fél nap alatt végre lehet hajtani, és érthetően megmagyarázható néhány sorban mindenféle matematikai formula nélkül".

Amikor hallgató voltam az ETH-n, körülbelül 40 évvel ezelőtt, elméleti tudásunk nagy részer G. Joos egykötetes "Theoretische Physik" -éből származott. Ebben a könyvben egy bizonyos, forgó platformon végrehajtott interferencia-kísérletet (Sagnac-kísérlet) mint a "Coriolis-erő optikai analógiáját" tárgyalták. Ez az állítás jó néhány éven keresztülr nyugtalanított (mint a Mach-elv egy lehetséges ellentmondása), és emiatt sok könyvet elolvastam ebben a tárgykörben. Így bukkantam rá Michelson csodálatos optikai "Foucault-ingájára".

1904-ben Michelson egy gondolatkísérletben egy kis (gömbi) négyszöget figyelt meg a Föld felszínén, amelyet két főkör és két földrajzi szélesség határol. Egyetlen forrásból kijövő két fénysugarat a kerületen ellentétes irányban végigfuttatva interferenciába hozott. Michelson freltételezte, kétségkívül az akkori klasszikus mozdulatlan éter elmélete alapján, hogy az interferenciacsíkok eltolódása

(1)

ahol A a fénykör által bezárt terület, a szögfrekvencia.

Könnyen látszik, hogy ez általánosan a következőképpen írható:

(2)

azaz a képlet v/c-rendű effektus, tehát lényegtelen, hogy relativisztikusan szemléljük vagy sem.

2. ábra Felülnézet, a Michelson-féle Foucault-kísérlet tükörelrendezését mutatja, AD = FE = 67 m, AF = DE = 37 m.

Sagnac 1913-ban végrehajtotta a kísérletet egy forgó interferométerrel, és megerősítette az előző formulát [7]. Nyilván a mozdulatlan platformon végrerhajtott interferenciára vonatkozó eltolódást is meg tudta határozni ( = 0).

Michelson, aki 1925-ben [8] Gale-lel és Pearsonnal együttműködve végrehajtotta arz általa 1904-ben javasolt kísérletet, a Föld forgását nyilván nem állíthatta meg. Vajon hogyan tett eleget ennek az "ördögi" feladatnak?

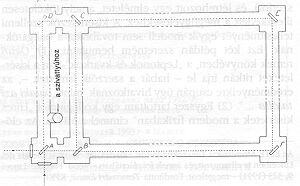
Először is Chicago közelében vákuumcsövekből egy valóban gigantikus interferométert épített (2. ábra). Az interferométer egy hosszú körből (ADEF) és egy rövid körből (ADCB) állt. Mivel a forgásból származó 0 eltolódás arányos a kis kör által bezárt területtel, a fénykör interferenciamintája szolgált referenciaként ( = 0 esetet szimulálva).

Felmerül a kérdés, hogyan lehetne kiküszöbölni a tükrök rossz beállításából származó relatív eltolódást. Az okoskodás a következő: mindkét kör a forrásnak két képét hozza létre: egy valódi és egy visszavert képet (függetlenül az interferenciától vagy a forgástól). E két kép között középen helyezkedik el az interferenciaminta, közepén a nulladrendű interferenciacsíkkal. Mind a rövid, mind a hosszú körből származó központi interferenciacsíkok a valódi és a visszavert kép között félúton helryezkednének el, ha Föld forgása miatt nem lenne közöttük eltérés.

A kétféle képnek ideálisan fedésben kellene lennie. A gyakorlatban a szuperpozíció hiányának a javítására a megfigyelő teleszkópot a forrás képére fókuszálták, és a középső interferenciacsíkok látszólagos relatív elmozdulását egy olyan mennyiséggel korrigálták, amely egyenlő a két kör által létrehozott két kép átlagos pozíciójának különbségével.

Az eredmény tizenhárom megfigyeléssorozat átlagértéke, = 0,230ą0,005. Vessük ezt össze a jövendölt értékkel ( = 570 nm, = 41° 46') = 0,236(2).

A Michelson-Sagnac-effektus ma már nem pusztán tudományos kuriózum, de egy gyakorlati eszköz alapja, a lézer-giroszkópé, amelyet széles körben alkalmaznak tehetetlenségi vezérlésekre. A trükk a -skálából a v-skálára való átváltásban van, az érzékenység ezzel nagymértékben megnő. Egy forgó gyűrű-lézerben a két ellentétesen terjedő fénysugár adott sajátmódusai (L = n )v = v / frekvenciával különböznek. Ezeket interferáltatva lebegést kapunk 2 v v / c=4 (R/ ₎v_F frekvencián, ahol R a (köralakú) gyűrű-lézer sugara, v_F a Föld forgási frekvenciája 10^-5 s^-1. Ezért például R ~ 1 cm esetén ~ 1 Hz, ami jól detektálható hangfrekvencia. Ez a berendezés ma már a kereskedelemben kapható.

3. ábra Impulzusmomentum megmaradás a GGS helicitás-kísérletben.

Amikor 1957 januárjában felfedezték a tükrözési szimmetria hiányát (a paritás megmaradás sérülését) a -bomlásban, lényegében az összes megbízható kísérlet elektronokon (pozitronokon) alapult. Elfogadott volt, hogy de égetően nyitott kérdés volt, hogy vajon v = v_B (és ) vagy v = v_J (és = v_B). Itt a B (bal) és J(jobb) index a részecske bal-, illetve jobbkezességét jelöli, azaz a helicitást, amelynek a definíciója: . Az (e_B, v_B ) választás a gyakorlati szóhasználatban a "V, A csatolásnak" felel meg, míg az (e_B, v_J )választás az "S, T csatolásnak". A kérdést körülbelül egyidőben válaszolták meg polarizált neutronok bomlásakor fellépő korrelációk vizsgálatával [8], illetve az emittált neutrínók helicitásának közvetlen mérésével.

A neutrínók helicitását lehetetlen olyan módszerekkel meghatározni, amelyeket az elektron helicitásának méréséhez használnak, mint például polarizált elektronokon végzett szóráskísérlet, mivel a neutrínók kölcsönhatása igen gyenge. Ezért valami gyökeresen új ötletre volt szükség.

Maurice Goldhabet követve tekintsünk egy olyan bomlási sort, amely az A anyamagból indul (J_A = 0), és B* gerjesztett állapoton keresztül (J_B* = 1) eljut a B leánymagba (J_B = 0). Így a következő bomlási sémát kapjuk:

A + e^- (e-befogás) B* (legerjesztődés) B (alapállapot) + . Ábrázoljuk grafikusan az impulzus és az impulzusmomentum megmaradását, feltéve hogy v = v_B (3. ábra).

A gerjesztett B* mag repülésének irányába kibocsátott foton balkezes lesz ( = _B ), azaz a helicitása ugyanolyan, mint az emittált neutrínóé. Nyilvánvalóan ez a helicitás-átvitel akkor is bekövetkezne, ha v = v_J volna. (Megjegyezzük, hogy a rajz mindkét lépésben egyenlő energiakibocsátást tételez fel.) Így kísérletileg (a) meg kell határozni a kibocsátott r-sugárzás cirkuláris polarizációját, (b) ki kell mutatni, hogy az valóban irányába lépett ki. Az (a) lépés viszonylag könnyű, mágnesezett vas szolgálhat analizátorként. A (b) lépés szövevényesebb - a megvalósításához rezonanciafluoreszcenciát kelrl alkalmazni.

Tételezzük fel, hogy a laboratóriumi koordinátarendszerben a B* mag (E₀ gerjesztési energiával) nyugalomban van, és az általa kibocsátott fotont akarjuk szóratni. A visszalökődés miatt a foton E = c p energiája kevesebb lesz, mint E₀, csak körülbelül E = E₀ - / 2 Mc² . Az abszorpció során a mag ismét visszalökődést szenved, így a gerjesztésre felhasználható energia E = E₀ - / 2 Mc². Tehát a rezonanciafeltételhez / Mc² energia hiányzik. Amikor B* mag a repülése irányában bomlik, ahogy a 3. ábra mutatja, a rezonancia-feltétel helyreáll (feltéve, hogy p_v ~ p ).

Egy kis gondolkodással kimutatható, hogy a feltételek egy kivételes rendszerének kellett egyszerre összeállnia, hogy ez a kísérlet a gyakorlatban megvalósítható legyen, pontosabban

4. ábra A GGS helicitás-kísérletben felhasznált berendezések

(a) a spin sor 0-1-0;

(b) a spin-paritás sor 0^--1^--0⁺. A B* mag repülés közben olyan gyorsan bomlik, hogy -sugárzásának E1-nek kell lennie (B alapállapota elkerülhetetlenül 0⁺ spin-paritású). Így B*-nak 1^--nak kell lennie. Hogy az e-befogás megengedett legyen, A spin-paritása 0^-.

(c) A c p_v és E₀ energiáknak meg kell egyezniök.

(d) Ezeknek az energiáknak kellően nagynak kell lenniük (néhány 100 keV), hogy elkerüljük a Mössbauer-effektust, és hogy a polarizációanalízis lehetséges legyen.

(e) A stabil B magnak gyakori előfordulású izotópnak kell lennie, hogy a gyakorlatban szórómagként használhassák.

Mindezek a feltételek teljesülnek A = ^152mEu, B = ¹⁵²Sm esetében. Megjegyezzük, hogy ezt a bomlási sort abban az időben csak Goldhaber és társai ismerték.

Napóleon egyszer azt mondta, "Isten mindig az erősebb hadsereg oldalán áll", én pedig azt mondom, Isten mindig a találékony kísérletezők mellett van.

A 4. ábra Goldhaber és munkatársai kísérleti elrendezését mutatja. Eredményük a következő volt, h_v = -1 ą 0,3, azaz az e-neutrínó balkezes.

A müon-befogás teljesen analóg módon történik, mint az e-befogás, ahogy ezt elsőként Bruno Pontecorvo felismerte. Így rögtön kísért a gondolat, hogy helicitásának meghatározása az imént vázolt GGS kísérlet mintájára történjen. Az analógia azonban megtörik, mivel a -befogáskor felszabaduló energia (p_v) jóval nagyobb, mint bármelyik E₀ nukleáris gerjesztési energia. Tehát B* helicitásának meghatározására egy teljesen különböző utat kell találni, mégha azonos spin-sort tételezünk is fel. Tekintsük a következő bomlási sort: A(0⁺) +  ^-   B(1⁺) +  _; B(1⁺)   C(0⁺) + e^- +  ; C = A.

5. ábra Grenács és társai helicitás-kísérletében használt berendezések
(a) A kísérlet alapja: C szénréteg, D rdepolarizátor, P polarizációt megőrző réteg; T₁, T₂ teleszkópok.
(b) A valódi elrendezés: S szórócentrumok, Ab abszorbens, HC Helmholtz-tekercs, S₁, S₂ sugárzásdetektor, 1, 2, 3 sokcsatornás proporcionális kamrák, B a longitudinális polarizációt fenntartó tér. S r1000 db szendvicsből áll: A1(1,5 m) / C (60 g/cm² / Ag (1200 g/cm²).

A B mag longitudinális polarizációja közvetlenül mérhető az A magra való bomlásakor fellépő ismert (maximális) le-fel aszimmetrián keresztül; az egyetlen - nagyon nem triviális - feltétel, hogy B eléggé rövid életű legyen, hogy elbomlása előtt ne depolarizálódjon az anyagban.

6. ábra (a) A polarizációk vázlatos összefüggése a kétféle halmazorientációban (a Pr polarizációt megőrző réteg határa rbeárnyékolt). (b)r A szórómagok halmazának kétféle orientációjában mért polarizáció eredményei. Az adatok a két teleszkóp átlagát mutatják: a függőleges vonalkák a független működést jellemzik. , i az irányírtottság jellemzője, azaz Er(előre) vagy H(hátra); N a -arány Br mezővel és nélküle.

A Természet ismét kegyes és egy megfelelő spin-paritású bomlási sort szolgáltat: