Fizikai Szemle 1997/5. 157.o.
PÁROLT MACSKA
Geszti Tamás
ELTE Atomfizikai
Tanszéke
A szóbanforgó
macska természetesen Schrödinger boldogtalan
kedvence, aki elpusztul, ha egy radioaktív magból
kiszabaduló 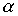 -részecskét detektál egy
számlálócső, amelyhez csatlakozó
szerkezet összetör egy méreggel teli fiolát
[1]. Amíg az
-részecskét detektál egy
számlálócső, amelyhez csatlakozó
szerkezet összetör egy méreggel teli fiolát
[1]. Amíg az 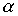 -részecske a magba bezárva marad,
a macska él. Mivel az
-részecske a magba bezárva marad,
a macska él. Mivel az 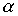 -bomlás alagúthatással
történik, ami a legtipikusabb kvantummechanikai jelenségek
egyike, világos, hogy az
-bomlás alagúthatással
történik, ami a legtipikusabb kvantummechanikai jelenségek
egyike, világos, hogy az 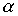 -részecske tulajdonképpen
a magba zárt és a magból kiszabadult állapot
szuperpozíciójában van. Ha elfogadjuk, hogy
a kvantumelmélet a világ minden dolgainak elmélete,
akkor a szuperpozíció nem csak az
-részecske tulajdonképpen
a magba zárt és a magból kiszabadult állapot
szuperpozíciójában van. Ha elfogadjuk, hogy
a kvantumelmélet a világ minden dolgainak elmélete,
akkor a szuperpozíció nem csak az 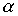 -részecskére,
hanem a macska és az
-részecskére,
hanem a macska és az 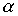 -részecske együttesére
is vonatkozik, legalábbis addig, amíg rá
nem nézünk a macskára és élőnek
vagy döglöttnek nem találjuk.
-részecske együttesére
is vonatkozik, legalábbis addig, amíg rá
nem nézünk a macskára és élőnek
vagy döglöttnek nem találjuk.
Schrödinger macskája
tehát élet és halál kvantummechanikai
szuperpozíciójában lebeg, mivel sorsa összefonódott
egy potenciálisan macskagyilkos 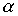 -részecskéével
[1]. Schrödinger macskáját párolt macskává
pedig nem a konyhaművészet teszi, hanem a kísérletező
fizikusok művészete, amely őt lepárlással
kiszabadítja ebből az összefonódásból,
s ezáltal érzékelhetővé teszi
élet és halál szuperpozíciójának
hasonlíthatatlanul bódító illatát.
-részecskéével
[1]. Schrödinger macskáját párolt macskává
pedig nem a konyhaművészet teszi, hanem a kísérletező
fizikusok művészete, amely őt lepárlással
kiszabadítja ebből az összefonódásból,
s ezáltal érzékelhetővé teszi
élet és halál szuperpozíciójának
hasonlíthatatlanul bódító illatát.
Az említett összefonódás
a kvantummechanikának talán legrejtélyesebb
tulajdonsága: ha két részrendszer egyszer
kölcsönhatásba került, akkor egyéni
sorsuk megszűnik, akár egy házasságban
[2]; még valószínűségi kijelentést
is csak együttesükre tudunk tenni. Az adott esetben:
ha a macskának és az 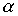 -részecskének
semmi köze nem lenne egymáshoz, kettejük sorsának
(élő vagy döglött macska, kisugárzott
vagy ki nem sugárzott
-részecskének
semmi köze nem lenne egymáshoz, kettejük sorsának
(élő vagy döglött macska, kisugárzott
vagy ki nem sugárzott 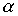 -részecske) négyféle
kombinációja valósulhatna meg. Mivel azonban
sorsukat a méreg összefonta, csak két lehetőség
marad: 1) az a
-részecske) négyféle
kombinációja valósulhatna meg. Mivel azonban
sorsukat a méreg összefonta, csak két lehetőség
marad: 1) az a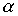 -részecske még a radioaktív
magban van és a macska él, 2) az a
-részecske még a radioaktív
magban van és a macska él, 2) az a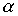 -részecske
kialagutazott a magból és a macska elhalálozott.
Ez a fajta összefonódás a gyökere a híres
Einstein-Podolsky-Rosen-paradoxonnak is [3].
-részecske
kialagutazott a magból és a macska elhalálozott.
Ez a fajta összefonódás a gyökere a híres
Einstein-Podolsky-Rosen-paradoxonnak is [3].
Hogy egy árnyalattal
konkrétabbá tegyük a fejtegetést és
az állatvédőket is megnyugtassuk: az alábbiakban
olyan kísérletekről lesz szó, amelyekben
Schrödinger elhíresült macskáját
élettelen (bár, mint tudjuk, életrevaló)
atomokkal vagy fotonokkal modellezik, amelyek sajnálatos
kényszerűségből elszürkített
képe élet és halál költészetének!
- két, makroszkopikusan megkülönböztethető
állapot szuperpozíciójába kerülnek.
Ilyen szuperpozíciók
létrehozása igazi macskával nyilvánvaló
képtelenség, csak éppen nem igazán
tudjuk, hogy miért. Atomokkal és fotonokkal éppen
ellenkezőleg: úgy érezzük, hogy a dolog
nem is jelentene még csak egy közönséges
világraszóló szenzációt sem,
mivel például a Stern-Gerlach-kísérletben
egy atom több centiméternyire eltávolodott
pályák szuperpozícióján mozog.
A játszma éppen azért folyik, hogy a végén
megértsük, miféle fizikai szükségszerűség
jelöli ki a határt a mikroszkopikus világ,
ahol szuperpozíciók léteznek, és a
makroszkopikus világ között, ahol helyettük
csak a különböző lehetőségek
inkoherens "keverékei" lépnek föl:
egyszerre csak az alternatívák egyike valósul
meg, véletlenszerű választással, amelyről
a kvantummechanika "csak" a valószínűségeket
árulja el.
Az átmenetet a makroszkopikus
és mikroszkopikus határán levő mezoszkopikus
rendszerekben remélhetjük megfigyelni, mint amilyen
egy néhány milliméteres ioncsapdában
rezgő ion, vagy egy 8-10 fotonnyi amplitúdójú
koherens állapotba gerjesztett üregrezonátor,
amely a kváziklasszikus mechanikai rezgés elektrodinamikai
megfelelője. Az érdekes szuperpozíció
az lenne, ha az oszcillátor - akár mechanikai, akár
elektrodinamikai egyszerre tartózkodna pályája
két különböző helyén.
A két hely természetesen
nem élesen valósul meg (gondoljunk a Heisenberg-féle
határozatlansági relációra): igazából
két jól elkülönülő hullámcsomag
kialakulására számítunk. Ezek véges
kiterjedésük miatt enyhén átfednek egymással,
ami interferenciához vezethet.
Schrödinger macskájának
gyanús furcsasága okot ad, hogy kételkedjünk
a szuperpozíció tartós fennmaradásában:
valami olyat várunk, hogy a környezettel való
kölcsönhatás elmossa a két hullámcsomag
interferenciaképességét (ezt hívják
dekoherenciának), mégpedig annál gyorsabban,
minél távolabb kerül egymástól
a szuperpozíció két ága [4]. Mivel
a változás természetéről nincs
igazán világos képünk, önként
kínálkozik az a stratégia, hogy egyetlen
biztos pontként éppen az interferencia lehetőségének
időbeli változását próbáljuk
kísérletekkel követni.
Itt azonban egy akadályba
ütközünk. Hogy megértsük, mi a baj,
térjünk vissza a jólismert Stern-Gerlach-kísérletre.
Az inhomogén mágneses mezővel szétválasztott
két pálya (mondjuk, E(egyik) és M(másik))
összefonódik az atom spinjével; a legegyszerűbb
esetben feles spint tekintve, például a függőleges
mágneses mezőben felfelé illetve lefelé
mutató spin-állapottal:
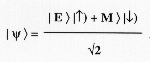
Ez az összefonódás,
bár nélküle nem lehetne Stern-Gerlach módszerével
spint mérni, szinte lehetetlenné teszi, hogy a szuperpozíció
fennmaradását a két tag interferenciájából
észlelhessük, hiszen a spinállapotok nem interferálnak
az át nem fedő pályák miatt, a pályák
pedig az ortogonális spinállapotok miatt. Olyan
fizikai mennyiségben kellene interferencia-járulékokat
kimérni, amely hely- és spin-változókra
egyaránt érzékeny. Ez, ha nem is mindig lehetetlen,
a megoldás útja másfelé vezet: itt
segít a macskának a bevezetőben említett
lepárlása.
Az újszerű gondolat
az, hogy először forgassuk el a spineket z-ből
x irányba, ami a fenti állapotvektort a következőbe
viszi át:
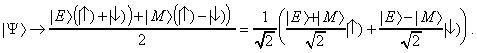
Az utóbbi írásmódból
talán már látszik a lepárlási
művelet vége. Megmérjük a spint és
például felfelé állónak találjuk,
ezzel a pálya hullámfüggvényét
átvittük a két makroszkopikusan különböző
pályából szuperponált 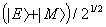 állapotba, amely ezáltal megszabadult a különböző
spinállapotokkal való összefonódás
terhétől. Hasonlóan, lefelé álló
spin megfigyeléséhez az
állapotba, amely ezáltal megszabadult a különböző
spinállapotokkal való összefonódás
terhétől. Hasonlóan, lefelé álló
spin megfigyeléséhez az
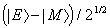 állapot tartozik.
Az ilyen, tisztára párolt makroszkopikus szuperpozíciót
szokás manapság (Yurke és Stoler
nyomán) Schrödinger-macskának nevezni (talán
nem meglepő: az első kombináció neve
"páros macska", a másodiké természetesen
"páratlan macska"). A két spinállapot
mérési gyakorisága az amplitúdók
abszolútérték-négyzetéből
adódik, felhasználva, hogy az |E> és |M> állapotok
egyre vannak normálva:
állapot tartozik.
Az ilyen, tisztára párolt makroszkopikus szuperpozíciót
szokás manapság (Yurke és Stoler
nyomán) Schrödinger-macskának nevezni (talán
nem meglepő: az első kombináció neve
"páros macska", a másodiké természetesen
"páratlan macska"). A két spinállapot
mérési gyakorisága az amplitúdók
abszolútérték-négyzetéből
adódik, felhasználva, hogy az |E> és |M> állapotok
egyre vannak normálva:
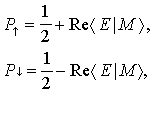
ahol <E | M> az "egyik"
és "másik" pálya-hullámfüggvény
skalárszorzatát jelenti. A skalárszorzat
akkor nem nulla, ha a két pálya nem klasszikusan
éles, hanem a kvantummechanikai kiszélesedés
miatt enyhén átfed. Ez az a tag, amelyben megjelenik
a keresett interferencia: ennek kiméréséből
olvasható le, bírták-e annyira az |E> és
|M> állapotok a megmacskásodást, hogy utána
még képesek maradtak az interferenciára.
A fenti játékos
programot persze könnyebb elmesélni, mint megvalósítani.
Már az is képtelenségnek látszik,
hogy miután a pályákat szétválasztottuk,
mégis egyszerre mérhessük meg a teljes szuperpozícióra
a spin értékét. A kibúvót a
már említett mezoszkopikus rendszerek jelentik,
amelyekben az "egyik" és "másik"
pályát egy oszcillátorban létrehozott
kettős hullámcsomag csúcsai jelentik. Ezenkívül
még egy helyen ki kell használni a kvantummechanika
hallatlan hajlékonyságát: nevezetesen azt,
hogy tucatnyi módon lehet feles spinhez hasonlóan
viselkedő kétállapotú "kvázi-spin"
szabadságfokokat létrehozni, majd a spinforgatásnak
megfelelő műveletet végrehajtani rajtuk, végül
elvégezni magát a kvázi-spin mérését,
amelynek statisztikájában, mint nemes vad lábanyoma,
megjelenik a várt interferencia a kváziklasszikus
szuperpozíció két ága között.
Évekig tartó próbálkozások
után, amelyek során a lehetőségek
végiggondolásában magyar fizikusok is jeleskedtek,
tavaly ért célba két kutatócsoport:
David Wineland csapata a boulderi National Institute for
Science and Technologyban és Serge Haroche laboratóriuma
a párizsi École Normale Supérieure-ben.
Hogy megértsük, mit tett a két csoport a sikerért,
röviden tekintsük át, mi volt a Schrödinger-macska
állapotába átvitt, klasszikus mozgásra
képes szabadságfok, illetve mi volt a spinszerű,
kétállapotú, forgatható, majd megmérhető
szabadságfok a két megvalósult kísérletben.
- Boulderban a "klasszikus"
szabadságfok egy ioncsapdában rezgő berillium-atom
koordinátája. Ennek az atomnak két, különböző
hiperfinom kvantumszámhoz tartozó alapállapota
van, amelyek energiája alig különbözik:
ezek alkotják a "spint". A spinforgatás
stimulált Raman-átmenetekkel történik,
a spinmérés a mélyebb alapállapot
kisöprésekor keltett fluoreszencia detektálásával
történik. Kellett hozzá többek között
a világ legjobb ioncsapdája és hangolható
lézerei, valamint élénk fantázia a
célhoz vezető spinforgató impulzussorozat
kitalálásához.
- Párizsban a
"klasszikus" szabadságfok egy mikrohullámú
üregrezonátorban keltett fotonmező koherens
állapota, a "spint" pedig egy az üregen
átrepülő rubídium-atom két magasan
gerjesztett állapota jelenti. Spinforgatást rádiófrekvenciás
tekercseken való átrepüléssel lehet
megvalósítani; a detektálás a két
atomi állapotot megkülönböztet6 ionizációs
detektorral történik. A méréshez - egyebek
között - szükség van egy 5 · 107
jósági tényezójű üregrezonátorra,
valamint olyan mézertechnikára, amely az n = 50 és 51
főkvantumszámú, egyéb kvantumszámaiban
is teljesen meghatározott atomi állapotok kiválasztásán
kívül még - Doppler-effektus felhasználásával
- az atomok sebességét is hatékonyan kézben
tartja. A fotonokon táplált Schrödinger-macska
interferenciájának megfigyeléséhez
két egymásután érkező atom
ionizációs jele közötti korrelációkat
kell kiértékelni. A méréssorozat megtervezése
persze itt is egy kiváló csapat pezsgő fantáziájából
született meg.
A dekoherenciát, amely
a boulderi optikai kísérletben csak mint az interferenciajel
kontrasztjának csökkenése jelenik meg, a párizsi
mikrohullámú mérés már követni
tudja a kvantumosból a klasszikusba vezető úton,
figyelve a foton-macska két állapotának:
életnek és halálnak eltávolodását.
A kvantum-klasszikus határról, amelynek ködbevesző
hegycsúcsait eddig csak hajnali álmainkban láthattuk,
megérkezett az első űrszonda-felvétel.
Még nem elég éles a felbontása, még
nem tudjuk igazán, mit látunk rajta, de a kezdet
bíztató, idővel úgy fogjuk ismerni
ezt az egzotikus vidéket, mint a tenyerünket.
«»
Marx Gyurkának, akinek
előbb könyvéből (első kiadás!),
majd egyetemi előadásából a kvantummechanikát
tanultam, szeretettel ajánlom ezt a dolgozatot hetvenedik
születésnapjára, amely - ha őrá
nézünk, tudjuk - a legmegfelelőbb életkor
fontos új vállalkozások megalapozására.
Irodalom
E. SCHRÖDINGER: Die gegenwärtige
Situation in der Quantenmechanik - Naturwissenschaften 23
(1935) 807-812, 823-828, 844-849.
A. ZEILINGER - személyes
közlés (1995)
D.M. GREENBERGER, M.A. HORNE,
A. SHIMONY, A. ZEILINGER: Bell's theorem without inequalities
- Am. J. Phys. 58 (1990) 1131-1143
W. ZUREK: Decoherence and
the transition from quantum to classical - Physics Today 44
(1991 október) 36
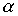 -részecskét detektál egy
számlálócső, amelyhez csatlakozó
szerkezet összetör egy méreggel teli fiolát
[1]. Amíg az
-részecskét detektál egy
számlálócső, amelyhez csatlakozó
szerkezet összetör egy méreggel teli fiolát
[1]. Amíg az 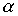 -részecske a magba bezárva marad,
a macska él. Mivel az
-részecske a magba bezárva marad,
a macska él. Mivel az 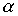 -bomlás alagúthatással
történik, ami a legtipikusabb kvantummechanikai jelenségek
egyike, világos, hogy az
-bomlás alagúthatással
történik, ami a legtipikusabb kvantummechanikai jelenségek
egyike, világos, hogy az 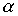 -részecske tulajdonképpen
a magba zárt és a magból kiszabadult állapot
szuperpozíciójában van. Ha elfogadjuk, hogy
a kvantumelmélet a világ minden dolgainak elmélete,
akkor a szuperpozíció nem csak az
-részecske tulajdonképpen
a magba zárt és a magból kiszabadult állapot
szuperpozíciójában van. Ha elfogadjuk, hogy
a kvantumelmélet a világ minden dolgainak elmélete,
akkor a szuperpozíció nem csak az 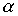 -részecskére,
hanem a macska és az
-részecskére,
hanem a macska és az 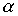 -részecske együttesére
is vonatkozik, legalábbis addig, amíg rá
nem nézünk a macskára és élőnek
vagy döglöttnek nem találjuk.
-részecske együttesére
is vonatkozik, legalábbis addig, amíg rá
nem nézünk a macskára és élőnek
vagy döglöttnek nem találjuk.