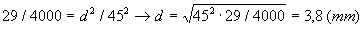Fizikai Szemle 1998/5. 168.o.
MAGFIZIKAI KÍSÉRLETEK 14 ÉVES TANULÓKNAK
II.
Sebestyén Zoltán
Testvérváros-téri
ált. isk., Pécs
A toron bomlástermékeinek kimutatása zárt
elektroszkóppal
A kísérlet előtt körülbelül
4 óráig tegyük a negatív töltésű
(golyóstollkupakkal ellátott) elektroszkópon
levő, felül nyitott konzervdobozra a gázharisnyát,
erre a kartonlapot. Óránként ismét
töltsük fel a sugárzás hatására
csökkenő potenciálú elektroszkópot.
(Ezt óraközi szünetekben megtehetjük.)
4 óra elteltével ismét töltsük
fel az elektroszkópot a 35. skálaértékig.
Helyezzük rá a tóriumharisnya nélküli
kartonlappal lefedett konzervdobozt. A korábban tárgyaltak
szerint a besugárzás után a konzervdoboz
zárt terében (zömmel a kupakon) csak a kiáradó
toron nemesgáz bomlástermékei maradtak. (A
torongáz gyakorlatilag nem, mert le kellett emelni a dobozt
az elektroszkópról, hogy feltölthessük,
így ami még benn maradt, az is elillant.)
A leányelemek bomlásánál keletkezett
sugárzás ionizáló hatására
csökkent a zárt elektroszkóp töltése.
Ezt mutatta a torongörbe a korábbi számban
(34. oldalon) megjelent ábrázoláson.
Ködkamrás kísérletek
Gyári ködkamrával végezhető
kísérletek
A Wilson-féle ködkamra iskolai használatra
készült egyszerű, szovjet gyártmányú
változatát a 8. ábra mutatja. A kamrába
gyárilag be van építve egy 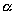 -sugárforrás.
Ebbe 1-2 cm3 szeszt vagy metilalkohol
50 %-os vizes
oldatát, vagy egyszerűen desztillált vizet
csepegtetünk a szívócsonkon át. Ezután
körbeforgatjuk néhányszor, hogy a folyadék
jól szétterüljön az oldalfalán
(nem az ablakokon, hanem a paláston).
-sugárforrás.
Ebbe 1-2 cm3 szeszt vagy metilalkohol
50 %-os vizes
oldatát, vagy egyszerűen desztillált vizet
csepegtetünk a szívócsonkon át. Ezután
körbeforgatjuk néhányszor, hogy a folyadék
jól szétterüljön az oldalfalán
(nem az ablakokon, hanem a paláston).

A kivezető csőre egy 50 cm3-es benyomott
dugattyújú orvosi fecskendőt kell csatlakoztatnunk.
Ez aránylag nagy fecskendő, de fontos a mérete.
Néhány percet várunk, míg a belső
tér telített lesz gőzzel, majd körülbelül
300 voltos tisztító egyenfeszültséget
kapcsolunk rá.
A ködkamra térfogata közel 100 cm3.
A gumicsőbe körülbelül 10 cm3
levegő fér, így az eredeti térfogat
110 cm3. Kihúzott dugattyúnál
150-160 cm3 lesz az együttes térfogat,
ez éppen megfelelő térfogatarányt
ad, (V2 / V1 ~ 1,4) mert
ekkor a dugattyú gyors kihúzásakor -10 °C
és -15 °C közti hőmérséklet
alakul ki egy-egy pillanatra a kamrában. Ezen a hőmérsékleten
már olyan lesz a túltelített gőz a
belső térben, mely az 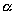 -sugárzás által
létrehozott ionsorra csapódik ki, láthatóvá
téve a részecske pályáját.
-sugárzás által
létrehozott ionsorra csapódik ki, láthatóvá
téve a részecske pályáját.
A látvány csak 1-1 másodpercre élvezhető,
ezért ismételni kell az expanziót. A ködfonalak
jobb láthatósága érdekében
a kamra alá fekete lapot teszünk, és oldalról
megvilágítjuk például kompakt lámpával.
Azért praktikus e lámpa, mert fényereje eleve
nagy, és nem melegít számottevően
akkor sem, ha néhány cm-re van a kamrától.
A ködfonalakat csak sötét háttér
és oldalsó világítás esetén
láthatjuk, ezért írásvetítővel
nem vetíthető ki, de videokamerával jól
felvehetők.
A 200-300 V tisztító egyenfeszültségre
azért van szükség, mert a kamrában állandóan
keletkező ionokat az elektromos erőtér eltávolítja.
Az ionok a porra is rá tudnak csapódni, s így
a töltött porrészecskéktől is megtisztítja
a belső légteret a villamos erőtér
azáltal, hogy ezeket a megfelelő elektródához
vonzza. Így por- és ionmentes túltelített
gőztér áll rendelkezésünkre az
expanziókor.
A preparátumból éppen kirepülő
és maga után friss ionsort hagyó részecske
pályája mentén az expanzió pillanatában
létrejön a kondenzcsík. Ez hasonló ahhoz,
mikor nagy magasságban a repülőgépek
kondenzcsíkot hagynak maguk után. (Ott persze a
hideg, túlhűtött tiszta levegőben lévő
vízpára az égéstermék apró
füstszemeséire csapódik ki.)
Ha nincs ilyen feszültségű áramforrásunk,
akkor néhány olcsó alkatrészből
könnyen összeállíthatunk egyet magunk
is.
Egyszerű, házilag elkészíthető
300 voltos egyenfeszültségű áramforrás
Az alkatrészek jegyzéke: 3 db 1 Mohm fél wattos
ellenállás;1 db 50 Kohm fél wattos ellenállás;1
db 1N4007-es, vagy BA159-es dióda;1 db 0,1 µF-os és
legalább 300 V átütési feszültségű
blokkkondenzátor; 1 db villásdugó; 2 m kéteres
vezeték; 1 db műanyag szappanos doboz; 6 x 4 cm2-es
kartonlap, vagy nyáklap.
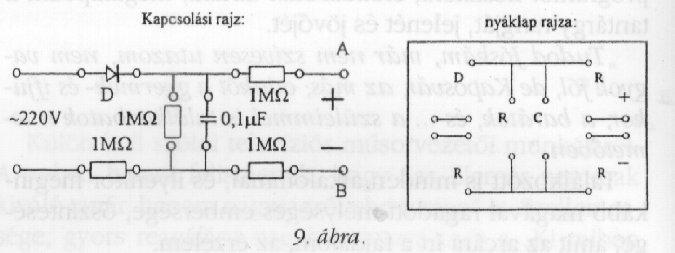
Az összeállítás
teljesen biztonságos a millióohmos védőellenállásoknak
köszönhetően (9. ábra).
Ugyanis a 300 V körüli egyenfeszültség hatására
a 2 Mohm-on keresztül még az AB pontok rövidre
zárása esetén is csak igen kicsi, I ~ 0,1 mA
erősségű áram folyik. Így akkor
is veszélytelen az előállított feszültség,
ha a AB pontokat kezünkkel egyszerre megfogjuk!
Fontos, hogy a kamra légmentesen legyen lezárva,
mert ellenkező esetben az expanziónál külső
por is kerülne a kamrába, és így arra
csapódna ki a gőz.
Házi készítésű expanziós
ködkamra
Az általános iskolákban nem szokott lenni
gyári ködkamra, mert az atomfizika nem volt tananyag,
de magunk is készíthetünk az iskolában
zömmel már meglévő eszközökből,
és anyagokból. Jeges professzor ezt írta
erről: "Az egyszerű expanziós ködkamra
elkészítése sem igényel különösebb
kézügyességet. Működtetése
azonban olyan élményt jelent, ami nagyon megéri
a ráfordított időt és fáradságot.
Lehetővé válik általa egyetlen atommag
helyének, mozgásának megfigyelése.
Magát az atommagot (a He atomjának magját)
- mely az atomnál is körülbelül 105-ször
kisebb átmérőjű, rendkívül
nagy sűrűségű anyagi részecske
- természetesen nem láthatjuk (és mai tudásunk
szerint soha nem is lesz látható), de pályáját,
melyen az előző néhány század
vagy tized másodpercben elképzelhetetlenül
nagy sebességgel (15-20 000 km/s) végigszáguldott
már kényelmesen megfigyelhetjük.
A ködkamrát a tanulói hőtani készlet
25 cm3 térfogatú Erlenmayer-lombikjából
készíthetjük el a legkönnyebben. További
eszközök és anyagok: lombikba illő gumidugó
(a dugó kisebb átmérője 20 mm);
2 x 10 cm hosszú 1-1,5 cm átmérőjű
fémdrót; szemcseppentő üvegrésze;
fél méter hosszú 10 mm2-es
keresztmetszetű villanyvezetékről lehúzott
műanyagcső; 2 x 2 cm2 felületű
itatóspapír; gázharisnya 2 x 3 cm2-es
darabja; 2 db műanyag orvosi fecskendő (10 és
20 ml-es); kevéske denaturált szesz és desztillált
víz.
A ködkamra elkészítésének menete:
A gumidugót középen fúrjuk ki glicerinbe
mártott 4 mm átmérőjű dugófúróval.
Ha ez nincs, akkor- izzó 4 mm-es csavarral vagy szeggel
is kifúrhatjuk. Fontos, hogy a furatba szorosan illeszkedjen
a szemcseppentő 6 mm átmérőjű
csöve. Még egy vékony forró szeggel
a dugóba átellenesen két kis furatot kell
készíteni, melybe az 1-1,5 mm átmérőjű
huzalt kell majd beledugni úgy, hogy a dugó alján
körülbelül 6 cm-t érjen túl.
Fontos, hogy a dugó a furataival együtt légmentesen
zárjon!
Ha nincs üveg szemcseppentőnk, akkor egy 6 mm átmérőjű
üvegesőből vágjunk le egy 12 cm
hosszú darabot. (Az üvegcsövet elvágni
úgy kell, hogy tűreszelővel bekarcoljuk, majd
kettétörjük.) Az üvegcső közepét
gázlángban lágyulásig melegítve
körülbelül 2 cm-t széthúzzuk.
Az elvékonyított résznél az előbb
leírtak szerint ketté vágjuk. Az így
elkészült szemcseppentő végeit gázlángban
lágyulásig melegítve az éles részeket
letompítjuk legömbölyítjük.
A dugóban levő drótok külső
végeit kúpos fogóval körbehajtjuk (körülbelül
4-5 mm átmérővel) hogy a banándugó
beleférjen. Ezután a drót alsó végeit
kissé széthajtjuk úgy, hogy a lombik oldalfalával
párhuzamosan álljanak. A dugóba nyomjuk bele
a szemcseppentőt a vastagabb részével lefelé.
Ha ez nehezen menne, akkor az üvegcsövet egy kis szappanos
vagy mosószeres vízzel tehetjük síkossá.
Így könnyen benyomhatjuk a dugó szűk
furatába. A cső a dugó alsó részén
épp hogy túlérjen (10. ábra).

A lombikba a 2 x 2 cm2 méretű
itatóspapírt tegyük be úgy, hogy ferdén
tartva a lombik oldalára kerüljön. Néhány
csepp desztillált vizet csepegtessünk a lombikban
lévő itatóspapírra. Nyomjuk kissé
az itatóst a lombik falához, mely ettől odatapad.
(A desztillált víz azért kell, hogy az elpárolgó
víz ne hagyjon foltot az edény falán.)
Néhány (5-10) csepp metilalkoholt is tehetünk
a lombikba. Tapasztalatom szerint így a legerőteljesebbek
a ködfoltok. A folyadékokból többet is
önthetünk, de felesleges, mert nem lesz szebb a látvány
tőle.)
Ezután tegyük be a körülbelül 2 x 3 cm2
méretű gázharisnya-darabot a lombik aljára.
Szükségünk van egy fél méter
hosszú 3-4 mm közötti belső átmérőjű
műanyag- vagy gumicsőre. Ez lehet egy műanyag
szigetelésű 10-es villanyvezetékről
lehúzott műanyagcső is. Természetesen
kiválóan alkalmas erre a célra az infúzió
átlátszó műanyagcsöve is. A cső
egyik végét a ködkamra dugójából
kiálló szemcseppentő szűkített
végére óvatosan rányomjuk. A másik
végét a 20 cm3-es benyomott dugattyújú
fecskendő csőcsonkjára húzzuk.
A gumidugóból ki- és szétálló
drótvégeket kissé összenyomva behelyezzük
a lombikba, majd a dugó beszorításával
hermetikusan lezárjuk az üveget.
A fecskendő a lelke az egész ködkamrának.
Kipróbáltam többféle lehetőséget
(átalakított, megfordított bőrözésű
kerékpárpumpát, különböző
méretű és szerkezetű Orvosi fecskendőket,
légszivattyút, hűtőgépkompresszort,
matracpumpát stb.). A legpraktikusabb, legegyszerűbb
és egyben legolcsóbb megoldás az eldobható
egyszer használatos orvosi fecskendő. Ennek több
fajtája létezik. Az a jó fecskendő,
amelyiknek a dugattyújába bele van pattintva a dugattyú
nyomókarja (ekkor a kart könnyen körbe lehet
forgatni a fecskendőtől függetlenül).
Az ilyen dugattyút tapasztalatom szerint könnyű
mozgatni, ugyanakkor hermetikusan zár kihúzáskor
és benyomáskor egyaránt. A fecskendő
végét befogva próbáljuk ki mindkét
irányba. A kísérleteinkhez kiválóan
alkalmas például a Mátraplast által
gyártott QUADPROJECT elnevezésű egyszer használatos
biztonsági fecskendő. Érdemes 10- és
20 ml-est beszerezni, mert mindkettővel elvégezhető
a kísérlet.
Ha a korábban leírt egyenáramú áramforrást
már megépítettük, akkor kapcsoljuk rá
a ködkamrára a 300 V tisztító-egyenfeszültséget.
A kísérlet a ködkamra teljes összeszerelése
után néhány perccel már el is kezdhető.
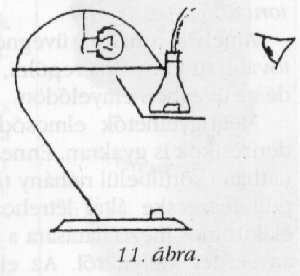
Ezután állványba fogva a ködkamrát,
kompakt lámpával, vagy íróasztal-lámpával
a 11. ábra szerinti módon megvilágítjuk.
A kontraszt miatt fekete háttérre feltétlenül
szükség van.
Érdemes megfigyelni, hogy tisztító feszültség
nélkül csak köd keletkezik, és igen ritkán
ködfonal - ugyanis a mindenfelé jelenlévő
ionokra és lebegő szennyeződésekre
rögtön ki tud csapódni a bent levő pára.
Ha a dugattyút gyors mozdulattal meghúzzuk, és
közben végig figyeljük a ködkamrát,
akkor pár pillanat múlva a keletkezett köd
apró vízcseppjeinek lassú zuhanását
is láthatjuk rövid ideig. Ezután nyomjuk vissza
a dugattyút a benyomott alaphelyzetbe.
Megismételhetjük az expanziót lassabb kihúzással
is. Ekkor kevesebb köd képződik, még
lassabb kihúzásnál már nem képződik
köd. Nem árt e mozdulatokat - a dugattyú mozgatását
begyakorolni. Úgy érdemes húzogatni a dugattyút,
hogy a ködképződés határát
eltaláljuk, mert ilyenkor csak a részecske ionizált
nyomvonala mentén jön létre a ködképződés.
Így jobban láthatók a ködfonalak.
Azt is jól megfigyelhetjük, hogy mikor a dugattyút
visszanyomjuk - a ritkítást megszüntetjük
(a levegőt sűrítjük) -, a ködszemcsék
elpárolognak (a belső tér ekkor kicsit felmelegszik
és kitisztul). A későbbi expanziók
között 2-3 másodpercet várnunk kell miután
visszanyomtuk a dugattyút.
Néhány expanzió után - de lehet,
hogy az elsőre is már izgalmas, csodálatos
látványban lesz részünk. Finom kis cérna
vékonyságú ködfonalak tűnnek fel
a belső térben és múlnak el, foszlanak
szét változó alakkal, lassú süllyedés
közben. Néha több is látható egyszerre,
de van sokszor, hogy több expanziónál egyet
sem látunk. Ez így természetes, ugyanis a
radioaktív bomlás statisztikus jellegű, másrészt
a gázharisnya a tér minden irányába
lő ki részeket, de ezeket csak egy kis térszögben,
tér részben tudjuk kimutatni, láthatóvá
tenni.
Ha régebben (pár napja) tettük be a gázharisnyát,
akkor észrevehetően nem csak a harisnya irányából
indulnak ki a ködfonalak, hanem olykor akár vele
párhuzamosan, vagy lefelé, jelezve az emanáció
jelenlétét. A toron nemesgáz rövid élete
alatt szétdiffundált, majd leányelemei a
lombik belső falára tapadtak. Az észlelt
más irányú ködfonalakat az ezekből
kiinduló sugárzás idézte elő.
Természetesen nem lehet előre megjósolni,
kiszámítani, hogy hol és melyik pillanatban
mennyi sugár jön létre a radioaktív
tórium-sor bomlásakor - ez is bizonyítja,
hogy statisztikus jelenség a radioaktív bomlás.
Alaposan megfigyelve a jelenséget, látható
hogy az expanzió pillanatában még egyenes
ködfonalak később elgörbülnek. A
fonalakat alkotó apró vízcseppekre az elektromos
tér nem hat észrevehetően úgy, mint
az ionokra. A légáram és a gravitáció
annál inkább, ezért görbülnek el
és süllyednek.
Megfigyelhető, hogy a fonalak hossza különböző,
és sokszor az egész rövid 1-2 cm-es fonál
erőteljesebb, vastagabb. Van, hogy a fonál nyílegyenesen
az üvegnél végződik, de a ködfonalak
legtöbbször a belső térben végződnek.
A látható hosszuk néhány mm-től
6 cm-ig (a lombik maximális belső méretéig)
terjed. (Talán a zömük 3-5 cm közé
esik.)
Az erős rövid fonalak nem a harisnya felszínéről,
hanem mélyebbről (körülbelül századmilliméter
mélységből) származnak, s így
az -részek a levegőbe már sok-sok atommal
való ütközés után lelassulva, kisebb
kinetikus energiával lépnek ki. Ezek centiméterenként
több ionpárt hoznak létre - ezekre több
vízgőz tud kicsapódni -, vastagabb a ködfonal.
Megfigyelhető ez egyébként minden elhaló
ködfonálnál is, a végei mindig kicsit
vastagabbak. A sebesség csökkenésével
az ionizáló képesség nő!
Amelyik fonál az üvegnél végződik,
az levegőben nyilván tovább tudott volna
repülni, és ionizálva ködfonalat létrehozni,
de az üvegben elnyelődött.
Megfigyelhetők elmosódott szalagszerű halványabb
kondenzcsíkok is gyakran. Ennek oka lehet az expanzió
előtti pillanatban (körülbelül néhány
tized másodperccel korábban) elrepült részecske
által létrehozott ionok diffúziója,
és hogy az elektromos mező hatására
a térben néhány mm-re eltávolodtak
az eredeti helyükről. Az ekkor létrehozott
expanziónál már ezekre csapódott le
a gőz - szélesebb, halványabb ködszalag
alakult ki.
Érdekes a 10 ml-es fecskendővel is elvégezni
a kísérletet. A fecskendő cseréjét
mindig benyomott dugattyúnál végezzük,
majd néhány expanzióval átöblögetjük
a rendszert. Nagyon gyors, hirtelen rántásra nem,
vagy csak alig látható, igen gyenge a ködképződés.
Ez természetes is, hiszen itt körülbelül
négy a térfogatarány, melynek megfelelően
csak körülbelül 10 C-kal hűlt le expanziókor
a belső tér, és így kevésbé
túltelített a levegő.
Ha a ködkamrát a 10 ml-es fecskendővel működtetjük,
és igen gyorsan húzzuk ki a dugattyút, akkor
látható köd nem képződik ugyan
az egész belső térben, de azért a
nagyobb fecskendőnél lévő ködfonalakhoz
képest vékonyabb, fényszegényebb ködfonalak
létrejönnek a sugarak nyomán.
Ha a ködkamrába víz helyett alkohol és
víz 50%-os keverékét tesszük, alapvető
eltérést nem lehetett észrevenni a kamra
működésében. Talán ekkor egy kicsit
jobban láthatók a ködfonalak.
Ha csak alkohol volt a ködkamrában, akkor a 20 ml-es
fecskendő dugattyúját nem kellett olyan gyorsan
kihúzni, mint a többi esetben.
Szárazjeges diffúziós ködkamra
A Sopronban megrendezett Alkotó Fizikatanítás
Nemzetközi Konferencián sok ötletes és
újszerű kísérletet mutattak be a japán
fizikatanárok. Ezek között volt egy igen egyszerű
diffúziós ködkamra, melyben sokkal jobban és
tovább láthatók az ionizáló
részecskék hatása révén létrejött
ködfonalak, mint az expanziós ködkamrában.
Az eszközt Mori Yuji tokiói fizikatanár
készítette és Tóth Eszter (Budapest,
Lauder Iskola) kapta meg ajándékba, így nála
lehet megtekinteni (12. ábra).
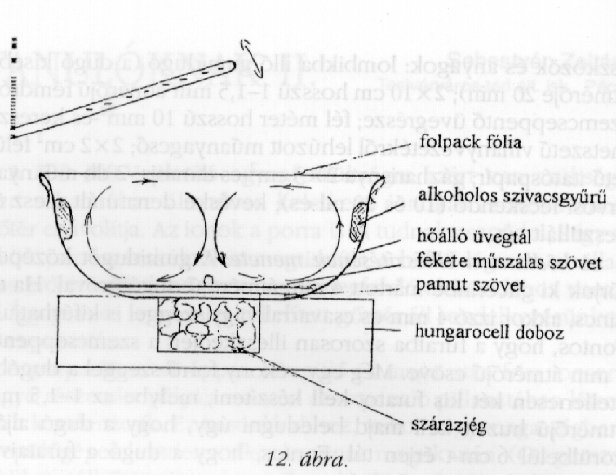
Ha valaki tud szárazjeget (szilárd széndioxidot)
szerezni, akkor körülbelül 1 kg-mal könnyen
elvégezheti a kísérletet a rajz szerinti
összeállításban. Fontos, hogy középen
hűtsük az edényt, a légáramlás
(cirkuláció) miatt. A páradús, telített
levegő középütt lefelé áramlik,
s egyre jobban lehűtve túltelítetté
válik, így e közegben folyamatosan létrejön
a kondenzáció az sugarak nyomán.
A tisztító feszültséget egy megdörzsölt
(negatív töltésű) műanyagrúddal
biztosíthatjuk, melyet időnként a fólia
fölé kell közelíteni. Igen szép
és látványos a kísérlet!
Mi van az atomok belsejében?
Milyen az atomok belső felépítése?
Rutherford kísérletének golyós
modellezése
A kísérlet összeállítása:
A mechanikai tanulói kísérlet golyógurítójára
ragasszunk egy körülbelül 5 x 10 cm2-es
műanyag, vagy fémlapot, hogy segítségével
a golyókat mindig egymással párhuzamosan
guríthassuk.
Egy 2-3 cm átmérőjű gumidugót
középen forró szeggel lyukasszunk ki, és
egy átmenő csavarral fúrógépbe
fogva, durva csiszolópapírral a rajz szerinti alakra
csiszolunk. Ezután körülbelül 20 cm átmérőjű
kartonlappal fedjük le a gumidugót, majd egy hosszabb
átmenő csavar segítségével
egy sima felületű (például laminált)
körülbelül 30 x 30 cm2
forgácslemez lapra rögzítjük.
A korong az atomnak, a golyó az a-résznek felel
meg. Akkora golyót válasszunk, mely a friss indigó
felett levő vékony fehér papírlapon
végiggurulva nyomot hagy, de a korong alatt el tud gurulni!
A méretarányok erősen torzítottak,
hiszen ha az atommagot cseresznye méretűnek vesszük,
akkor az atom stadion méretű kéne legyen.
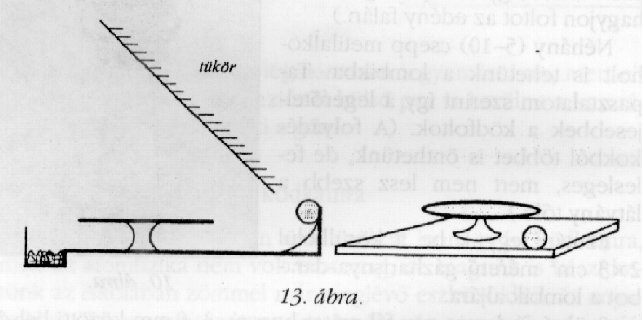
A tanulók egy körülbelül 45°-os
szögben a gurítópálya fölé
helyezett tükörben felülről láthatják
a modellkísérletet. A golyót és a
"gombát" (atomot jelképező korongot)
egy elöl lévő takarás miatt nem láthatják
oldalról a tanulók - csak felülről a
tükrön keresztül (13. ábra).
Így a golyó pályáiból kell
megállapítaniuk a gyerekeknek, hogy a korong tömör,
vagy csak középen az!
A korong melletti és a korong szélei alatti átgurulás
változatlan irányú. Beljebb különböző
irányú a visszapattanás. A modell, a 13-14
éves gyerekekkel is megsejteti a szórási
kísérlet lényegét - az atom nem tömör,
nem jó a görögdinnye modell, a nukleonok nem
elszórva vannak az atomban, hanem a kis térfogatú
atommagban vannak tömörülve.
Egy ilyen gurítási sor indigós nyomvonal
részletét mutatja a 14. ábra.

Izgalmasabb a kísérlet, ha a tanulók együttes
kockadobással adhatják meg véletlenszerűen
a golyó indulási helyét. Például
14 tanuló 3-3 dobókockával rendelkezik. Mindenki
dob a dobókockáival, ezek értékét
összeadják, és a gurítópálya
arra a helyre fog kerülni a milliméter skálán
(ez minimum 42 mm, és maximum 252 mm). Ugyanígy
kapjuk meg az újabb indítás helyét.
Minden egyes gurítás egy-egy résznek felel
meg. A guruló golyót a széleken körbe
terített sállal fogjuk fel.
A valóság Coulomb-taszítását
itt a rugalmas ütközés helyettesítette,
mely természetesen más, de ez első közelítésben
nem zavaró, a dolog lényegét nem érintette.
Még az sem zavarta a megértést, hogy némelyik
gurítás nem sikerült párhuzamosra, sőt
valósághűbb lett a modellkísérlet,
hiszen a részecskék között is lehetnek
más mozgásirányúak.
A Rutherford szórási kísérletének
sörétgolyós modellje
A Szűcs-munkafüzetben erre vonatkozóan a következő
kísérletek és feladatok szerepelnek:
- " Vegyünk egy lecsavarható, műanyag
fedelű dobozt (például a neszkávés
dobozt, vagy nesquikes kakaós dobozt). A doboz tetején
fúrjunk forró szöggel kis kerek, körülbelül
5 mm átmérőjű lyukat. Helyezzünk
a dobozba 20 sörét- vagy borsszemet, melyek a fürt
lyukakon át tudnak esni. Hirtelen mozdulattal fordítsuk
a feje tetejére tízszer egymás után
a dobozt! Számláljuk meg a kiesett szemeket. . ."
- " Vegyük úgy, mintha 1 szem próbálkozott
volna a lyukakon való kijutással 20 x 10 = 200
alkalommal. A kiesett szemek száma pedig jelzi, hogy hányszor
járt eredménnyel a kijutás. Ezért
osszuk el a kijutott szemek számát az összes
(200) próbálkozással, így megkapjuk
a kijutási esély arányszámát.
. ."
- A fedél- és lyukátmérő
négyzeteinek aránya és a sörét
kiesési esélyek aránya közti kapcsolat
vizsgálata.
Érdemes a kísérletet különböző
területarányú, de azonos sörétszámú
modellekkel elvégezni. Ez a kísérletsor
is fontos ahhoz, hogy a diákok ráérezzenek
az eredeti Rutherford-kísérlet értelmezésére
és szépségére.
Persze itt a modellnél pont fordított a dolog.
Ahol a sörét kijön - ahol a modellnél
lyuk van -, ott a valóságban levő szórási
kísérletben épp az atommag van. Maga a hengeres
doboz teteje viszont megfelel egy atomnak.
Fontos! A borítgatásokat be kell gyakoroltatni
a mérés előtt, nehogy a sörétek
(20 db) a doboztető széle felé, egy kupacba
essenek, rossz eredményt adva. Arra kell ügyelni,
hogy függőleges helyzetből - függőlegesen
fordított helyzetbe - úgy forgassuk át a
hengert, hogy a forgatás alatt lehetőleg már
szinte súlytalanok legyenek a "sörétgolyók"
(azaz ne érjenek már az edény felülre
került alsó lapjához). Ezt úgy érhetjük
el, hogy először a függőleges helyzetű
vízszintes alaplapú hengert felfelé gyorsítjuk,
majd a fenti leállás közben fordítjuk
meg és indítjuk lefelé a hengert. (Ekkor
a szabadon eső sörétek körül fordul
a henger. A véletlen szórás realitásának
így van legnagyobb esélye, valamint annak is, hogy
a golyók ne egy kupacba legyenek. )
A Nestlé-Nesquik kakaós dobozok közül
a 200 g-os , ~70 mm átmérőjű
és 400 g-os ~100 mm-es könnyen - akár
egy forró csavarral, vagy az iskolai dugófúró
készlet fúrójával - kifúrható
tetővel készül. Ha a 70 mm-es tetőn
5 mm-es lyukat fúrunk, akkor a lyuk és tető
területaránya, azaz a két átmérő
arányának négyzete 1/200. Ha a ~100 mm
átmérőjű tetőt 10 mm, 7 mm,
vagy 5 mm átmérőjű furattal készítjük
el, akkor a területarányok - rendre 1/100,1/200,1/400
értékűek.
Mindegyikbe 20-20 sörétgolyót téve,
20 borítás összesen 400 sörétpróbálkozásnak
felel meg a lyukon való kijutást tekintve.
A kijutott sörétek számának és
az összes próbálkozásnak a hányadosait
összehasonlítva a területarányokkal -
sok esetben kapunk egyező eredményt, vagy megközelítő
értéket.
Lyukátmérő meghatározása
sörétszórással
A tapasztalatok kiértékelése után
került sor az izgalmas feladatra: egy neszkávés
doboz ismeretlen lyukátmérőjének meghatározására
sörétszórással (15. ábra).

A gyerekek "biztosra" akartak menni, 200 borítást
szavaztak meg. Ez körülbelül negyed óráig
tartott.
Fontos megjegyzés: A borítgatás során
kiesett sörétet mindig vissza tettük a neszkávés
dobozba, hogy, mindig 20 söréttel menjen a kísérlet!
A borítgatást egy nagyobb papírdoboz (30x40
cm) felett végezték. Így a kieső sörét
koppanását mindenki jól hallotta, és
a sörét nem tudott elgurulni, ezért gyorsan
vissza lehetett tenni.
A 200 borítás 4000 próbálkozásnak
(-sugárnak) felelt meg. Ez alatt 29 sörét (atommagról
visszaverődő -részecske) esett ki a lyukon.
A kávés doboztető (atomátmérő)
45 mm volt.
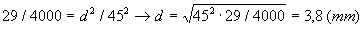
A lyuk átmérője a valóságban
4 mm volt! Ismételt kísérletnél 27
sörét esett ki, így 3,7 mm adódott a
lyuk átmérőjére. A lyuk becslési
pontatlansága tizedmilliméteres nagyságrendbe
esett!
A láncreakció és reaktor gyufás
modellezése
A hírhedt piramisjátékokat szinte minden
gyerek ismeri. Ehhez hasonló folyamatot nem nehéz
megértetni a tanulókkal. Sokan ismerik a legenda
szerinti sakkozó történetét is, ki az
uralkodótól győzelméért "csak"
annyi búzaszemet kért, amennyi a sakktábla
első mezőjére tett egy szem induló
és minden további mezőn megduplázott
búzaszemekkel adódna. A 64. mezőre a világ
összes búzatermése sem lenne elég!
A láncreakció is hasonló folyamat. A szabályozatlan
és szabályozott láncreakció gyufás
modellel szemléltethető. A szabályozott láncreakció
síkbeli gyufás modelljét a fénykép
mutatja (16. ábra). A 15x25 cm2 méretű
alumínium lapra 5 sorban 1, 2, 4, 8, és 16 lyukat
(2 mm átmérőjű) fúrunk a kép
szerint. A furatok éles széleit 5 mm-es fúróval
kissé leperemezzük. Így könnyebben lehet
a gyufaszálakat befűzni. A gyufaszálakat vastagabb
pamut fonállal kötjük össze először
szabályozatlan, majd a szabályozott modellnek megfelelően.
Szűcs József írja erről:

"A láncreakció beindítása
úgy történik, hogy a gyufafejek közötti
fonálszakaszokon borszesszel (Vigyázat nem robbanó
anyaggal, például benzinnel!!!) ecset segítségével
átitatjuk, majd az első gyufafejet meggyújtjuk.
Ekkor a gyufafejek begyulladása szabályozatlan vagy
szabályozott formában láncreakciót
modellezve történik. Megjegyzés: Vigyázzunk
a kísérlet TŰZVESZÉLYES!! Célszerű
a fémlapot egy nem éghető tálca felett
Bunsen-állványon rögzíteni függőleges
síkban úgy, hogy az első gyufafej felül
legyen. "
Ügyeljünk arra, hogy a nem éghető (tálca)
lap ne legyen nedvszívó sem (például
palalap vagy fémlap) és az esetleg elcsöppent
szeszt töröljük fel, valamint az ecsettel történő
denaturált szeszes átitatáskor ne kerüljön
a fonalak mellé alkohol. Az alkoholos üveget zárjuk
le, az ecsetet is tegyük távolabb. Csak ekkor gyújtsuk
meg a bevezető szálat, mely majd beindítja
az első "maghasadást" jelképező
1. gyufafej belobbanását. A lapot kissé ferde
helyzetben tartva (tehát ne teljesen függőlegesen)
a tanulók végig jól láthatják
(és élvezhetik) a látványos tűzijátékot,
melynek végén, ha elég ügyesek vagyunk,
mind a 16 gyufa belobban. A kísérlet után
szellőztessünk!
LED-es láncreakció modell
A kísérleti modell elektronikus változatát
Szűcs tanár úr készítette el.
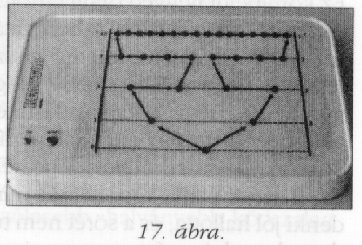
Itt gombnyomással indítjuk a LED sort a szabályozatlan,
és szabályozott láncreakciónál
(17. ábra).
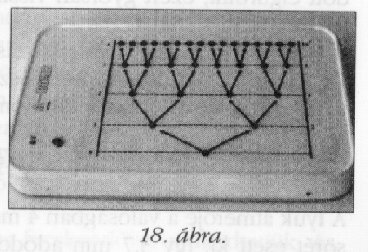
A szabályozott modellnél a világító
diódák közül mindig csak kettő,
a szabályozatlannál pedig kettő hatványai
szerint növekvő számú világít
(18. ábra).
A modell megtekinthető Szűcs Józsefnél
(Pécs, JPTE Fizika Tanszékén).
Ismerjük meg környezetünk sugárzásait!
A Szűcs-munkafüzet dobókockás kísérlete
elé a radioaktivitás valószínűségi
törvényének szemléltetésére
Marx György: "A természet játékai"
című könyvében olvasható több
érdekes játék közül a legegyszerűbbet
javasolom és idézem:
"Dobjunk egyforma pénzérméket
egy dobozba, azután a becsukott dobozt erősen rázzuk
meg. Ezután eltávolítjuk az összes "fej"
helyzetű pénzt. Újra megrázzuk. A fejeket
ismét eltávolítjuk. És így
tovább, sokszor egymás után. (Ha például
a rázások percenként követik egymást
a pénzérmék száma T =1 perc felezési
idővel csökken. A statisztikus ingadozásoktól
eltekintve N = N0/2T. Egy
tárgyi modell alapján szembeszökő, hogy
a pénzérmék nem öregszenek. Úgy
viselkednek, mint egy mesebeli város polgárai, ahol
nincs születés és nincs betegség, a
létszámot csak véletlen közlekedési
balesetek apasztják.) "
Ez a játékos kísérlet azért
tetszett meg, és ajánlom másoknak is, mert
a szakköri foglalkozáson általában kevés
gyermek van (12 körül szokott lenni), és ha minden
gyerek egy pénzérmével játszik, úgy
nem érvényesül a statisztikus jelleg. Az új
kisméretű egy- vagy kétforintosból
több százat is bedobhatunk a dobozba!
Egy osztálynyi diákkal (25-30 fő) a bomlás
véletlenszerűségét legegyszerűbben
fejenként 3 pénzérmével játszathatjuk
el. Mindenki három pénzérmét (például
3 db 2 Ft-ost) ráz a kezében és adott jelre
az asztalra borítja. Akinél mindhárom írás,
az feláll (ez jelenti az épp elbomlott atommagot).
Mindenkinek ugyanannyi volt az esélye, mégsem következett
be egyszerre az esemény, és senki nem tudta előre
hogy mikor következik. A megmaradó tanulókkal
(még el nem bomlott atomok) ismételjük a kísérletet
a pénzzel még néhányszor. Mindenki
előbb-utóbb sorra kerül és a végén
elfogynak az ülő tanulók, mint ahogy a természetben
a radioaktív anyag atomjai is előbb-utóbb
mind elbomlanak.
A radioaktív bomlás modellezése kockadobással
Ezután végezhetjük el a kockadobásos
modellezést a Szűcs füzet szerint. "A
radioaktív magok bomlásának véletlenszerűségét
modellezhetjük számkockák dobásával.
Vegyünk 20-30 darab számozott játékkockát
amelyeket egy dobozba helyezünk, majd a kockákat sík
felületre borítjuk. Az elbomlott magokat például
a 6-os jelű kockákkal modellezhetjük. "
A kockadobásokat táblázatba foglalva az
is megállapítható, hogy mennyi a "dobások
felezési ideje", hogy nyolc borítás
után a kockák körülbelül hányad
része marad meg, és ez körülbelül
mekkora felezési időnek felel meg.
A számítógépes szimulációs
programokat és az ANRI sugárzásmérő
műszerrel való méréseket nem tárgyalom,
mert ezek már komolyabb beruházást igényelnek
és most ezen írásommal az volt a célom,
hogy elsősorban olcsó, sajátkészítésű
eszközöket és kísérleteket gyűjtsek
össze (a teljesség igénye nélkül)
a nukleáris alapismeretek tanításához.
_______________________
A cikk első része megjelent
a Fizikai Szemle 1998/1 számában.
______________________
A kísérleti eszközöket
Öveges József és zömmel Jeges
Károly leírásait alapul véve állítottam
össze, mert ezek a legegyszerűbbek, legolcsóbbak,
meghízhatóan működnek és bárhol
házilag is előállíthatók. (a
szerző)
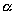 -sugárforrás.
Ebbe 1-2 cm3 szeszt vagy metilalkohol
50 %-os vizes
oldatát, vagy egyszerűen desztillált vizet
csepegtetünk a szívócsonkon át. Ezután
körbeforgatjuk néhányszor, hogy a folyadék
jól szétterüljön az oldalfalán
(nem az ablakokon, hanem a paláston).
-sugárforrás.
Ebbe 1-2 cm3 szeszt vagy metilalkohol
50 %-os vizes
oldatát, vagy egyszerűen desztillált vizet
csepegtetünk a szívócsonkon át. Ezután
körbeforgatjuk néhányszor, hogy a folyadék
jól szétterüljön az oldalfalán
(nem az ablakokon, hanem a paláston).