1. ábra
Fizikai Szemle honlap |
Tartalomjegyzék |
Varga Péter
MTA Műszaki Fizikai és Anyagtudományi Intézet
Szigorúan véve kísérletek nem bizonyítják egy elmélet igazát, hiszen nem zárható ki, hogy létezhet egy másik elmélet, amely szintén tükrözi a tapasztalatot. Alkalmasak viszont arra, hogy cáfolják az elméletet, ha kiderül, hogy ellentmondanak a tapasztalatnak. Mégis, szükség van arra, hogy kísérleteket végezzünk azért is, hogy a tapasztalat segítségével legalább alátámasszuk az elmélet állításait. Különösen akkor van erre szükség, ha ezek az állítások ellentmondani látszanak eddigi tapasztalatainknak, vagy azoknak a megszokásoknak, amelyeket "józan észnek" nevezünk. Jánossy fizikai optikai kutatásai, amelyeket Jánossy-kísérletek néven emlegetünk, ezek közül valók. A kísérletek koruk fizikai kérdéseire kívántak választ adni és végrehajtásuk során az adott kor technikai lehetőségeit használták fel.
Mindenféle kísérlet jelentőségét bizonyítja, hogy azokat a tudományos és a műszaki fejlődés során megismétlik, hogy megbizonyosodjanak a hozzájuk kapcsolódó állítások időtállóságáról, vagy közelítő, esetleg téves voltáról. A Jánossy-kísérleteket megismételték, bár előfordul, hogy magukra az eredeti kísérletekre nem hivatkoztak, egyszerűen azért, mert a kérdések ma is aktuálisak. Ilyen volt a sorsa Selényi Pál nagyszögű interferenciakísérletének is, amit az 1911-ben a kor vezető folyóiratában német nyelven ismertetett, majd egy vita kapcsán a harmincas években megismételt és angolul is leírt [1]. A nyolcvanas években - Selényire nem hivatkozva - mint triviális jelenséget felhasználták [2], végül 1990-ben azt állítva hogy ezt eddig kísérletileg nem mutatták ki, újra megmérték [3]. Az utóbbi munka szerzőinek mentségére szolgáljon, hogy nem ismerték Schrödinger (talán egyetlen) kísérletét [4] sem, aki szintén kimutatta a nagyszögű interferenciát, ő viszont nem tudott az idősebb kortársról.
A kvantumelmélet szerint a fénynek két természete van. Terjedni úgy terjed, mint egy hullám, amelynek jellemzői, például az elektromágneses mező erőssége, vagy ennek négyzete, az energia sűrűsége, folytonos változók. A hullámtulajdonságok az interferencia jelenségében nyilvánulnak meg. Viszont, ha a fény elnyelődik, akkor ugyancsak a tapasztalat szerint, energiája diszkrét kvantumokban lép fel, ezeket a kvantumokat fotonnak nevezik.
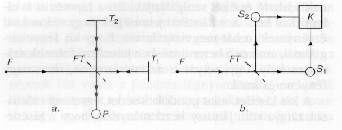
Vizsgáljuk az interferenciát Michelson-interferométerrel
(1.a ábra). Az F fényforrás
fénye egy FT félig áteresztő
tükörre esik, ezen részben visszaverődik,
részben áthalad. (Ennek a jelenségnek a leírására
szükség van a folytonosságot kihasználó
elképzelésre.) A fény mind a két ágban
továbbhalad, majd két tükörre esik, amelyeken
visszaverődik. A visszafelé haladó fény
újra a féligáteresztő tükörre
jut, itt megismétlődik az előző jelenség,
a beeső két hullám most újabb két-két
hullámra hasad.

1. ábra
2. ábra
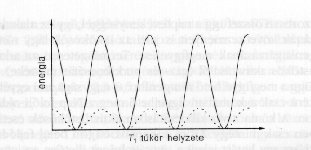
Kövessük most azt a két hullám-részt, amely a T1 tükörről visszaverődve a féligáteresztő tükrön újra visszaverődik és lefelé halad, továbbá azt, amelyik a T2 tükrön verődik vissza, áthalad a féligáteresztő tükrön, ugyancsak lefelé. Ha a P pontban mérjük a fény energiáját, azt tapasztaljuk, hogy ez függ a két tükör helyzetétől. Ha az egyik tükröt önmagával párhuzamosan elmozgatjuk, akkor a mért energia a 2. ábrán látható módon változik, ha a fényforrás sok fényt emittál, akkor az a), ha keveset, akkor a b) görbe szerint. A változás ugyanolyan, csak nagysága különbözik. Ha az egyik tükröt eltávolítjuk, a jelenség megszűnik, a fényenergia nem változik periodikusan. A tapasztalat azt mutatja, hogy a fény mind a két tükörrel kölcsönhatásba lép, a fény a féligáteresztő tükör után egyidejűleg mindkét irányban halad. Tapasztalatunk megegyezik az elméleti várakozással.
Ha a P pontban elhelyezett energiamérőnk olyan, hogy képes a fotonokat számlálni, akkor azt tapasztaljuk, hogy az energiamérő viszont diszkrét kvantumokat jelez. Még kifejezettebb a jelenség, ha az előző interferométerbe a T1, T2 tükrök helyébe S1 és S2 fotonszámlálókat helyezünk (1.a ábra), és kérdezzük, kölcsönhatásba lép-e a fény a két sokszorozóval. A K betűvel jelzett doboz az egyidejű kölcsönhatásokat méri (a továbbiakban koincidenciakísérlet). Az elmélet megjósolja a kísérlet eredményét: a mérés eredménye negatív, a berendezés nem jelez egyidejű kölcsönhatást (egy kis részlettől eltekintve, amelyről alább még szó lesz).
A kvantumelmélet következetes, szabályai szerint másképp kell leírni a két kísérletet, az első kísérletben úgy, hogy a fény mindkét T1 és T2 tükörrel, a másodikban úgy, hogy az S1 vagy S2 mérővel lép kölcsönhatásba. Természetesen mindez az elmélet általános szabályaiból következik, nem pedig az adott kísérlet igazolására szolgáló ad hoc előírásokból. Ugyanekkor ez a kettős viselkedés klasszikus szabályokon nevelődött elménk számára legalábbis furcsa.
Felmerül a kérdés, hogy az elmélet, amely az elektromágneses mező hullámainak fogalmával operál, nem valami statisztikai átlagot ír-e le: a fotonok, amelyek mérésünk objektumai, képezik a valóságot, a folytonos elmélet által adott eredmények csak a fotonok számának várható értékét szolgáltatják. Ezt a hipotézist is ellenőrizni kell. A statisztikai jelenségek nagy számoknál érvényesek, tehát megvizsgálandó, hogy kis fényenergiáknál, amikor a berendezésben jelenlévő fotonok száma csekély, ugyanolyan-e az interferencia, mint nagy fényenergiáknál.
A két kísérlet, mint gondolatkísérlet, egyetemi előadások tárgya volt. Jánossy kezdeményezte, hogy a kísérletek valódiak legyenek [5]. Az interferenciakísérletet Náray Zsolttal [6], a koincidenciakísérletet Ádám Andrással és Varga Péterrel [7] végezte el. Az interferenciakísérletnél két különböző tükörtávolságot használtak, az egyiknél a tükör - féligáteresztő tükör távolság 10-10 cm volt, e körül mozgatták a T2 tükröt, egy másik kísérletsorozatban a távolság 14-14 m volt1. Mérték, található-e különbség az interferenciaképekben nagy és kis energiamennyiségek esetén. Nagy energiáknál egy időpillanatban jóval több mint egy foton energiájának megfelelő energia volt az interferométeren belül, kis energiáknál pedig jóval kevesebb volt az energia átlagértéke, mint egy foton energiája. Az eredmény mindkét kísérletsorozatban negatív lett, az interferenciakép nem függött az energia átlagától.
A koincidenciakísérlet eredménye szintén negatív volt. Pontosabban - mivel egy fizikai mennyiség nemlétét nem lehet kimutatni - a konklúzió az lett, hogy annak a valószínűsége, hogy a két fotonszámláló egyidejűleg megszólaljon, kevesebb volt, mint hat ezrelék.
A két kísérlet bebizonyította az elmélet várakozását, valóban létezik a kettősség. Kissé bonyolította a képet egy nem sokkal a koincidenciakísérlet után megjelent közlemény: mégis vannak koincidenciák.
A csillagok átmérőjét elvben meg lehet határozni egy megfelelő interferométerrel, csakhogy ez a levegő sűrűségének fluktuációi miatt majdnem lehetetlen. Két angol rádiócsillagász, - R. Hanbury Brown és R.Q. Twiss [8] - klasszikus fenomenológiai, nem kvantumelméleti számítások alapján arra jött rá, hogy a rádiócsillagok átmérőjét a koincidanciaberendezéshez hasonló elrendezéssel is mérhetik, ezt a sűrűségingadozások nem befolyásolják. Amikor eljárásukat ki akarták terjeszteni a látható csillagokra is, erről a Jánossy-kísérletre való hivatkozással lebeszélték őket, sikertelenséget jósolva. Mivel a rádióhullámok és a fény egyformán elektromágneses hullámok, az angolok nem adták fel és kísérlettel [9] bizonyították igazukat2.
Ez a tapasztalat nem befolyásolja Jánossy kísérletének konklúzióját, a jelenség oka az, hogy a csillagok, de a földi fényforrások által kibocsátott energia nem állandó, hanem fluktuál, a koincidenciák fellépése ennek tulajdonítható. Ha az eredeti mérést az akkor még fel nem fedezett lézerrel végezték volna el, akkor nem kaptak volna koincidenciákat.
Jánossy kidolgozta a Hanbury Brown és Twiss mérésének nemfenomenológiai elméletét a függetlenül sugárzó atomok által kibocsátott fény fluktuációiról [11]. (Ezt az eredményt említi meg az optikusok bibliájának számító M. BORN, E. WOLF: "Principles of Optics" című könyve. Megemlítendő, hogy a könyvben Jánossy mellett csak két magyar, Petzval József és Gábor Dénes neve szerepel.) Az elmélet alapján Nárayval és Vargával [12] végzett mérés pontosan igazolja a félklasszikus számításokat.
A kísérletek utóéletéről
A koincidenciakísérlet fontos elismerését L. Mandel [13] szolgáltatta utalva arra, hogy ez az egyik első bizonyítéka annak, miszerint a foton hatására fellépő elektronemisszió azonnal bekövetkezik, míg folytonos energiák esetén hosszíú idő kellene ahhoz, hogy az elektronemisszió fellépjen.
Franson és Potocki [14] megismételték az interferenciakísérletet, az eredeti munkában használt fényforrásnál jobbat használva. Most annak a valószínűsége, hogy két atom egyidejűleg bocsásson ki fényt csak egy tízezrednyi volt. Azt találták, hogy interferencia ekkor is fellép.
Jauch [15] az első két kísérletet a kvantumelmélet alapjait igazoló munkának tekintette. Ennek nyomán Clauser [16] kritikailag elemezte a két kísérletet és rámutatott azok gyenge pontjára: ha szigorúan vesszük a kvantumelméletet, akkor annyi fotonnal kell számolni, amennyit a fényforrás minden irányban emittál azon idő alatt, amíg az atomok gerjesztett állapotban vannak (ez mintegy százmilliomod másodperc). Az atomok száma igen nagy, fotonok száma is sokmillió, csak nagyon kicsi annak a valószínűsége, hogy valamely foton a berendezésben tartózkodjon. (Ugyanis a fényforrás a teljes térszögbe emittál, viszont a mérőberendezésben használt monokromátor csak nagyon kis hányadát - mintegy egy ezredét - fogja be a teljes térszögnek.) Clauser elvégzett egy a koincidenciakísérletnél bonyolultabb mérést. Olyan atomokat választott, amelyek rövid időn belül két különböző hullámhosszon sugároznak. Most csökkenthető a véletlen szerepe: az egyik hullámhosszon detektált foton jelzi a másik hullámhosszú sugárzás jelenlétét, tehát nagy valószínűséggel a másik foton is bent van a berendezésben. Ezzel a fotonnal elvégezve a koincidenciakísérletet, ő is negatív eredményt kapott az 1.b ábrához hasonló berendezéssel, tehát vagy az egyik, vagy a másik detektor jelzett fotont.
Ezzel a módszerrel az interferenciakísérlet is elvégezhető. Grangier, Roger és Aspect [17] detektálták az egyik foton létét, a másik hullámhosszú sugárzás egy, az 1.a ábra szerinti interferométerre esett. Megint csak nagy valószínűséggel volt sugárzás a berendezésben, de most az interferencia jelensége lépett fel.
Összefoglalva: Jánossy kísérletei
és az ezt követő munkák nem azt a kérdést
tisztázták, hogy a fény részecske-e
vagy hullám, hanem azt, hogy mindkettő
lehet, a kölcsönhatástól függ,
melyik természetét mutatja. Ezzel kell együttélnünk.
Irodalom
[1.] P. SELÉNYI: Ann. d. Phys. 35(1911) 444; Phys.
Rev. 56(1936) 477
[2.] G. A. CONNEL, R. J. NEMANICII, C. C. TSAI: Appl. Phys. Lett.
36(1980) 31; J. FORTNER, R.Q. YU, J. LANNIN: J. Vac. Sci.
Technol. A8 (1990) 3493
[3.] MING LAI, J. C. DIELS: Am. J. Phys. 58 (1990) 928
[4.] E. SCHRÖDINGER: Ann. d. Phys. 62 (1920) 68
[5.] L. JÁNOSSY: Acta Phys. Hung. 1 (1952) 413
[6.] L. JÁNOSSY, ZS. NÁRAY: Acta Phys. Hung.
7 (1957) 403; Nuovo Cimento Suppl. 9(1958) 588
[7.] A. ÁDÁM, L. JÁNOSSY, P. VARGA: Acta
Phys. Hung. 4 (1955) 301; Ann. d. Phys. 16 (1955)
408
[8.] R. HANBURY BROWN, R. Q. TWISS: Phil. Mag. 45(1956)
663
[9.] R. HANBURY BROWN, R. Q. TWISS: Nature 177 (1956) 27;
ibid. 178 (1956) 1744; ibid. 179 (1957) 1128
[10.] R. HANBURY BROWN: The Intensity Interferometer- Taylor
and Francis, London, 1974.
[11.] L. JANOSSY: Nuovo Cimento 6 (1957) 111
[12.] GY. FARKAS, L. JÁNOSSY, Zs. NÁRAY, P. VARGA:
Acta Phys. Hung. 18 (1965) 199
[13.] L. MANDEL: Progress in Optics, V. XIII - North Holland,
Amsterdam, 1976.
[14.] J. D. FRANSON, K. A. POTOCKI Phys. Rev. 37(1987)
2511
[15.] J. M. JAUCH: Helv. Phys. Acta 40 (1967) 559
[16.] J. F. CLAUSER: Phys. Rev. D 9(1974) 853
[17.] P. GRANGIER, G. ROGER, A. ASPECT: Europhys. Lett.
1 (1986) 173
_________________________________________
1
A nagy távolság megválasztását
az Einstein-Podolsky-Rosen-paradoxon indokolta.
2
Ma már a módszer elismert, Ausztráliában
működik egy gigantikus berendezés [10], amellyel
olyan információt nyernek a csillagokról,
amelyeket másképp nem, vagy csak közvetve tudunk
mérni.