III. SZILÁRD LEÓ NUKLEÁRIS FIZIKAVERSENY, 2000.

Sükösd Csaba
BME Nukleáris Technika Tanszék

1999-ben amerikai tudósok felhívták az amerikai kormány figyelmét arra, hogy amíg a nyugati országok köztük az Egyesült Államok - dollármilliókat költenek a kelet-európai és a szovjet utódállamokban lévő atomreaktorok biztonságának a növelésére, közben a saját nukleáris iparuk elsorvad, a meglévő nukleáris szaktudás elvész. Az utóbbi években sok amerikai egyetemen zártak be “Nuclear Engineering" tanszékeket, drasztikusan csökken az ilyen témát választó egyetemi hallgatók és doktoranduszok száma. Ez a tendencia nagyon veszélyes, hiszen a világszerte meglévő és működő atomerőműveknek nemcsak az üzemeltetéséhez, de a majdani leállításához és leszereléséhez is nagy szaktudásra van szükség. Egy atomerőmű nem hasonlítható bankhoz, vagy étteremhez, amelyeknek a bezárása - kis túlzással - egy kulcsfordulással letudható. S ha a szaktudás hamarabb vész el, akkor az atomerőművek üzeme és leállítása sem lesz biztonságos. Three Mile Island, Csernobil és Tokai Mura emlékeztetnek arra, hogy hova vezet az, ha a nukleáris létesítményeket nem az azok által megkívánt maximális gondossággal és szakmai színvonalon kezelik.

Az amerikai tudósok felhívása túlmutatott az Egyesült Államok keretein. Tavaly az OECD országokban is foglalkoztak vele, s az idén az Európai Unió keretein belül több megbeszélés is volt, amelyeken a nukleáris kultúra terjesztéséről és a nukleáris kompetencia, a nukleáris szaktudás megőrzéséről tárgyaltak.

A magyarországi közoktatásnak ezen a téren nem kell szégyenkeznie. A középiskolás fizika keretében ugyanis tanítani kellene) a magfizika és a sugárvédelem alapfogalmait. Sajnos, sok iskolában ez az anyagrész az, amelyre már nem kerül sor a közelgő érettségik és a felvételire való felkészülés miatt. Most is fülembe cseng egy kollégám panasza, aki a fiát egy nagyon jónevű budapesti gimnáziumba - ahogyan ő fogalmazott: “versenyistállóba" - íratta be, de a középiskola négy éve alatt radioaktív sugárzásról mégcsak nem is hallottak a gyerekek. Oka valószínűleg abban keresendő, hogy hosszú időn keresztül ebből a témakörből szinte egyáltalán nem szerepelt sem OKTV versenyfeladat, sem KöMaL feladat, sem pedig érettségi-felvételi feladat. A tanárok pedig a fizika iránt érdeklődő diákokat a versenyekre és a felvételire készítik fel...

Az Eötvös Loránd Fizikai Társulat - felkarolva a Tolna megyei csoport korábbi kezdeményezését - 1998-ban, Szilárd Leó születésének századik évfordulóján rendezte meg az első országos Szilárd Leó Nukleáris Fizikaversenyt. 2000-ben a harmadik országos versenyre került sor.

A versenyt a korábbiaknál is nagyobb érdeklődés kísérte. Az első (iskolai) fordulóra 442 tanulót neveztek be tanáraik. Az első fordulóban kitűzött feladatokat az iskolai fizikatanár-kollégák javították ki, és a versenyfelhívásban leírt feltételeknek megfelelt dolgozatokat beküldték az Eötvös Loránd Fizikai Társulatba, ahol azokat ismételten átnéztük, és pontszám szerint rangsoroltak.

A versenyt két kategóriában hirdettük meg, de a feladatok közösek voltak a két kategóriára. A “nagyok" kategóriájába a középiskolák 11-12. osztályosai tartoztak, a náluk fiatalabbak alkották a “junior" kategóriát. Jóllehet alsó korhatár nincs, a feladatokat elsősorban 11-12. osztályosoknak szántuk. Emiatt 9. osztályosnál fiatalabbak döntőbe kerülési esélye eléggé alacsony. A két kategóriát az különböztette meg, hogy az “utózsűrizéshez" szükséges szint a nagyoknál 60% (30 pont) volt, és 40% (20 pont) a junior kategóriában. A döntőben a nagyok és a juniorok pontszámait külön kezeltük.

Az első forduló

A verseny első (iskolai) fordulójára 2000. március 6-án 12-15 óráig került sor. A feladatok a következők voltak:

1. feladat        (5 pont)

Milyen folyamatok mehetnek végbe a ³He, ⁴He atommagoknak termikus neutronokkal történő reakciója során? Indokold is meg a választ!

Adatok. Az alábbi táblázat néhány könnyű atommag tömegét tartalmazza. A nem-stabil atommagoknál feltüntettük a felezési időt és a bomlás módját is. A tömeg-energia átalakításhoz használjuk: c² = 8,987551787 • 10¹⁶ m²/s².

Atommag	tömeg (10-27 kg)	Felezési idő	Bomlás módja
Neutron	1,6749543	1000 s
1H	1,6726485	stabil
2H	3,342727844	stabil
3H	5,005622512	12,33 év
3He	5,005589319	stabil
4He	6,64296669	stabil
5He	8,318722076	2 • 10-21 s	+n

2. feladat       (5 pont)

A környezet- és egészségvédelmi előírások szabályozzák, hogy mikor lehet radioaktív hulladékot a csatornarendszerbe kiönteni. Például ³²P izotópból csak olyan önthető ki, amelynek aktivitáskoncentrációja legfeljebb 20 MBq/m³. Mennyi ideig kell tárolni a literenként 8 • 10⁷ Bq aktivitású hulladékot a kiöntés előtt? A ³²P felezési ideje 14,3 nap.

3. feladat       (5 pont)

Biológiailag az azonos energiájú és intenzitású neutron- vagy a-sugárzás a veszélyesebb? Indokold meg a választ!

4. feladat       (5 pont)

Az 5 cm³ normál állapotú levegőt tartalmazó töltőtoll-doziméter kapacitása legyen 1 pF, és töltsük fel 1000 V-ra. Mennyi az elnyelt dózis, ha a besugárzás után a feszültsége 900 V-ra csökkent?

Adatok: A levegő átlagos ionizációs energiája 6,88 aJ, sűrűségét vegyük 1,3 kg/m³-nek.

5. feladat        (5 pont)

A Nagy Egyesítés elmélete szerint a proton sem teljesen stabil, hanem nagyon hosszú felezési idővel ⁰-mezonra és pozitronra bomlik. Egy kísérletben 3300 tonna vizet 1 évig vizsgáltak, de nem tapasztaltak egyetlen protonbomlásra utaló eseményt sem. Milyen felső határt ad ez a kísérlet a vízmolekulában lévő proton felezési idejére?

6. feladat        (5 pont)

Az 1986-os csernobili atomerőmű-baleset következtében hazánkat is érő radioaktív légköri szennyeződés során az országban a levegő aktivitás-koncentrációja átlagosan 1 Bq/m³-rel nőtt, legnagyobbrészt a 8 nap felezési idejű ¹³¹I izotóp következtében.
a) Összesen hány gramm jód érkezhetett hazánk légterébe?
b) Összesen hány gramm radioaktív jód szabadulhatott ki a csernobili sérült reaktorblokkból, ha a kiszabadult összaktivitás 10¹⁸ Bq volt? Tegyük fel, hogy ennek 90%a a jódtól származott.

Adatok: a szennyezett légkör magasságát vegyük 5 km-nek, hazánk területét pedig 10⁵ km²-nek.

7. feladat        (5 pont)

Háromszorosan ionizált UF₆ molekulákat gyorsítunk 5 kV feszültséggel, majd egy piciny nyíláson 1 T indukciójú mágneses mezőbe vezetjük őket. Az indukció vektora merőleges a sebességre.
a) Milyen pályán mozognak az ionok? Adjuk meg a 238-as, illetve a 235-ös uránizotópot tartalmazó ionpályák jellemző paramétereit.
b) Ezen a módon szét lehet választani a 235-ös és a 238-as izotópokat egymástól. A II. világháború alatt az USA-ban rendelkezésre álló ionforrások 1 mA-es ionáramot tudtak előállítani. Mennyi ideig tartott volna 1 kg teljesen tiszta 235-ös urán előállítása ezzel a módszerrel?

8. feladat        (5 pont)

Tudjuk, hogy rendszámnövelő, illetve rendszámcsökkentő -bomlások az atommagok energiavölgyének két különböző oldalán lévő atommagoknál jönnek létre. Ezért azt várnánk, hogy nincs olyan atommag, amely egyszerre lenne negatív -bomló (rendszámnövelő) és elektron­ befogó (rendszámcsökkentő). A ⁴⁰K izotóp azonban 88%-os valószínűséggel negatív -bomló, 12%-os valószínűséggel pedig elektronbefogással bomlik. (Nemcsak a ⁴⁰K ilyen, vannak még más ilyen atommagok is). Hogyan lehetséges ez?

9. feladat        (5 pont)

Egy lézer 20 J energiájú impulzust bocsát ki 0,5 ľs időtartamig 580 nm hullámhosszon. Ezt a fényt céziumlapra ejtjük 12 ľm átmérőjű körre fókuszálva. A fény kilencven százaléka elnyelődik, tíz százaléka visszaverődik.

1. Hány foton éri a fémlapot ebben az impulzusban?
2. Mekkora nyomást kelt a fénysugár?
3. Mekkora maximális sebességgel hagyják el a céziumlapot a kilépő elektronok?

Adatok: Az elektronok kilépési munkája a cézium fémből 0,3 aJ.

10. feladat        (5 pont)

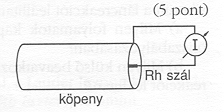
Atomerőművekben a neutronfluxus mérésének egyik módja az úgynevezett elektronemissziós (SPND) detektorokkal történő mérés. Egy ilyen detektor 3 mm átmérőjű rozsdamentes acél hengerbe helyezett, 20 cm hosszú, 1 mm átmérőjű, ¹⁰³Rh-ból készült szálból áll. A szál és a henger egymástól elektromosan el van szigetelve. A neutronsugárzás hatására a szálban -bomló ¹⁰⁴Rh keletkezik, amelyből kilépő nagy energiájú -részecskék áthatolnak a szál és a köpeny közötti szigetelésen, és elnyelődnek a köpenyben. Ezáltal a szál és köpeny közé kapcsolt árammérővel áram mérhető. (Vegyük észre, hogy ezeknek a detektoroknak az üzemeltetéséhez nem kell külön áramforrás, ezért ezeket öntápláló detektoroknak is hívják.)

1. Mekkora a Rh-szál aktivitása, ha az árammérő 0,1 ľA áramot jelez?
2. Az árammérő hosszú időn át állandó áramot mér, pedig a radioaktív anyagok aktivitásának a felezési időnek megfelelően csökkenni kellene. Hogyan lehetséges ez?
3. Az a) feladatnak megfelelő teljesítményen hány év alatt alakul(na) át a Rh-szálban eredetileg meglévő ¹⁰³Rh atommagok 5%-a?

Adatok: A ¹⁰⁴Rh felezési ideje 42,3 s. A ródium fém sűrűsége 12400 kg/m³.

Az iskolákból a 11-12. osztályosok kategóriájában 37 dolgozatot, a junior kategóriában pedig 20 dolgozatot küldtek be zsűrizésre. A beérkezett 57 dolgozatot ismét átnéztük és értékeltük. Minden feladatra érkezett jó megoldás, ami azt mutatja, hogy a feladatokat egy jól felkészült diák meg tudta oldani. A zsüri által adott pontszámok általában nem nagyon tértek el az iskolában adott pontszámoktól. Csak néhány esetben fordult elő, hogy a javító fizikatanár kolléga pontszámait erősebben meg kellett változtatni. Ezek között volt olyan eset is amikor az ELFT zsürije több pontot adott egy feladatra, mint a javító fizikatanár, aki valószínűleg nem vette észre a megoldásban rejlő újszerű, finom logikai gondolatmenetet.

A döntőbe a 11-12. osztályosok közül - a “hagyományoknak" megfelelően - a legmagasabb pontszámot elért 20 fő, a junior kategóriában pedig 10 fő jutott be. Azoknak a teljesítményét, akik nem kerültek be a döntőbe, de dolgozataik elérték a megszabott ponthatárokat, az ELFT elismerő oklevéllel jutalmazta.

A verseny döntője

A verseny döntője 2000. április 27-én volt Pakson. A versenyzők és tanáraik előző nap erőmű-látogatáson vettek részt. A döntő három részből állt: 10 elméleti feladat megoldása, két kísérleti és két számítógépes szimulációs feladat megoldása. Az elméleti feladatokért maximum 50 pontot, a két kísérleti feladatért maximum 30 pontot, a számítógépes szimulációs feladatokért pedig maximum 20 pontot lehetett szerezni.

1. feladat       (5 pont)

Milyen lenne a világ, ha a neutron tömege egy ezrelékkel kisebb lenne (a jelenlegi tömeg 0,999-szerese)? Jelenleg a neutron tömege 1,6749543 • 10^-27 kg.

Adatok: A proton tömege 1,6726486 •10^-27 kg, az elektron tömege pedig 0,9109534 • 10^-30 kg.

2. feladat        (5 pont)

A japán Tokai-Mura kémiai gyárban uránoxidot tisztítanak atomreaktor-fűtőelemek céljára. A kémiailag megtisztított uránoxidot egy tartályban vizes oldatból kémiailag kiválasztják, s az csapadék formájában a tartály aljára ülepedik. A kémiai átalakulás során fejlődött hő elvezetésére a tartályt vízburok veszi körül. A vízköpenyben hűtővíz áramlik: hidegen kintről csövön jön be, a fölmelegedett hűtővíz csövön kifolyik.

1999 őszén az történt, hogy a szokásos 3% dúsítású urán oxidja helyett (magashőmérsékletű reaktorok részére)18%-ra dúsított urán oxidját tisztították, de - a szabályokat megszegve - ugyanakkora anyagmennyiségekkel dolgoztak. Így esett, hogy a leülepedett uránoxid elérte a kritikus mennyiséget, benne hasadási láncreakció indult meg. A spontán létrejött reaktor önmagát szabályozta és 17 órán keresztül állandósulva működött. Mivel a kémiai üzemben láncreakcióra nem számítottak, a helyiségben sugárzásmérők, és szabályozó-beavatkozó automatika nem volt. A váratlanul kialakult magas neutronszint miatt nem is lehetett belépni a helyiségbe. 17 óra után külső beavatkozással sikerült a láncreakciót leállítani.

1. Milyen folyamatok kaphattak szerepet a hasadási láncreakció önszabályozásában?
2. Milyen külső beavatkozás volt képes a zárt tartályban folyó láncreakciót leállítani?

3. feladat        (5 pont)

A Napban (több lépésen át) ¹H ⁴He magfúzió termeli az energiát, ami a napfényt táplálja.

1. Milyen lett volna a Nap sorsa, ha a ²He atommag stabilan létezne?
2. Milyen lett volna a Nap sorsa, ha a ²H izotóp nem létezne?

4. feladat        (5 pont)

Környezetvédelmi-környezettisztasági szempontból hasonlítsd össze az (azonos teljesítményű) szénerőművet, gázerőművet, atomerőművet!

5. feladat        (5 pont)

A csernobili baleset után Lengyelországban megmérték a lehullott radioaktív szennyezésben a ¹³⁴Cs/¹³⁷Cs arányt (a két izotóp különböző energiájú -sugárzást bocsát ki, s így meg lehet őket különböztetni). A mérések eredményéből meg lehetett állapítani, hogy a fűtőelemek már hosszú ideje a reaktorban voltak.

1. Miért lehet ebből arra következtetni, hogy a reaktor nem atomfegyver-alapanyagot termelt?
2. Nem sokkal később Észak-Olaszországban egy gombafajtában is megmérték a ¹³⁴Cs/¹³⁷Cs arányt, s azt találták, hogy a gomba csaknem kizárólag ¹³⁷Cs-ot tartalmazott. Azt jelenti-e ez, hogy a gomba különbséget tud tenni ugyanazon elem különböző izotópjai között?

Adatok: A ¹³⁴Cs felezési ideje 2 év, a ¹³⁷Cs felezési ideje 30 év.

6. feladat        (5 pont)

A vörös óriás csillagokban ⁴He-ból fúzióval épülnek fel a magasabb rendszámú elemek. Ennek a fúziós folyamatláncnak nehéz az indulása, mert a ⁴He+⁴He ⁸Be atommag-reakció végterméke nem stabil, hanem szinte rögtön szétesik. Fred Hoyle feltételezte, hogy elegendően nagy sűrűség esetén az is előfordulhat, hogy a ⁸Be igen rövid élettartama alatt egy harmadik ⁴He atommaggal találkozik, s akkor a ⁸Be+⁴He ¹²C folyamatban ¹²C atommag keletkezhet. Miután ehhez 3 db -részecske igen rövid időn belül való találkozására van szükség, ezt a folyamatot 3 folyamatnak nevezik. Hoyle számításai szerint azonban ennek is csak akkor lehet számottevő szerepe, ha a ¹²C atommagban van olyan gerjesztett állapot, amely a 3 db -részecskéből könnyen létrejöhet, s amely azután -foton kibocsátásával alapállapota bomlik. Hoyle jóslatát követve Fowler, a California Institute of Technology munkatársa hamarosan kísérletileg is megtalálta ezt a gerjesztett állapotot a ¹²C atommagban.

Vajon mekkora gerjesztési energia közelében kellett Fowlernek ezt az állapotot keresnie a ¹²C atommagban?

Adatok: A ⁴He atommag tömege 6,64296669 • 10^-27 kg, a ¹²C atommag tömege pedig: 19,91593977 • 10^-27 kg, s tegyük fel, hogy az -részecskéknek 4 fm-re meg kell közelíteniök egymást, hogy az összeolvadás létrejöhessen.

7. feladat        (5 pont)

Bizonyítsuk be, hogy egy ²H + ²H ³He+n fúzióval működő állandó hőmérsékletű plazmában a fúziós teljesítménysűrűség a plazma sűrűségének négyzetével arányos.

8. feladat       (5 pont)

Egy plutónium-tárolóban azonos méretű, plutóniumból készült fémgömbök vannak egymástól biztonságos távolságra elzárva. Egyes gömbök tiszta ²³⁹Pu-ból készültek, mások pedig tiszta ²⁴⁰Pu-ból. Sajnos, az azonosító felirat elmosódott rajtuk. Adj módszereket a szétválogatásukra.

Adatok: A ²³⁹Pu felezési ideje 24100 év, a ²⁴⁰Pu felezési ideje pedig 6560 év.

9. feladat        (5 pont)

Képzeld el, hogy a Szabadalmi Hivatalban dolgozol. Szabadalmi beadvány érkezik, amely azt javasolja, hogy az urán dúsítására eddig használt urán-hexafluorid (UF₆) gáz helyett urán-hexakloridot (UCl₆) használjanak. Azzal érvel, hogy ez a vegyület sokkal kevésbé mérgező és korrozív, mint az UF₆, s ezért a dúsítóberendezések sokkal olcsóbb anyagokból is felépíthetők lennének. Az UCl₆ kémiai tulajdonságait nem ismered. Tudsz-e mégis véleményt mondani erről a javaslatról?

10. feladat        (5 pont)

Hogyan alakult volna a világ sorsa, ha az ²³⁵U felezési ideje 2,25 milliárd év lenne?

11. kísérleti feladat

Vizsgáld meg a kiadott ásványi por radioaktivitását! Milyen típusú sugárzásokat lehet detektálni? Határozd meg ezek mérhető intenzitásainak arányait! Erre a feladatra összesen 80 perc áll rendelkezésre. A pormintára tett fóliát nem szabad eltávolítani.

12. kísérleti feladat

Határozd meg minél pontosabban a kiadott fecskendőből kivonható - oldatban lévő - radioaktív anyag felezési idejét (perc nagyságrendű). Erre a feladatra 40 perc áll rendelkezésre, utána a fecskendőt tovább kell adnod egy másik versenyzőnek.

Mérőkészülék: A mérésekhez rendelkezésre áll egy végablakos GM-csöves sugárzásmérő készülék. A készülék használható önállóan is, vagy számítógéphez csatlakoztatva.

Önálló esetben a mérést a Start/Törlés-Stop gombbal lehet elindítani (ez a mérés megkezdése előtt automatikusan törli is a számláló állását), és a gomb másodszori megnyomására a mérés megáll. A készülék önálló időzítéssel nem rendelkezik.

Számítógéphez csatlakoztatás esetén a C:\Szilard könyvtárban lévő Start.bat fájlt kell elindítani, és a bejelentkező képernyő (Qbasic) után a mérőprogram a Shift/F5 megnyomására indul. Ekkor a számítógépen megadható a mérési időintervallum másodpercben. A képernyőre a mérési idő letelte után a gép kiírja az időt és a mért beütésszámot, és a mérést azonnal újraindítja. Az ESC lenyomásával visszatérhetsz a mérési idő megadásához. A program megáll, ha 0 s mérési időt adsz meg. (Ezek a programok csak DOS környezetben futnak.)

Az oldat elkészítése: A fehér színű anyagot tartalmazó fecskendőt állítsd be a kiadott kis hosszúkás műanyag edénybe, s a másik fecskendő segítségével tölts rá körülbelül 1 ml oldatot. Az átcsurgott folyadékkal megkezdheted a mérést. Takarékoskodj az oldattal, ugyanazt az oldatot a lebomlás után ismét felhasználhatod! Az elhasznált oldatot a teremben lévő gyűjtőedénybe öntsd.

(A verseny után megmondtuk, hogy a kiadott “ásványi por" uránércőrlemény volt. A feladatban szereplő oldatot egy ¹³⁷Cs-¹³⁷Ba “izotópgenerátorból" kellett a versenyzőknek elkészíteni. A versenyzők figyelmét szóban is felhívtuk arra, hogy radioaktív anyaggal dolgoznak, és különös óvatossággal tevékenykedjenek: Az izotópgenerátorokban pedig olyan kis aktivitású ¹³⁷Cs izotóp volt, amely az ÉFEK (éves felvételi korlát) tizedrészét sem érte el, azaz még a teljes mennyiség véletlen lenyelésekor sem lett volna komolyabb következménye. (A véletlen lenyelés már csak azért sem történhetett meg, mert a ¹³⁷Cs izotóp egy kis fecskendőben lévő szilárd anyagban volt megkötve.) Az izotópgenerátorok elkészítésért a BME Nukleáris Technika Tanszéken Vajda Nóra docensasszonynak mondok köszönetet.)

A versenyzők a következő szövegű feladatlapot kapták: Ez a program alapvetően a nukleáris láncreakció nagyon leegyszerűsített formában történő modellezésére szolgál.

Néhány előre megadott háromszög alakú elemből, mint különböző dúsítású (természetes, 5%-os, illetve 100%-os) uránrúdból, különböző (könnyűvíz, nehézvíz, grafit) moderátorból, szabályozó rudakból és neutronforrásból lehet összeállítani különböző elrendezéseket, majd vizsgálni, hogy kialakul-e a szabályozott nukleáris láncreakció, illetve miként lehet azt szabályozottá tenni. Az urándúsítást és a moderátort a Beállítások menüpontban lehet megadni.

A program működése: Az egyes cellákban lévő neutronok két csoportba sorolhatók: gyors, illetve lassú neutronok. Ezeknek a számát a cellákba különböző színekkel írt számok mutatják. Az idő múlását “órajelek" modellezik. Minden órajelre a cellákban lévő neutronokkal a következő dolgok történhetnek (különböző valószínűségekkel):
- Keletkezés (gyors neutronként, urán rudakban, illetve neutronforrásban),
- elnyelődés (kivéve az “üres" cellákat),
- hasítás (csak urán rudakban),
- lelassulás (csak a gyors neutronok),
- átlépés a szomszéd cellába.

Az alsó sorban megjelenő “sokszorozási tényezőt" a program a következő módon számolja: a nem-üres cellákban lévő neutronok számát elosztja az előző generációban ugyanezen cellákban meglévő neutronok számával. (Mivel a neutronok száma statisztikusan ingadozik, ezért az így kiszámolt sokszorozási tényező is ingadozik.)

Feladatok:

1. Állítson elő természetes urán felhasználásával minél kevesebb elemből olyan elrendezést, amely éppen kritikus! Hány urán rudat (uránháromszöget) kellett felhasználni?

2. Vizsgálja meg, hogy legalább hány darab 5%-osan dúsított uránrúd szükséges egy kritikus rendszer összeállításához víz, nehézvíz, illetve grafit moderátor felhasználásával!

3. Miért célszerű a hőmérsékleti visszacsatolást kikapcsolni, amikor a kritikus tömeget keresi?

A feladatok megoldását részletesen írja le. Írja fel a szükséges adatokat, készíthet grafikonokat, rajzokat az elrendezésről stb.

Néhány tanács:

• Az önfenntartó nukleáris láncreakció beindításához minden eseten szükség van neutronforrásra. Ezért a különböző elrendezések során helyezzen el neutronforrást is, és néhány generáción keresztül ezzel működtesse, majd cserélje ki másik elemre!
• A kritikus tömeg megállapításához célszerű a hőmérsékleti visszacsatolást kikapcsolni a Beállítás/Hőmérséklet menüvel. (ld. 3. feladat)
• A program lehetőséget ad arra, hogy egy adott elrendezést, “működés" közben módosítson. (Szünet/Pause gomb, majd módosítás után a szimuláció folytatható).
• A grafikonok egyes részletei a Shift gomb lenyomása mellett az egérrel kijelölhetők és nagyíthatók. Az eredeti méretre való visszaállítás a Shift gomb lenyomása mellett az egérrel a grafikonra kattintással történik.

A szimulátor egy tipikus képernyőábrája a következő. A piros háromszögek uránrudat, a kék háromszögek moderátort, a zöld háromszögek pedig “üres" elemeket jelölnek. A zöld számok az egyes cellákban lévő gyorsneutronok számát, a fehérek pedig a lassú neutronok számát jelzik. A képernyő jobb oldalán az építéshez és a futtatáshoz szükséges kezelőgombok találhatóak.

A III. Szilárd Leó Fizikaverseny eredményei

A döntő után ismertettem a feladatok helyes megoldását a versenyzőkkel és kísérőtanáraikkal. Elmondtam, hogy míg az első fordulóban nagyobb hangsúlyt kaptak a “hagyományosnak" tekinthető számításigényes feladatok, a döntő feladataival inkább a versenyzők nukleáris kultúráját, látókörének szélességét igyekeztünk tesztelni. Itt is minden elméleti feladatra érkezett csaknem 100%-os megoldás is, jóllehet összesítve egyetlen tanuló sem ért el még 75%-os eredményt sem. Meglepő (?) tapasztalat volt, hogy még a legjobb tanulók kísérletezési kultúrája sem kielégítő. Ezt tükrözték mind a kísérleti feladatokra, mind pedig a számítógépes szimulációs feladatokra kapott alacsony pontszámok. (Hiszen a számítógépes szimuláció is bizonyos értelemben kísérletezés volt.) Ennek jelzésértéke van: arra utal, hogy a fizikaóra keretében lassan elhal a tanulói kísérletezés. Még a fizika iránt érdeklődő diákok sem tudják megszerezni azokat az alapvető módszertani ismereteket, amelyek nélkül nem lehet sikeres kísérleti munkát végezni. Ez az ismertető cikk nem alkalmas arra, hogy erre az igen összetett és sok - tanártól részben független tényezőtől is függő - kérdésre itt részletesebben kitérjek, de mindenképpen fel szeretném hívni a figyelmet arra, hogy itt egy nem kívánatos tendencia egyértelmű megnyilvánulását látjuk.

Itt csak a legjobb versenyzők neveit, osztályát, össz-pontszámait, valamint iskolájuk és tanáraik nevét sorolom fel külön a 11-12. osztályosok, és külön a junior kategóriában.

11-12. osztályosok

1. díjat kapott CZIGLER ISTVÁN (74 ponttal, a Lauder Javne iskola, Budapest 12. osztályos tanulója, tanára: Tóth Eszter) valamint
PATAY GERGELY (74, Tóth Árpád Gimnázium, Debrecen, 12., Kovács Miklós)

3. díjat kapott BALOGH. ZOLTÁN (71, Bolyai János Gimnázium, Salgótarján, 12., Deák Norbert)

4. díjat kapott JUNG JÁNOS (66, Petőfi S. Evang. Gimnázium, Bonyhád, 12., Erdélyesi János)

5. díjat kapott BOGATIN GYÖRGY (64, Zrínyi Miklós Gimnázium, Zalaegerszeg, 11., Vadvári Tibor)

Junior kategória

1. díjat kapott FARKAS ÁGNES (72, SZTE Ságvári E. Gyak. Gimnázium, Szeged, 10., Kovács László)

2. díjat kapott DOMOKOS GÁBOR (58, Bolyai János Gimnázium, Kecskemét, 9., Svihrán Éva)

3. díjat kapott GERESDI ATTILA (56, Árpád Fejedelem Gimnázium, Pécs, 10., Győrpál Elemérné)

4. díjat kapott ÁBEL DÁNIEL (52, Németh L. Gimnázium, Budapest, 10., Zsigri Ferenc)

5. díjat kapott NAGY ÁGNES (48, SZTE Ságvári E. Gyak. Gimnázium, Szeged, 10., Kovács László)

A zsűri az azonos pontszámot elért tanulókat azonos díjban részesítette. Ezért van a 11-12. osztályosok kategóriájában két első díj, viszont nincs második díj. A nyerteseknek ezúton is gratulálunk.

Tanári különdíj

Az Országos Szilárd Leó Fizikaverseny versenybizottsága - a Szilárd Leó Alapítvány kuratóriumával egyetértésben - “Tanári különdíjat" alapított. Ezt a díjat minden évben az Országos Szilárd Leó Fizikaversenyhez kapcsolódva ítélik oda egy fizikatanárnak, akinek a nukleáris kultúra terjesztése érdekében végzett munkáját és eredményeit a zsűri kiemelkedőnek tartja. Ebben az évben ezt a díjat PÁLOVICS. RÓBERT tanár úr, a zalaegerszegi Zrínyi Miklós Gimnázium tanára vehette át. A kitüntető oklevél szövege: “Oklevél Pálovics Róbert tanár úr részére, akit a 2000. évi Országos Szilárd Leó Fizikaverseny versenybizottsága a nukleáris kultúra terjesztése érdekében kifejtett folyamatos és eredményes tanári munkájáért tanári különdíjban részesít." Köszönjük munkáját.

A szervezésért külön köszönet illeti Csajági Sándor tanár urat, a Paksi Energetikai Szakképzési Intézet tanárát. Köszönetet mondok a Paksi Atomerőmű Rt.-nek azért, hogy a verseny megszemezését anyagilag is támogatta, az Energetikai Szakképzési Intézet vezetőjének azért, hogy a döntő lebonyolításához a helyszínt adta és a lebonyolítás zavartalanságát biztosította, s nem utolsósorban az ELFT Titkárságának, hogy a verseny adminisztrációjával kapcsolatos többletmunkát kiváló színvonalon elvégezte.

Felhívjuk a fizikatanár-kollégák figyelmét, hogy 2001-ben is lesz Országos Szilárd Leó Nukleáris Fizikaverseny. Biztatni szeretném őket, hogy készítsék fel tanulóikat, s minél több versenyzőt nevezzenek majd erre a megmérettetésre.