Fizikai Szemle honlap |
Tartalomjegyzék |
Fizikai Szemle 2001/3. 80.o.
Schuszter Miklós, Bodnár Zoltán, Mojzes Imre
BMGE Elektronikai Technológiai Tanszék
Dobos László
MTA-MFA
1. Bevezetés
A ma használatos mikroelektronikai alkatrészek nagy többségének anyaga a szilícium. Egyedülálló tulajdonságai, szinte korlátlan mennyisége, kiforrott technológiája lehetővé teszi, hogy igen sokféle áramköri funkciót valósítsunk meg alkalmazásával. Ezzel együtt vannak olyan területek, ahol a szilícium tulajdonságai nem megfelelőek. Ezeken a területeken alkalmazzák sikerrel a vegyület-félvezetőket, amelyek lényegüket tekintve mesterséges anyagok, hiszen nagy többségük a természetben ásványként nem fordul elő. Ezek az anyagok szolgálnak alapanyagul egy sor mikrohullámú és optoelektronikai elem elkészítéséhez. Ezekben a félvezető eszközökben a vegyület-félvezetők olyan tulajdonságait használják ki, mint a direkt sávszerkezet, a nagy töltéshordozó-mozgékonyság, a széles tiltott sáv, a magas működési hőmérséklet és az alacsony zajszint. E tulajdonságokat – bizonyos határok között – az anyagösszetétel változtatásával befolyásolni lehet. A vegyület-félvezetők közül legfontosabb szerepet a gallium-arzenid (GaAs) és az indium-foszfid (InP) játssza. Ezekből az anyagokból, illetve ezek alapján készített, módosított összetételű epitaxiális rétegekből, készülnek többek között a műholdvevőben használt tranzisztorok, a CD lejátszó és a lézeres mutatópálca vörös fényű lézere, valamint az optikai hírközlésben használt infravörös lézerek is.
A vegyület-félvezetők technológiája mintegy 5-8 éves lemaradással követi a szilícium technológiát. Ez a szeletméretre, és az alkatrészsűrűségre egyaránt vonatkozik. E lemaradás egyik oka, hogy a vegyület-félvezetők technológiája lényegesen bonyolultabb, mivel anyaguk kevésbé stabil, kémiai tulajdonságaik kevésbé kedvezőek. A legnagyobb fékezőerőt azonban az jelenti, hogy oxidjaik általában nem alkalmasak a szilícium technológiában szokásos MOS-típusú struktúrák előállítására, valamint az, hogy felületükön mind a Schottky, mind az ohmos kontaktusok kialakítása lényegesen bonyolultabb, mint az a szilícium technikában megszokott. Vizsgálataink az utóbbi problémára, a kontaktusok kialakítására vonatkoznak.
A kontaktus kialakítása során a felpárologtatott fém alapú vékonyréteg rendszer általában nem eredményez ohmos kontaktust, hanem Schottky típusú, tehát egyenirányító tulajdonságokat mutat. Ha a célunk kis fajlagos ellenállású, ohmos kontaktus kialakítása – mint például egy félvezető lézerdióda esetében –, akkor ehhez a fémréteg felgőzölésén túl egy további műveletre, a hőkezelésre van szükség, tehát a vegyület-félvezető eszközök technológiájának fontos része a hőkezelés. A kontaktusok mechanikai tulajdonságai (kiköthetőség, tapadás a hordozóhoz) is változnak a hőkezelés során az anyagszerkezetükben létrejövő maradandó fázisátalakulásoknak köszönhetően, és más elektromos jellemzőik is befolyásolhatók a hőkezelés során (mint például a kontaktusellenállás, vagy a hőmérsékleti stabilitás). A hőkezelési folyamatot a hőprofil jellemzi, amely a hőkezelés időtartamáról és a hőmérséklet időbeli változásáról nyújt információt.
Széles körben folynak kutatások a vegyület-félvezetőkhöz készített kontaktusok anyaga megválasztásának és az egyes kontaktusfémezések számára megfelelő hőprofil kialakításának irányában. Gallium-arzenidhez kontaktusként hagyományosan arany-alapú fémezéseket alkalmaztak. Ezek a fémezések nem kizárólag aranyat, hanem más összetevő(ke)t is tartalmaztak, mivel a csupán aranyat tartalmazó fémezések esetében az arany már viszonylag alacsony hőmérsékleten (350 ° C felett) reakcióba lép a gallium-arzeniddel, illetve bediffundál a gallium-arzenidbe [1,2,3,4], sőt hosszabb időtartam (néhány hónap) alatt szobahőmérsékleten az arany – gallium-arzenid határfelület mentén arany-gallium vegyület jön létre [5,6,7].
Az arany káros hatásainak kiküszöbölésére újfajta fémezésekkel kísérleteznek. Az egyik irányzat szerint az aranyat egy másik anyaggal (pl. alumínium) váltják fel, míg egy másik szerint az arany kikötési réteg és a gallium-arzenid hordozó között megfelelő elválasztó (barrier) rétege(ke)t alkalmaznak az arany – gallium-arzenid kölcsönhatást megakadályozandó.
A cikkünkben bemutatott vizsgálatunk során a palládiumot, mint fémezési anyagot vizsgáltuk. A palládium önmagában nem alkalmas kontaktálási célokra, mert kiköthetősége nem megfelelő, ezért arany kikötési réteggel kell bevonni [2,3,8,9,10]. A fenti megfontolások vezettek minket az Au/Pd kétrétegű fémezés tulajdonságainak vizsgálatához.
A fraktálelmélet a természeti jelenségek és a természetben lezajló, illetve mesterségesen létrehozott folyamatok leírására alkalmazott újszerű modellek alapjául szolgál. Sokféle tudományterületen alkalmazzák már, olyan esetekben, ahol a jelenség vagy folyamat a hagyományos módszerekkel nem, vagy csak igen nehézkesen volna leírható. A mikroelektronika területén is ismeretesek kutatások a fraktálviselkedésű rendszerek irányában, de a vegyület-félvezetőkön végzett kutatások során – tudomásunk szerint – egyedülálló a fraktálelméleti modellt alkalmazó megközelítés.
Fraktálmatematikai analízisünk során a kontaktusok felszínéről a hőkezelés közben készített ’in situ’ SEM fényképfelvételek jelentették a kiindulási alapot. Ezeket a felvételeket egy átalakított SEM készülékben készítettük, ahol megoldottuk a gyors, max 700 ° C-os hőmérsékletű hőkezelést. A felvételek kiértékeléséhez a modern technika lehetőségeit kihasználva számítógépes eljárást dolgoztunk ki. A SEM fényképeket digitalizálva számítógépes bitmap (BMP) képeket hoztunk létre, amelyek alkalmasak voltak szoftveres kiértékelésre. A bizonyos hőmérséklettartományokon készült képeket szemrevételezve azokon egyértelműen egy, kettő, három, esetleg több, jellegzetes intenzitással bíró fázis (klaszter) különült el. Természetesen egy fázis esetében homogén mintázatról beszélhetünk, amelyet klasszikus értelemben nem tekinthetünk fraktálnak, ellenben több fázis esetén a mintázatot fraktáljellegűnek feltételezve végeztük a kiértékelést. A kiértékelési eljárás egyik legnagyobb nehézsége annak eldöntése, hogy milyen jellemző intenzitásérték-határok között tartozik az adott képpont az egyik vagy a másik klaszterhez. Abból a célból, hogy minél pontosabban és minél kevésbe szubjektív módon legyenek az egyes klaszterek elkülöníthetők – s ezáltal a vizsgált mintázat fraktáljellemzői megállapíthatóak –, több matematikai/számítógépes eljárást is kidolgoztunk.
A jelen cikkünkben közreadott eredményeknek van még egy sajátossága. Mi ugyanis egy vékonyréteg rendszer és a vegyület-félvezető közötti termikus kölcsönhatás eredményét vizsgáljuk. A felületen e kölcsönhatás eredményeképpen kialakuló mintázat tehát anyagtudományi folyamatokat jellemez. Vizsgálataink során igyekeztünk a kölcsönhatás körülményei (időtartam, hőmérséklet), a folyamatban résztvevő anyagok és a hordozó tulajdonságai között összefüggést találni. A fraktál technika itt tehát nem cél, hanem eszköz egy anyagtudományi folyamat leírására. Vizsgálataink azt is megmutatták, hogy önmagában ez a technika ugyan érdekes új információkat ad a fraktál mintázatot eredményező anyagtudományi kölcsönhatásról, a kölcsönhatás lényegi folyamatairól, de a folyamat teljes megértése csak további in situ és ex situ analitikai módszerek alkalmazásával érhető el. Az adott kísérleti elrendezésben mi a kölcsönhatás eredményeképpen kipárolgó illékony komponens (arzén a GaAs és foszfor az InP hőkezelésekor) hőfokfüggését vizsgáltuk. s ebből vontunk le szignifikáns következtetést a hőkezelés során kialakuló kontaktus elektromos paramétereire.
2. Kutatásaink során alkalmazott fraktálmatematematikai módszerek
A kutatásaink egyik legfontosabb része a vegyület-félvezető–fém kontaktusok felületén kialakult morfológia változásait ábrázoló elektronmikroszkópos képek analízise volt. Ezen mintázatok vizsgálatakor munkánk két legfontosabb iránya a digitalizálás kérdése és a matematikai módszerek kiválasztása volt. Mivel a képeken látható mintázatok szemmel láthatóan bonyolult, statisztikai értelemben önhasonló alakzatok, ezért a fraktálmatematika eszközeit vettük alapul, s ezek segítségével vizsgáltuk a mintázatok fraktáldimenzióját és multifraktál-spektrumát. A módszerek kiválasztásánál figyelembe vettük a mérnöki precizitással járó elvárásokat is, és teszteltük számítógépes eljárásainkat olyan esetekre, melyeknél elméleti számításokkal is megkaphattuk a dimenziót.
A nagyteljesítményű számítógépek megjelenésének köszönhetően az egyik legdinamikusabban fejlődő tudományágazat a fraktálgeometria. Matematikai értelemben olyan geometriai alakzatokat nevezünk fraktáloknak, melyeknek dimenziója nem egész szám. Kutatási ciklusunk elején leginkább korrelációs eljárással az úgynevezett globális dimenziót számoltuk ki a mintázat uniformitásával (mindenütt egyformaság) kapcsolatos számítások nélkül. Ennek az eljárásnak a lényege annak vizsgálata, hogy a minta felületi rajzolata hány nagyságrenden keresztül önhasonló, és milyen dimenziót mutat. A boxdimenzió definíciójával kapcsolatos gondolatmenetre épülő algoritmussal (box counting) nem lehetett volna a több nagyságrendig tartó önhasonlóságot megvizsgálni. Módszerünk nem a korrelációs függvény, hanem annak integráljára vonatkozó számításokra épül. Számítógépes algoritmussal kezdetben a következő eljárást valósítottuk meg:
A fekete-fehér bittérkép (BMP) fájlokban tárolt képeken a fekete mintázatot tekintettük érdekesnek a fehér háttéren. Véletlenszerűen kiválasztottunk ezer fekete pontot, majd e pontok körül a kétszer kettes boxoktól a százszor százas boxokig bezárólag integráltunk, azaz egyszerűen összegeztük a boxokban lévő fekete pontok számát. A boxokban lévő fekete pontok számát a box tömegének elnevezve átlagoltuk az azonos méretű boxok tömegét, és ennek skálázási törvényét log-log ábrán egyenes-illesztéssel és a statisztikából ismert korrelációs együtthatóval vizsgáltuk. Ahol az egyenes-illesztés hibája kicsi volt (0,02-0,03), és a korrelációs együttható értéke közel 1 volt, ott megállapítottuk a két nagyságrenden keresztül tartó statisztikai önhasonlóságot, és az egyenes meredekségét neveztük dimenziónak. Ezzel az eljárással olyan új paramétert (számot) kaptunk, melyet összevethettünk kísérleteink során kapott más paraméterekkel; így a kép exponálása pillanatában mért hőmérséklettel, és az arzén (vagy foszfor) kipárolgási értékkel.
Ezt a matematikai eljárást több determinisztikus fraktálon – melyeket iterációval hoztunk létre és BMP fájlként tároltunk – kipróbáltuk, és meglepően jó egyezést kaptunk az elméleti értékekkel. Például a Sierpinski háromszög dinamikájának tizedik iteráltjára 1,61
![]() 0,03 –at kaptunk, míg az elméleti érték 1,58.
0,03 –at kaptunk, míg az elméleti érték 1,58.
2.1. A digitalizálás témaköre
Módszerünk alkalmazásakor azonban felvetődött az elektronmikroszkópos képeken látható hibák korrigálásának kérdése, mivel képeink általában nem mutatták tökéletesen a kialakult mintázatot. Ezt három fő okra vezettük vissza:
Kezdetben nehezen birkóztunk meg ezzel a problémával. Gondolatunk az volt, hogy az elektronmikroszkópos képet 256 különböző szürkeségi értékű (árnyalatú) BMP fájlként tárolva, mint egy kétváltozós függvényt egy bizonyos értéknél – vágási szint – elvágva e szint felett feketének alatta fehérnek (vagy éppen fordítva) választottuk a kép egy adott pixelének (képpontjának) színértékét. Ekkor azonban a dimenzió függött a vágási értéktől, melyet vizuális módon választottunk ki összehasonlítva az eredeti mintázatot az így készült digitalizált képpel. A számításaink során olyan függvényt kaptunk a vágási érték–dimenzió grafikonra, mely a fehér képektől a fekete felé haladva monoton növekedő volt, a teljesen fekete képekre kettőt adott, míg a fehér irányban az egyenes-illesztés inkonzisztenssé vált. A monoton növekedő vágási érték–dimenzió grafikon jól összefügg a dimenzió entrópia jellegével.
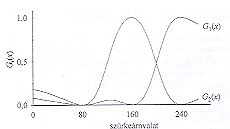
1. ábra. Függvényünk menete i=2-re és i=3-ra, n=3, m=2, v1=80, v2=160 és v3=240 esetére
A későbbiek során inkább a képre jellemző pixelérték–pixelszám görbe alapos tanulmányozásával választottuk ki a vágási értéket. Ennek a grafikonnak vízszintes tengelyén 0-tól 255-ig a különböző szürkeségi értékeket vettük, és hozzárendeltük a képen az ilyen színű pixelek számát (hisztogram). Így ideális esetben két, esetleg három jól elkülöníthető mintát (klasztert) fedeztünk fel, és ez alapján döntöttünk a vágási értékről (pl. két klaszteres esetben a két mintához tartozó maximumérték számtani közepének választva a vágási értéket). Amikor a spektrum nem ad egyértelmű megoldást, a két módszert együtt alkalmaztuk, úgy hogy a képre egérrel rákattintva szereztünk információt az érdekes mintázatról és a háttérről (oly módon, hogy a szoftver visszaadja a kiválasztott pixel intenzitás-értékét), és ezt az értékpárt is figyelembe vettük a spektrum analízisénél.
2.2. A puha szegmentáció
Egy új gondolatsor, melynek lényege, hogy a képről kapott információt nem vágással kapjuk meg, tehát nem digitalizáljuk a képet fekete és fehér részekké, hanem egy “Grade of Membership” (nem fordítottuk – továbbiakban GM) függvény segítségével szegmentálunk [11]. Ez a függvény 1 értéket vesz fel, ha a mintázathoz tartozó pixel szürkeségi értéke közelében vagyunk, és 0-t, ha a háttér vagy hátterek szürkeségi értékének megfelelő értékhez rendeljük hozzá. A GM függvény képlete:
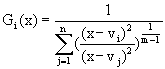
ahol i az i-edik mintázat indexe, vi az i-edik mintázatnak megfelelő színérték, esetünkben a szürkeségi érték, x pedig a vizsgált a pixel szürkeárnyalata. Nyilván ezt a függvényt 256 színű szürkeskálás BMP fájloknál csak 0 és 255 közötti egész számokra kell figyelni, s ez jelentősen leegyszerűsíti az eljárásokat. A függvény a végtelenben 1/n értékhez közelít. (kétklaszteres esetben 0,5-höz, így jelezve, hogy a végtelen mindkét mintázattól egyforma távolságra van). A két szomszédos mintázatnak megfelelő szürkeségi érték számtani közepénél 1/2 a függvény értéke, ami elvárható ebben az esetben. A képletben n jelenti az analizált képen elkülöníthető mintázatok (klaszterek) számát, m pedig a súlyozási exponens; m=2 értékre egy “sima” lefutású függvényhez jutunk, melynek kapcsolata van az interpolációs polinomok elméletével. Nagyobb m értékeknél “szigorodik” a függvény és csak a mintázathoz közel eső értékekhez rendel 1-et, míg minden máshoz 0,5 értéket ad (kivéve a hátteret) n=2 esetén. Három összetevőjű mintázat esetén a GM függvény menete adott vi értékekre a 1. ábrán látható:
A GM függvénynek szemléletes jelentése az, hogy megmondja, mennyire tartozik a minta a klaszterhez és mennyire a háttérhez. Mivel az összes mintázathoz rendelt GM értékének összege 1, ezért egyfajta valószínűségként is felfogható.

2.3. Fraktálmatematikai analízis puha szegmentációval
Eddigi fraktálmatematikai módszereink átprogramozása a puha szegmentáció esetére több problémát is felvetett. Gondolatmenetünk szerint egy BMP-néző szoftver alkalmazásával egérrákattintással és/vagy pixelszám-pixelérték spektrum (hisztogram) segítségével kapjuk meg a mintázatok szürkeségi értékét. Ezek után egyszerűen a minta
 sűrűségének a GM függvényt választjuk, azaz a minta sűrűsége az adott pontban megegyezik a pixel szürkeségi értékének GM értékével.
sűrűségének a GM függvényt választjuk, azaz a minta sűrűsége az adott pontban megegyezik a pixel szürkeségi értékének GM értékével.
![]()
A ![]() függvény szemléltetése egy kiindulási SEM felvételről készített bitmap képen alkalmazva a
2. ábrán látható.
függvény szemléltetése egy kiindulási SEM felvételről készített bitmap képen alkalmazva a
2. ábrán látható.

2. ábra ![]() függvény szemléltetése a) az eredeti kép b) a sötétebb árnyalatú klaszter
függvény szemléltetése a) az eredeti kép b) a sötétebb árnyalatú klaszter
![]() sűrűsége vizuálisan megjelenítve
sűrűsége vizuálisan megjelenítve
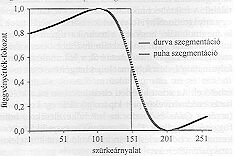
A korábbi vágásos módszerünknél a sűrűség értéke 1 volt a mintázaton, és 0 a háttéren, vagyis egyfajta lépcsős függvényként foghatjuk fel a vágásnál vett GM függvényt. Ezért ezt durva szegmentációnak, míg a fentebb említettet puha szegmentációnak nevezhetjük 3. ábra. A durva és a puha szegmentáció összehasonlítása
(3. ábra).
Az elmélet tehát látszólag könnyen átilleszthető a gyakorlatba, azonban a módszer kidolgozása számos kérdés miatt mégiscsak komplikált. A korrelációs analízis esetén ugyanis ebben az esetben nehéz eldönteni, hogy honnan kezdjük a boxnövesztést, hiszen korábban csak a fekete pixelek esetén tettük ezt, vagyis ahol a sűrűség értéke egy volt. Puha szegmentáció esetén azonban a pontosan egy értékű pixelek száma kevés, hiszen ha egy pixel szürkeségi értéke csak kicsit is eltér a mintázattól, a sűrűség értéke az adott helyen már kisebb, mint egy. Felvetődött, hogy minden pixelt “megengedünk” és a korreláció definíciója értelmében a súlyozott átlagát vesszük a boxtömegeknek, melyeket ezúttal a boxokban lévő pixelek sűrűségértéke adja. Ez az algoritmus a következő levezetésen alapul:
A korrelációs függvény definíciója:
![]()
A korrelációs függvény hatványalakja egyben a mintázat önhasonlóságát jelenti. Ha ezt a függvényt kiintegráljuk, szintén hatványalakot kapunk, ahol a kitevő a dimenzió. Ekkor a következő összefüggés áll fenn:
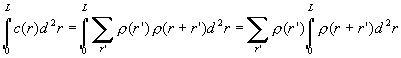
A képletből látható, hogy ha a sűrűség kicsi az r’ pontban, akkor az r’ középpontú L sugarú gömb (négyzet) elhanyagolható értékkel járul hozzá a szummához, melyet a szumma jel utáni második tényezőben fedezhetünk fel. Megtehetjük, hogy minden pontban vizsgáljuk a mintát, azonban ebben az esetben a program rendkívül lelassul, hiszen ha minden pixelt megengedünk, akkor nagy valószínűséggel a hátteret vizsgáljuk, és bár ezt “lenullázzuk” a súlyozásnál, de nagyon sok mintavételre van szükségünk a Monte-Carlo módszernél, ami lelassítja az eljárást. Ha viszont csak az egyhez közeli értékeket engedjük meg, a program nagyon nehezen talál elfogadható pixelt. Ez az állítás természetesen azokra az esetekre vonatkozik, amikor a kiválasztott mintázat nem ideális, azaz elektronmikroszkópos képek esetét tekintve a szkennelés, a detektor leárnyékoltsága vagy a mintázat egyenetlensége következtében. A megoldást abban találtuk meg, hogy egy bizonyos vágási érték felett kezdtük el a boxnövesztést és nem súlyoztuk a tömegeket, hanem egyenrangúnak tekintettük őket. A vágási érték 0.5-0.6 körüli megválasztása esetén a kiértékelő program már felhasználhatóságát tekintve gyorsan működött. Ez tulajdonképpen a ![]() feltételezés olyan esetekre, ahol a GM érték a vágási értéknél nagyobb.
feltételezés olyan esetekre, ahol a GM érték a vágási értéknél nagyobb.
2.4. Az irányfüggés vizsgálata
A kontaktusok felszínéről készített SEM felvételek vizsgálatakor számos esetben azt tapasztaltuk, hogy a mintázatok irányfüggést mutatnak, (pl. egy bizonyos irányban elnyúlnak mintegy az emberi kéz rajzolata, vagy szabályos orientációjú négyszögletes alakzatok figyelhetők meg). Ez rendkívül izgalmas problémának ígérkezik, hiszen feltehető, hogy ezen irányfüggő alakzatok kialakulása kristálytani eredetű, bár az sem zárható ki, hogy a félvezető-fém kontaktusok készítésekor keletkezett hibák (csiszolás, párologtatás iránya) okozza ezt az irányfüggést. Mindenképpen érdekes elméleti kérdéseket vet fel az az eset, melynél felvetődött egy irányfüggő perkoláció-elméleti gondolat. Módszereinket erre az esetre úgy módosítottuk, hogy korreláció analízisünknél csak az egyik irányban növesztjük a boxokat, így a mintázat statisztikai metszetének dimenzióját kapjuk. Egy kétdimenziós objektum, pl. egy kör minden irányból egydimenziósnak mutatkozik. Nyilván itt is egy szögeloszlás-dimenzió görbével lehet jellemezni ezt az esetet. Ezzel az eljárással minden eddigi módszerünk, többek között a durva és a puha szegmentációs gondolatsor is átalakítható.
3. Au/Pd/GaAs kontaktus vizsgálata
Tömegspektrométerrel egybeépített pásztázó elektronmikroszkóppal gallium-arzenid hordozóra leválasztott Au (85 nm)/Pd (50 nm) fémezést vizsgáltunk hőkezelés során. Az elsőként általunk javasolt mérési eljárás lehetővé tette, hogy egyidőben regisztráljuk a vegyület-félvezető termikus bomlásából keletkező, s nagy gőznyomása miatt a felületről eltávozó illékony komponens mennyiségét, valamint a minta felületi morfológiájának változását a hőkezelés során. Az alkalmazott elektronmikroszkóp japán gyártmányú, JEOL JSM-T20 típusú pásztázó elektronmikroszkóp, amelyben az elektronoptikai berendezés és a tárgy 10-3 Pa nyomású, rotációs és diffúziós szivattyúk által előállított vákuumban van. Azért, hogy a hőkezelése közben (’in situ’ módon) is lehessen a minták felületéről SEM képeket készíteni, külön erre a célra készített fűthető mintatartót alkalmaztunk [12,13,14]. Az EGA mérésre (Evolved Gas Analysis – illékony komponens analízis) Q100C (ATOMKI) típusú, Faraday-kalitkával ellátott kvadrupól tömegspektrométer szolgált. Illékony komponens alatt a GaAs esetében arzént, InP esetében foszfort, GaSb esetében antimont kell érteni. Az általunk kifejlesztett mérési összeállítás blokkvázlata a 4. ábrán látható.

4. ábra. A tömegspektrométerrel egyesített pásztázó elektronmikroszkópos mérőberendezés blokkvázlata
A vizsgált minták (100) orientációjú, egykristály hordozóra gőzfázisú leválasztással készített epitaxiális rétegek voltak. A GaAs szeletek n-típusú (Sn-nal adalékolt) 2-3x1023 m-3 adalékanyag-koncentrációval rendelkeztek. A fémréteg leválasztása előtt a GaAs szeletek megfelelő kémiai tisztításon és előkészítésen estek át. A fémezést wolfram csónakos ellenállásfűtésű párologtatóval vittük fel a hordozóra.
A hőkezelést az előzőekben ismertetett berendezésben végeztük. A mintát 30 ° C/perc felfűtési sebességgel 630 ° C-ig felfűtve tömegspektrométerrel mértük a hőkezelés során az arzén kipárolgását, míg a pásztázó elektronmikroszkóppal BEI üzemmódban fényképfelvételeket készítettünk a minta felszínéről. A fényképfelvételek elemzése során megállapítottuk, hogy a minta felületi rajzolata a hőkezelés során bizonyos esetekben (a jelentékeny arzénkipárolgás tartományában) fraktáljellegű, vagyis önhasonló volt. Sikerült kapcsolatot találnunk a minták fraktáldimenziója és a kipárolgási görbe jellegzetes pontjai között [15].
Korábbi vizsgálataink során a mintázatokat kétfázisúnak – azaz egy világosabb és egy sötétebb fázisból összeállónak – tekintettük, s a minta fraktálanalízisét is így végeztük
[16, 17]. Az Au/Pd/GaAs szerkezeten néhány fényképfelvételen ellenben egyértelműen három fázis különböztethető meg. A mintázat fraktáljellemzők szerinti kiértékelésére a puha szegmentációs eljárást alkalmaztuk.
Feladatunk tehát a kiértékelés során a három klaszter (legyenek relatív árnyalataik után egyszerűen csak fekete, szürke és fehér színűeknek elnevezve) jellemző intenzitásértékeinek meghatározása volt. Ezt egy saját készítésű bitmap-néző programmal valósítottuk meg, amelynek segítségével a képernyőn megjelenített bitmap képen az egérkurzorral a kívánt képpontra kattintva a program megadja annak szürkeségértékét (0-255). Az általunk leginkább jellegzetesnek ítélt fehér, szürke és fekete klaszterekhez tartozó intenzitásértéket feljegyeztük. Vizsgálataink során háttérnek minden alkalommal a legsötétebb (fekete) klasztert jelöltük ki, míg fraktálmintázatnak egyszer a szürke, majd a fehér, végül mindkét fázist együttesen tekintettük. Miután megkaptuk a jellemző vi értékeket, a képet egy szintén saját készítésű súlyozó programmal dolgoztuk fel, amely a GM függvényt használja a kiértékeléshez.
A mintáról 500 ° C-os hőmérsékleten készített SEM felvételen jól elkülöníthetően látszik a három fázis (5. ábra). A klaszterekhez tartozó jellegzetes vi értékek: vfekete=70, vszürke=160, vfehér=245. Egyenként a fehér, csepp alakú részekből összeálló, illetve a szürke, négyszögekből felépülő klaszterek fraktáldimenzióját határoztuk meg, majd a fehér és a szürke mintázat együttes fraktáldimenzióját is az 1 - Gfekete(X) összefüggés alkalmazásával.

5. ábra. Au (85 nm)/Pd (50 nm)/ GaAs (100) fémezés képe a hőkezelés közben 500 °
C-on, 400x nagyítással.
A trapéz jellegű szürke mintázatok fraktálmértéke a hőmérséklet függvényében L=32-es boxméret esetén a 6. ábrán látható. A kialakult görbe és a mások által mért fajlagos kontaktus ellenállás közötti összefüggést állapítottunk meg. Véleményünk szerint a 6. ábra épp a kontaktus vezetőképességével hozható összefüggésbe. Ennek oka az, hogy feltételezésünk szerint a trapéz jellegű mintázat felelős az ohmos kontaktus kialakulásáért, ezért nem az egész felület vesz részt a vezetésben. A hőmérséklet függvényében változik a trapéz jellegű mintázat fraktálmértéke, 360 ° C előtt a felület homogén volt, majd megjelentek a különböző méretű trapéz alakú mintázatok, melyek 620 ° C környékén szemmel láthatóan megolvadtak. Ez összecseng azzal a tapasztalattal, hogy a kontaktust túl is lehet hőkezelni.
A görbe maximumához tartozó hőmérséklet jó közelítéssel megegyezik Lamouche és munkatársai [18] által mért optimális kontaktus ellenálláshoz tartozó hőmérséklettel.
Az Au/Pd/GaAs minta elpárolgó alkotóelem veszteség - hőmérséklet diagramját mutatja a 7. ábra. Az Au/Pd/GaAs kontaktus EGA-diagramjában az arzén kipárolgás két jellemző csúcsát figyeltük meg. Az első csúcs a palládium és GaAs közötti reakciónak köszönhető, miközben a második csúcs az arany galliummal való kölcsönhatásának tulajdonítható.
Lamouche és mások [18] azt tapasztalták, hogy ennek a szerkezetnek a fajlagos kontaktusellenállása 360 ° C felett az ohmos irányába tendál. Ők kb. 500 ° C-nál érték el a fajlagos kontaktusellenállás optimumát. Lamouche hasonló módon hőkezelt minta elektromos vizsgálatai alapján az így készült kontaktusokat ohmos kontaktusnak minősítette.
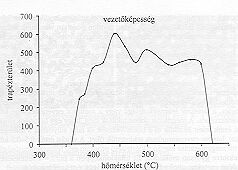
6. ábra. A trapéz jellegű mintázat fraktálmértéke a hőmérséklet függvényében
A trapéz jellegű mintázat fraktálmértékének maximuma 450 ° C körül alakult ki (6. ábra), mely hőmérséklet az Au/Pd/GaAs szerkezet második, arany okozta arzén kipárolgási csúcsa kezdete előtti hőmérséklet értéknek felel meg a 7. ábrán. Ezekből az eredményekből is levonható az a következtetés, hogy a jó ohmos kontaktusok előfeltétele, hogy a GaAs bomlását megakadályozzuk.

7. ábra. Au/Pd/GaAs minta elpárolgó arzén veszteség - hőmérséklet görbéje
4. Összefoglalás
Kísérleti munkánk során összefüggést találtunk a felületről készített SEM képek fraktáltulajdonságai és más fizikai paraméterek – mint például a hőmérséklet és a BV komponens (As ill. P) kipárolgása – között. Cikkünkben számos matematikai kiértékelési eljárást bemutattunk, melyek közül egyet egy példával (Au/Pd fémezés GaAs hordozón) is illusztráltunk.
Elért eredményeink az anyagszerkezeti vizsgálatok tükrében továbbvihetők. A továbbiakban vizsgálni szeretnénk, hogy a tapasztalt fraktáltulajdonságok – melyek a hőkezelés során a kontaktus szerkezetében létrejövő anyagszerkezeti változásokra vezethetők vissza – milyen kapcsolatban vannak a kontaktus elektromos (kontaktusellenállás) és szerkezeti tulajdonságainak megváltozásával. Itt jöhet szóba a mélységi anyagvizsgálat, az elektromos mérések és a perkolációs modell alkalmazása. További matematikai/számítógépes eljárásokat is szeretnénk kidolgozni, valamint a meglévőket finomítani a hőkezelés során a kontaktuson megfigyelt folyamatok fizikai hátterének pontosabb leírása érdekében.
Köszönetnyilvánítás
Szeretnénk köszönetet mondani Dr. Kovács Balázsnak és Dr. Máté Lászlónak a munkánk során adott értékes tanácsaikért, szakmai támogatásukért.
Irodalom