Fizikai Szemle honlap |
Tartalomjegyzék |
Fizikai Szemle 2001/7. 204.o.
FIZIKAI FOLYAMATOK AZ INTRACELLULÁRIS JEL ÉS ENERGIAÁTVITELBEN
Forgács Gábor
Szilárdtestfizikai Kutató Intézet, Budapest
Clarkson University, Potsdam, NY, USA
University of Missouri, Columbia, MO, USA
Ahhoz, hogy egy sejt normálisan működhessen, szüntelen kapcsolatot kell fenntartania környezetével. Ez azt jelenti, hogy a szomszédos sejtektől valamint a sejtközi állományból (az extracelluláris mátrixból) kap ingereket. A beérkező jeleket felfogja, továbbítja a sejt különböző részeibe, és végül fizikai vagy kémiai úton reagál rájuk. Mindehhez a sejtnek kifinomult jelzőrendszerrel kell rendelkeznie.
Egy ilyen jelzőrendszer első eleme egy antenna, amely felfogja a beérkező jeleket. A jel maga tipikusan valamilyen kémiai elem (úgynevezett ligandum) formájában érkezik. Az antennát a sejt felületén elhelyezkedő receptorok alkotják, melyek az esetek többségében transzmembrán fehérjék. A környezetből érkező inger tehát egy receptor-ligandum kötés kialakulását eredményezi. Ez a receptor-fehérje konformációjának megváltozásához vezet. A receptor, lévén transzmembrán fehérje, intracelluláris végződésén keresztül a sejt belsejébe továbbítja a változást (ami lokálisan fellépő mechanikai deformációkban manifesztálódhat). Hogy innen a jel hogyan jut el végső rendeltetési helyére, a mai sejtbiológiai kutatások egyik alapvető kérdése.
A legtöbb jelvezetéssel foglalkozó biológus úgy gondolja, hogy egy tipikus intracelluláris szignalizációs trajektória enzimreakciók kaszkádján keresztül, vagyis kizárólag biokémiai úton valósul meg. Sajnos a legtöbb dokumentált szignalizációs trajektória csak részben feltérképezett. Legtöbbször csak a kezdeti és végső reakciók ismertek, a közbülső folyamatokat kérdőjelek reprezentálják. A nehézséget az jelenti hogy egy tisztán biokémiai jelpálya sokszor feltételezi akár tizenöt enzim jól összehangolt kölcsönhatását [1-3]. Hogy ezek időben és térben hogyan képesek megtalálni egymást, honnan tudják, hogy mi a kaszkádon belüli kémiai reakciók helyes sorrendje nem feszegetett kérdések.
Egyre több kutató látja úgy, hogy megbízható intracelluláris jelátvitel nem jöhet létre pusztán biokémiai folyamatok láncreakcióján keresztül [4-6]. Szükségeltetik valamiféle robusztus mechanizmus, ami nem kizárólag a jelvezető molekuláknak a sejten belüli térben (a citoplazmában) történő véletlenszerű bolyongásán alapul. Ennek a felismerésnek az ad alapot, hogy közismert tény, miszerint a transzmembrán receptor-fehérjék intracelluláris végződéseiken keresztül kapcsolódnak a citoszkeletonhoz, a sejt belsejének architektúráját meghatározó vázhoz. A citoszkeletont aktin, mikrotubulus és intermediális filamentumok alkotják. Ezek a filamentumok1 az egész sejtet behálózzák (beleértve a sejtmagot), struktúrájukban rendezetlen pókhálóhoz hasonlíthatók. Egy ilyen csatolt hálózat ideális jelölt arra, hogy pókhálóhoz hasonlóan mechanikai úton továbbítson információt.
Ma már széles körben elfogadott álláspont, hogy a sejt geometriai tulajdonságain túl a citoszkeleton számos egyéb sejtfunkció elvégzésében is részt vesz. Így kimutatható, hogy aktin-filamentumok hiányában, csontképző sejtekben nem működnek bizonyos gének [7]. Amennyiben egy cadherin (Ca függő sejtfelületi adheziós molekula) intracelluláris, citoszkeletonnal való kapcsolata sérül, a molekula nem tudja ellátni fiziológiás szerepét. Ennek következtében az adott sejtekből álló szövet széteshet [8]. Közvetlenebb bizonyítékot a citoszkeletonnak az intracelluláris szignalizációban betöltött szerepére B. Nicklaus és munkatársainak kísérletei szolgáltatnak. Kimutatták, hogy amennyiben a sejtosztódás során kialakuló mitótikus orsóban a mikrotubulusok által a kromoszómákra kifejtett feszültség egy alsó kritikus érték alatt marad, a sejtosztódás leáll. Ha a feszültség akár külső beavatkozás útján (mikropipetta segítségével) helyreáll, a sejtosztódás folytatódik [9]. Közismert az is, hogy a jelvezetésben aktív szerepet játszó enzimek (kinázok és foszfotézek) nagy része a citoszkeleton mentén lokalizált [6].
A fentiekből feltételezhető, hogy a citoszkeleton valamilyen módon aktív részese a sejten belüli jelvezető apparátusnak. Ezt ma már egyre kevesebben vonják kétségbe. Az azonban, hogy a citoszkeleton milyen konkrét mechanizmuson keresztül fejti ki hatását a jelek továbbításában, komoly erőfeszítések ellenére is még mindig nyitott kérdés.
Jelen dolgozatban a szerző az intracelluláris szignalizáció és energiaátvitel egy lehetséges modelljét kívánja vázolni. A modell a citoszkeleton ama tulajdonságán alapul, hogy az a sejten belül egy globálisan összefüggő hálózatot alkot. Ily módon a citoszkeleton elősegítheti a jelvezető molekulák sokkal fókuszáltabb kölcsönhatását és mozgását a hálózatot alkotó filamentumok mentén (kikerülvén az organellumok által képzett esetleges akadályokat). Másrészt, lévén csatolt rendszer, a citoszkeleton képes tisztán mechanikai energiaátvitelre is. Így lehetőség nyílik a biokémiai és mechanikai szignalizációs folyamatok kombinálására, ami az információ továbbításának még hatékonyabb és változatosabb módozatainak kihasználását biztosíthatja.
Konkrétan két szignalizációs mechanizmust fogunk vizsgálni. Az egyik a lehetséges legegyszerűbb biokémiai jelvezető trajektória; egyetlen molekula (például kinőz) révén alakul ki. Itt azt kérdezzük, mi az az átlagos idő, ami alatt egy molekula - mely vélhetően valamiféle jelet szállít - véletlen bolyongást végezve a citoszkeletont alkotó filamentumok mentén, először jut el a sejtmagig. Ezt az időt az "Első Áthaladás Idejének" (EÁI) nevezzük (First Passage Time). Az EÁI-val sokszor helytelenül felcserélt fogalom a diffúziós idő. Ez utóbbi ugyancsak véletlenszerű bolyongást végző részecskével kapcsolatos. Míg azonban az EÁI átlagos idő adott célponttól mért rögzített távolság megtételéhez szükséges, addig a diffúziós idő az a rögzített idő, ami alatt izotróp módon bolyongva a részecske bizonyos átlagos távolságot fut be. Esetünkben a távolság és a célpont adott, így az EÁI a releváns mennyiség.

A második esetben azt kérdezzük, mennyire effektív a citoszkeleton mentén történő mechanikai energiaátvitel. Ekkor a citoszkeletont alkotó filamentumokat viszkózus közegbe (citoplazmába) ágyazzuk és a sejt felületén ható mechanikai perturbációnak tesszük ki. Az energiaátvitel hatékonyságát a citoszkeleton, illetve a sejt bizonyos fizikai tulajdonságainak függvényében vizsgáljuk.
Fő célunk azt megmutatni, hogy az adott sejtfunkció (információátvitel) ellátásához szükséges biológiai specificitás nemcsak biokémiai úton biztosítható, hanem az élő sejt fizikai tulajdonságainak módosításával is elérhető. Ha ez valóban így van, azt a következtetést vonhatjuk le, hogy a sejten belüli biokémiai és mechanikai eredetű regularizációs mechanizmusok molekuláris skálán nem megkülönböztethetők.
A modell
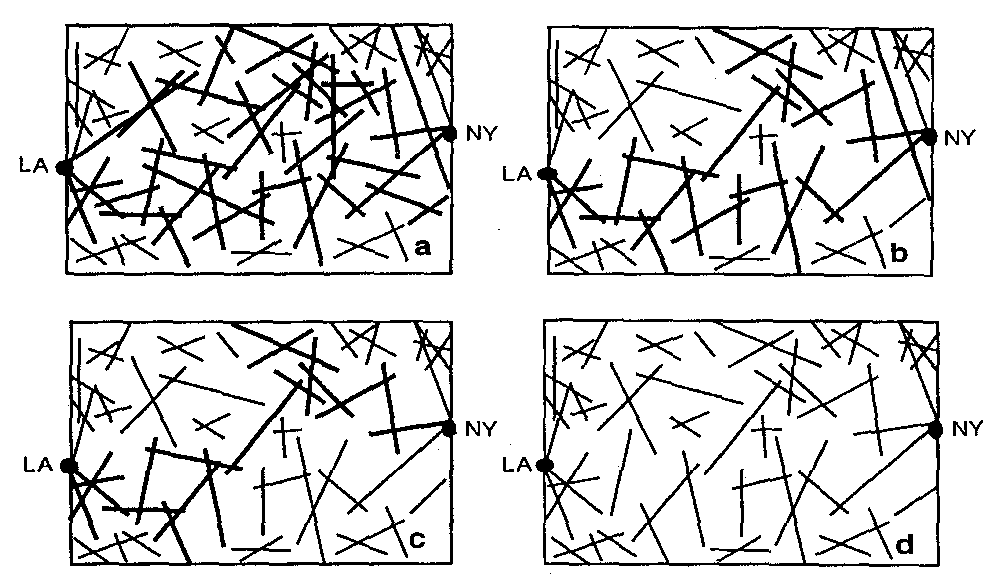
Modellünkben feltételezzük, hogy a citoszkeleton egy rendezetlen perkolációs hálóval reprezentálható. A perkoláció széles körben elfogadott és használt fogalom. Lényegét az 1. ábra szemlélteti. 2 In vitro kísérletek igazolják, hogy a citoszkeleton fontos részét képező F-aktin (azaz filamentumos aktin) valóban perkolációs hálót képez [11,12]. (Egy F-aktin-filamentum, mint polimér lánc, G-aktin molekulákból, mint monomerekből áll össze.)
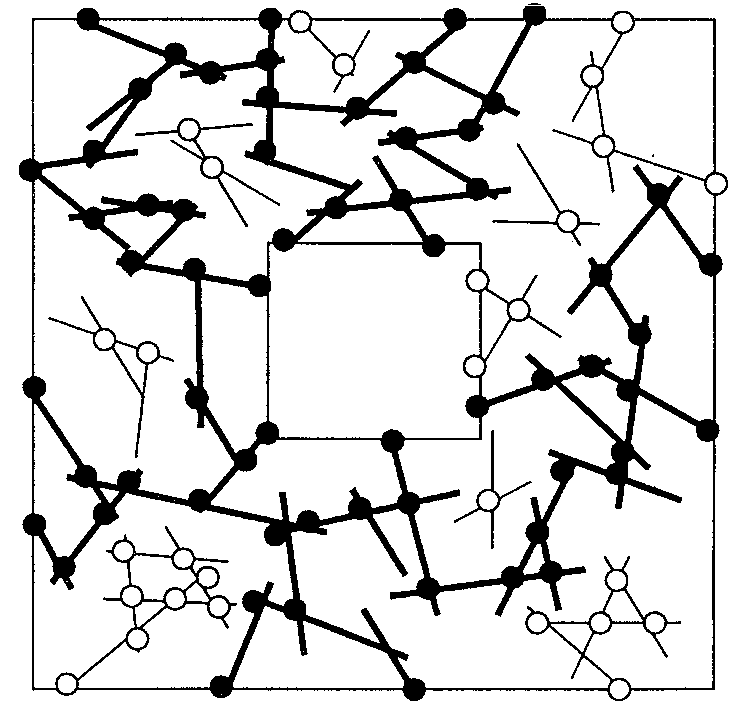
Intracelluláris szignalizációs modellünket egy modellsejtre fogjuk alkalmazni, melynek kétdimenziós vetülete a 2. ábrán látható. A sejtet egy 10 mikron oldalhosszúságú kocka határolja. Ennek közepén helyezkedik el a sejtmagot reprezentáló 5 mikron oldalhosszúságú másik kocka. A különböző filamentumokat merev pálcákkal helyettesítjük. Jelen dolgozatban csak egyféle filamentumot tekintünk, melynek átmérőjét 10 mikronnak, hosszát pedig 0,5-1,5 mikronnak választjuk. Az ilyen filamentumok leginkább aktin-láncokra hasonlítanak. Az átmérő alkalmas megválasztásával más típusú filamentumok is modellezhetők. Mivel az aktin-filamentumok perzisztencia-hossza (az a hosszméret, melyen belül egy polimérlánc merevnek tekinthető) meghaladja a 10 mikront, merev pálca közelítéscink helyénvaló. Mindegyik pálca helyzetét a térben hat paraméter adja meg. Három az egyik végpont koordinátáit definiálja, egy megadja a pálca hosszát, míg két szög a pálca orientációját rögzíti. Az így definiált pálcákból álló rendezetlen hálót számítógépen generáljuk, a hat paraméter mindegyikének értékét független véletlen számokkal határozzuk meg.
A rendetlen háló szimulálásakor a következő szabályokat használjuk. A pálcák nem hatolhatnak át egymáson. Ha két filamentum között a legrövidebb távolság bizonyos minimális (0,2 mikron) méretnél kisebb, azt mondjuk, hogy azok egy csomóponton keresztül egymáshoz vannak csatolva. Amikor eme csatolás konkrét fizikai tulajdonságaira van szükségünk (lásd alább), a csomópontot a filamentumok közti legrövidebb távolságot meghatározó két pontot összekötő rugókkal reprezentáljuk. A filamentumok, illetve pálcák a sejtfelület és a sejtmag között helyezkednek el. Ebben a munkában a sejtmagon belüli jelenségekkel nem foglalkozunk. Speciális csomópontok felelnek meg azoknak a helyeknek, ahol egy pálca vagy a sejtfelületet (belépési pont) vagy a sejtmagot (kilépési pont) metszi.
Első áthaladás ideje a citoszkeleton mentén
A citoszkeleton mint perkolációs háló. Feltételezéscink szerint egy molekula akkor tud jelet továbbítani a sejtfelülettől a sejtmagig, ha az összefüggő perkolációs hálót képező citoszkeleton filamentumai mentén diffúziós
2. ábra A modell-sejt kétdimenziós vetülete. A sejtfelület a sejtmaggal összecsatoló filamentumokat vastag vonallal szemléltetjük. A perkolációs hálóhoz tartozó csomópontokat teli, míg az egyéb csomópontokat üres körökkel jelöljük. 3. ábra. Annak P valószínűsége, hogy egy tetszőlegesen kiválasztott filamentum az összefüggő részhalmazhoz tartozik. Az ábrán feltüntetett mindegyik pont - filamentum-koncentrációtól függően - 30-250 futtatásra vett átlagot jelent.
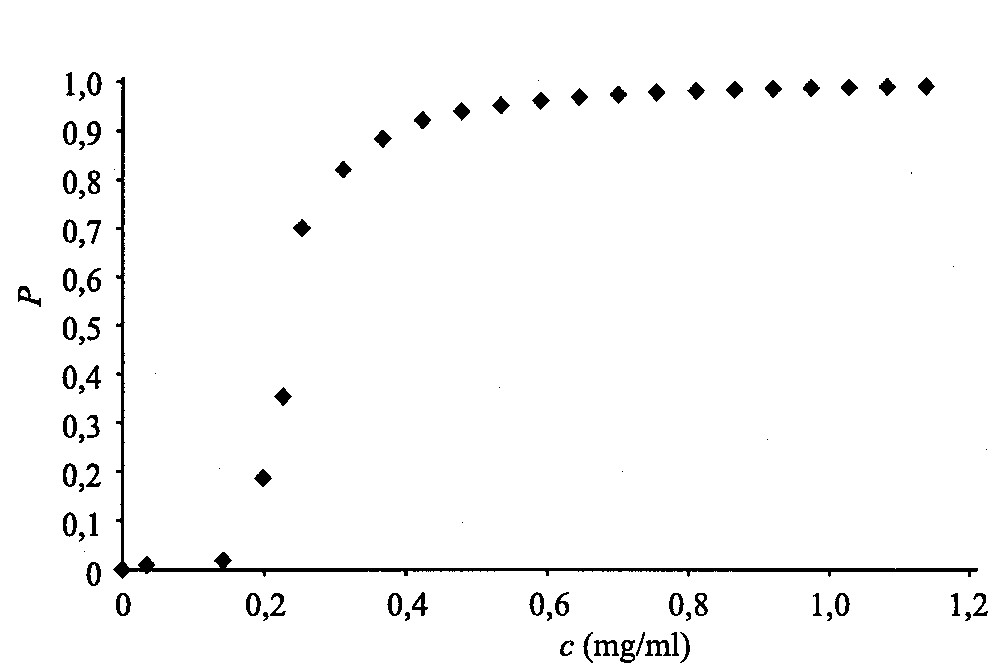
mozgást tud végezni. Kis c koncentráció esetén a filamentumok nem képeznek összefüggő rendszert. Nagy c esetén számos olyan folytonos útvonal van, melyek mentén egy egyébként a filamentumokon mozogni képes molekula, az egyik filamentumról a másikra jutva, elérheti célpontját, azaz a sejtmag felületét. (E dolgozatban feltételezzük, hogy ha a jel eljut a sejtmag felületéig, akkor valamilyen más mechanizmus segítségével a megfelelő génig, illetve az annak tevékenységét szabályozó promoterig is eljut.) A filamentum-koncentráció szélsőséges értékei között létezik egy Ckr kritikus koncentráció, melynél a sejtfelület és a sejtmag először kerül közvetlen kapcsolatba, vagyis a filamentum-rendszer összefüggővé lesz. A koncentráció eme értékét nevezzük perkolációs küszöbnek
[10]. Ckr felett véges annak P valószínűsége, hogy egy tetszőlegesen kiragadott filamentum a rendezetlen rendszer ama részhalmazához tartozik, melyet egymáshoz kapcsolódó filamentumok alkotnak. (Mint az a
2. ábráról is látszik, nyilvánvalóan Ckr felett számos olyan filamentum van, mely nem tartozik az összefüggő részhalmazhoz.) P változását a filamentum-koncentráció függvényében a
3. ábra szemlélteti. Mint látható, az általunk használt modell-filamentumok esetében Ckr 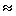 0,2 mg/ml. Egy tipikus élő sejtben az F-aktin-koncentráció legalább 5 mg/ml, vagyis lényegesen a perkolációs küszöb felett van
[13]. (Szigorúan vett termodinamikai határesetben, ami végtelen kiterjedésű és végtelen sok filamentumot tartalmazó rendszert jelent, Ckr jól meghatározott értéket vesz fel [10].)
0,2 mg/ml. Egy tipikus élő sejtben az F-aktin-koncentráció legalább 5 mg/ml, vagyis lényegesen a perkolációs küszöb felett van
[13]. (Szigorúan vett termodinamikai határesetben, ami végtelen kiterjedésű és végtelen sok filamentumot tartalmazó rendszert jelent, Ckr jól meghatározott értéket vesz fel [10].)
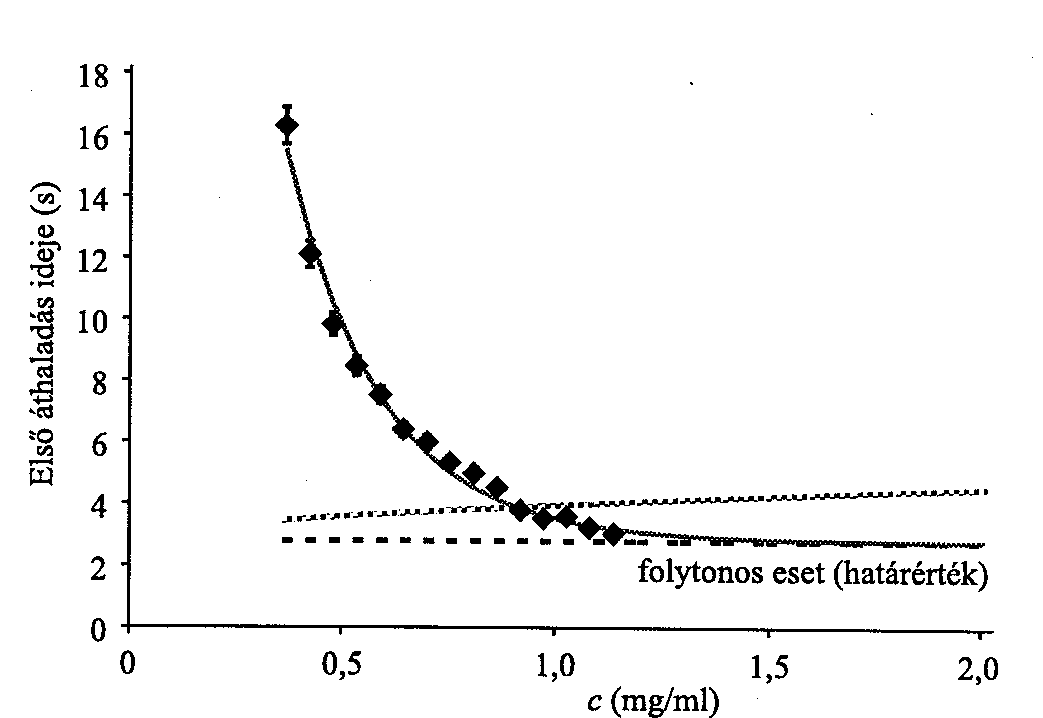
4. ábra. Első Áthaladás Ideje (EÁI) a rendezetlen filamentum-rendszer mentén (a szimulációval kapott pontokat összekötő görbe) a filamentum-koncentráció függvényében. A függőleges hibavonalak azt mutatják, hogy a koncentráció növelésével a fluktuációk csökkennek. A diszkrét filamentum-rendszerre kapott EÁI konvergál a folytonos citoplazma esetében kapott értékhez. (A szimulációkban D1/D3 = 0,93 és D3 = 10-7 cm2/s értékeket használtunk. Itt D1 és D3 az egy-, illetve háromdimenziós diffúziós állandó.) Az Ogston-elméleten alapuló eredményt (lásd a szöveget) vastag vonallal ábrázoljuk.
EÁI a filamentum-koncentráció függvényében. Az EÁI meghatározása egy, a 2. ábrán szemléltetett rendezetlen rendszerben rendkívül bonyolult feladat.3 Röviden, feladatunk annak a T időnek kiszámítása, mely ahhoz kell, hogy a filamentumok mentén bolyongó molekula először érjen egy belépési pontból egy kilépési pontba. Sajnos T meghatározásához szükségünk van valamennyi Ti-re. Itt Ti az EÁI értéke, az i-edik csomópontból indulva. A különböző csomópontokra vonatkozó Ti-k (beleértve a belépési pontokat) egy lineáris egyenletrendszernek tesznek eleget, mely numerikusan megoldható. (N számú pálca esetén a csomópontok átlagos száma 3N. Numerikus szimulációnkban N értéke maximálisan 35000, ami 2,2 mg/ml F-aktin-koncentrációnak felel meg.) Az így számított Tfilamentum-koncentrációtól való függését a 4. ábra szemlélteti. (Mivel sok belépési pont van, a függőleges tengely mentén a valamennyi belépési pontra vonatkozó átlagos T-t tüntettük fel.) Mint várható, c alacsony értékeire az EÁI nagy (Ckr alatt definíció szerint végtelen), de c növelésével rohamosan csökken. A 4. ábráról levonható talán legmeglepőbb következtetés akkor adódik, amikor összehasonlítjuk EÁI diszkrét filamentumok mentén, illetve folytonos térfogatban történő bolyongás esetén számított értékeit. Amennyiben a használt folytonos térfogat megegyezik azzal a térrésszel, amibe a diszkrét filamentumok rendszerét beágyazzuk, valamint a háromdimenziós és egydimenziós diffúziós állandókat azonosnak választjuk, EÁI fenti két értéke között már c = 1,5 mg/ml-nél (vagyis jóval a fiziológiás határ alatt) nincs számottevő különbség. 4
Modellünk nagy előnye nyilvánvaló, ha a bolyongást akadályozó, a valós sejtben mindig jelenlévő organellumokat (például mitokondrium, endoplazmás retikulum, Golgi-apparátus stb.) figyelembe vesszük. A 4. ábrán feltüntettük Jones és Luby-Phelps eredményét [16], melyet a szerzők, méréseik kiértékelésekor kaptak, amihez Ogston elméletét [17] használták. Jones és Luby-Phelps próbatest citoplazmában történő diffúzióját vizsgálták és feltételezték, hogy a citoszkeleton (mint maga is egyfajta organellum) ahelyett hogy segítené, akadályozza azt.
Mint az ábráról látható, ilyen esetben EÁl már viszonylag kis filamentum-koncentráció esetén is meghaladja a filamentumok mentén történő bolyongásra vonatkozó értéket. Könnyen elképzelhető, mennyivel rosszabb lenne a helyzet, ha a többi organellumot is figyelembe vennénk.
Mechanikai energiaátvitel a citoszkeleton mentén
Energiaátvitel a sejt fizikai tulajdonságainak függvényében. Mint mar említettük, tudvalévő, hogy a jelvezetésben résztvevő számos molekula van közvetlen kapcsolatban a citoszkeletonnal. Azt is lehet tudni, hogy ezen molekulák között bekövetkező kémiai reakciók sokszor a citoszkeleton közreműködésével mennek végbe. Ehhez nyilván szükségeltetik, hogy a reakciókomponensek egymásra találjanak, vagyis a filamentumok mentén mozogni tudjanak. Ennek egyik lehetséges mechanizmusát tárgyaltuk a fentiekben. Kémiai reakció következtében egy protein tipikusan konformációs változáson megy keresztül, vagyis egyik energiaállapotból a másikba jut. Egy fizikus (de nem feltétlenül biológus) számára kézenfekvő az a gondolat, hogy konformációváltozás megfelelő mechanikai energiaközléssel is kiváltható. A közelmúltban elvégzett kísérletek összhangban látszanak lenni ilyen feltételezéssel [18-20].
A továbbiakban a mar ismertetett modell segítségével, illetve annak triviális módosításával megvizsgáljuk, mennyire alkalmas a citoszkeleton mechanikai energia továbbítására a célból, hogy a rajta elhelyezkedő jelzőmolekulákat biológiailag releváns funkciók ellátására aktivizálja. Az 2. ábrán vázolt citoszkeleton-modellt most a belépési pontoknál mechanikai perturbációnak vetjük alá. A sejtfelülettel érintkező pálcákra időben periodikusan változó forgatónyomatékkal hatunk. A motivációt ehhez az eljáráshoz Rychly és munkatársai által végzett kísérletek szolgáltatták [20]. Ezek a szerzők mágneses golyókat erősítettek integrinekhez, majd a vizsgált rendszert periodikus mágneses térbe helyezték.' Ezután azt vizsgálták, milyen kémiai változások következnek be a sejt belsejében a külső mágneses mező frekvenciájának függvényében.
Az EÁI számolásánál a citoszkeletont merev perkolációs hálónak tekintettük. Most a külső hatás miatt a filamentumok mozognak. A sejtfalhoz rögzített filamentumok csak forogni képesek, de a sejten belül elhelyezkedő filamentumok mind forgó, mind pedig transzlációs mozgást képesek végezni. Ahhoz, hogy a felületen alkalmazott periodikus jel tovább tudjon terjedni, a pálcákat a csomópontokban elhelyezett rugókkal csatoljuk egymáshoz. Az egész rendszer a viszkózus citoplazmában mozog. A citoplazma
 viszkozitása függ a sejttípustól és a víz
viszkozitása függ a sejttípustól és a víz
 v, értékének többszöröse is lehet. A filamentumok transzlációs mozgását a tömegközéppontra felírt Newtonegyenletek írják le. Az egyes filamentumokra a viszkozitásból eredő súrlódási erőn kívül hatnak a szomszédos
v, értékének többszöröse is lehet. A filamentumok transzlációs mozgását a tömegközéppontra felírt Newtonegyenletek írják le. Az egyes filamentumokra a viszkozitásból eredő súrlódási erőn kívül hatnak a szomszédos
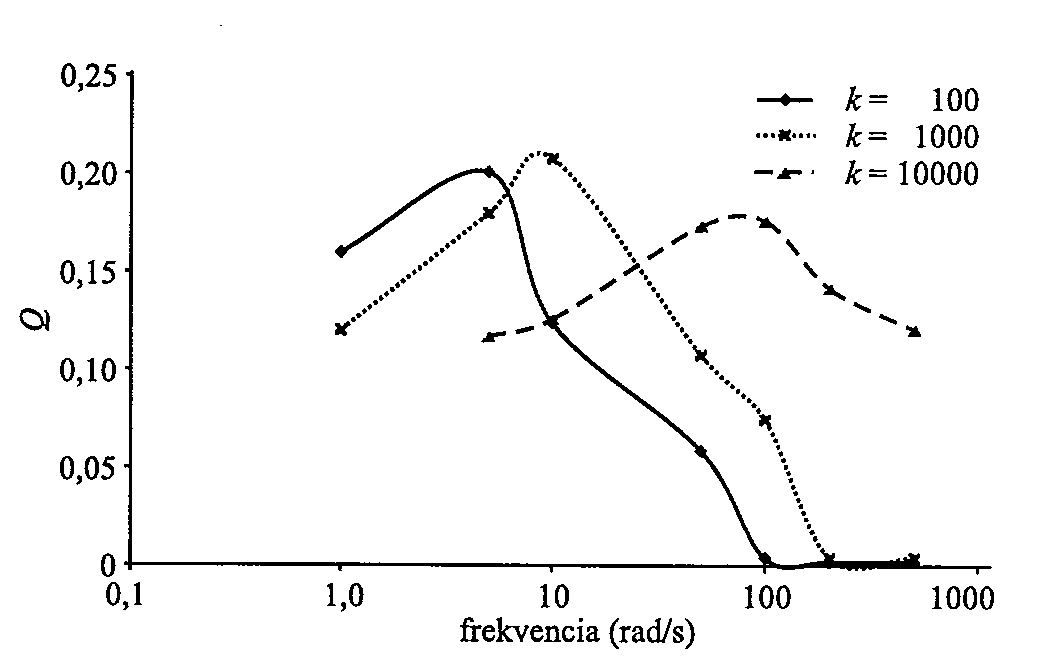
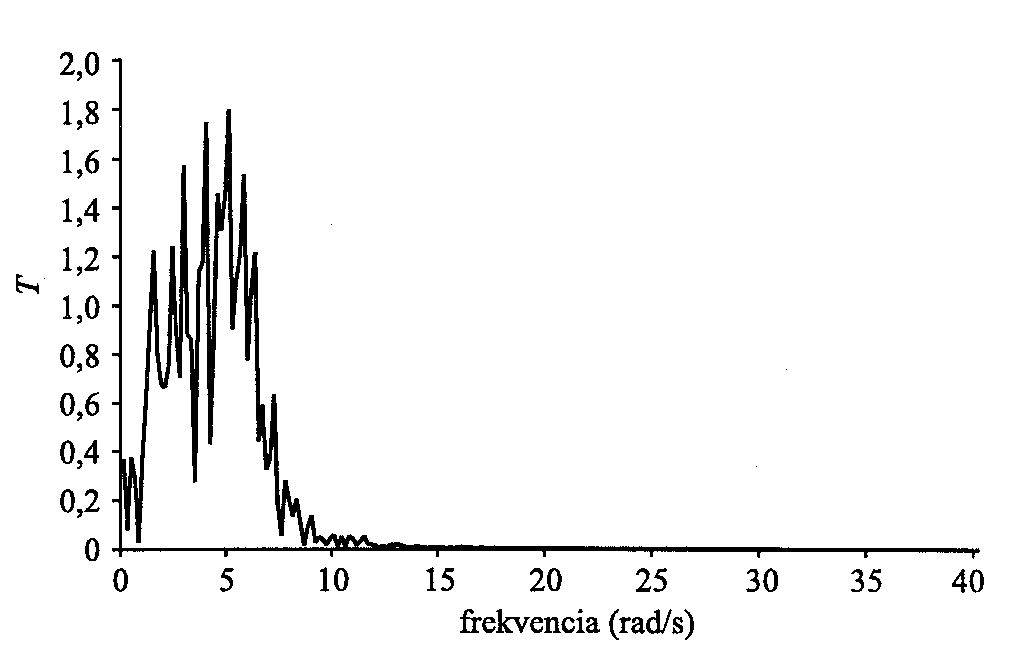
5. ábra. A Q átviteli tényező a gerjesztő frekvencia függvényében különböző k rugóállandók esetében. Az ábra a
 = 10
= 10 v -re vonatkozik, ahol
v -re vonatkozik, ahol
 és
és  v a citoplazma, illetve a víz viszkozitása.
v a citoplazma, illetve a víz viszkozitása.
 növelésével Q csökken.
növelésével Q csökken.
filamentumok által kifejtett erők is. Viszonylag könnyen belátható, hogy ezekben a mozgásegyenletekben az inerciális tag elhanyagolható [21]. A forgó mozgás a súrlódási taggal kiegészített Euler-egyenletekkel tárgyalható, melyeket cél szerű a pálcákhoz rögzített koordinátarendszerben felírni [22]. A transzlációs és forgó mozgást leíró egyenletek csatoltak, ez a számolásokat lényegesen megnehezíti. Az egyenleteket numerikusan oldottuk meg, a Billeter és Pelcovits által kidolgozott speciális algoritmust használva [23].
A belépési pontoknál alkalmazott forgatónyomaték hatására, a filamentumokat összecsatoló rugók miatt a mechanikai energia a citoszkeleton mentén fog terjedni. A sejtmaghoz így eljuttatott energia átvitelének hatékonyságát egy átviteli tényezővel fejezzük ki. Ezt a kilépési és belépési pontokban elhelyezkedő pálcákhoz csatolt rugókban tárolt energiák hányadosával definiáljuk és Q-val jelöljük. Az
5. ábrán ezt a mennyiséget a periodikus forgatónyomaték frekvenciájának a függvényében, különböző k rugóállandókra tüntettük fel. (A citoplazma viszkozitása
 = 10
= 10 v.) Látható, hogy minden rugóállandóhoz tartozik egy jól meghatározható
v.) Látható, hogy minden rugóállandóhoz tartozik egy jól meghatározható  m frekvencia, melynél az átvitel hatékonysága maximális. E frekvenciaértéktől távolodva (mely a rugóállandóval nő) az átvitel hatékonysága rohamosan csökken. Ezek az eredmények könnyen értelmezhetők. Lassan változó gerjesztés esetén a filamentum-rendszernek van ideje átrendeződni, ezáltal a lehetséges legalacsonyabb energiájú állapotban maradni. Így minimális energiát juttat el a kilépési pontokhoz. Nagy frekvenciák esetén a rendszer nem képes követni a változásokat. Merev testként viselkedik, mely szintén nem jó energiatovábbító médium. Az aktin-filamentumokat összecsatoló tipikus molekulák (mint filamin,
(
m frekvencia, melynél az átvitel hatékonysága maximális. E frekvenciaértéktől távolodva (mely a rugóállandóval nő) az átvitel hatékonysága rohamosan csökken. Ezek az eredmények könnyen értelmezhetők. Lassan változó gerjesztés esetén a filamentum-rendszernek van ideje átrendeződni, ezáltal a lehetséges legalacsonyabb energiájú állapotban maradni. Így minimális energiát juttat el a kilépési pontokhoz. Nagy frekvenciák esetén a rendszer nem képes követni a változásokat. Merev testként viselkedik, mely szintén nem jó energiatovábbító médium. Az aktin-filamentumokat összecsatoló tipikus molekulák (mint filamin,
( -aktinin) effektív rugóállandói a 100-1000 pN/mikron tartományban vannak. Mint az ábráról leolvasható, az átviteli tényező ilyenkor a 10 rad/s körül éri el a maximumot. A gyakorlatban, illetve kísérletekben megvalósuló vagy alkalmazott periodikus perturbációk is legtöbbször ebbe a tartományba esnek
[19, 20].
-aktinin) effektív rugóállandói a 100-1000 pN/mikron tartományban vannak. Mint az ábráról leolvasható, az átviteli tényező ilyenkor a 10 rad/s körül éri el a maximumot. A gyakorlatban, illetve kísérletekben megvalósuló vagy alkalmazott periodikus perturbációk is legtöbbször ebbe a tartományba esnek
[19, 20].
Sajátfrekvenciák és biológiai specificitás. Tudjuk, hogy minden rugalmas rendszer rendelkezik sajátfrekvenciákkal (normálmódusokkal), melyek annak fizikai tulajdonságaitól függnek. Ha egy ilyen rendszert valamely saját frekvenciához közeli frekvenciával gerjesztünk, maximális választ kapunk. Egyetlen ideális rugó sajátfrekvenciája a rugóállandó négyzetgyökével arányos (lásd fentebb  m-nek a rugóállandótól való függését), míg véletlenszerűen elhelyezkedő csatolt rugórendszer (amilyen modellcitoszkeletonunk) esetén a normálmódusok meghatározása általában csak bonyolult numerikus eljárással oldható meg. Az
5. ábra alapján azt a következtetést vonhatnánk le, hogy amennyiben citoszkeletonunkban a rugóállandót a 100-1000 pN/mikron tartományból választjuk, rendszerünk normálmódusainak sűrűsége a fent definiált
m-nek a rugóállandótól való függését), míg véletlenszerűen elhelyezkedő csatolt rugórendszer (amilyen modellcitoszkeletonunk) esetén a normálmódusok meghatározása általában csak bonyolult numerikus eljárással oldható meg. Az
5. ábra alapján azt a következtetést vonhatnánk le, hogy amennyiben citoszkeletonunkban a rugóállandót a 100-1000 pN/mikron tartományból választjuk, rendszerünk normálmódusainak sűrűsége a fent definiált 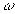 m környékén számottevő.
m környékén számottevő.
A 6. ábra modell-citoszkeletonunk sajátfrekvenciaspektrumát mutatja. Ezt a spektrumot a következőképpen kaptuk. Ha egy rugalmas elemeket tartalmazó csatolt rendszer rezeg, annak minden komponensének rezgése kifejezhető a normálmódusok lineárkombinációjaként, így e rendszerből tetszőlegesen kiválasztott rugó l hosszának időbeli változását az
![]()
kifejezés adja meg. Itt 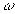 i az i-edik normálmódus frekvenciája, ai annak relatív amplitúdója, az összegzést i lehetséges értékeire kell elvégezni. Követtők tehát egy adott rugó mozgását, majd a hosszának időbeli megváltozását leíró görbét Fourier-transzformáltuk. Az így kapott függvény négyzetét (amit nem normált teljesítményspektrumnak nevezőnk) mértük fel a
6. ábra függőleges tengelyére. A számítást k = 100 pN/mikron és
i az i-edik normálmódus frekvenciája, ai annak relatív amplitúdója, az összegzést i lehetséges értékeire kell elvégezni. Követtők tehát egy adott rugó mozgását, majd a hosszának időbeli megváltozását leíró görbét Fourier-transzformáltuk. Az így kapott függvény négyzetét (amit nem normált teljesítményspektrumnak nevezőnk) mértük fel a
6. ábra függőleges tengelyére. A számítást k = 100 pN/mikron és
 = 10
= 10 v értékekre végeztük el, a gerjesztőferkvenciát 50 rad/s-nak választottuk. Az 5.
és 6. ábra összehasonlításából látszik, hogy a rendszernek
v értékekre végeztük el, a gerjesztőferkvenciát 50 rad/s-nak választottuk. Az 5.
és 6. ábra összehasonlításából látszik, hogy a rendszernek 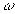 m közelében számos sajátfrekvenciája van.
m közelében számos sajátfrekvenciája van.
A sejtciklus során a sejt citoszkeletonja többször átrendeződik. Jelentős strukturális változások következnek be, ha a sejt mozog, valamint amikor beindul a sejtosztódás. Ezek a folyamatok egyúttal biológiailag specifikus utasításokat, jeleket igényelnek. Az alaki változások során a filamentum-rendszer sajátfrekvencia-spektruma is módosul, ami befolyásolja, hogy milyen frekvenciájú külső jel jut hatékonyan rendeltetési helyére. Ily módon tehát a sejt fizikai tulajdonságait felhasználhatja biológiai specificitás eléréséhez.
Összefoglalás
Az intracelluláris jelvezetés két, fizikai mechanizmusokon alapuló lehetőségét mutattunk be. Mindkét modell alapvető feltevése, hogy a sejt alakját is nagyban meghatározó citoszkeleton egy a perkolációs küszöb felett lévő összefüggő rendezetlen filamentum-rendszert képez. Egy ilyen rendszer képes mind biokémiai, mind pedig mechanikai jeleket továbbítani. Az első lehetőséget egy jelzőmolekulának a filamentum-rendszer mentén történő véletlen bolyongásával mutattuk meg. Ez a modell egyben a lehető legegyszerűbb jeltovábbító pályának felel meg. Láttuk, hogy egy ilyen mechanizmus segítségével a biokémiai jel sokkal megbízhatóbban és gyorsabban jut tatható rendeltetési helyére, mint a viszkózus és organellumokkal teli citoplazmában történő diffúzió útján. A filamentum-rendszer mentén történő mozgás nagy előnye, hogy a diffúziót akadályozó organellumok kikerülhetők. Vajon mi tarthat egy molekulát a filamentum közelében? Egy lehetőség az elektrosztatikus kölcsönhatás. Ismert, hogy az aktin-filamentumok, és a mikrotubulusok is negatív töltésűek. Ugyanakkor a jelvezető molekulák tipikusan fehérjék. Mint ilyenek tartalmaznak mind negatív, mind pozitív töltésű aminosavakat. A bonyolult struktúrájú fehérjék lokális töltéseloszlása elvben tehát lehetővé teszi a szükséges vonzó kölcsönhatás létrejöttét.
A mechanikai jeltovábbítás lehetőségét úgy mutattuk meg, hogy mechanikai energiát juttattunk a citoszkeletonba, majd a filamentum-rendszer és a citoplazma néhány fizikai tulajdonságának függvényében kiszámítottuk az energiaátvitel hatékonyságát. A sejten belül terjedő mechanikai jelnek két alapvető nehézséggel kell szembenéznie. Egyik az energiadisszipáció, a másik a biológiai specificitás követelményéből adódik. A citoplazma viszkozitása azt eredményezheti, hogy a jel továbbításához szükséges energia annyira lecsökken, hogy a jel elvész a háttérzajban. Eredményeink azt mutatják, hogy a citoszkeleton segítségével a jel viszonylag gyorsan képes végighaladni a sejtfal és a sejtmag közötti térrészen anélkül, hogy amplitúdója a felismerhetetlenségig lecsökkenne. Továbbá a jelet reprezentáló mechanikai hullám frekvenciája a filamentum-rendszer normálmódusaihoz hangolható, amivel a biológiai specificitás biztosítható.
Az ismertetett eredményekből levonható legfontosabb konklúzió, hogy a citoszkeleton a sejt szignalizációs apparátusának lényeges része lehet. Segítségével gyorsan és megbízhatóan továbbítható információ a sejtfaltól a sejt különböző részeibe (többek között a sejtmagba). Mivel a citoszkeleton a sejt belsejét teljesen átszövő csatolt rendszer, valamint kontrollálja a jelvezetésben aktív szerepet játszó molekulák térbeli elhelyezkedését, ezért ideálisan alkalmas biokémiai és mechanikai jelek szintetizálására.
____________________________________
1 Lásd a megfelelő ábrákat a 4. számú Hivatkozásban.
2 Az olvasó a perkoláció elméletének és alkalmazásainak részletes tárgyalását megtalálja Sahirni könyvében [10].
3 A matematikai részleteket az olvasó megtalálja a 14. hivatkozásban.
4 Megjegyezzük, hogy egy diszkrét filamentum-rendszer mentén számított EAI nem lehet kisebb, mint annak fenti értelemben vett ekvivalens folytonos térre vonatkozó értéke. A 14. hivatkozásban megmutattuk, hogy ama feltevéstank miszerint a háromdimenziós és egydimenziós diffúziós állandók megegyezhetnek, realisztikusan teljesülhet a sejten belül fennálló feltételek mellett. Egydimenziós diffúziós állandót használunk amikor a molekula bolyongását filamentum mentén vizsgáljuk. végül, folytonos térbeli diffúzióra vonatkozó számításainkat úgy végeztük, hogy megoldottuk a megfelelő Dynkin-egyenletet [15] a sejtmag és a sajtfal között kifeszített nagyon kis rácsállandójú rácson.
5 Az integrinek a sejtfelületen elhelyezkedő speciális fehérjék, melyek a sejt és a sejtközi állomány összetevői között létesítenek adhéziót.