Nagy Károly
ELTE Elméleti Fizikai Tanszéke

A Magyar Tudományos Akadémia és az Eötvös Loránd Tudományegyetem által rendezett emlékülésen olyan tudósra emlékezünk ma, akinek - Planckkal, Einsteinnel, Bohrral és Dirac-kal együtt - a legnagyobb hatása volt a világról alkotott mai természettudományos képünk kialakulására. Ő ismerte fel először, hogy a mikrovilág kvantumos sajátságainak az értelmezéséhez az eddig használt folytonos függvények helyett olyan matematikai szimbólumokat kell alkalmaznunk a kinematikai és dinamikai mennyiségek reprezentálására, amelyek általában nem cserélhetők fel egymással. Róluk később kiderült, hogy a mátrixok algebrai szabályait követik, és diszkrét sajátértékekkel rendelkeznek. Ez a felismerés olyan merészen új volt, hogy még a legközvetlenebb munkatársaiban is meghökkenést váltott ki.

Azt a negyed századot akarom bemutatni, amelyik a kvantummechanikát megelőzte, és tulajdonképpen előkészítette. Ennek a kornak a hangulatát szeretném érzékeltetni, ami jellemezte a fizikus közösséget, elsősorban Európában és annak is néhány rangos egyetemén. E vonatkozásban kiemelést érdemel Berlin, Göttingen, Koppenhága és München. Ezeken az egyetemeken dolgoztak a kor kiemelkedő tudósai, akiknek meghatározó szerepük volt a huszadik század fizikájának megalapozásában.

A kvantummechanikához vezető negyed század fizikai felismeréseinek sora a hőmérsékleti sugárzásra vonatkozó Planck-törvénnyel kezdődik. Ennek százéves jubileumáról a múlt esztendőben emlékeztünk meg. Ezért ezt most nem részletezem, csupán megemlítem, hogy egy tükröző Falakkal bezárt térrészben kialakult, termodinamikai egyensúlyban lévő elektromágneses sugárzás energia-sűrűségének a hőmérséklettől és a frekvenciától való függését Planck azzal a klasszikus fizikától teljesen idegen feltevéssel tudta a tapasztalattal egyezően megmagyarázni, hogy a sugárzást kibocsátó testnek gondolt oszcillátor energiáját hv kvantumok egészszámú többszörösének tekintette. Következésképpen ezek az oszcillátorok a sugárzást hv kvantumok formájában bocsátják ki és nyelik el. Ez a feltevés a klasszikus fizika fogalomvilágához szokott fizikusok körében szinte istenkáromlásként hatott. Elég hosszú ideig Planck is csak munkahipotézisnek tekintette, úgy gondolta, hogy a valóságos folyamatokban az energia természetesen folytonosan változik, ahogy azt a klasszikus fizika tanítja. Planck nagyobb jelentőséget tulajdonított a h hatáskvantumnak. Tudományos életrajzában erre így emlékezik vissza. “Amikor a hatáskvantum jelentését entrópia és valószínűség kapcsolatára végérvényesen megállapítottam, még teljesen megmagyarázatlan maradt az a kérdés, hogy milyen szerepet játszik a h állandó a fizikai folyamatok töményszerű lefolyásánál. Ezért rövidesen elkezdtem próbálkozni, hogy a hatáskvantumot valamiképpen beillesszem a klasszikus elmélet kereteibe, de a hatáskvantum minden ilyen kísérletnek makacsul ellenszegült. ... Miután minden kísérlet meghiúsult, nem volt többé kétség aziránt, hogy a hatáskvantum alapvető szerepet játszik az atomfizikában, és hogy fellépésével új korszak kezdődik a fizikában. A hatáskvantumban ugyanis valami eddig soha nem hallott jelentkezik, amely arra van hívatva, hogy alapjában átalakítsa egész fizikai gondolkodásunkat, amely azóta, hogy Leibnitz és Newton megalapozta az infinitezimális számítást, minden kauzális összefüggés folytonosságának feltételezésén alapult. Hiábavaló kísérleteim, hogy a hatáskvantumot valamiképpen belehelyezzem a klasszikus elméletbe, több éven át elhúzódtak, és igen sok munkámba kerültek... Most tehát pontosan tudtam, hogy a hatáskvantum a fizikában jelentősebb, mint ahogy kezdetben hajlamos voltam, feltételezni, és teljesen átértettem, mennyire szükséges, hogy teljesen új szemléletet és számítási módszert vezessünk be atomisztikus problémák tárgyalásánál. "

A kvantumhipotézis fizikai jelentőségét, vagyis, hogy az energia kvantumos szerkezetű, Einstein ismerte fel. Ennek alapján adott magyarázatot 1905-ben a fényelektromos jelenségre, amelyet a fény hullámelmélete alapján nem lehetett megérteni. Itt arról van szó, hogy ha fémlemezt - különösen alkálifémet - ultraibolya fénnyel megvilágítunk, elektronok lépnek ki a fém felületéből. A tapasztalat azt mutatta, hogy a kirepülő elektronok sebessége nem függ a megvilágító fény intenzitásától, hanem csak a frekvenciájától. A frekvencia növelésével nő az elektronok sebessége. Másrészt a kilépő elektronok száma a fény intenzitásától függ. Einstein magyarázata szerint a fém felületén levő atom a beeső fényből elnyel egy energiakvantumot, ezáltal egy elektronja akkora energiát vesz fel, hogy kiszakad az atom kötelékéből. A fémre eső fénykvantum hv energiája fedezi a kilépéshez szükséges munkát és az elektron mozgási energiáját a hv = mv²/2 + A képlet szerint. (m az elektron tömegét, v a sebességét, A pedig a kilépési munkát jelenti.) Mivel a tankönyvek nem nagyon közlik Einstein gondolatmenetét, amely őt a fény korpuszkuláris felfogásához vezették, ezért röviden vázolom. Gondoljunk el egy teljesen tükröző falakkal bezárt V térfogatú üreget, amelyet v frekvenciájú monokromatikus sugárzás tölt ki. Egyensúlyi állapotban a sugárzás energiája egyenletesen oszlik el az egész térfogatban, de a statisztikus ingadozások miatt bekövetkezhet az az eset is, amikor az egész E energia egy V₁ résztérfogatban egyesül. Ennek valószínűsége Einstein számítása szerint (V₁/V)^E/hv Ez a képlet nagyon hasonló ahhoz, amelyik megadja, hogy az N atomból álló ideális gáz milyen valószínűséggel lesz a V térfogat V₁ részében: (V₁/V)^N. A két kifejezés egybevetéséből látszik, hogy az E/hv ugyanolyan szerepet játszik, mint a gázatomok N száma. Ebből arra a következtetésre jutott, hogy a fény felfogható úgy, mintha energiája hv nagyságú kvantumokból állna. Az E/hv mennyiség a fénykvantumok számát jelenti. A gázatomokkal való hasonlóságot Einstein tovább vitte a fényt az ideális gázhoz hasonlóan részecskék összességének tekintette. Feltevése szerint a fényrészecskéknek (amelyeket később fotonoknak neveztek el) nemcsak hv energiájuk, hanem hv/c impulzusuk is van. Ez a foton impulzus ugyanolyan alakba írható, mint a közönséges részecske impulzusa, nevezetesen, tömeg x sebesség szorzat alakjában. Mivel c sebességgel mozog, a hv/c impulzus kifejezésből a foton tömegére hv/c² adódik. Ez a foton tehetetlen tömege. Nyugalmi tömege természetesen zérus. Ez a gondolatsor az elektrodinamika Maxwell-elméletével teljesen ellentétben áll, mert az a fényt folytonos hullámként írja le, és a tapasztalattal tejes egyezésben magyarázza a visszaverődés, törés, interferencia és elhajlás jelenségét. Tulajdonképpen már a hőmérsékleti sugárzás problémájánál a fény kvantumos szerkezetével találkozunk. Hiszen ha a fényforrásként tekintett oszcillátor a sugárzást hv adagokban bocsátja ki és nyeli el, akkor ebből természetes módon adódna a következtetés, hogy a fényenergia kvantumos szerkezetű. Planck azonban oly mértékben meg volt győződve a Maxwell-elmélet igazáról, hogy ettől a lépéstől visszariadt. Einstein egész alkotói tevékenységét viszont az jellemzi, hogy mentes az előítéletektől. A fényelektromos jelenségben meg is találta elképzelésének tapasztalati megerősítését. A sugárzás részecske-tulajdonságainak meggyőző kísérleti bizonyítéka a Compton által 1923-ban elvégzett szórás kísérlet, a Compton-szórás. Itt arról van szó, hogy elektromágneses sugárzás, például röntgensugár szóródik könnyű elemekből álló anyagon, és közben megváltozik a szórt sugárzás frekvenciája a beesőéhez képest. Ugyanekkor a könnyű elemből elektronok repülnek ki. A jelenség egyszerűen és szemléletesen magyarázható a fény részecske-jellege alapján. A beeső foton (mint részecske) az atom elektronjával ütközik, ekkor energiájának egy részét átadja az elektronnak. Nagy frekvenciájú fény esetén az elektron kötési energiája elhanyagolható a foton energiája mellett, és így a jelenség úgy fogható fel, mintha a foton szabad elektronon szóródna. Az energia- és impulzus-tételből kiszámítható a fény frekvenciaváltozása, amely jól egyezik a kísérleti eredményekkel.

Az elektromágneses sugárzásra vonatkozó Einstein-féle hipotézis, miszerint a fény energiája és impulzusa fényrészecskék (fotonok) energiájából és impulzusaiból tevődik össze, tehát maga a sugárzás kvantumos szerkezetű, a huszadik század első két évtizedében igen élénk vitáknak volt a tárgya. Az értelmezésnél az okozta a nagy gondot, hogy (miként fentebb említettük) sok jelenségben a fény úgy viselkedik, mintha hullám lenne. Külön érdekessége a dolognak, hogy a részecske-tulajdonságokat megtestesítő foton energiájának és impulzusának kifejezése a Planck-állandónak és a hullámfogalomhoz tapadó frekvenciának, illetve reciprok hullámhossznak a szorzata. Tehát a részecske-kép is használja a hullámfelfogás egyes paramétereit. A sugárzásnak ez a kettős részecske-hullám-természete volt a fő témája az 1911-ben Brüsszelben megtartott első Solvay-konferenciának. Ez a konferencia sorozat (a háborús éveket kivéve) néhány évtízedik tartott, és az éppen aktuális kérdések megvitatását tűzte ki célul. Ernest Solvay belga fiziko-kémikus indította útjára és halála után az ugyancsak általa alapított Nemzetközi Fizikai Intézet szervezte őket tovább. Fizikatörténeti szempontból rendkívüliek ezek a konferenciák, mert hűen tükrözik a kor fizikájának legizgalmasabb kérdéseit és a hozzájuk kapcsolódó vitákat, az írj fogalmak térhódítását, és a kialakulóban lévő kvantumelmélet értelmezésének letisztulását. Meg kell említeni; hogy a kezdeti időszakban ezeknek a vitáknak elsősorban Albert Einstein és Niels Bohr voltak a főszereplői, de később ott voltak az akkor még egészen fiatal Heisenberg, Pauli és Dirac is, akik a fizika fogalomrendszerének radikális megváltozását kezdeményezték.

Heisenberg határozottan képviselte azt a nézetet, hogy az atomok fizikájának a megfogalmazásában csak megfigyelhető mennyiségekhez kapcsolódó fogalmak szerepelhetnek. Például az elektron pályája az atomban nem figyelhető meg, ezért az elméleti leírásból is ki kell küszöbölni. Ez nem megy könnyen, mert a megszokott, eddig jól bevált régi fogalmaktól nehéz megszabadulni. Ez még inkább igaz, ha az atomfizikai jelenségekhez a makroszkopikus világból vett képeket társítjuk. Érdemes itt megemlíteni, hogy Heisenberg egyik előadása után Berlinben Einstein megkérdezte tőle, hogy honnan veszi ezt a filozófiát, hogy csak megfigyelhető mennyiségeket szabad használni az új elmélet megfogalmazásában. Heisenberg azt válaszolta, hogy Einsteintől, aki ugyanezt tette a relativitáselmélet megalkotásakor. Erre Einstein azt felelte, hogy az lehet, de akkor is nonszensz, mert mindig az elmélet mondja meg, hogy mit lehet és kell megfigyelni. Még egy rövid megjegyzés erejéig visszatérve a fény kettős természetéhez, megemlítem, hogy a kvantummechanika szerint az eredetileg részecskének gondolt objektumoknak is megvan ez a kettős természete. Itt csak utalok a Davisson-Germer elektron-szórási kísérletre. A megfigyelés jellegétől függően egyik vagy a másik kép jelenik meg. Ezek a képek egy időben egymást kizárják; de egymást kiegészítve adnak teljes képet a megfigyelt objektumról vagy jelenségről. A Bohr-féle komplementaritási elvnek ez éppen a lényeges eleme. Ennek részleteibe itt nem megyek bele.

Visszatérve az elektromágneses sugárzás problémájához még megemlítem, hogy Einstein később is igen behatóan foglalkozott vele. A sugárzásra vonatkozó Planck-törvénnyel kapcsolatban az izgatta, hogy milyen e sugárzás valódi mechanizmusa. A sugárforrásként szolgáló oszcillátor energiája kvantált. A két szomszédos energiaszint különbsége hv. Gondoljuk el, hogy N₁ számú oszcillátor van az E₁, és N₂ számú az E₂ energiájú állapotban. Tegyük fel, hogy E₁ > E₂. Elvben valamennyi E₁ energiájú oszcillátor átmehet az alacsonyabb energiájú állapotba hv energiájú foton kibocsátásával. A valóságban nem ez következik be, hanem adott idő alatt az oszcillátoroknak csak egy része vesz részt az átmenetben. Ezért Einstein bevezette az átmeneti valószínűség fogalmát, amely megadja azon oszcillátoroknak a hányadát, amelyek időegység alatt az alacsonyabb energiájú állapotba mennek. Nyilvánvaló, hogy az átmenetben résztvevő oszcillátorok száma az átmeneti valószínűségnek az N₁-gyel való szorzata lesz. A sugárzás hatására az alacsonyabb energiájú oszcillátorok egy része foton elnyelésével magasabb energiájú állapotba gerjesztődik. Ebben a fordított folyamatban résztvevő oszcillátorok száma arányos lesz N₂-vel, a sugárzás energiasűrűségével és az átmenet valószínűségével. Első pillanatban azt gondolnánk, hogy az egyensúly feltétele e két szám egyenlősége. Ez azonban nem vezet a Planck-törvényre. Einstein felismerte, hogy egy harmadik folyamat is van, nevezetesen, a sugárzás hatására bekövetkező indukált emisszió. Az egyensúly feltétele tehát az, hogy e kétfajta emisszióban időegység alatt átlagosan résztvevő oszcillátorok száma egyezzen meg az abszorpcióban résztvevők számával. Ez a feltétel igen egyszerűen vezet a Planck-törvényhez, ha feltesszük, hogy az indukált emisszió és az indukált abszorpció átmeneti valószínűségei egymással megegyeznek, valamint az N₁ és N₂ számokat a Boltzmann-statisztika alapján számítjuk. Fizikai tartalmát tekintve a Planck-törvénynek ez a levezetése a leggazdagabb. Az átmeneti valószínűség fogalmának a bevezetésével Einstein a sugárzás mechanizmusának a leglényegesebb kvantumfizikai törvényszerűségét ismerte fel. A később kidolgozott kvantummechanika és a kvantumtérelmélet ma is ennek a fogalomnak a felhasználásával írja le az átmeneteket a kvantumállapotok között. A kvantummechanika állapotfüggvényének Max Borntól származó értelmezése is a valószínűség fogalmán alapszik. Minőmáig rejtélye a fizikatörténetnek számomra, hogy Einstein, aki elsőként vezette be a valószínűség fogalmát a kvantumelméletbe, annak statisztikus értelmezésével élete végéig nem tudott egyetérteni. Fizikus körökben közismert a mondása, nem hiszi, hogy az Úristen kockajátékos lett volna, amikor a világot teremtette.

Napjaink fizikai aktualitása miatt mindenképpen meg kell említeni az indiai származású Bose nevét, aki a sugárzást Einstein nyomán foton-gáznak tekintette, és feltette, hogy a fotonok nem különböztethetők meg egymástól.

(A fénykvantumok megkülönböztethetetlenségét először 1911-ben Natanson lengyel fizikus állította.) Ezek alapján a statisztikus mechanika módszereivel a legegyszerűbben jutott a Planck-törvényhez. Dolgozatát még a közlés előtt elküldte Einsteinnek, aki Bose módszerét ideális gázra alkalmazta, ennek során jött rá a Bose-Einstein-kondenzáció néven ismert kvantumfizikai jelenségre. Ennek lényege, hogy egy bizonyos kritikus hőmérséklet alá hűtve a gázt, a gázmolekulák egy bizonyos hányada a kvantummechanikai alapállapotba kerül. Ez az alapállapotban lévő gázmolekulák összessége a Bose-Einstein-kondenzátum. Ennek kísérleti kimutatását jutalmazták az idén fizikai Nobel-díjjal.

A tizenkilencedik század végén a megoldatlan fizikai problémák között szerepelt a szilárd anyagok fajhőjének viselkedése az abszolút zéruspont közelében. A Boltzmann-statisztika szerint a szilárd anyagok fajhője a hőmérséklettől független állandó. A Nernst által 1906-ban felfedezett, a termodinamika harmadik főtétele szerint viszont zérushoz kell tartania, amint a hőmérsékletet közelítjük a zérus pont felé. Az ellentmondás feloldásához is Einstein adott útmutatást. A szilárd anyag atomjai az egyensúlyi helyzet körül harmonikus rezgéseket végeznek. Az atomokat tehát felfoghatjuk, mintha oszcillátorok lennének. Az oszcillátor energiájáról pedig már a kvantumhipotézis óta tudjuk, hogy csak kvantált értéket vehet fel. Ennek alapján az atom energiája kvantált oszcillátorenergiák középértéke. Az egyszerű számítás olyan fajhőkifejezésre vezet, amely tartalmazza a hőmérsékletet, és ha a hőmérséklettel a zérusponthoz közeledünk, a fajhő is tart zérushoz. Ezt a gondolatot fejlesztette tovább Debye azzal a finomítással, hogy az atomokat nem monokromatikus oszcillátorokkal helyettesítette, hanem figyelembe vette a kristályrácsnak, mint egésznek a kollektív rezgéseit, amelyek során különböző sajátfrekvenciákat kapunk. Így a tapasztalattal jól egyező hőmérsékletfüggést kapott. A fajhő T³ szerint tart a zérushoz, midőn a hőmérséklet a zérusponthoz közeledik. A lényeg meglátása azonban itt is Einstein érdeme.

A sugárzásokra vonatkozó új megismerésekről áttérve a vizsgált kor fizikai fejlődésének másik vonulatára, az anyag szerkezetét érintő fontosabb felfedezésekről akarok még szólni.

A radioaktivitás és az elektron felfedezésével kísérlettel is igazolttá vált az anyag korpuszkuláris felépítésére vonatkozó hipotézis, amely a 19. században a kinetikus gázelmélet alapját képezte. Az anyagból elektronok és alfarészek jönnek ki. Természetes volt tehát a gondolat a tizenkilencedik és a huszadik század fordulóján, hogy az atomnak van valamilyen szerkezete. Az elektront felfedező J.J. Thomsonnak az volt az elképzelése, hogy az atomban a pozitív elektromos töltés folytonosan oszlik el az atom gömbszerűnek képzelt egész térfogatában, és ebben annyi elektron helyezkedik el, hogy az atom kívülről elektromosan semleges legyen. Volt olyan elképzelés, hogy több ezer elektronról van szó. Ennek az elképzelésnek ellentmondtak Lénárd kísérletei, aki elektronokkal bombázta az anyag atomjait, és azt tapasztalta, hogy sok elektron eltérítés nélkül halad tovább. A pozitív töltés tehát nem töltheti ki az egész térfogatot, mert akkor az elektromos kölcsönhatás miatt az elektronok eltérülnének. Lénárd ezekből arra következetett, hogy az atomban a pozitív töltés néhány pontban koncentrálódik, ezek körül helyezkednek el a negatív elektronok. Rutherford ezzel szemben úgy gondolta, hogy az atom pozitív töltése egyetlen kis központi tartományban sűrűsödik össze, és ezt veszik körül az elektronok. Ő nevezte el az atom kis központi pozitív töltésű részét az atom magjának. Elgondolását 1909-től kezdve kíséreltekkel is megalapozta. Rádium-C sugárforrásból származó alfa-részeket keskeny sugárban valamely anyag vékony lemezére bocsátotta, és vizsgálta azok eltérülését. Az atom magja és az alfa-rész között Coulomb-kölcsönhatást feltételezve, elméleti úton kiszámítható a szórt alfa-részek eloszlása, és ezt ellenőrizhetjük a kísérletek eredményével. A kísérletek azt mutatták. hogy 90 foknál nagyobb szögben is térülnek el alfa-részek. Az elméleti képletekkel összevetve arra lehetett következtetni, hogy az alfa-részek 10^-12 cm távolságra megközelítik az atom magját, és itt még a számításnál teltételezett Coulomb-erő hat. A magon belül más természetű erők is hatnak, de a kísérlet tanúsága szerint ilyen távolságban ezek még nem jelentősek. Rutherford ebből arra következtetett, hogy az atom magja igen kis tartományra, 10^-12 cm-nél kisebb sugarú gömbre koncentrálódik. A pozitív töltésű mag körül mozognak valahogyan az elektronok. A legegyszerűbb elképzelés szerint körpályákon. Ezzel a modellel azonban baj van, mert az elektrodinamika szerint a körpályán mozgó elektromos töltésnek sugároznia kell. Ha sugároz, akkor veszít az energiájából, és egyre kisebb sugarú pályára kerülve, végül a teljes energiáját elveszítve belezuhan a magba. A Rutherford-modell tehát nem stabil. A mindennapi tapasztalat nem ezt mutatja, mert a környező világ és benne mi is létezünk, atomjaink nem omlanak össze.

A Rutherford-modell nehézségeinek kiküszöbölésére Niels Bohr a következő feltevésekkel módosította a modellt:

1. Az elektronok körpályákon mozognak az atomban, de a klasszikus mechanika szerint lehetséges pályák közül csak olyanokon, amelyeken az elektronnak a magra vonatkoztatott impulzusnyomatéka a Planck-állandó 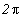-ed részének egész számú többszöröse. Bohr eredetileg e helyett azt a feltételt szabta ki, hogy az elektron mozgási energiájának a kétszerese legyen egyenlő a hv energia kvantum egész számú többszörösével. Tehát legyen 2E_{k =} nhv. Könnyű belátni, hogy körpálya esetén ez megegyezik az impulzusnyomatékra kimondott feltétellel.

2. Az így kiválasztott stacionárius pályákon keringő elektron nem sugároz. Sugárzás akkor lép fel, amikor az elektron egy magasabb energiájú stacionárius pályáról alacsonyabb energiájúra ugrik.

3. A két állapot közötti átmenet során kibocsátott sugárzás frekvenciáját a két energia különbsége határozza meg az E₂ - E₁ = hv képlet szerint. E három feltételre alapozott kvantumelméletet nevezzük Bohr-elméletnek. A hidrogénatomra egyszerű számítással meghatározhatók a stacionárius állapotok energia értékei, a megfelelő pályák sugarai, valamint a megengedett átmenetek során kibocsátott sugárzás frekvenciái. A hidrogénatom diszkrét energia értékeire olyan kifejezés adódik, amely az 1. feltételben szereplő egész szám (kvantumszám) négyzetét tartalmazza a nevezőben. A 3. feltétel alapján számított frekvenciák a hidrogén vonalas színképének elméleti értelmezését adják. A korábban empirikus úton megállapított Balmer- és egyéb sorozatok egy csapásra magyarázatot nyertek. A színképvonalak káoszában a Bohr-elmélet rendet teremtett. Ez volt az elmélet első szép sikere. Érdemes megjegyezni, hogy Bohr volt az, aki először tételezte fel, hogy a hidrogénatomban csak egy elektron van, amelyik körpályán kering az egységnyi pozitív töltésű mag körül.

A hidrogénatomra vonatkozó számítás általánosítható azokra az esetekre is, amikor nehezebb atomokról van szó, de csak egyetlen elektron kering a külső pályán, a többi zárt héjat alkotva, részben leárnyékolja a mag vonzó hatását. Ezek a számítások kvalitatívan a nehezebb elemeknél is számot adnak az energiaszintek diszkrét sorozatáról. A számszerű tényezőben mutatkozó kisebb pontatlanságok a leárnyékolás közelítő jellegű figyelembe vétele miatt lépnek fel. Az 1913-ban elvégzett Franck-Hertz-kísérlet az atomok energiaszintjeinek diszkrét voltát igazolja. Az atomokon szóródó elektronok csak akkor tudnak energiát átadni az atomnak, ha energiájuk megegyezik két energiaszint különbségével. Ilyenkor a rugalmatlanul ütköző elektron elveszíti mozgási energiáját, emiatt leesik a kísérlet során mért anódáram. Az így gerjesztett állapotból az atom alacsonyabb energiájú állapot a jut egy foton kibocsátásával. A kísérletben megfigyelt sugárzás frekvenciája megfelel a Bohr-féle frekvencia feltételnek.

A hidrogénatom vonalas színképének finomszerkezetéről az elmélet eredeti Bohr-féle megfogalmazása nem ad számot. Az elméletet Arnold Sommerfeld általánosította ellipszis-pályákra, és figyelembe vette a relativisztikus mechanika törvényeit is. Az első kvantumfeltétel helyére most három lép, annak megfelelően, hogy az ellipszispálya alakját és térbeli elhelyezkedését a három (r, q , j ) gömbi koordinátával adhatjuk meg. A második kvantumfeltétel azt fejezi ki, hogy az impulzusnyomaték a Planck-állandó 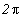-ed részének egész számú többszöröse, a harmadik pedig az impulzusnyomaték z-komponensére mondja ugyanezt. Az ellipszispályák a térben tehát nem tetszőlegesen helyezkedetek el, hanem úgy, hogy az impulzusnyomatéknak a z-tengelyre vonatkozó vetülete a h/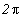-nek egész számú többszöröse. Ennek megfelelően a Sommerfeld-féle általánosításban három kvantumszám jelenik meg, az elektron energiájának kifejezése mind a hármat tartalmazza. Ez eredményezi az energiaszintek felhasadását és a színképvonalak finomszerkezetét.

Az impulzusnyomaték nagyságának és irányának kvantáltsága egyúttal az atom mágneses nyomatékára is vonatkozik, mert a mágneses nyomaték az impulzusnyomatékkal arányos. Azt, hogy az atom mágneses nyomatéka külső mágneses térhez képest csak meghatározott irányokba állhat be, Stern és Gerlach 1922-ben kísérlettel igazolták. Ugyancsak a mágneses nyomaték kvantáltságával magyarázható meg a Zeeman-effektus is. E szerint az atom színképvonalai mágneses térben felhasadnak. Ez az atom mágneses nyomatékának a mágneses térrel való kölcsönhatásából származó energia kvantáltságának a következménye. A Zeeman-effektus tanulmányozása fontos szerepet kapott a kvantumelmélet kialakulásában. Heisenberg is ezt kapta első feladatul Sommerfeldtől. A vizsgált kísérleti spektrumot nagy meglepetésére feles kvantumszámokkal tudta csak értelmezni. Az eredményt Sommerfeld sem fogadta el, mert ekkor még a spin-kvantumszám ismeretlen volt. A spint Goudsmit és Uhlenbeck 1924 végén fedezték fel.

A Bohr-Sommerfeld-féle kvantumelmélet sok szép sikere ellenére nem volt tökéletes. A héliumatomot már nem lehetett vele eredményesen tárgyalni. Sommerfeldnek és tanítványainak minden próbálkozása sikertelen maradt. A hidrogénatomnál is csak a színképvonalak frekvenciáit adta meg jól, azok intenzitását már nem. Az impulzusnyomaték kvantált értékeit is hibásan adta, ugyanis a h/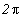 szorzójaként a mellékkvantumszám szerepel. A helyes érték - miként az a kvantummechanikából kiderült - [l(l+1)]^1/2 h/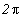. Mégis azt kell mondanunk, hogy a Bohr-elmélet abból a szempontból sikeres volt, hogy a klasszikus fizika fogalomvilágához képest teljesen új gondolkodást hozott a fizikába. A kortársalt egy része kezdetben nem hitt benne. Olyan kiváló fizikusok is, mint Laue és Stern a cikk megjelenése után közvetlenül olyan őrült ötletnek tartották, hogy ha igaznak bizonyul, akkor otthagyják a fizikát. Kiderült, hogy mégsem volt őrült ötlet, és nem hagyták ott a fizikát. Sőt, Nobel-díjjal jutalmazott munkával járultak hozzá az atomfizika alakításához. Einstein viszont mindjárt a kezdetén nagyra értékelte. Hevesy György 1913 szeptemberében azt írta Bohrnak, hogy “Ma délután beszéltem Einsteinnel... megkérdeztem őt arról, hogy mi a véleménye az ön elméletéről. ...Azt válaszolta, hogy az nagyon érdekes, ha tényleg jó, és megemlítette, hogy neki nagyon hasonló elgondolása volt több évvel ezelőtt, de nem volt bátorsága annak kifejezésére."

Amikor Hevesy elmondta Einsteinnek Bohr számítását a hélium-ion Rydberg-állandójának a hidrogén-atom Rydberb állandójához való viszonyáról, hogy az a kísérleti értékkel négy tizedes jegyig megegyezik, Einstein azt válaszolta, hogy ez óriási teljesítmény. Rutherford is elismeréssel volt róla mindjárt a kezdetektől.

A Bohr-elméletre vonatkozó ismertetésemet egy anekdotával, és Abraham Pais hozzáfűzött megjegyzésével zárom. Bohr nyaralójának bejárati ajtaja fölött egy patkó volt felszögezve. Egyik vendége (talán éppen Pauli) kicsit meghökkenve kérdezte Bohrtól, elhiszi-e a babonát, hogy ez a lópatkó szerencsét hoz? Bohr azt felelte, hogy természetesen nem, de azt mondják, hogy ha nem hisz valaki benne, akkor is segít. Pais a régi kvantumelméletről, amely a Planck-féle kvantumhipotézissel kezdődött és 1925-ig, a kvantummechanika megszületéséig tartott, úgy nyilatkozott a témakörről szóló történeti írásában, hogy az nagyon hasonlít a bejárati ajtó feletti lópatkóhoz.

A különféle atomfizikai problémáknak a Bohr-elmélet alapján való tárgyalása szinte mindig azt mutatta, hagy a megoldásban van valami helyes eredmény is, de sohasem adott teljesen pontos leírást és magyarázatot. Mivel a hatáskvantum az elméletben a megfelelő helyeken fordul elő, a mikrovilág kvantumos természetét kvalitatíven tükrözi. A hibás válaszok vagy a nem jó eredmények azt mutatják, hogy a klasszikus fizika fogalomvilágának radikálisabb megváltoztatása kell egy új mechanika megalkotásához. Különösen a húszas évek elején Bohr és a koppenhágai Fizikai Intézetben hosszabb-rövidebb időt eltöltő fiatal fizikusok körében jelentek meg leginkább az új, merész gondolatok. Példaként megemlítem, hogy Bohr, Kramers, és Slater a diszperzió tanulmányozásánál még az energia megmaradásának a tételéről is hajlandók voltak lemondani az egyes atomi folyamtokban. Megengedték azt a lehetőséget, hogy ez a fontos fizikai tétel csak statisztikusan lenne érvényes. A fény hullám- és részecske-természetének az összeegyeztetésére irányuló törekvések során vetődött föl ez a gondolat, de csak átmenetileg. Heisenberg is ebbe a diszperzióra vonatkozó kutatásba kapcsolódott be Bohrnál tett első rövidebb tanulmányútja során. Ő volt a legmerészebb a megszokott gondolkodástól való elszakadásban. A bevezető részben már említettem, hogy azt a határozott filozófiát követte, hogy csak megfigyelhető mennyiségek szerepelhetnek az új elméletben. Az elektron pályája az atomban nem ilyen. A diszperzióval való foglalkozás vezette rá, hogy e helyett a helykoordináta Fourier-sorfejtésében szereplő amplitúdókat kell használni. Kitalálta, hogy ezeknek milyen algebrai szabályoknak kell eleget tenniök ahhoz, hogy a megfigyelésekkel egyező eredményt kapjon. Born és Jordan mutatták ki, hogy ezek a Heisenberg által az elektron helykoordinátájára és impulzusára használt matematikai szimbólumok mátrixok és nem kommutatív szorzási szabályoknak tesznek eleget. Heisenberg a dolgozatát 1925 júliusában közölte. Először Einstein sem hitt benne, Bohr is kételkedet, amíg Pauli mátrixmechanikával ki nem számolta a hidrogén-atom energia-sajátértékeit. Fél évvel később Ervin Schrödinger a de Broglie által 1924-ben bevezetett anyaghullám-fogalomból kiindulva jutott el egy differenciálegyenlethez, amelynek reguláris megoldásai adják az energia-sajátértékeket. Ő mutatta ki azt is, hogy a kétféle tárgyalásmód, a mátrixmechanika és a Schrödinger-féle hullámmechanika egymással egyenértékű. A közös néven kvantummechanikának nevezett elmélet az atomok és molekulák fizikai sajátságainak elméleti tárgyalásában a kezdettől fogva igen sikeres volt. A felfedezésétől eltelt háromnegyed század fizikája csak megerősítette azt az álláspontot, hogy a kvantummechanika mai tudásunk szerint az atomok és molekulák fizikai és kémiai sajátságainak legtökéletesebb elmélete.

Az elméletnek igen fontos eredménye, hogy az egymással fel nem cserélhető mennyiségek nem mérhetők egy időben tetszőleges pontossággal. A mérési hibáknak van a hatáskvantummal meghatározott korlátja. Ilyen mennyiségek, például az elektron helykoordinátája és a megfelelő impulzuskomponense, vagy az energia és az idő. Ezek a határozatlansági összefüggések, a mérés problematikája az atomfizikában, valamint az állapotfüggvény statisztikus értelmezése igen élénk vitákat váltottak ki, különösen a kezdeti időkben. Az 1927-ben rendezett Solvay-konferencián ezek az interpretációs és elvi kérdések voltak a viták középpontjában. Különösen Einstein volt az, aki a koppenhágai értelmezést nem tudta elfogadni. Késő éjszakáig tartottak a viták, a reggelinél újra kezdődtek. Einstein újabb és újabb gondolatkísérleteket talált ki az értelmezés cáfolatára, de Bohr és fiatal munkatársai mindig megválaszoltak rá. Einstein egész életében nem fogadta el a statisztikus értelmezést. Az értelmezéssel kapcsolatos tudományos értekezések hellyel-közzel azóta is előfordulnak, de a kvantummechanika eredményességét ezek nem érintik.

A fizikának csodálatos korszaka volt a huszadik század első harmada. Nagyszerű tudósok szép és igen hatásos alkotásai, a szokatlan új fogalmak, és a hozzájuk kapcsolódó, a régitől elütő gondolkodásmód képezték az elmélet letisztulását segítő vitákat. Werner Heisenberget az Eötvös Loránd Tudományegyetem 1964. március 5-én díszdoktorává avatta. Az avatási ünnepség keretében a részecskefizika aktuális kérdéseiről tartott nagy érdeklődést kiváltó előadást. Budapesti tartózkodása alatt alkalmunk volt vele személyesen is beszélgetni a kvantummechanika értelmezése körüli vitákról, magyar elméleti fizikusoknak a témakörhöz kapcsolódó munkáiról, és a modern fizika filozófiát is érintő kérdéseiről. Ezeket az emlékeinket felidézve, nagy tisztelettel emlékezünk reá, mint a huszadik század fizikáját alapjaiban meghatározó szellemi óriásra.