Fizikai Szemle 2003/9. 338.o.
BESZÁMOLÓ A 22. MIKOLA SÁNDOR FIZIKAVERSENY SOPRONI DÖNTŐJÉRŐL
A Mikola Sándor Országos Tehetségkutató Fizikaverseny tizedik osztályos döntőjét a hagyományoknak megfelelően a Vermes Miklós Országos Fizikus Tehetséggondozó Központ székhelyén, Sopronban bonyolították le 2003. május 10. és 13. között. A verseny meghirdetői: Vermes Miklós Országos Tehetséggondozó Központ, Eötvös Loránd Fizikai Társulat, Oktatási Minisztérium, Nyugat-Magyarországi Egyetem, a soproni Vas- és Villamosipari Szakképző Iskola és Gimnázium.
A verseny első, iskolai fordulóján, 2003. február 18-án több ezer 10. osztályos középiskolás indult a gimnáziumi és szakközépiskolai kategóriában. Az első fordulóban mindkét kategória versenyzői iskolai tanulmányaiknak megfelelő feladatlapot kaptak, és 3 óra alatt 6 feladatot kellett megoldaniuk. A szaktanárok elbírálása alapján 452 tanuló jutott a második fordulóba, amely a kijelölt megyei és fővárosi centrumokban 2003. március 25-én került megrendezésre.
A második fordulóban a résztvevőknek mindkét kategóriában 3 óra alatt 4 feladatot kellett megoldaniuk. A dolgozatokat a versenybizottság a Nyugat-Magyarországi Egyetem Fizikai Intézetének közreműködésével, szakmai irányításával Sopronban bírálta el. A második fordulóban elért eredményük alapján a 10. osztályosok közül 38 gimnazista és 12 szakközépiskolás jutott a döntőbe.
A döntőben, melyet a Vas- és Villamosipari Szakképző Iskola és Gimnáziumban rendeztek meg, a versenyzőknek az első napon 4 elméleti feladatot kellett megoldaniuk a rendelkezésre álló 180 perc alatt, majd a második napon egy kísérleti problémát kellett elemezniük 3 óra alatt.
Elméleti feladatok
Gimnázium 10. Osztály
|
1. feladat
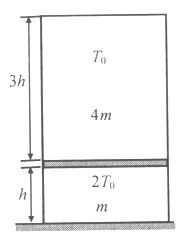
Függőleges, mindkét végén zárt hengerben lévő, súrlódásmentesen mozgó dugattyú a henger térfogatát az ábrán látható módon két részre osztja. Az alsó térrészben 2T0 hőmérsékletű, a felső térrészben T0 hőmérsékletű héliumgáz található. A felső térrészben lévő gáz tömege 4-szer nagyobb az alul elhelyezkedő gáz tömegénél. (h = 15 cm, T0 = 450 K.) Az ábrán látható helyzetből a hengert 180°-kal elfordítjuk, majd hagyjuk kiegyenlítődni a gázok hőmérsékletét. Ezt követően a két gáz hőmérsékletét úgy változtatjuk, hogy a továbbiakban azok nem különböznek egymástól.
a) Milyen közös hőmérsékletre kell felmelegíteni a rendszert, hogy a gázok térfogatai azonosak legyenek a kezdeti térfogataikkal?
b) Adjuk meg a gázok közös hőmérsékletét a dugattyúnak a henger aljától mért x távolsága függvényében!
c) A gázok melegítése során milyen maximális magasságig emelkedhet fel a dugattyú?
Kotek László, Pécs
|
 |
|
2. feladat
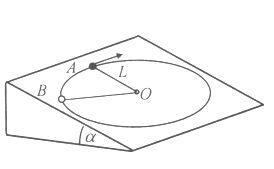
Egy kis átmérőjű korongot elhanyagolható tömegű, L = 0,2 m hosszúságú fonálhoz erősítünk, a fonál másik végét pedig egy 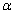 = 30° hajlásszögű lejtő felületéhez rögzítjük (O pont). A fonalat feszesen tartva a korongot az O középpontú, L sugarú kör legfelső pontjából, a lejtő síkjában vízszintes irányban meglökjük. A lejtő és korong között a csúszási súrlódási együttható = 30° hajlásszögű lejtő felületéhez rögzítjük (O pont). A fonalat feszesen tartva a korongot az O középpontú, L sugarú kör legfelső pontjából, a lejtő síkjában vízszintes irányban meglökjük. A lejtő és korong között a csúszási súrlódási együttható 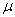 = 0,3, g = 10 m/s2. = 0,3, g = 10 m/s2.
Mekkora volt a kezdősebesség, ha a korong ß = 300°-os szögelfordulás után a B pontban tér le a körpályáról?
Szkladányi András, Baja
|
 |
|
3. feladat
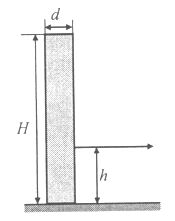
Egy indián szobrocska jó közelítéssel egy H = 6 cm magas, d = 1 cm átmérőjű tömör, homogén hengernek tekinthető. A szobrocskához az alaplaptól számított h = 2 cm magasságban cérnaszálat erősítünk, és a szobrocskát egy vízszintes asztallap közepére állítjuk. Egy vetélkedőn az asztal széléről, a vízszintes irányban feszített cérnaszállal magunkhoz kell húzni a szobrot, anélkül, hogy felborulna. Az asztal és a szobor között a súrlódási együttható 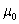 = = 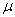 = 1/3. = 1/3.
Sikerülhet-e ez? Ha igen, hogyan, ha nem, miért nem?
Károlyházy Frigyes, Budapest
|
 |
4. feladat (választható az alábbi két feladat közül)
|
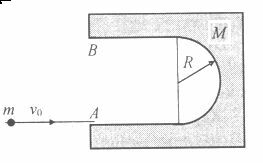
4.a Vízszintes, sima síkon U alakú, M tömegű építőkocka-kapu nyugszik, amelynek egyik szárához érintőleges pályán egy ugyancsak m = M tömegű, elhanyagolható sugarú korong érkezik v0 = 0,5 m/s sebességgel. Az U alakú kapu tömegközéppontja a félkörív körének középpontjában van. A kör sugara R = 10 cm, a kapu szárainak egyenes szakasza 2R hosszúságú. Minden súrlódás elhanyagolható.
a) Mekkora a két test sebessége akkor, amikor a korong a kapu B pontjába kerül?
b) Mennyi idő alatt teszi meg a korong az utat az A pontból a B pontba?
c) Hol lesz a kapu A pontja, amikor a korong a kapu B pontjába kerül?
Holics László, Budapest
|
 |
|
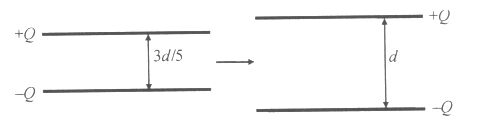
4.b Az U0 = 500 V feszültségre feltöltött, d lemeztávolságú síkkondenzátor belsejébe a lemezekkel párhuzamosan betolunk egy ugyanolyan méretű, 3d/5 lemeztávolságú, ugyanakkora töltésű síkkondenzátort.
a) Határozzuk meg a d lemeztávolságú kondenzátor feszültségét a betolás után! Vizsgáljuk mindkét esetet!
b) Hányszorosa az így kialakított rendszer energiája az eredeti, d lemeztávolságú kondenzátor energiájának?
Kotek László, Pécs
|
 |
Szakközépiskola 10. osztály
1. feladat (választható az alábbi két feladat közül)
|
1.a A mellékelt p-V állapotsíkon a hidrogéngáz három állapotváltozása látható. Az állapotsíkon az egyes folyamatokat ábrázoló szakaszok párhuzamosak. 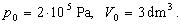
Milyen értékekkel kü1önböznek egymástól az egyes folyamatok megvalósításához szükséges hőmennyiségek?
Kopcsa József, Debrecen
|
 |
|
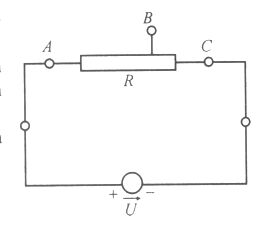
1.b A feszültségmérő eszköz Rm műszerellenállását egy elhanyagolható belső ellenállású feszültségforrás és egy R = 1200 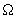 ellenállású tolóellenállás segítségével határoztuk meg. A B kivezetés a tolóellenállást 1/4 és 3/4 részre osztja. A műszer UAB = 12 V feszültséget jelzett, ha azt az A és a B, illetve UAC = 22 V feszültséget mutatott, ha azt az A és a C pontokhoz csatlakoztattuk. ellenállású tolóellenállás segítségével határoztuk meg. A B kivezetés a tolóellenállást 1/4 és 3/4 részre osztja. A műszer UAB = 12 V feszültséget jelzett, ha azt az A és a B, illetve UAC = 22 V feszültséget mutatott, ha azt az A és a C pontokhoz csatlakoztattuk.
a) Mekkora a műszerellenállás?
b) Milyen erősségű áram folyt át a feszültségforráson a két esetben?
Kopcsa József, Debrecen
|
 |
2. feladat
Egy vonat v0 = 24 km/h sebességgel halad át egy széles folyó javítás alatt álló hídján. Éppen amikor a vonat eleje a folyó hídjához ér, a kalauz állandó sebességgel elindul a vonat elejétől a vége felé. Végighaladva a vonaton a vonat vége éppen a túlsó partig jutott. Vegyük a vonatot egyterűnek, és az elejétől a végéig átjárhatónak!
a) Mekkora sebességgel mozgott a kalauz a vonathoz képest, ha a vonatnak 20%-kal kellett több idő a hídon való áthaladáshoz, mint a vonat elejének?
b) Hányszorosa a folyó szélessége a vonat hosszúságának?
c) Hányszor volt távolabb a kalauz a túlsó parthoz, mint a közelebbihez abban a pillanatban, amikor a vonat már félig legördült a hídról?
Kiss Miklós, Gyöngyös
|
3. feladat
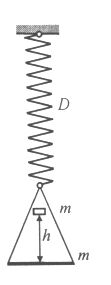
Egy D = 100 N/m direkciós erejű rugóra m = 1,8 kg tömegű serpenyőt függesztünk, amelyre bizonyos magasságból ráejtünk egy szintén m = 1,8 kg tömegű testet. A test és a serpenyő rugalmatlanul ütközik. A test és a serpenyő együttmozgása során megvalósult legnagyobb sebesség megegyezik a test ütközés előtti sebességével. g = 10 m/s2 , a közegellenállás elhanyagolható.
a) Mekkora közös sebességgel indul el a serpenyő és a test a rugalmatlan ütközés után, ha a test h magasságból esett?
b) Határozzuk meg h értékét!
Suhajda János, Kiskőrös
|
 |
4. feladat
Megegyezik a gimnazistáknak kiírt 3. feladattal
Kísérleti feladat
|
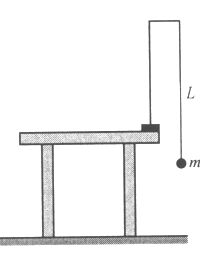
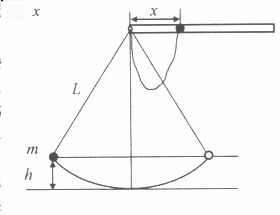
Húzóütközés energiaveszteségének vizsgálata fonálinga segítségével
Eszközök: állvány, matematikai inga, vonalzó, mérőszalag, milliméterpapír, függőón. A matematikai ingát úgy is lengésbe hozhatjuk, hogy az inga nehezékét a felfüggesztési ponton átmenő vízszintes egyenes egy adott pontjába visszük és ott kezdősebesség nélkül elengedjük. A kérdéses egyenesen vigyük a nehezéket a felfüggesztési ponttól x távolságra, és ott hirtelen engedjük el! Néhány lengés után az inga szabályosan lengeni fog. Jelölje h a lengés során (második bal oldali kilengés) a nehezék egyensúlyi helyzetéhez viszonyított maximális emelkedési magasságát! Továbbá jelölje 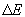 a vizsgált folyamat során bekövetkező mechanikai energiaveszteséget, E0 pedig a nehezék elengedésekor a nehezéknek a pálya legmélyebb pontjához viszonyított helyzeti energiáját! a vizsgált folyamat során bekövetkező mechanikai energiaveszteséget, E0 pedig a nehezék elengedésekor a nehezéknek a pálya legmélyebb pontjához viszonyított helyzeti energiáját!
|
 |
|
Feladatok
1. Mérjük meg, hogyan függ a h emelkedési magasság az x kitérítési távolságtól! Mérési eredményeinket foglaljuk táblázatba, és ábrázoljuk grafikusan!
2. Mérési eredményeink alapján képezzük a q = 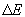 / E0 arányt, és ábrázoljuk a q arányt x függvényében! / E0 arányt, és ábrázoljuk a q arányt x függvényében!
3. Legyen *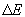 a fonál rugalmatlansága miatt bekövetkező energiaveszteség! Határozzuk meg elméletileg a q* = a fonál rugalmatlansága miatt bekövetkező energiaveszteség! Határozzuk meg elméletileg a q* =
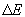 */ E0 hányadost, és ábrázoljuk x függvényében! Hasonlítsuk össze a g és q* értékeit és értelmezzük a különbséget! */ E0 hányadost, és ábrázoljuk x függvényében! Hasonlítsuk össze a g és q* értékeit és értelmezzük a különbséget!
Varga István, Békéscsaba
|
 |
Sopronban az ünnepélyes eredményhirdetésre május 13-án délelőtt került sor. A versenyzőket Nagy Márton, Vermes Miklós Országos Fizikus Tehetséggondozó Alapítvány ügyvezető igazgatója, a verseny főszervezője üdvözölte. Az eredményeket a versenybizottság (Holics László, Kotek László, Pápai Gyula, Suhajda János, Szkladányi András) nevében Kotek László (elnök) ismertette. Az első helyezetteknek járó Mikola-emlékérmet Nagy Márton adta át, a helyet adó iskola nevében Hegyi Ferenc igazgató köszönt el a tanulóktól.
A döntő színvonalát jelzi az élen végzett tanulók teljesítménye. A gimnáziumi kategóriában az első helyezett a maximális 60 pontból (40 pont elméleti feladat, 20 pont kísérleti feladat) 60 pontot ért el. Az első három helyen végzett tanuló teljesítménye százalékban: gimnáziumi kategóriában: 100%, 98,3%, 90%, szakközépiskolai kategóriában: 71,6%, 65%, 51,6%.
A döntőben szerepelt 37 gimnazista, illetve 12 szakközépiskolás átlagteljesítménye a kitűzött feladatokat illetően: 1. feladat (46,2%, ill. 60,8%), 2. feladat (63%, ill. 70,8%), 3. feladat (25,9%, ill. 30,8%), 4. feladat (33,2%, ill. 15%), kísérleti feladat (66,1%, ill. 49,2%).
A verseny végeredménye
Gimnáziumi kategória
1. KÓMÁR PÉTER, Fazekas Mihály Főv. Gyak. Ált. Isk. és Gimn., Budapest, felkészítő tanára: Dvorák Cecília
2. VARJAS DÁNIEL, Széchenyi István Gimnázium, Dunaújváros, Kispál István
3. NAGY RÓBERT, ELTE Apáczai Csere János Gyak. Gimnázium, Budapest, Pákó Gyula
4. PÁLINKÁS CSABA (Verseghy Ferenc Gimnázium, Szolnok, Pécsi István); 5. HORVÁTH ZOLTÁN (ELTE Apáczai Csere János Gyak. Gimnázium, Budapest, Pákó Gyula); 6. KISS PÉTER (ELTE Apáczai Csere János Gyak. Gimnázium, Budapest, Zsigri Ferenc); 7. SZÍJÁRTÓ ANDRÁS (Fazekas Mihály Főv. Gyak. Ált. Isk. és Gimn., Budapest, Takács Lajos); 8. BAZSÓ GÁBOR (Verseghy Ferenc Gimnázium, Szolnok, Szécsiné Festő Hegedűs Margit); 9. MARGETÁN ZSOMBOR (Pannonhalmi Bencés Gimn. és Koll., Pannonhalma, Rábai László); 9. MÉSZÁROS TAMÁS (Fazekas Mihály Főv. Gyak Ált. Isk. és Gimn., Budapest, Takács Lajos); 11. STRENNER BALÁZS (Teleki Blanka Gimnázium, Székesfehérvár, Szakály Edit); 11. SZÍJÁRTÓ LÁSZLÓ (Garay János Gimnázium, Szekszárd, Pesti Gyula); 13. MAYER PÉTER (Városmajori Gimnázium, Budapest, Ábrám László); 14. BUSTYA ÁRON (Szent László Ált. Művelődési Központ, Baja, Jaloveczki József); 14. FERENCZY MÁTÉ (Fazekas Mihály Főv. Gyak. Ált. Isk. és Gimnázium, Budapest, Dvorák Cecília); 16. FODOR BÁLINT (Batthyány Lajos Gimnázium és Szki., Nagykanizsa, Dénes Sándor); 17. KIRIAKOV SZILVIA (ELTE Apáczai Csere János Gyak. Gimnázium, Budapest, Zsigri Ferenc); 17. KIRILLY MIKLÓS (Berzsenyi Dániel Gimnázium, Budapest, Baranyai Klára); 19. GOSZTONYI BALÁZS (ELTE Radnóti Miklós Gyak. Gimnázium, Budapest; Markovits Tibor); 20. LÁSZKA ÁRON (ELTE Apáczai Csere János Gyak. Gimnázium, Budapest, Zsigri Ferenc); 20. TIBORI TAMÁS TIBOLD (DE Kossuth Lajos Gyakorló Gimnázium, Debrecen, Dudics Pál); 22. HANDBAUER PÉTER (Leőwey Klára Gimnázium, Pécs, Simon Péter); 23. ÁBRÁM DÁNIEL (Lévay József Ref. Gimnázium, Miskolc, Kerboltné Tóth Edit); 24. IVÁDY VIKTOR (Szilágyi Erzsébet Gimnázium és Koll., Eger, Burom Mária); 25. FRALLER BALÁZS (Zrínyi Miklós Gimnázium, Zalaegerszeg, Pálovics Róbert); 26. IVANICS PÉTER (Pannonhalmi Bencés Gimn. és Koll.. Pannonhalma, Rábai László); 27. VIG RÓBERT (Tóth Árpád Gimnázium, Debrecen, Kovács Miklós); 28. PÁL JENŐ (Piarista Gimnázium, Budapest, Futó Béla); 29. TURI ANDRÁSs (Teleki Blanka Gimnázium, Székesfehérvár, Szakály Edit); 30. LÁZÁR ENIKŐ MARINA (ELTE Apáczai Csere János Gyak. Gimnázium, Budapest, Pákó Gyula); 30. TÓTH LÁSZLÓ RICHÁRD (Berze-Nagy János Gimnázium és Szki., Gyöngyös, Kiss Miklós); 32. NÉMETH DÁNIEL (Veres Péter Gimnázium, Budapest, Varga Mária); 32. SERES GYULA (Fazekas Mihály Főv. Gyak. Ált. Isk. és Gimnázium, Budapest, Takács Lajos); 34. SZOLEK ANDRÁS (Berzsenyi Dániel Gimnázium, Budapest, Baranyai Klára); 34. SZOMOLÁNYI TAMÁS (Móricz Zsigmond Gimnázium, Szentendre, Rózsa Sándor); 36. HARASZTI RÓBERT (Deák Ferenc Gimnázium, Szeged, Horváth Vera); 37. ISZA PÉTER (Tóth Árpád Gimnázium, Debrecen, Kovács Miklós).
Szakközépiskolai kategória
l. PÉK ZOLTÁN, Puskás Tivadar Távközlési Technikum, Budapest, felkészítő tanára: Nagy Józsefné
2. FARKAS BALÁZS, Puskás Tivadar Távközlési Technikum, Budapest, Alapiné Ecseri Éva
3. OSÁN DÁNIEL, Pattantyús Áron Géza Ip. Szki., Győr, Sárándi Mária
4. HEGEDŰS PÉTER (Stromfeld Aurél Gép- és Építőip. Szki., Salgótarján, Kovács F. Gáborné); 4. INCZE ANTAL (Mechwart András Gépip. és Inf. Szki., Debrecen, Bánkné Zsebők Piroska); 6. NÉMETH ISTVÁN (Boronkay György Műsz. Szki. és Gimn., Vác, Arany Tóth László); 7. CSÉCSEI TIBOR (Cseháti Sándor Műsz. és Mg. Szki., Nagykanizsa, Marton László); 8. VANYÚR NORBERT Energetikai Szki. és Kollégium, Paks, Csajági Sándor); 9. KATZENBERGER PÉTER (Zipernowszky Károly Műszaki Szki., Pécs, Wagner Márta); 10. BOHNER ANDRÁS (Zipernowszky Károly Műszaki Szki., Pécs, Wagner Márta); 11. HERCZEG NÁNDOR (Pálfy János Műszer- és Vegyipari Szki., Szolnok, Mohácsi Ottó); 11. RÁCZ DÁVID (Gábor Dénes E.M.K., Debrecen, Gyebnárné Nagy Andrea).
A soproni döntőben a szervezők gondoskodtak a diákok kikapcsolódásáról is. Lehetővé tették a város múzeumainak, nevezetességeinek megtekintését. Igen nagy sikere volt és nagyon emlékezetes marad a résztvevők számára Károlyházy Frigyes professzor előadása.
A kerettanterv bevezetése továbbra sem teszi lehetővé az egységes feladatlapok készítését, hiszen az oktatás sorrendiségében nincs egységes szemlélet a magyar fizikaoktatásban. A versenybizottság nem akarta a tanulókat büntetni azzal, hogy 9. osztályban csupán mechanika feladatokat tűz ki, és 10. osztályban is még csupán választható feladat volt az elektromosságtan feladat. A következő évi versenykiírás már erőteljesen utal arra, hogy a Mikola Sándor Tehetségkutató Fizikaversenyen hamarosan az érvényben lévő tanterv, tankönyvek sorrendiségében kerülnek kitűzésre a feladatok. Így sokkal reálisabban tudunk egy-egy évfolyamon győztesek hirdetni. Reméljük ezzel a kollégák is egyetértenek, és tanulóik érdekében megteszik a szükséges változtatásokat.
Kotek László









