A4 feladat
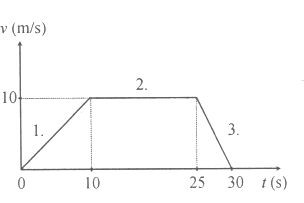
A grafikon a forgalomban haladó gépkocsi sebességét ábrázolja az idő függvényében.
a) Mekkora a gépkocsi gyorsulása az 1., a 2. és a 3. útszakaszon?
b) Mekkora utat tesz meg a gépkocsi az elindulástól a megállásig?
(Berkes József)
Fizikai Szemle honlap |
Tartalomjegyzék |
Fizikai Szemle 2003/10. 376.o.
A XIII. Öveges József Fizikaverseny megrendezésére Budapest után új helyszínen, Győrben, az Apor Vilmos Katolikus Iskolaközpontban került sor, 2003. május 16-18. között. Az országos döntőbe az iskolai, a területi (kerületi) és a megyei (fővárosi) fordulók után a 67 legjobb hazai diák jutott. A hagyományoknak és a lehetőségeknek megfelelően meghívást kaptak a határon túli országokban fizikát magyar nyelven tanuló diákok képviselői (Románia - 3 fő, Szerbia-Montenegró - 2 fő, Szlovákia 4 fő és Ukrajna - 2 fő) is.
A feladatkitűző bizottság munkáját a korábbi, jól bevált elképzelés alapján végezte. Az idei évben Berkes József, Ferencz János, Tóth Pál és Wöller László állította össze a döntő feladatait. A zsűri elnöke Molnár Miklós, a Szegedi Tudományegyetem docense volt.
Az új, a keleti országrésztől távolabb eső helyszín nem tette lehetővé a pénteki kezdést. A megérkezést követő helyfoglalás, illetve ebéd után a résztvevő diákok és kísérőik nagyobbik része az AUDI győri gyárának összeszerelő csarnokába látogatott. A többiek Péren a repülőteret nézték meg, és megkoszorúzták Öveges József iskolában elhelyezett emléktábláját. A vacsorát kulturális műsor követte.
A tényleges verseny szombaton kezdődött. Az országos döntő első részében az öt gondolkodtató (A) és a három összetettebb számítást igénylő (B) feladat megoldására került sor. Az előbbire 60 perc, az utóbbira pedig 120 perc jutott, közben 30 perces pihenővel, büfével. Mindegyik feladat megoldását a felügyelőtanártól kapott golyóstollal kétoldalas, indigós munkalapra kellett elkészíteni.
Az országos döntő második része az ebéd elfogyasztása után következett. A kísérleti (K), a kísérletelemző (E) és a fizikatörténeti (T) feladat megoldására egyaránt 40-40 perc állt a versenyzők rendelkezésére, közben 15 perces szünetekkel.
A délelőtti, illetve a délutáni feladatok megoldásának befejezése után a versenyzők magukkal vihették a feladatlapokat és a megoldásaik indigós másolatait. Egyúttal megtekintés céljából kifüggesztésre kerültek az egyes versenyfeladatoknak a feladatkitűzők által megadott megoldásai, illetve pontozási rendszere.
A hivatalos eredményhirdetés előtt lehetőséget adtunk a felkészítő, illetve a kísérőtanároknak az általuk vélt és indokolt reklamálásra, a kifogásolt megoldások értékelésének ismételt felülvizsgálatára. A reklamálást írásban, indoklással, az igényelt pontszám megjelölésével lehetett beadni. A 858 darab kijavított feladatra 13 felülvizsgálati kérelem érkezett, amelyből alapos elemzés után hármat tartott indokoltnak a versenybizottság.
A verseny befejezése után a diákok városnézésen vettek részt, Győr nevezetességeit tekintették meg vezetéssel. A résztvevő diákok a XIII. Öveges József Fizikaversenyen is térítésmentesen vehettek részt. A lebonyolítás költségeit pályázatokból, minisztériumi és egyéb támogatásokból biztosítottuk. Az Iskolaközpont vezetése és minden támogató, közreműködő segítségét köszönjük, melyre a továbbiakban is bizakodva számítunk.
Kitűzött feladatok
Gondolkodtató (A) feladatok
A1 feladat
Ősszel jól megfigyelhető, hogy a nagyobb városok felett gyakoribb és erőteljesebb a ködképződés, mint másutt. Mivel magyarázható ez a tapasztalat?
(Berkes József)
A2 feladat
Ma (2003. május 16-án) hajnalban ritkán megfigyelhető természeti jelenségnek lehettek szemtanúi a korán kelők. Teljes holdfogyatkozást lehetett megfigyelni.
a) Rajzold le az égitestek helyzetét!
b) Hogyan magyarázható ez a jelenség?
(Ferencz János)
A3 feladat
Az 1960-as római olimpián a 100 méteres síkfutás olimpiai bajnoka 10,2 másodperces idővel a német Armin Harry volt. Ugyanezt a számot 2000-ben, Sydneyben az amerikai Maurice Green nyerte meg 9,87 másodperces idővel. Egy képzeletbeli versenyen mekkora előnyt adhatna Green Harrynak, hogy pontosan egyszerre érjenek a célba? Tételezzük fel, hogy a távolságot mindegyik futó átlagsebességgel teljesíti!
(Ferencz János)
|
A4 feladat A grafikon a forgalomban haladó gépkocsi sebességét ábrázolja az idő függvényében. a) Mekkora a gépkocsi gyorsulása az 1., a 2. és a 3. útszakaszon? b) Mekkora utat tesz meg a gépkocsi az elindulástól a megállásig? (Berkes József) |

|
|
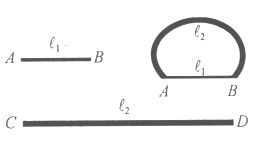
A5 feladat Két, azonos fémből készült kör keresztmetszetű huzal sugarainak aránya r1: r2 = 1:4, a hosszúságaik aránya pedig l1:l2 = 1:3. Kati a rövidebb huzal A és B végeit egy kisfeszültségű áramforrásra kötötte, és megmérte az áramerősséget. Ezután a két huzal végeit az ábra szerint egymáshoz erősítette. Ugyanazt az áramforrást az összeerősített A és B végekre kötve, megmérte a főágban az áramerősséget.
(Wöller László) |
 |
Számításos (B) feladatok
B1 feladat
A 200 cm3 űrtartalmú pohár félig van 50 °C hőmérsékletű vízzel. Mekkora tömegű -10 °C hőmérsékletű jeget és 10 °C hőmérsékletű vizet kell egyszerre beletenni ahhoz, hogy a pohár színültig megteljen és a víz hőmérséklete a termikus egyensúly létrejötte után 20 °C legyen? A pohár térfogatváltozásától és mindennemű veszteségtől eltekintünk.
A víz sűrűsége 1000 kg/m3, jég fajhője 2,1 kJ/kg°C olvadáshője 340 kJ/kg, a víz fajhője 4,2kJ/kg°C.
(Tóth Pál)
B2 feladat
Az 5 kg tömegű szánkóra 50 liter űrtartalmú, 50 N súlyú hordót helyeztek, melyet vízzel teletöltöttek. A szánkót állandó, 1,5 m/s nagyságú sebességgel húzták az elindulástól a 300 m távolságra lévő célig. Az indulást követően 50 s elteltével meglazult a hordó dugója, és a hordóból másodpercenként 1 dl víz távozott. A víz sűrűsége 1000 kg/m3.
(Wöller László)
|
"B3 " feladat Egy iskolai laboratóriumban a mellékelt kapcsolási rajz alapján összeállított berendezéssel méréseket végeztek a diákok. Mindkét áramforrás feszültsége 18 V, és mindegyik fogyasztó ellenállása 150 a) Melyik fogyasztók működnek, és mekkora erősségű áramot mutatnak az ampermérők, ha a
Mindegyik esetben készítsd el az átalakított kapcsolási rajzot! b) A kapcsolók melyik állásában lesz valamelyik R ellenállású fogyasztó teljesítménye a legnagyobb, illetve a legkisebb? Mekkorák ezek az értékek? (Berkes József) |
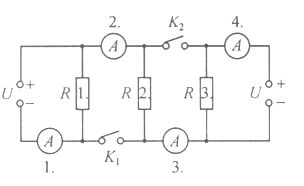
|
Kísérleti (K) feladat
A tálcán található eszközök segítségével határozd meg a borszeszégővel történő vízmelegítés hatásfokát! A mérés menetéről készíts részletes jegyzőkönyvet!
A tálcán található eszközök: 1 db borszeszégő, 1 db vasháromláb, 1 db azbesztbetétes drótháló, 1 db karos mérleg (mérőtest-sorozattal), 1 db 250 cm3-es főzőpohár, 1 db 500 cm3-es műanyagflakon, vízzel, 1 db hőmérő, 1 doboz gyufa.
A feladat megoldásához szükséges táblázati adatok:
a denaturált szesz égéshője: 30000 kJ/kg, a víz fajhője: 4,2 kJ/kg°C.
( Wöller László)
|
Kísérletelemző (E) feladat A 600 menetes tekercs belsejébe üvegcsövet, majd abba egy varrótűt helyeztünk úgy, hogy a varrótű bal oldali vége éppen a tekercs jobb oldali végénél legyen. Figyeld meg a következő jelenséget, és mindkét esetben adj magyarázatot a látottakra!
(Wöller László) | 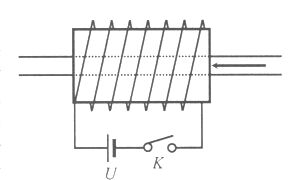
|
|
Fizikatörténeti (T) feladat A felkészüléshez megjelölt J.D. Bernal "A fizika fejlődése Einsteinig" című könyve segítségével megismerhetted a fizika fejlődéstörténetének legfontosabb állomásait, kiemelkedő kísérletezőit, feltalálóit, gondolkodóit, köztük a XVI-XVII. század nagy alakjának, Galileo Galilei, olasz természettudósnak életét és munkásságát. A fizikatörténeti rész kérdéseit, feladatait a fenti irodalom alapján állítottuk össze. A megoldásokat a keresztrejtvény játékszabályai szerint kell beírnod a négyzetekbe:
|  |
(Wöller László)
A díjazott versenyzők
I. díjas:
l. KŐRÖSI MÁRTON (116 pont, Békéscsaba, 9. sz. Általános Iskola, tanára: Kovácsné Bálint Judit)
II. díjasok:
2. NEMES ZSÓFIA (106, Szombathely, Bolyai J. Általános Iskola és Gimnázium, Pájer Szabolcs), 3. PÁLFI GYULA (106, Budapest, Apáczai Cs. J. Gimnázium, Zsigri Ferenc), EŐRY ZOLTÁN (105, Fertőd, Általános Iskola, Gáspár József). 5. TYUKODI BOTOND (103, Margitta, Általános Iskola, Rend Erzsébet), 6. NIGICSER BÁLINT (103, Érd, Bolyai J. Általános Iskola, Kántor Aranka), 7. VINCZE JÁNOS (102, Debrecen, Fazekas M. Gimnázium, Adorján László)
III. díjasok:
8. GARAMVÖLGYI TAMÁS (99, Beremend, Általános- és Zeneiskola, Prenek Józsefné), 9. BUTYKAI ÁDÁM (99, Miskolc, Földes F. Gimnázium, Zsúdel László), 10. KUNOVSZKI PÉTER (98, Mohács, Kisfaludy K. Gimnázium, Papp Csaba), 11. HORVÁTH CSONGOR MÁRK (97, Szombathely, Paragvári Utcai Általános Iskola, Ágoston Mária), 12. BALÁZS BÁLINT (96, Budapest, Árpád Gimnázium, Gärtner István), 13. NYIRI DÁVID (96, Debrecen, Református Kollégium Dóczy Gimnáziuma, Tófalusi Péter)
Ebben az évben negyedszer került átadásra a pénzjutalommal járó Öveges József-érem, melyet a verseny első helyezettje, KŐRÖSI MÁRTON (Békéscsaba) és felkészítő tanára, KOVÁCSNÉ BÁLINT JUDIT érdemelt ki. Az érmek névre szóló átadására, Keszthelyen, a XXVII. Általános Iskolai Fizikatanári Ankét és Eszközkiállítás megnyitó ünnepélyén került sor, melyre a versenyző és tanára vendégmeghívást kapott.
A zsűri a legjobb 13 versenyző teljesítményét (74,4% felett) díjazta. Minden díjazott versenyző Magyar Bálint miniszter által aláírt oklevelet kapott.
Minden versenyző a Chip Magazin egy-egy számát lemezmelléklettel, Győr városáról szép kivitelű, képekkel illusztrált könyvet, valamint várostérképet, méhecske kabalafigurát és egy erszényt kapott.
A III. díjas versenyzők könyveket, illetve a KöMaL egyéves előfizetését kapták.
A II. díjas versenyzők (A 2. helyezett könyvet, nagyméretű méhecske figurát, trikót, sálat és CD kazettát, tanára könyvet és a Természet Világa egyéves előfizetését kapta. A 3. helyezett könyvet, tollkészletet, CD kazettát, tanára bőrkötésű mappát kapott. A 4. helyezett az Iskolaközpont díját, egy szép könyvet, illetve kamerát, valamint az Élet és Tudomány egyéves előfizetését, az 5. helyezett órát, könyvet, Győrről kazettát, a 6. helyezett Casio kalkulátort, könyvet és az Élet és Tudomány féléves előfizetését, a 7. helyezett könyvet, névjegykártyát és az Élet és Tudomány féléves előfizetését kapta).
Az I. díjas versenyző egy szépkivitelű könyvet, Győr város díját, és az Öveges-érmet kapta 10000 Ft nettó összeg kíséretében az 1. díjas versenyző tanára az Öveges-éremben és a Mikola-díjnak megfelelő 30000 Ft bruttó összegben részesült, valamint a Természet Világa egyéves előfizetését kapta.
Berkes József
Pécs