PRÓBAÉRETTSÉGI: ELÉGTELEN

Az új, kétszintű érettségivel eddig csak véleményezésre kiküldött anyagok formájában találkoztam. Már ezek alapján sem vártam sok jót. Nem a két szinttel kapcsolatban vannak fenntartásaim (bár a középszint elnevezést nem nagyon értem, amikor nincs ennél alacsonyabb szint) - az évről-évre könnyebb érettségi és felvételi feladatsorok láttán az emelt szint némi reményre is adhatna okot. (Kérdés persze, hogy fogja-e valaki is az emelt szintet választani, ha ezt még a legrangosabb egyetemek se teszik kötelezővé a felvételihez.)

Nem szeretem a teszteket (feleletválasztós kérdéseket): gyakran előfordul, hogy több félig-meddig jó válasz van, vagy éppen egy se teljesen igaz, a tanulónak mégis ki kell választania pontosan egyet. Különösen a kritikusan, árnyaltan gondolkodó, tehetséges tanulók jutnak nehéz helyzetbe, miközben a felületes diák akár véletlenül is adhat jó választ. Korábban a biológia felvételi feladatsorokból mazsoláztak tanítványaim szép példákat. Álljon itt egy elrettentésül: "Két mennyiség közti viszonyt kell vizsgálni. A lehetséges válaszok: A - egyenes arányosság, B- fordított arányosság, C- nincs kapcsolat." A megoldókulcsból az is kiderült, hogy minden monoton növekedő függvény esetében (például négyzetes összefüggés) az A válasz a helyes. Ha két mennyiség között szinuszos kapcsolat van, gondolom C-t kell választani. Matematika tagozatos diákjaim persze hamar megtanulták, hogy a feladatok megoldásakor - elfelejtve a matematika- és fizikaórákon tanultakat - ilyen sajátos módon kell "gondolkodni".

A korábban kiküldött feladatsorokból egy feladat maradt meg élesen emlékezetemben. Az 1. ábrán látható sebesség-idő függvényt kellett elemezni, és megrajzolni a hozzá tartozó gyorsulás-idő függvényt. A grafikon egy pattogó (tökéletesen rugalmasan ütköző) labda mozgását ábrázolja. A javítási útmutató szerinti megoldás a 2. ábrán látható. Az útmutató külön kitért a kis köröcskék fontosságára (pontlevonás, ha nincsenek). A feladat kitűzői szerint ezekben a pillanatokban a testnek nem értelmezhető gyorsulása? Ha viszont a gyorsulás mindig negatív, akkor miért nem monoton csökken a sebesség? A feladat kitűzői láthatólag tanultak matematikát (szakadásnál nem deriválható a függvény), de nem értik a feladatban lévő fizikát: az ütközés nagyon rövid (de nem nulla!) ideig tart a mozgás többi részéhez képest, ezért a sebesség-idő grafikonon (majdnem!) függőleges szakaszok lesznek. Ezalatt a testnek, értelemszerűen, rövid ideig nagyon nagy pozitív gyorsulása van (3.ábra).

Ilyen előzmények után némi gyanakvással, de kíváncsian vártam, hogy megkapjam a május 26-án megírt próbaérettségi feladatait¹ és az általam tanított tizenegyedikesek munkáit. Egy tanuló kivételével mindenki emelt szintet írt, így először abba a feladatsorba lapoztam bele. Amikor pedig megláttam, hogy már az első két feladat megoldása hibás, ...

Nem akarok általánosságokat írni, ezért kénytelen vagyok végigelemezni a két feladatsor összes hibáját. Az emelt szint első két feladatával (feleletválasztós kérdések) mégis kivételt teszek. A javítási útmutatóban megadott válaszok (D és A) egyértelműen, nyilvánvalóan rosszak. Feltehetően felcserélték a két választ, mert a helyes megoldás A és D. Azonban egy érettségi feladatsornál egy ilyen hiba is megengedhetetlen, különösen akkor, ha az útmutató szerint: "A feleletválasztós kérdésekben csak az útmutatóban közölt helyes válaszra lehet megadni a pontot."

Nézzük tovább az emelt szintű feladatsort!

1. rész, 4. feladat: Az esőcseppek függőleges irányban esnek, 7 m/s sebességgel. Az esőcseppek nyomai a vízszintes pályán mozgó vonat ablakán a vízszintessel 30°-os szöget bezáró csíkok. Mekkora a vonat sebessége?

A megadott válaszok közül a B válasz körülbelül (egy tizedesre kerekítve) megegyezik a kiszámolt értékkel. De akkor nem így kellene fogalmazni a kérdést: "Körülbelül mekkora a vonat sebessége?" vagy: "Melyik értékhez áll legközelebb a vonat sebessége?" Lehet, hogy ez csak szőrszálhasogatás, de azt gondolom, hogy ez a feleletválasztós kérdések egyik típushibája. Szigorúan véve egyik válasz se jó.

7. feladat: A víz alatti hajóroncsra kalapácsával ráüt egy búvár. Ki hallja meg előbb: a víz alatt a delfin vagy az éppen a búvár feje fölött repülő sirály? A delfin és a búvár (sic!) azonos távolságra van a búvártól. A - A madár, B - A delfin, C- Egyszerre hallják meg. D - Egyik sem hallja (nem keletkezik hang).

Újra egy elírás, most nem a javítási útmutatóban, hanem a feladatlapon. Persze nem nagyon lehet másként érteni, mint ahogy a feladatkitűzők gondolták. De hogyan gondolták? A hang kibocsátásakor van a delfin és a sirály azonos távolságra? És merre úszik a delfin? Ha a delfin gyorsan távolodik, a sirály pedig közvetlen a víz felett száll (épp halászik), akkor lehet A vagy C is a helyes válasz.

(Persze, a tesztek megoldására jól felkészített diák kitalálja a feladatkitűző gondolatát, észreveszi, hogy mire találták ki ezt az életszerű kis feladatot, és helyesen válaszol.)

10. feladat: A borult, felhős éjszakák általában kevésbé hidegek, mint ugyanabban az időszakban derült, tiszta égbolt esetén. Miért?

Ez a feladat tetszik. A hősugárzást nagyon fontos tananyagnak tartom. Ismeretterjesztő előadásokon, olimpiai felkészítésen is szoktam tanítani. Tapasztalatom szerint legtöbb diák nem tanult róla.

12. feladat: Miért csökken a feltöltés után a telepről lekapcsolt síkkondenzátor feszültsége, ha a lemezek közé szigetelőanyagot juttatunk? ... D-Állandó marad a töltés, a kapacitás növekedett, így a feszültség csökken.

Az indoklás teljesen formális, a megoldáshoz nem a szigetelőanyagok elektromos viselkedésének ismeretére, hanem a függvénytáblázat képleteinek formális használatára van szükség. A kapacitás növekedése éppen a szigetelőanyag polarizációja miatt kialakuló térerősség- és feszültségcsökkenés következménye.

14. feladat: Két azonos hosszúságú és keresztmetszetű huzalt kötünk sorba. Az egyik rézből, a másik alumíniumból van. Az áramerősséget fokozatosan növeljük. Melyik huzal izzik fel előbb?

Milyen rézből? A (tiszta) alumínium fajlagos ellenállása nagyobb, mint a vörösrézé, de kisebb a sárgaréznél. Tegyük fel, hogy vörösréz. Akkor az alumíniumon több hő keletkezik, mint a rézen. Ebből még nem feltétlen következik az, hogy melegebb is lesz. Ez függ a környezettel való termikus kapcsolattól is. Tekintsünk el ettől is. A halvány, sötétvörös izzás körülbelül 600 °C-on kezdődik - de épphogy elkezdődik: az alumínium 660 °C-on olvad.

Szépen diszkutálható kérdés lenne, ha lehetne diszkutálni.

16. feladat: Hova kell nyúlnia a folyóban lazacra halászó medvének, ha sikeres akar lenni? A - Lejjebb és távolabb, mint ahol látja a halat. B- Lejjebb és közelebb, mint ahol látja a halat. C - Feljebb és távolabb, mint ahol látja a halat. D- Feljebb és közelebb, mint ahol látja a halat.

A hivatalos válasz: B. Ez a válasz rossz!

De a feladat is rossz. A feladat tisztességes megoldására a 240 perces teljes idő se biztos, hogy elegendő lenne. A víz alatti tárgyról nem keletkezik éles kép! Próbáljuk meg a hal képét úgy kiszámolni, hogy a halból két közeli fénysugarat indítunk azonos függőleges síkban (4. ábra).

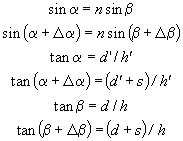
Felhasználva, hogy kicsi, ezért

és

az egyenletekből h'/h-t és d'/d-t kifejezve azt kapjuk, hogy mindkét érték bármely a értékre egynél kisebb, azaz a kép a rajzon is látható helyen keletkezik.

Eszerint a helyes válasz (hosszas, a diákoktól nem elvárható számítások után) A lenne.

De ez a válasz se jó! Ha nem két azonos függőleges síkban lévő, hanem két vízszintes (a rajzon a papír síkjára merőleges) irányban eltérő fénysugarat vizsgálunk, akkor más eredményt kapunk. Ekkor a hal képe a hal felett keletkezik - ilyen válaszlehetőség viszont az érettségiben nincs.

De ha lenne, akkor is nehéz lenne eldönteni, hogy a két ellentmondó megoldás közül melyiket válasszuk. (Ne feledjük, indokolni, diszkutálni nem lehet!) A térlátásban fontosabb szerepe van a két szemmel látásnak, mint az akkomodációnak, ezért a megoldás valószínűleg attól függ, hogy hogyan tartja a medve a fejét.

A feladatkitűző valószínűleg egy rossz rajzot látott valahol egy könyvben (egy tankönyvben?), és annak alapján adta fel a feladatot. Valószínűleg eszébe se jutott, hogy utánanézzen a problémának. Arra se gondolt, hogy az a diák, aki nem ugyanazt a könyvet vagy tankönyvet olvasta, mint a feladatkitűző, az hogyan jöhet rá a (szerinte) helyes megoldásra.

18., 19. és 20. feladat:

Atomfizika. A próbaérettségit 11.-esek írják. Azok, akik nem a kerettanterv szerint tanulnak, és a 12. évfolyamon is tanulnak fizikát (sok ilyen tanuló van), még biztosan semmit nem tanultak ebből, ezekre a kérdésekre legfeljebb tippelni tudnak. Miért kellettek ilyen feladatok a próbaérettségibe? A tanárok, a jövő évi érettségire készülő diákok tájékoztatására a próbaérettségitől függetlenül lehetne kiadni minta feladatsorokat - ezekben természetesen minden olyan tananyag szerepelhetne, ami az érettségi feladatsorban is előfordulhat.

Azzal, hogy az emelt szintű érettségin a feladatmegoldás mellett ilyen típusú feladat is helyet kapjon, alapjában egyetértek. (Bár szerintem ez tipikusan a szóbelire való feladat.) Egy komolyabb téma (például: megmaradási tételek a fizikában, gravitáló és tehetetlen tömeg) szöveges kifejtésével a tanuló a fizika mélyebb megértéséről adhatna tanúbizonyságot. Az itt szereplő három téma kidolgozásához viszont főleg adatokat, neveket, tényeket kell összegyűjteni (melyek jelentős része ráadásul megtalálható a függvénytáblázatban).

Ennél is elszomorítóbb a feladat pontozásához adott kicsinyes, bonyolult, épp a tényszerű adatokat és nem az összefüggéseket jutalmazó javítási útmutató. Nem hiszem, hogy egy esszé színvonalát a felsorolt (függvénytáblázatból kürt) adatok és fogalmak száma határozná meg. Azt se gondolom, hogy ettől lenne az értékelés objektív. A javítási utasítások elolvasásakor ugyanaz a rossz érzésem van, mint a feleletválasztós kérdések elemzése előtt idézett mondat olvasásakor ("...csak az útmutatóban közölt helyes válaszra lehet megadni... ").

III. rész, 1. feladat: Az 1000 kg tömegű, 100,8 km/h sebességű gépkocsi egyenletesen lassulva 84 m út megtétele után áll meg.

a) Hány másodperc alatt tette meg a gépkocsi a 84 m hosszúságú utat?

b) Mekkora utat tett meg a gépkocsi, amíg a sebessége a kezdeti érték felére csökkent?

c) Mekkora munkát végzett a fékezőerő a megállásig az autón?

Könnyű, hagyományos feladat. Mi ezzel a bajom? A 100,8 km/h-s kezdeti sebesség adat. Ez az adat szemléletromboló. Egy (véletlenül pontosan 1000 kg tömegű) autó sebességét nem életszerű tized km/h pontossággal mérni és megadni. Ez az érték visszafelé keletkezett: így lesz a m/s-ban mért sebesség (és a többi eredmény) egész szám. De ez vajon miért fontos a zsebszámológépek korában?

A feladat c) részének hivatalos megoldása viszont nemcsak szemléletromboló, hanem rossz is:

"A fékezőerő munkája megegyezik a mozgási energia megváltozásával. ( E= W alakban is megadható.)" Eddig jó, de ezután a hivatalos megoldás megfeledkezik arról, hogy az autó fékez, mozgási energiája csökken, és így természetesen W is negatív lesz.

"W= 1/2 mv², W= 392000 J" - ez a hivatalos, megkérdőjelezhetetlen válasz.

3. feladat: Sorba kötünk egy 110 V-os feszültségre méretezett, 50 W fogyasztású és egy 220 V, 200 W feliratú izzót a 220 V-os hálózati feszültségen. Hogyan fognak világítani a névleges teljesítményükhöz képest?

A hivatalos megoldás:

"A két ellenállás egyenlőségének indoklása: A fogyasztók ellenállása a teljesítménnyel kifejezve: R = U²/P. Az 50 W-os fogyasztó ellenállása: R₁ = 242 . A 200 W-os fogyasztó ellenállása: R₂ = 242 . (Az ellenállások egyenlőségének szöveges vagy paraméteres bizonyítása is elfogadható 6 ponttal, az értékek kiszámítása nélkül is.)

A fogyasztók feszültségének meghatározása: Mivel a két ellenállás egyenlő, mindkét izzón 110 V esik. (Számítással is elfogadható.)

Helyes válasz: A 110 V-os izzó a megadott teljesítménnyel működik (»rendesen világít«). A másik kisebb teljesítménnyel működik, halványabban világít."

A valóban helyes megoldás viszont így szól:

A két izzó üzemi (meleg) ellenállása megegyezik. Ha mindkettő üzemi hőmérsékletű lenne, akkor mindkettőre 110 V feszültség esne. De a 220 V-os izzó 110 V feszültség hatására jóval hidegebb, mint az üzemi feszültségen, ezért ellenállása is jóval kisebb lesz. Akkor viszont kisebb feszültség esik erre az izzóra, és nagyobb a 110 V-osra. Így a 220 V-os izzó még hidegebb, még kisebb ellenállású lesz, a 110 V-os pedig túlmelegszik, ellenállása tovább nő. A feszültségarány tovább romlik. Így a 110 V-os izzó biztosan kiég, és persze ezután egyik izzó sem fog világítani.

Hosszú évek óta foglalkozom a nemlineáris jelenségek tanításával (és ennek fontosságával). A példatárakban szereplő izzólámpás feladatokat, ahol az izzó ellenállását állandónak, hőmérséklettől függetlennek tekintik (pedig az közelítőleg sem állandó, egy nagyságrendet változik), elrettentő példaként szoktam idézni. Az izzó áram-feszültség karakterisztikájának kimérése (és ebből az izzószál hőmérsékletének meghatározása) nálam alapfeladat a 9. évfolyamon. Ez a tanulságos mérés olcsó és egyszerű. A legrosszabbul felszerelt iskolában is könnyen összeállítható több példányban: elvégezhetné minden tanuló. A kimért görbe segítségével a (jelentős belső ellenállású) zsebtelepre kapcsolt izzó munkapontja már egyszerű szerkesztéssel meghatározható.

Ez a feladat - a hivatalos megoldással - nagyon elszomorító. Tipikus példája a valóságtól elszakadt, fizikai szemléletet nélkülöző, öncélú feladatoknak, melyek elárasztják a példatárak és a tankönyvek jelentős részét. Ez az a feladat, amit az okos, gondolkodó tanuló old meg "rosszul". Az ilyen feladatok miatt éri sok (jogos) kritika a feladatmegoldás-centrikus fizikaoktatást. Pedig egy jó feladat (probléma) megoldása olyan szellemi kaland lehet, amely a fizika határain túlmutató élményt és tapasztalatot adhat.

4. feladat: Egy dugattyúval lezárt, hőszigetelt csőben 0,3 kg oxigéngáz van, melynek térfogata 0,1 m³. A bezárt gáz nyomása . A csőbe egy elektromos fűtőszál nyúlik be, melynek teljesítménye 400 W. Ezt a melegítőt 15 percen keresztül üzemeltetjük. Ez alatt az idő alatt a következő folyamat zajlik le: kezdetben a dugattyú állandó nyomása mellett a gáz 0,2 m³ térfogatra tágul, majd itt a dugattyú megszorul, és ekkor a gáz nyomása emelkedni kezd. Mekkora a nyomása a gáznak a folyamat végén? (A szükséges állandókat a függvénytáblázatból keresse ki!)

A feladat megoldásához persze semmilyen állandóra, sőt a feladatban megadott tömegre sincs szükség. Természetesen az ellen semmi kifogásom, hogy a feladatban olyan adat is szerepel, amire nincs szükség a megoldáshoz. Azt már kevésbé értem, hogy a javítási útmutató miért csak két hosszú, bonyolult, a végeredményben nem szereplő tömeget is felhasználó megoldás után harmadikként ismerteti a rövid, háromsoros, elegáns megoldást.

Nem egészen értem a "dugattyú állandó nyomása" kifejezést. Az ábrából úgy értelmezem, hogy a felütközésig (és nem megszorulásig!) a dugattyú szabadon mozoghat. Szabadon mozgó dugattyú esetén a gáz nyomása a külső légnyomással azonos. A megadott, szokatlan nagyságú () külső légnyomáshoz legalább valamilyen indoklás kívánkozik.

Középszint, I. rész (feleletválasztós kérdések), 7. feladat: Az alábbi kérdések közül melyik reverzibilis (megfordítható)? A - Az inga csillapodó rezgése B - A leeső üvegpohár összetörik C - A leeső gumilabda mozgása D Egyik sem.

Én - ebben az összefüggésben - biztosan C-t válaszolnék. A és B hangsúlyozottan irreverzibilis. A leeső gumilabda mozgása... Meddig? Visszapattanásról nincs szó. A szabadesés - kis sebességeknél, ha elhanyagoljuk a légellenállást - reverzibilis. De ha tovább gondolom a mozgást: az első felugrásig, ami majdnem olyan magas, mint a kezdő helyzet (középszinten csak teljesen rugalmatlan és tökéletesen rugalmas ütközést tanul egy diák), akkor is a reverzibilitás jut az eszembe. Persze, sok ütközés után a pattogó gumilabda is meg fog állni. A reverzibilitás időskála kérdése.

Mérlegelni itt sem lehet. A hivatalos válasz: D. Vitatkozni se lehet vele (a labda idővel tényleg megáll). Legfeljebb megkérni a feladatkitűzőt, hogy mondjon egy valóságos, reverzibilis folyamatot.

9. feladat: Az autórádió csak akkor használható, ha az antenna a karosszérián kívül van. A mobiltelefont enélkül is használhatjuk az autóban. Mi ennek az oka?

A - ... B - A rádióadók által használt elektromágneses hullámokat az autó fémkarosszériája leárnyékolja, míg a mobiltelefon-hálózatok által használt sokkal nagyobb frekvenciájú sugárzást nem. C - ...

De miért nem? Ez csak formális ok. Miért a frekvencia szerepel az indoklásban, és nem a hullámhossz? (Persze a kettő összefügg.) Az árnyékolás bonyolult és nehéz probléma. Nehéz jól indokolt választ adni, de lehet vele kísérletezni: például három réteg alumíniumfóliába csomagolva már nem szólal meg a mobiltelefon. Ugyanakkor fémdobozba zárt mobiltelefon esetében az árnyékolás függ az árnyékoló doboz méretétől is.

A városi forgalomban tapasztalataim szerint minden második, harmadik vezető kihangosítás vagy fülhallgató nélkül használja a mobiltelefont - pedig ez veszélyes és tilos. A feladat második mondata úgy is értelmezhető, hogy szabad. Egy fizikafeladatban még ilyesmire is kell figyelni.

13-14. feladat: modern fizika. Lásd emelt szint, I. rész, 18-20. feladat.

16. feladat: Az -sugárzás pozitív töltése miatt erősen ionizál, viszont már néhány centiméteres levegőrétegben is elnyelődik. A -sugárzás semleges, viszont jóval nagyobb az áthatolóképessége. Ennek alapján melyik veszélyesebb biológiai szempontból egy körülbelül 1 m-re lévő sugárforrás esetén? Az állítások azonos intenzitású és energiájú sugárzásokra vonatkoznak.

"Ennek alapján...": Az -sugárzás pozitív töltése miatt ionizál. Ha a -sugárzás semleges, akkor nem is ionizál? Akkor veszélyes-e egyáltalán? Persze, aki észreveszi, hogy az néhány cm-en belül elnyelődik, tehát 1 m-re már el se ér - rájön, hogy csak a másik lehet a jó megoldás. Akkor is, ha nem tud semmit a radioaktív sugárzásokról.

II. rész, 1. feladat: Egy modellvasút 30 dkg tömegű mozdonya 2 m sugarú körpályán egyenletesen halad. Egy teljes kört 3,7 s alatt tesz meg.

a) Mekkora a mozdony sebessége és lendülete?

b) Mekkora oldalirányú erővel nyomja a sín a mozdony kerekét?

c) Legfeljebb milyen magas lejtőre tud felgurulni a mozdony a feladatban szereplő kezdeti lendülettel, ha motorját a lejtő alján kikapcsolják? (g = 10 m/s² közelítő érték használható.)

Miért számoljunk egy olyan feladatban, ahol úgysem egész számok szerepelnek g = 10 m/s² értékkel? Ez 2% hiba, teljesen feleslegesen - a számológépbe nem sokkal több idő beütni a 9,81-et, mint a 10-et.

Kicsit gyors is ez a játékmozdony, több mint 12 km/h a sebessége, akkora, mint egy futó embernek. Ha nincs eléggé lent a súlypontja, fel is borulhat. Lehet, hogy az eredeti feladatban ez is kérdés volt, mert (g = 10 m/s² esetében) pontosan 60°-os szöget zár be a sín által kifejtett vízszintes és függőleges erő.

A lejtő magasságára (g = 10 m/s²-tel számolva) 0,58 m jön ki. Ezt a hivatalos megoldás 0,6 m-re - egy tizedesre, felfelé kerekíti. Pedig az adatok (3,7 s, 10 m/s²) két tizedes pontosságúak. A felfelé kerekítés ellen szól az is, hogy a mozdonyra súrlódás is hat. (Ez abból derül ki, hogy a lejtő elérése előtt, az egyenletes haladáshoz, be volt kapcsolva a motorja.)

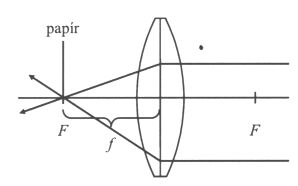
2. feladat: Egy vékony gyűjtőlencsével erős napfényben meg tudunk gyújtani egy papírdarabot, ha 20 cm távolságra tartjuk a lencsétől.

a) Készítsen a fénysugarak menetéről olyan rajzot, amely a papírdarabot és a fókusztávolságot is a megfelelő helyen mutatja! (A papírdarabot elég egy vonallal jelölni.) Adjon rövid magyarázatot arra, hogy miért azon a helyen gyullad meg a papír!

b) Hány dioptriás a lencse?

c) Milyen közel kell tenni a papírlapot a lencséhez, ha a lencsét nagyítónak használva, a papírlapot négyszeres nagyításban szeretnénk látni? Készítsen rajzot a képalkotásról, és számítsa ki a papírlap helyét!

A hivatalos megoldás rajza az a) feladathoz: A rajzon a fénysugarak a lencse közepén törnek meg. A Nap fénye a rajz és a szöveg szerint is egy ponton megy át, pedig a valóságban egy kicsiny (kb. 2 mm átmérőjű) folt lesz a Nap képe.

A sokkal-sokkal nagyobb baj viszont a c) kérdéssel van. Egy 20 cm-es fókusztávolságú lencsét nem lehet úgy tartani, hogy a papírlapot négyszeres nagyításban lehessen látni! Az, hogy a papírt a nagyítóval négyszeres nagyításban látjuk, azt jelenti, hogy a nagyítón át nézve a papírról négyszer akkora kép keletkezik a retinánkon, mint a nagyító nélkül. Tehát a szögnagyítást kell vizsgálni. Egy egyszerű nagyító szögnagyítása viszont (mint ahogy a függvénytáblázatból is kiderül) legfeljebb 1 + d/ f lehet, ahol d 25-30 cm a tisztánlátás távolsága. f = 20 cm esetén tehát legfeljebb 3-szoros lehet a szögnagyítás. A helyes válasz tehát az, hogy a lapot nem lehet a feladat feltételeinek megfelelően tartani.

A feladat kitűzője összekeveri a nagyítást a szögnagyítással. A hivatalos megoldás - teljesen hibásan - azt számolja ki, hogy hová kell rakni a papírlapot ahhoz, hogy egy négyszeres nagyítású virtuális kép keletkezzen. Ekkor viszont a kép 60 cm távolságra keletkezik a lencse mögött. Ilyen messziről viszont - hiába négyszer nagyobb a virtuális kép - csak körülbelül kétszer nagyobbnak látjuk a papírlapot, mint nagyító nélkül (a tisztánlátás távolságából). A feladatkitűző logikája szerint akár százszoros nagyítással is lehetne nézni a papírlapot: a tárgyat t = 19,8 cm távolságra kéne rakni a lencsétől, a kép pedig -k = 19,8 méter távolságra keletkezne! (Persze, ahogy közelítjük a tárgyat a fókuszhoz, már sokkal hamarabb "szétfolyik" a kép a lencse tökéletlenségei miatt.)

Mindezt ki lehet próbálni, csak kézbe kell venni egy 20 cm fókusztávolságú lencsét.

3/B feladat: Anna, Béla és Cili hideg narancslevet szeretne inni, ezért a pincértől jéggel kérik. Anna és Béla 8-10 °C hőmérsékleten szeretné fogyasztani, Cili pedig jégkása formájában. Amikor a pincér a három egyforma italt felszolgálja, Anna egy részét megissza a narancslének. De mivel az még körülbelül szobahőmérsékletű, elhatározza, hogy inkább vár még, a többiek is azt teszik. (A narancslé fagyáspontja közel van a 0 °C-hoz, és a jég mennyisége elég ahhoz, hogy jégkása képződhessen.)

a) Ezután ki kezdhet legkorábban inni, ha a kívánt hőmérsékleten akarja italát fogyasztani? Milyen időbeli sorrend alakul ki e tekintetben?

b) Ki tudja legtovább halogatni az ivást? Itt is állítson fel sorrendet a három személy között!

c) Állapítson meg sorrendet arra nézve, hogy kinek áll rendelkezésére a leghosszabb időtartam itala kívánt hőmérsékleten való elfogyasztásához!

A válaszokat indoklással adja meg!

Nem tudom, mit ért a feladatkitűző jégkásán. A feladat szövegében leírt esetben a narancslé lehűl 0 °C-ra, és ebben a folyadékban jégkockák úsznak. Ez nem jégkása.

A hosszú szöveges megoldást nem írom le, csak két részletre térek ki:

A b) részben a hivatalos megoldás szerint Anna itala hamarabb melegszik fel, mint Béláé, de ezt az útmutató nem indokolja. Nem is biztos, hogy ez így van! Anna leitta a meleg, szobahőmérsékletű narancslé egy részét, de ezzel nem változott meg italának energiadeficitje a szobahőmérséklethez képest. Feltéve - nem biztos, hogy jogos ez a feltevés -, hogy a poharak ugyanannyi hőt kapnak időegységenként a környezettől, az italok energiadeficite később is egyforma lesz. Ebből viszont az következik, hogy amikor Béla itala újra 8-10 °C lesz, akkor Anna kisebb tömegű itala még hidegebb lesz - tehát a hivatalos megoldással szemben Béla itala melegszik fel hamarabb.

Persze ebben a feladatban rengeteg a feltevés, a tisztázatlan körülmény. Majdnem minden állítás ellenkezőjét is meg lehet indokolni. A c) rész megoldásában a hivatalos megoldás is óvatosabban fogalmaz: "A jégkásaállapot a jég teljes elolvadásáig tart, így feltételezhetően ez a leghosszabb ideig tartó folyamat, míg a hőmérséklet-tartományokon való átmenet (hűléskor és melegedéskor) feltételezhetően rövidebb ideig tart." Persze, ha kevesebb a jég, és a pohár jobb hőszigetelő, akkor éppen a hivatalos megoldás fordítottja jön ki. De a javítási útmutató itt is csak az indoklások, megfogalmazások módjában engedékeny. Az fel sem merül, hogy - megfelelő indoklással más eredmény is teljes pontszámmal elfogadható lenne.

<>

A végére értem. A hibajegyzék is majdnem olyan hosszú, mint a feladatlapok. Szerencsére ez az idei feladatsor csak próba. A tanulókat nem érte helyrehozhatatlan kár. De mi lesz jövőre? Mi lesz, ha a tanulók egy megoldhatatlan feladattal idejük jelentős részét elpocsékolják? Mi lesz, ha az emelt szintű érettségin az ismeretlen javítók a hivatalos javítókulcs szerint fognak pontozni, és az okos, gondolkodó, valóban helyes választ adó diákok fognak rosszabb eredményt elérni?

A próbaérettségi értékelése: elégtelen. Ki a felelős érte? Mi a biztosíték arra, hogy jövőre ez a peches évfolyam, amely tanulmányai közepén már kénytelen volt átélni egy tantervváltoztatást, tisztességes feladatsort fog kapni?

1 A feladatok és a javítási útmutatók megtalálhatóak a http://www.om.hu/okev internetcímen.