ÖVEGES JÓZSEF FIZIKAVERSENY - Győr, 2004

A XIV. Öveges József Fizikaverseny megrendezésére Győrben, a Kazinczy Ferenc Gimnáziumban került sor, 2004. május 21-23. között. Az országos döntőbe 67 hazai diák jutott, de a hagyományoknak megfelelően meghívást kaptak a határon túli országokban fizikát magyar nyelven tanuló diákok képviselői (Romániából 4 fő, Szlovákiából 4 fő és Ukrajnából 2 fő) is.

A döntő feladatainak kitűzői ebben az évben: Berkes József, Farkas László, Ferencz János és Wöller László. A zsűri elnöki tisztére Hadházy Tibor, a Nyíregyházi Főiskola tanszékvezető főiskolai tanára kapott felkérést.

A tanulók pénteken érkeztek a verseny színhelyére. A regisztráció, a szállás elfoglalása és az ebéd után a megnyitó következett a városháza dísztermében, melyen részt vett Horn Gábor államtitkár is. A megnyitó után a versenyzők és kísérőik megtekintették a Czuczor Gergely Bencés Gimnáziumban a Jedlik-kiállítást, és koszorút helyeztek el Jedlik Ányos szobránál.

A vacsorát követően Zsoldos Tamásné Öveges József élete és munkássága címen tartott előadást, melynek anyagát tartalmazó füzetet minden versenyző megkapta. Ezután Pintér Ambrus atya, a pannonhalmi Bencés Gimnázium fizikatanára egy számítógéphez kapcsolható, mozgó mechanikai alkatrészek nélküli gyorsulásmérőt mutatott be.

A szombaton kezdődő országos döntő első részében a hat gondolkodtató ("A") és a három összetettebb, bonyolultabb számítást igénylő ("B") feladat megoldására került sor. Az előbbire 60 perc, az utóbbira 120 perc jutott. A döntő második része ebéd után következett. A kísérleti ("K"), a kísérletelemző ("E") és a fizikatörténeti ("T") feladat megoldására egyaránt 40-40 perc állt a versenyzők rendelkezésére. Mindegyik feladat megoldását a felügyelőtanártól kapott golyóstollal kétoldalas, indigós munkalapra kellett elkészíteni.

A délelőtti, illetve a délutáni feladatok megoldásának befejezése után a versenyzők magukkal vihették a feladatlapokat és megoldásaik indigós másolatait. Megtekintés céljából kifüggesztésre kerültek az egyes versenyfeladatoknak a feladatkitűzők által megadott megoldásai, illetve pontozási rendszere.

Az effektív verseny befejezése után Zombori Ottó A harmadik évezred csillagképei a Kárpát-medence felett címmel tartott eladást. A vacsora után a verseny résztvevőinek a Kaláka Együttes adott nagysikerű koncertet.

A hivatalos eredményhirdetés előtt lehetőséget adtunk a diákoknak, illetve kísérőtanáraiknak az általuk vélt és indokolt reklamálásra, a kifogásolt megoldások értékelésének ismételt felülvizsgálatára. A reklamálást írásban, indoklással, az igényelt pontszám megjelölésével lehetett beadni. A 924 darab kijavított feladatra 3 felülvizsgálati kérelem érkezett, amelyet a versenybizottság alapos elemzés után nem tartott indokoltnak.

A díjkiosztó ünnepélyen jelen volt az ELFT elnöke, Németh Judit is. Az Öveges József Érmet, a verseny első helyezettje, SZIRMAI PÉTER (92,2%) és felkészítő tanára, Monus Tibor érdemelte ki. A versenybizottság a legjobb 16 versenyző teljesítményét (78,2% felett) díjazta. Minden díjazott versenyző Magyar Bálint oktatási miniszter által aláírt oklevelet kapott.

A részt vevő diákok a XIV. Öveges József Fizikaversenyen is térítésmentesen vehettek részt. A lebonyolítás költségeit pályázatokból, minisztériumi és egyéb támogatásokból biztosítottuk.

Az első három feladatban megfogalmazott négy kijelentés közül egy nem igaz. Karikázd be a feladatlapon, illetve írd az indigós munkalapra a hamis állítás betűjelét! Indokold meg, hogy a kiválasztott állítás miért nem igaz!

1. Az asztalra helyezett test súlya az asztalra hat.
2. A test sebességváltozása csak a testre ható erő nagyságától függ.
3. A két test között fellépő súrlódási erő nagysága független az egymással érintkező felületek nagyságától.
4. Ha a test egyenes vonal mentén állandó sebességgel mozog, akkor a testre ható erők eredője zérus.

1. Ha a daru felemel egy testet, akkor a gravitációs mező energiája nő.
2. Ha a daru függőlegesen és állandó sebességgel emeli a testet, akkor az egyenlő útszakaszokon végzett munkája és teljesítménye is állandó.
3. Ha a daru ugyanakkora állandó sebességgel a 2 m tömegű testet kétszer magasabbra emeli fel, mint az m tömegű testet, akkor a végzett munkája és teljesítménye is kétszeresére nő.
4. Ha a daru függőlegesen és egyenletesen gyorsulva emeli a testet, akkor az egyenlő útszakaszokon végzett munkája állandó, a teljesítménye viszont nő.

1. Ha a víz hőmérséklete csökken, akkor a sűrűsége nő.
2. Ha az alumíniumból készült csavaralátét hőmérséklete csökken, akkor a lyuk átmérője is csökken.
3. A lefedett levesestál fedőjére lecsapódó vízgőz melegíti környezetét.
4. A tanteremben lévő tanulói szék fa ülőkéjét kezünkkel érintve magasabb hőmérsékletűnek érezzük, mint a vasból készült lábát.

A piros és a kék golyóról a következőket tudjuk:

• Az egyik puha, a másik kemény fémből készült.
• Ha a golyókat olyan, vízzel félig töltött mérőhengerekbe tesszük, ahol az alaplapok átmérőinek aránya 2, akkor a vízszintemelkedések aránya 1/4.
• A vízszintes talajon, ha egyenlő nagyságú, ellentétes irányú sebességgel ütköznek, akkor a közös sebességük nagysága az eredeti sebességük nagyságának fele lesz.

Hogyan aránylik a piros és a kék golyó sűrűsége a két golyó átlagsűrűségéhez?

Csilla a műanyag flakont 9/10-ed részéig forrásban lévő vízzel töltötte meg, majd dugóval lezárta. Rövid idő elteltével a flakonban lévő vizet összerázta, és a dugó a flakonból kirepült.

Vajon miért? Add meg a helyes magyarázatot a tapasztalt jelenségre!

A két ugyanolyan ellenállású fogyasztót először sorosan, majd párhuzamosan kapcsolták egy-egy áramkörbe. A mért áramerősség mindkét esetben megegyezett.

1. Mekkora az áramforrások feszültségének aránya?
2. Mekkora az áramforrások teljesítményének aránya?

Három gépjármű (A, B és C) halad egyenletesen az úttesten. Az A jelű mögött halad a B, és velük szemben a C. Az A tömege 1,5-szerese a B tömegének, míg a C tömege 75%-a az A tömegének. A C sebessége 20 m/s. Az A sebessége 10 m/s a B jelű gépjárműhöz viszonyítva. Az A gépjármű lendülete kétszerese a C lendületének. Egy adott pillanatban az A 1 km távolságra volt a C jelűtől és B jelűtől is.

1. Mennyi idő múlva találkozik a Cjelű az A jelűvel és a B jelűvel?
2. Mekkora a három jármű mozgási energiájának aránya? (A, B, C sorrendben)

Egy 15 cm x 20 cm alapélű, 30 cm oldalélű egyenes hasáb alakú edényt 2/5 részéig öntöttek vízzel. A vízbe merülőforralót tettek a másnapra tervezett melegítéshez. Reggelre azonban a hideg éjszakán a víz -3 °C-os jéggé fagyott. A merülőforralót ilyen körülmények között kapcsolták a 230 V feszültségű hálózati áramforrásra.

Hány percig kellett a merülőforralót üzemeltetni, hogy 40 °C hőmérsékletű vízhez jussanak?

A króm-nikkel fűtőszál hossza 1,4 m, a keresztmetszete 0,03 mm². Az 1 m hosszú és 1 mmz keresztmetszetű króm-nikkel huzal ellenállása 1,2 . A melegítés hatásfoka 75%. A jég fajhője 2,1 kJ/kg°C, az olvadáshője 336 kJ/kg, víz sűrűsége 1000 kg/m³, a fajhője 4,2 kJ/kg°C.

A kapcsolási rajzon látható transzformátor primer tekercsére kapcsolt feszültség 230 V, a primer tekercs menetszáma 10000, a szekunderé 2000. Az R₁ jelű ellenállások értéke 100 .

1. Ha a 30 cm hosszú változtatható ellenállás harmadát iktatták az áramkörbe, akkor mindhárom ellenállás kivezetésein azonos feszültséget mértek. Mekkora erősségű áramot mutattak ekkor az ampermérők?
2. Hányszorosára változik meg a primer körben az áramerősség, ha a változtatható ellenállást teljes hosszában az áramkörbe iktatják?
3. Írd fel és ábrázold a primer körben mérhető áramerősséget a változtatható ellenállás áramkörbe iktatott hosszának függvényében?

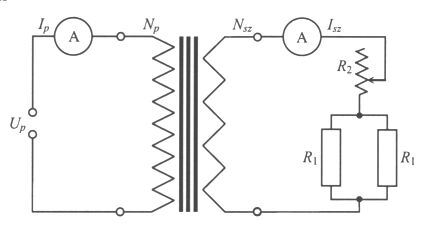
A feladat megoldásánál mindennemű veszteségtől eltekintünk.

A kísérletező tanár két vasmagos tekerccsel, melyek sorosan vannak kapcsolva egy zsebtelepre, próbál felemelni egy vashasábot úgy, hogy a tekercsek vasmagjait a vashasáb végeihez közelíti. Ez először sikerül is neki, de amikor az egyik tekercs kivezetéseire kapcsolt vezetékeket felcserélve, vagy az egyik tekercset 180°-kal elforgatva szeretné megemelni a hasábot, kudarcot vall.

Elemezd a látottakat, és add a magyarázatát!

A rendelkezésedre álló eszközök segítségével végezz méréseket és határozd meg, hogy mekkora az 1 m hosszú 1 mm² keresztmetszetű ceruzabél (grafitszál) ellenállása! Rajzold le a mérés kapcsolási rajzát, és a mérés menetéről készíts részletes jegyzőkönyvet! A ceruzabél átmérője: 2 mm.

Eszközök: preparált ceruzabél, zsebtelep, V-A mérő, vezetékek, krokodilcsipeszek, vonalzó.

A következő fizikatörténeti feladat az angol Isaac Newton életével és munkásságával kapcsolatos. Mindegyik kérdésnél a három válasz közül csupán egy a helyes. Az általad helyesnek vélt válasz betűjelét írd az előtte lévő üres keretbe! Minden helyes válasz egy pontot ér.

I. díjas: 1. SZIRMAI PÉTER (118 pont, Kisvárda, Vári Emil Általános Iskola, tanára: Monus Tibor)

II. díjasok: 2. LŐRINCZ ZSUZSANNA (113, Fertőd, Általános Iskola, Gáspár József és Pápai Gyuláné), 3. CSATÓ BERTALAN (112, Győr, Révai Miklós Gimnázium, Németh Lajos)

III. díjasok: 4. TIBORCZ LÍVIA (107, Tata, Vaszary János Általános Iskola, Maráz Lászlóné), NAGY ZSOLT (107, Pécs, PTE Gyakorló Gimnázium és Általános Iskola, Sebestyén Zoltánné), FERENCZ ENDRE (107, Szatmárnémeti (RO) Főgimnázium, Mártin Csilla), 7. HULLÁR DÁVID (106, Tiszabercel, Bessenyei György Általános Iskola, Lipcseiné Nemcsik Edit), 8. SZOLNOKI LÉNÁRD (104, Debrecen, Református Kollégium Dóczy Gimnáziuma, Tófalusi Péter), PÁSZTOR ÁRPÁD (104, Debrecen, DE Gyakorló Gimnáziuma, Kirsch Éva), HEGYI ÁDÁM (104, Eger, Dobó István Gimnázium, Hóbor Sándor), DEMETER DÁNIEL (104, Pécs, Testvérvárosok Terei Általános Iskola, Sebestyén Zoltán), ÁBRAHÁM GERGŐ (104, Lenti, Vörösmarty Mihály Általános Iskola, Baloghné Bedő Judit), 13. HORVÁTH BALÁZS (102, Budapest, Gábor Áron Általános Iskola, Kertész Ilona), 14. KÁLVIN BALÁZS (101, Dorog, Eötvös József Általános Iskola, Guhn Ferencné), CSALLÓKÖZI DÁVID (101, Kazincbarcika, Pollack Mihály úti Általános Iskola, Polyák István), 16. PARASZTI ISTVÁN (100, Nagymegyer (SK) Bartók Béla Magyar Tannyelvű Alapiskola, Nagy Teréz)

Berkes József, PTE