
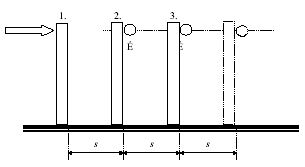
1. ábra Dőlő dominósor
Fizikai Szemle honlap |
Tartalomjegyzék |
Vannay László, Fülöp Ferenc, Máthé József, Nagy Tamás, Vankó
Péter
BME TTK, Fizikai Intézet, Kísérleti Fizika Tanszék
A Fizika Országos Középiskolai Tanulmányi Verseny - a korábbi évekhez hasonlóan - ebben a két évben is három kategóriában került megrendezésre. Külön-külön csoportban versenyeztek a szakiskolák tanulói, az általános-, valamint az emelt szintű fizikaoktatásban részesülő diákok. Mind a három csoport részére három fordulóból álltak a versenyek. Az első két forduló során elméleti problémákat kellett megoldaniuk a versenyzőknek, míg a harmadik fordulóban mérési feladatokkal kellett megbirkózniuk. A harmadik fordulóban az első két forduló legjobbjai mérték össze tudásukat és ügyességüket.
A BME Fizikai Intézet az emelt szintű fizikaoktatásban részesülő diákok (harmadik kategória) versenyének harmadik fordulóit rendezte. A versenyeknek ebben a fordulójában húsz-húsz fiatal vett részt. Közleményünkben ezekről a 2002-ben és 2003-ban lezajlott versenyekről számolunk be. Intézetünk 1994 óta vesz részt a versenyek lebonyolításában. A korábbi versenyekről évente rendszeresen beszámoltunk a Fizika Módszertani Lapokban.
Dolgozatunkban bemutatjuk a versenyfordulók kezdetekor kiadott írásos anyagokat úgy, ahogy a versenyzők megkapták. Ezen anyagok segítségével akartuk megismertetni a versenyzőket a megoldandó feladatokkal és a feladatok megoldásához rendelkezésükre álló eszközökkel. A kiadott írásos anyagok bemutatása után vázoljuk a kitűzött feladatok megoldásának módját, majd beszámolunk a verseny közben és az értékelés során szerzett tapasztalatokról, a versenyzők eredményeiről, végül köszönetet mondunk mindazoknak, akik közreműködtek a versenyek előkészítésében vagy lebonyolításában.
A versenyzők részére 2002-ben kiadott írásos anyag
Feladat a Fizika OKTV harmadik fordulójára, a harmadik kategória részére
Dominósor eldőlésének vizsgálata
A magyar televízió az utóbbi időkben kétszer is sugárzott műsort dominósorok feldőléséről. 1999 novemberében a hollandiai Zuidlarenben 3,112 millió dominót döntöttek fel egy Guinness-rekordkísérlet során. 2000 novemberében egy újabb rekord felállításakor 3,750 millió dominó látványos feldőlésében gyönyörködhettek a nézők.
Ha egy nagyobb számú dominóból álló összeállítás feldőlését szeretnénk megtervezni, és a feldőlés során események időbeli egybeesését is tervezzük, ismernünk kell a dominók feldőlésének törvényszerűségeit.
A feladat
A verseny során azt kell megvizsgálnia a rendelkezésére álló eszközök segítségével, hogy hogyan viselkedik egy egymástól azonos távolságban felállított dominókból álló sor, eldőlés közben. Milyen tényezők, és milyen mértékben befolyásolják a sor dőlésének folyamatát?
Legalább elérendő cél, hogy vizsgálatai eredményeként egy képzeletbeli dominó döntési terv elkészítéséhez arra tudjon válaszolni, hogy a rendelkezésére álló dominókból, különböző, tetszőlegesen megválasztott dominótávolság (például: mindegyik dominó 15 mm, vagy valami más távolságra van egymástól) esetén mennyi idő alatt dől el egy egyenes sor adott szakasza (például egy hosszabb dominósor 2. és 3. méter közötti szakasza).
Gondolja végig, hogy milyen méréseket kell elvégeznie, végezze el a szükséges méréseket, mérési adatait dolgozza fel, és értékelje kapott eredményeit.
A rendelkezésére álló anyagok és eszközök
35 db dominó
1 db pozdorjalemez milliméterpapír borítással
2 db fénykapu, időmérő elektronikával (alkalmazásukat lásd később)
1 db tápegység az időmérő elektronikához
2 db derékszögű vonalzó
1 db mérőszalag milliméterpapír
A fénykapuk használata
A két darab fénykapu közül az egyik az indító (fehér színű), a másik a leállító (piros színű). Ha az indító kapu fényútját valami megszakítja, az elektronika elkezdi az időt mérni, és mindaddig mér, míg a másik kapu fényútja meg nem szakad. A kapukon a fényforrás és az érzékelő magassága állítható, figyeljen arra, hogy a két elem azonos magasságban legyen. Indítás előtt az elektronikát az előlapján található gombbal nullázni kell. A mért idő számok formájában, ezred másodpercekben leolvasható az elektronika kijelzőjéről. Az elektronika működéséhez 4,5 V-os feszültség szükséges, ezt a tápegység biztosítja.
|
|
|
|
A kiadott "További tudnivalók" tájékoztatott a verseny időtartamáról, a használható segédeszközökről, javaslatot tartalmazott az elkészítendő jegyzőkönyv tartalmára, megadta az eszközök esetleges meghibásodása esetén szükséges teendőket, és felhívta a figyelmet a gondos mérés fontosságára. Egy dőlő dominósorról készült felvételt mutat az 1. ábra.
A 2002. évi feladat megoldása
A feladat megoldása két részre bontható: meg kell állapítani, hogy a dominósor elején, a dőlés kezdeténél hogyan alakul a dőlési sebesség, majd ezután következnek az állandósult dőlési sebességre vonatkozó vizsgálatok.
A feladat megfogalmazásakor úgy gondoltuk, hogy nem hívjuk fel a versenyzők figyelmét az eldőlő sor elején lejátszódó folyamatokra. Ha ezt megtesszük, a versenyt az nyerte volna meg, aki a leggyorsabban tudta volna a dominósorokat felállítani, hiszen gondolkozás nélkül, csak a sorok felállítását és az eldőléshez szükséges idő mérését kellett volna elvégezni.
Belátható, hogy az eldőlő sor eleje másként viselkedik, mint egy távolabbi szakasz. A sor elején várhatóan változik az eldőlési sebesség, s egy tranziens viselkedés játszódik le, míg a távolabbi szakaszokon a dőlési sebesség már állandósul.
A sor eldőlésekor a második dominónak egy dől neki, a harmadiknak már kettő, és így tovább. A dőlési sebesség várhatóan addig változik, míg az eldőlő dominókból kialakul egy olyan szakasz, amelynek utolsó tagja (ha balról jobbra döntjük a sort, a bal szélső elem) már fekszik a következőn, míg az első (a szakasz jobb szélén lévő elem) még éppen áll. Ettől kezdve a dőlési sebesség állandó, és a részben eldőlt dominókból álló szakasz ezzel a sebességgel mozog előre.
Itt megjegyezzük, hogy a "dőlési sebesség"-et úgy határozzuk meg, hogy két megfelelő dominósík távolságát osztjuk a síkok azonos helyzetéhez tartozó időpontok különbségével. Tehát nem vizsgáljuk egy-egy dominó sebességének változását a dőlés kezdetétől a nyugalmi helyzet kialakulásáig. Azt, hogy az állandósult sebesség a sor elején mekkora szakaszon alakul ki, szerkesztéssel és méréssel is megvizsgáltuk.
A tranziens jelenség lezajlásával kapcsolatban elmondottaknak megfelelő szerkesztésre mutat példát a
2. ábra, ahol az adott méretű (60![]() 30
30![]() 6 mm-es) dominók megfelelő síkjai 30, illetve 50 mm-re helyezkednek el egymástól.
6 mm-es) dominók megfelelő síkjai 30, illetve 50 mm-re helyezkednek el egymástól.
A szerkesztésből (a már teljesen eldőlt és a még függőlegesen álló dominó távolságából) az látszik, hogy az adott méretű dominókkal, a különböző dominótávolságok esetén elvégzett szerkesztések hasonló eredményt adnak. Ilyen méretű elemek alkalmazásakor az állandósult sebesség kialakulása 20-21 cm-es szakasz után várható.
A sorok elején lejátszódó tranziens folyamatot méréssel úgy vizsgáltuk, hogy a fénykapu indító érzékelőjét a második dominónak a dőlés irányába eső második határoló síkjával, a leállító érzékelőt a harmadik, a negyedik stb. dominó második határoló síkjával helyeztük egy vonalba. Az érzékelőket azonos magasságra - a dominók tetejéhez- állítottuk, hogy a vizsgált síkok azonos helyzete indítsa, illetve állítsa le az időmérést. Az érzékelők elhelyezését a 3. ábra mutatja. Az előbb elmondottak szerint a dőlési sebességet a két vizsgált sík egymástól való s távolságának és az érzékelők által mért időtartamnak a hányadosa adja, azaz:
![]()
![]()
ahol n a figyelembe vett dominók száma.
3. ábra. Az érzékelők elhelyezése a dominósoron.
A sor dőlését az első dominó óvatos döntésével indítottuk úgy, hogy igyekeztünk azt az egyensúlyi helyzetén kissé túlvinni és ott elengedni, magára hagyni. 60![]() 30
30![]() 6 mm-es dominókkal végzett mérés eredményeit tünteti fel a
4.a ábra, amikor s = 30 mm volt. A
4.b ábra az s = 40 mm mellett végzett mérés eredményeit jeleníti meg.
6 mm-es dominókkal végzett mérés eredményeit tünteti fel a
4.a ábra, amikor s = 30 mm volt. A
4.b ábra az s = 40 mm mellett végzett mérés eredményeit jeleníti meg.
A kapott grafikonok alapján a következőket állapíthatjuk meg:
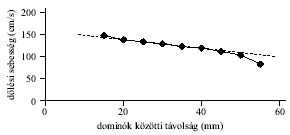
5. ábra. A dominósor állandósult dőlési sebessége a dominók közötti távolság függvényében.
A grafikonok segítségével az állandósult sebességek is meghatározhatók a lineáris szakasz meredekségéből. Az s = 30 mm esetén a grafikon lineáris szakaszára illesztett egyenes meredeksége, a dominósor állandósult dőlési sebessége: 126,2 cm/s-nak, míg s = 40 mm-nél 116,3 cm/s-nak adódott. Ha a dominósor egyes elemei közötti távolságot 9 mm-től kezdődően (amikor a vizsgált síkok közötti távolság: s = 9+6 = 15 mm) 5 milliméterenként szeretnénk növelni 49 mm-ig (ekkor s = 55 mm), és az előbbi módon felvett grafikonokat akarjuk felhasználni az állandósult sebesség meghatározásához, igen sok mérést kellene elvégezni. Erre a négy órás idő nem elegendő. Ezért célszerű úgy eljárni, hogy olyan távolságon mérjük az eldőléshez szükséges időt, amely már olyan messze van a sor elejétől, hogy itt már biztosan állandósult a sebesség. Ezért az időkapu indító érzékelőjét a felállított sor elejétől legalább 21 cm-re, és a leállító érzékelőt lehetőleg minél messzebbre helyeztük. A méréshez használt elrendezés egyezik a 3. ábrán bemutatottal. A dőlés indítását a már ismertetett módon végeztük. A mérések eredményét az 1. táblázatban tüntettük fel, ahol az első oszlopban a korábban értelmezett s értékeket tüntettük fel. A "Mért idők"-et több (három-öt) mérés számtani közepeként kaptuk.
A méréseket azért kezdtük az s = 15 mm-nél, mert kisebb s értékek esetén az "indító" dominó csak nekidől a következő elemnek, és nem indítja el a sor dőlését. A dominók közötti távolság növekedésével a még álló dominókra a nekik dőlő dominók egyre nagyobb sebességgel érkeznek. A mérés egyre érzékenyebb arra, hogy a felállított elemek mennyire párhuzamosak egymással. A dominótávolságok növekedésével növekszik a mérési adatok szórása. Hibás felállítás esetén egyes elemek valósággal "kirepültek" a sorból. A dominók mérete: 60![]() 30
30![]() 6 mm.
6 mm.
Az 1. táblázat adatainak felhasználásával készítettük el az 5. ábrát, ahol az s távolság függvényében tüntettük fel az állandósult dőlési sebességet. Az ábra alapján azt állapíthatjuk meg, hogy a sebesség egy kezdeti, viszonylag nagyobb érték után egy darabig közel lineárisan, majd egyre erősebben csökken. A kitűzött feladatot a versenyen használt dominóktól eltérő méretű mintákkal is elvégeztük, és a sebesség-dominótávolság kapcsolat mindegyik esetben az 5. ábrán látható jelleget mutatta.
A versennyel kapcsolatos megjegyzések, eredmények
Ebben az évben - a korábbi évekhez viszonyítva - az elméleti fordulók után szélesebb tartományban változott a versenyzők teljesítménye. A 3. fordulóba bekerült versenyzők teljesítménye az első két forduló eredményeit figyelembe véve 75% és 100% közé esett. Két teljesítményérték volt, amelyet több versenyző ért el: öt-öt fő teljesített 93,3, illetve 75%-ra.
A harmadik forduló során a versenyzők teljesítményének megállapításánál értékeltük a tranziens folyamat vizsgálatát, a dőlési sebesség meghatározását, a hibaszámítást, és néhány pontot adtunk a kiadott feladatok között nem szereplő, de azt kiegészítő mérések elvégzéséért.
A tranziens viselkedés kérdésével két versenyző egyáltalán nem foglalkozott, kilencen minden vizsgálat és magyarázat nélkül különböző számú - általuk "előtagnak" vagy "felvezető dominónak" nevezett - dominót alkalmaztak, és mindössze heten végeztek valamilyen vizsgálatot arra vonatkozóan, hogy a sor elején hogyan alakul a dőlési sebesség.
Azok, akik a tranziens jelenség kérdésével egyáltalán nem foglalkoztak, a dőlési sebességet mindig a sornak a második dominóval kezdődő szakaszán mérték. Így mérési eredményeik nem az állandósult sebességet adták meg.
Az "előtag" vagy "felvezető dominó" azt jelentette, hogy a dőlési sebességet csak a dominósor elején lévő néhány dominó utáni szakaszon mérték. Az "előtagok" száma "néhány"-tól 15-ig változott. Volt olyan versenyző is, aki mindig felállította a rendelkezésére álló 35 dominót, és a sebességet csak a sor végén mérte.
Azok közül, akik vizsgálatokat végeztek az állandósult sebesség kialakulására vonatkozóan, néhányan nem a dőlési sebesség változását vizsgálták a sor elején, hanem azt mérték ki, hogy adott számú dominó dőlési ideje hány "előtag" után állandósul. Állandó számú (10- 15 db) dominóból álló szakasz feldőlésének idejét mérték, változó számú (2, 3, 4, … db) "előtag" alkalmazása esetén.
A versenyzők viszonylag kevés (négy-öt) különböző dominótávolság esetén határozták meg az állandósult sebességet, egy-egy mérést rendszerint háromszor megismételve. A sebesség és a dominótávolság közötti kapcsolatot lineárisnak találták.
Néhányan foglalkoztak a dőlés indításának kérdésével is. Azt vizsgálták, hogy az első dominó meglökése hogyan befolyásolja a sor dőlési sebességét. Ők azt találták, hogy az első elem "elhanyagolható kezdősebességétől" az "igazán nagy impulzusig" az indítás sebessége "nem igazán befolyásolja" a 11. és 16. dominó közötti szakasz dőlési sebességét.
A versenyzők nagy része végzett hibaszámítást. A mérési eredmények relatív hibáját határozták meg.
Többen végeztek vizsgálatokat "elfektetett" (60 mm-es oldalra állított) dominókkal is. Őket néhány pluszponttal jutalmaztuk.
Az érzékelők magassága állítható volt. A legtöbben - helyesen - azonos magasságba állították az indító és a leállító érzékelőt, és a 3. ábrának megfelelően állították be őket. Akik ettől eltértek, azok különböző magasságban hagyták az érzékelőket, vagy úgy állították be őket, hogy az elfekvő dominókat érzékeljék.
Kereskedelmi forgalomban vásárolt dominókkal sajnos nem kaptunk megbízható eredményeket. Ezért a verseny céljára 6 mm-es plexilemezből csináltattuk a dominókat. A precízkivitelez és eredményeként a mérések reprodukálható eredményeket adtak. A dominók oldallapjait matt fekete festékkel festettük le, mert az átlátsz ó plexi nem zárta az érzékelők előtt a fényutat. Az idő mérésére szolgáló fénykapukat és a hozzájuk tartozó elektronikát magunk készítettük.
A dominósorok felállítása elég időigényes és bizonyos kézügyességet igénylő feladat. A felállítás közben egyetlen elem véletlen meglökése elég ahhoz, hogy az egész, addig felállított sor azonnal eldőljön. Emiatt verseny közben gyakran hallottuk a versenyzők kifakadásait. Néhányan a mérési jegyzőkönyvben is megemlítették ezt a nehézséget.
A mérési forduló meglehetősen széthúzta a mezőnyt. A versenyzők teljesítménye a harmadik forduló során 100% és 33% közé esett. Az elméleti és a gyakorlati fordulók eredményeinek összesítése után a versenyzők teljesítménye 100% és 62% között mozgott. Az elméleti fordulók után az első tíz helyezett közül heten a végső sorrendben is az első tíz között voltak, a sorrend azonban némileg változott. A verseny után a résztvevők a feladatot könnyűnek minősítették.
Megjegyezzük, hogy eredetileg a kérdés összetettebb vizsgálatát terveztük. Szerettük volna a kitűzött feladatot különböző méretű dominókkal elvégeztetni. Magunk három különböző méretű dominóval végeztük el a méréseket. Sajnos azonban úgy láttuk, a négy órás idő ilyen feladat megoldására nem elegendő.
Az 2002. évi verseny első tíz helyezettje az összesített eredmények alapján
A versenyzők részére 2003-ban kiadott írásos anyag
Feladat a Fizika OKTV harmadik fordulójára, a harmadik kategória részére
Közegellenállási erő vizsgálata
Feladat
A feladat megoldásához rendelkezésére álló anyagok és eszközök
2 db belül üres hengeres minta (tömegüket megmértük, az eredményeket a mérőhelyen megtalálja), menetes kupakkal, gumitömítéssel, 0,2 mm vastag alumíniumlemezből készült vezető szárnyakkal,
8 db csapágygolyó (1 db tömege 8,95 g),
1 db kis mágnes, piros műanyag foglalatban, a vízbe ejtett minta kiszedéséhez,
1 db sárgaréz függőző, a függőleges irány kijelöléséhez,
1 db tolómérő,
1 db csipesz,
1 db mérőszalag,
1 db Bunsen-állvány,
3 db Bunsen-dió,
1 db Bunsen-fogó,
1 db üvegcső vízzel, a tetején sapkával, a sapka közepén furattal, alul lezárva,
1 db mérőpohár vízzel,
2 db fénykapu, időmérő elektronikával (alkalmazásukat az előző évi feladattal kapcsolatban már ismertettük),
cérna,
milliméterpapír,
karton lapocska, a fényút megszakításához.
A "További tudnivalók" címmel a 2002 évihez hasonló információkat adtunk a versenyzőknek.
A hengeres minták a 6. ábrán láthatók, a mérőhelyen elhelyezett néhány eszközzel.
A 2003. évi feladat megoldása
Az állandósult állapot kialakulásának vizsgálata esés közben
Először megvizsgáltuk azt, hogy mekkora úton áll be az állandósult állapot, amelytől kezdve a minta már állandó sebességgel mozog. Az állandó sebesség azt jelzi, hogy a minta súlya, a mintára ható felhajtóerő és a közegellenállási erő egyensúlyban van. A leghosszabb úton és a legnagyobb sebesség mellett, a legnehezebb minta

6. ábra. Hengeres minták a mérőhelyen elhelyezett néhány eszközzel.
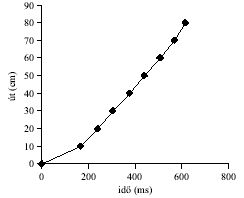
7. ábra. Az eső minta út-idő
grafikonja.
esetén alakul ki az egyensúlyi helyzet. Ezért ezt a vizsgálatot a csapágygolyókkal (8 db) megtöltött hosszabb mintával végeztük úgy, hogy felvettük a test út-idő grafikonját. A többi lehetséges esetben (a rövidebb minta vagy kevesebb csapágygolyó alkalmazásakor) rövidebb úton áll be az egyensúlyi helyzet. Az út-idő kapcsolat megállapításához a mintát függőleges üvegcsőben lévő vízbe ejtettük. A megmért, illetve megadott méretek: A vízzel töltött üvegcső belső átmérője: D = 46 mm, a hossza: 125 cm. A hosszabb hengeres minta átmérője: d = 16 mm, hossza: h = 130 mm, tömege: m0 = 19,8 g. A négy darab alumínium vezető szárny vastagsága: sz = 0,2 mm, magassága: l = 12 mm és hossza: h* = 125 mm. 1 db csapágygolyó tömege: mg = 8,95 g. A mintát csipesszel megfogva, teljesen vízbe merítettük, és függőleges helyzetben a cső közepéről indítottuk. A gondos indítás az eredményes mérés feltétele! A minta kiszedése az üvegcső aljáról a cérnára erősített mágnes és a minta tetejébe süllyesztett acél csavar segítségével oldható meg. Az indító érzékelőt közvetlenül a már teljesen vízbe merülő minta alatt helyeztük el, a leállító érzékelőt pedig s = 10, 20, 30, … cm-rel lejjebb.

A mérési eredmények ~5-6%-os szórást mutattak, ami a minta függőlegestől eltérő mozgása során a fallal történő súrlódással indokolható. Ezért 10-10 esetben mértük az adott út megtételéhez szükséges időt, és a további munkához a mért idők közül a legrövidebbeket vettük figyelembe. Feltételeztük, hogy ezekben az esetekben a minta nem ért a falhoz, vagy a fal hatása elhanyagolható volt. A mért legrövidebb idők feltüntetésével készült a 7. ábra. Az ábráról megállapítható, hogy az állandósult állapot rövid szakaszon kialakul, és 20 cm út megtétele után a minta már biztosan állandó sebességgel mozog.
Ha az állandó sebességhez tartozó mérési pontokra egyenest illesztünk, az illesztett egyenes egyenlete (SI egységekben):
y = 1,54 x - 16,8
A mérési pontok jól illeszkednek az egyenesre, és a minta állandósult sebessége 1,54 m/s. A sebesség - közegellenállási erő kapcsolat megállapításának egyik módja lehetne a leírt kísérlet megismétlése 7, 6, … csapágygolyóval. Ez az eljárás azonban meglehetősen időigényes.
Rövidebb úton, kevesebb méréssel oldhatjuk meg a feladatot, ha az elvégzett mérés eredményére támaszkodva a további vizsgálatokat rögzített út megtételéhez szükséges idők mérésével végezzük. Az indító kaput a vízbe merített minta alsó éle alatt 25 cm-rel, a leállító kaput további 30 cm-rel lejjebb helyezzük el. Így a vizsgált minta állandó sebességű mozgásából mindig 30 cm-nyi szakaszt vizsgálunk.
További mérések a hosszabb mintával
A belül üres minta önmagában, vagy egy csapágygolyóval a belsejében nem süllyed el. Ezért a további vizsgálatokat 2, 3, …, 8 db golyóval megtöltött mintával végeztük. A különböző számú golyóval megtöltött minta a fenti módon meghatározott 30 cm utat a 2. táblázatban feltüntetett idők alatt tette meg.
Az esés sebességének kiszámításához most is 10-10 esetben mértük az időt, és itt is a legrövidebb időt vettük figyelembe, ezeket az időket a táblázatban bekereteztük. A mérési eredmények felhasználásával kiszámított sebességeket is feltüntettük a táblázatban. (Megállapítható, hogy a 8 csapágygolyóval terhelt minta most mért sebessége jó egyezésben van az út-idő grafikonra illesztett egyenes meredekségéből korábban meghatározott értékkel.)
A mérés során a mintának az üvegcsőhöz viszonyított sebességét határoztuk meg. Ezzel szemben a közegellenállási erő a minta és a víz egymáshoz képesti sebességétől függ!
Annak a csőnek a belső átmérője (D = 46 mm), amelyben a minta mozgását vizsgáljuk, összemérhető a minta átmérőjével átmérőjével (d = 16 mm). Ezért nem hanyagolhatjuk el, hogy a víz a minta mellett felfelé áramlik.
Ha A0 a cső, A1 a minta (a négy vezető szárnnyal) hossztengelyre merőleges metszetének a területe, v a minta korábban meghatározott esési sebessége, és a csőben a minta mellett felfelé áramló vízsebessége a csőhöz képest v*, akkor:
vA1 = v* (A0 - A1) .
A minta vízhez viszonyított sebessége pedig:
![]()
ahol a K korrekciós állandó értéke:
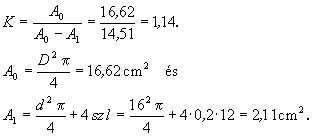
Egyensúly esetén (állandó sebességű mozgásnál) a mintára ható közegellenállási erőt (Fk ) a minta súlyának (G) és a mintára ható felhajtóerőnek (Ff ) a különbsége adja meg.
A felhajtóerő a hengerre:
![]()
A felhajtóerő a szárnyakra:
![]()
A hosszabb mintára ható felhajtóerő:
Ff = Ff h + Ff sz = 0,27 N.
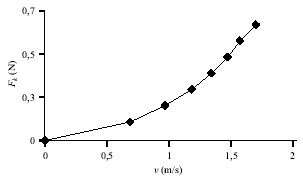
8. ábra Közegellenállási erő - sebesség függvény hosszabb minta esetén.
A minta tömege (![]() ), az üres minta tömegének (m0) és a golyók tömegének (nmg ) az összege.
), az üres minta tömegének (m0) és a golyók tömegének (nmg ) az összege.
A golyókkal terhelt minta súlya: G = (m0 + nmg ) g.
A közegellenállási erő: Fk = G - Ff .
Az így kapott eredmények a 3. táblázatban láthatók.
A mérési eredmények felhasználásával készült közegellenállási erő - sebesség kapcsolatot mutatja a 8. ábra.
A mérési pontok jól illeszkednek az Fk = 0,196x2 parabolára, tehát a vizsgált sebességtartományban a közegellenállási erő a sebesség négyzetével arányosnak tekinthető.
A közegellenállási erő - sebesség kapcsolatra ismert összefüggés:
![]()
ahol k az "alaki tényező", ![]() annak a közegnek a sűrűsége, amelyben a test mozog (most
annak a közegnek a sűrűsége, amelyben a test mozog (most ![]() ) A a test mozgásirányra merőleges legnagyobb keresztmetszete (jelen esetben: A1) és v a közeg és a test relatív sebessége (Kv).
) A a test mozgásirányra merőleges legnagyobb keresztmetszete (jelen esetben: A1) és v a közeg és a test relatív sebessége (Kv).
A mérési pontokra illesztett parabola egyenletéből és a közegellenállásra vonatkozó összefüggésből a keresett alaki tényező:
![]()

A mérési eredmények feldolgozásának egy másik lehetséges módja, hogy felrajzoljuk a sebesség (Kv) függvényében a közegellenállási erő négyzetgyökét ![]() . Így kaptuk a 9. ábrát. Ha a mérési pontokra egyenest illesztünk, az egyenes egyenlete:
. Így kaptuk a 9. ábrát. Ha a mérési pontokra egyenest illesztünk, az egyenes egyenlete:
![]()
Az egyenes egyenletének és a közegellenállásra vonatkozó egyenletnek az összevetéséből az alaki tényező:
![]()
Az ismertetett mérési eljárással és a fenti számítási módszert követve meghatároztuk a rövidebb minta alaki tényezőjét is. A minta adatai a következők voltak: átmérője: D = 16 mm, hossza: h = 6,9 cm, tömege: m0 = 10,46 g. A négy vezetőszárny vastagsága: sz = 0,2 mm, magassága: l = 12 mm és hossza: h* = 63 mm. A vizsgált minta alaki tényezőjének k = 1,29 adódott.

9. ábra. A közegellenállási erő négyzetgyöke a sebesség függvényében.
Az eredmények értékelése
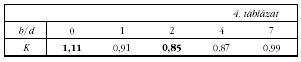
Henger esetén, ha az áramlás párhuzamos a tengellyel, az alaki tényező a henger hosszának (h) és átmérőjének (d) arányától a 4. táblázatban közölt módon függ (Grúber J., Blahó M.: Folyadékok mechanikája - Tankönyvkiadó, 1963, 286. o.):
A körlap 1,11 értékű alaki tényezője a henger hosszának növekedésével eleinte csökken, mert a homlokfelület keltette turbulenciát a felület mögötti test csökkenti. Az aránylag hosszú hengernél az áramlás irányával párhuzamos felületeken fellépő súrlódási ellenállás számottevő lesz, és ezért az alaki tényező növekszik. A középiskolákban használatos "Függvénytábla" a körlap és a tengellyel párhuzamos áramlásba helyezett henger legkisebb alaki tényezőjét adja meg. (A 4. táblázatban vastagított számokkal.)
Eredeti elképzelésünk az volt, hogy a versenyzők legalább három azonos átmérőjű és különböző hosszúságú minta segítségével vizsgálják meg az alaki tényező alakulását. Amikor a feladatot magunk megoldottuk, láttuk, hogy a verseny 4 órás időtartama nem elég az elképzelt program végrehajtásához. Ezért csak két eltérő hosszúságú mintával tűztük ki a feladatot.
Az elvégzett mérések eredményei jól mutatják a henger hosszának hatását az alaki tényezőre. A mérés segítségével kapott alaki tényező értékek lényegesen nagyobbak a 4. táblázatban szereplőknél. Ennek magyarázatát a vezérlő szárnyak felületén jelentkező súrlódási ellenállásban kereshetjük.
A versennyel kapcsolatos tapasztalatok
A versenyzők pontszámai az elméleti fordulók után 300 és 200 pont között oszlottak meg. Előfordult, hogy kéthárom versenyzőnek volt azonos pontszáma. A gyakorlati forduló eredményei széthúzták a mezőnyt. Itt a pontszámok 200 és 32 között változtak.
Az elméleti és a gyakorlati forduló eredményeit figyelembe véve az összesített pontszámok 480 és 244 között változtak. A korábbi versenyektől eltérően most a vidékiek voltak többségben.
A gyakorlati forduló alkalmával a következőket tapasztaltuk:
A 2003. évi verseny első tíz helyezettje az összesített eredmények alapján
Köszönetnyilvánítás
A verseny lebonyolításához szükséges anyagi hátteret az Országos Közoktatási Szolgáltató Intézmény biztosította. Ezt ezúton is köszönjük.
A verseny lebonyolításához szükséges mechanikai munkák a BME Kísérleti Fizika Tanszék műhelyében készültek. Az állványok, befogók, minták, függők stb. gyors és igényes elkészítéséért Berende László, Horváth Béla és Halász Tibor műszerészeket illeti köszönet.
A verseny lebonyolításához szükséges körülmények megteremtéséért - a mérőhelyek kialakításáért, a versenyzők kondíciójának megőrzéséhez felszolgált italok és szendvicsek beszerzésért és elkészítéséért stb. - Burján Lászlónénak, Kovács Ferencnének, Gál Bélánénak és Mezey Miklósnak mondunk köszönetet. Reméljük, hogy munkájuk eredményeként a versenyzők jól érezték magukat a verseny alatt.
A feladat kitűzésével, a verseny lebonyolításával kapcsolatos hasznos tanácsaiért Tóth Andrásnak és Kálmán Péternek mondunk köszönetet.
A versennyel kapcsolatos adminisztrációs és gazdasági ügyek intézéséért Köves Endrénét és Gál Bélánét illeti köszönet.
Elismerés és köszönet illeti mindazokat (szülőket, tanárokat, barátokat stb.), akik segítették a versenyzők munkáját és ezzel hozzájárultak a verseny sikeréhez.