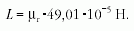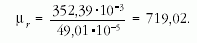Fizikai Szemle 2004/11. 390.o.
A FIZIKA ORSZÁGOS KÖZÉPISKOLAI TANULMÁNYI VERSENY
HARMADIK FORDULÓJA A HARMADIK KATEGÓRIA RÉSZÉRE
- 2004
Vannay László, Fülöp Ferenc, Máthé József, Nagy Tamás, Vankó Péter
Budapesti Műszaki és Gazdaságtudományi Egyetem, Természettudományi Kar
Fizikai Intézet, Kísérleti Fizika Tanszék
A Fizika Országos Középiskolai Tanulmányi Verseny - a
korábbi évekhez hasonlóan - ebben az évben is három kategóriában
került megrendezésre. Külön-külön csoportban
versenyeztek a szakiskolák tanulói, az általános-, valamint
az emelt szintű fizikaoktatásban részesülő diákok.
Mind a három csoport részére három fordulóból állt a
verseny. Az első két forduló során elméleti problémákat
kellett megoldaniuk a versenyzőknek, míg a harmadik
fordulóban mérési feladatokkal kellett megbirkózniuk. A
harmadikfordulóban az első két forduló legjobbjai mérték
össze tudásukat és ügyességüket.
A BME Fizikai Intézet az emelt szintű fizikaoktatásban
részesülő diákok (harmadik kategória) versenyének harmadik fordulóját
rendezte. A versenynek ebben a fordulójában
tizenkilenc fiatal vett részt. Közleményünkben,
erről a versenyről számolunk be.
Dolgozatunkban bemutatjuk a versenyforduló kezdetekor
kiadott írásos anyagot úgy, ahogy a versenyzők
megkapták. Ezen anyag segítségével akartuk megismertetni
a versenyzőket a megoldandó feladattal, és a feladat
megoldásához rendelkezésükre álló eszközökkel. A kiadott
írásos anyagok bemutatása után vázoljuk a kitűzött
feladatok megoldásának módját, majd beszámolunk a
verseny közben és az értékelés során szerzett tapasztalatokról,
és a versenyzők eredményeiről, végül köszönetet
mondunk mindazoknak, akik közreműködtek a verseny
előkészítésében, vagy lebonyolításában.
A feladat
Vasmag relatív permeabilitásának meghatározása, valamint
elmozdulásérzékelők összeállítása, hitelesítése és
alkalmazása.
- Relatív permeabilitás mérése
3 V-os, tápfeszültséget alkalmazva, határozza meg a
mérőhelyen található transzformátorlemezek anyagának
az adott körülmények között érvényes relatív permeabilitását.
-
Elmozdulásérzékelők összeállítása, hitelesítése
és alkalmazása
- A rendelkezésére álló elemekből állítson össze
olyan eszközt, amelynek valamely mérhető jellemzője
egy elmozdulástól függ. Az összeállítással egy elmozdulás
(távolság) mérésére alkalmas érzékelőt kap. Rajzolja
le az érzékelő vázlatát, és röviden ismertesse működését.
- Hitelesítse az összeállított érzékelőt, azaz határozza
meg a mérhető jellemző és az elmozdulás közötti kapcsolatot.
- A hitelesítés során kapott mérési eredményeit adja
meg táblázatban, és tüntesse fel grafikonon is.
- A hitelesített eszközzel mérje meg a kiadott zománcozott
rézhuzal átmérőjét.
- A rendelkezésére álló elemekből többfajta elmozdulásérzékelő
állítható össze. Lehetőleg állítson össze Ön
is többfélét, és végezze el ezek hitelesítését is, majd ezekkel
is mérje meg a kiadott zománcozott rézhuzal átmérőjét.
- Röviden jellemezze az összeállított eszközöket.
Az értékelés megkönnyítése érdekében a mérésekhez
mindig 3 V-os tápfeszültséget alkalmazzon, és ha mérése
valamely részében állandó frekvenciát akar alkalmazni,
akkor 50 Hz-es frekvenciát használjon!
A verseny során végzett munkájáról készítsen részletes
jegyzőkönyvet!
A feladat megoldásához rendelkezésre álló anyagok
és eszközök:
- 2 db tekercs (mindegyiken 600 menet) végeiken
banándugós huzallal
- 26 db U alakú vasmag lemez
- 26 db I alakú vasmag lemez
- 2 db csavaranyával
- 1 db HAMEG gyártmányú hanggenerátor-teljesítményerősítővel
(a használatával kapcsolatos tudnivalókat
a mérőhelyen megtalálja)
- 1 db HAMEG gyártmányú multiméter (ismertetését
a mérőhelyen megtalálja)
- 1 db "univerzális kéziműszer" (a használatával kapcsolatos
tudnivalókat a mérőhelyen megtalálja)
- 1 db plexidoboz, belsejében kondenzátorral, továbbá ellenállással, banánhüvelyes kivezetésekkel,
(a kondenzátor kapacitásának értékét a doboz
oldalán feltüntettük)
- 10 db 0,2 mm vastag műanyaglapocska
- 1-1 db 1, 2, 4 és 5 mm vastag műanyaglapocska
- Csavarhúzó és fogó
- Mérőzsinórok, banándugóval és csatlakozó kábelek
a hanggenerátorhoz és az erősítőhöz
- Milliméterpapír szükség szerint
- Az ismeretlen átmérőjű zománcozott rézhuzal
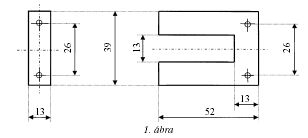
A vasmaglemezek vastagsága 0,5 mm, és további
méreteik az 1. ábráról leolvashatók. A lemezek felületkezeltek,
így az örvényáramok kialakulásának megakadályozása
miatt külön szigetelést nem igényelnek.
Megjegyzések
- Ha a kiadott műszerek használatával kapcsolatban
problémái jelentkeznek, forduljon a felügyelő tanárokhoz.
- Ha munkája közben rendellenességet tapasztal,
azonnal jelentse a felügyelő tanároknak.
- Tartsa be a balesetvédelmi előírásokat! Vigyázzon
saját magára és az eszközök épségére!
A feladat megoldása
Az A feladat megoldásához a 26 db U alakú lemezből
összeállított vasmagra ráhúztuk az egyik tekercset, majd
az összefogott 26 db I alakú lemez felhasználásával zárttá
tettük a vasmagot.
A zárt vasmagos tekercs önindukciós együtthatója méréssel
és számítással is meghatározható. A két eredmény
összevetéséből megkapjuk a transzformátorlemezek relatív
permeabilitásának értékét.
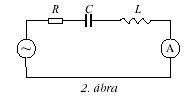
Méréssel a tekercs önindukciós együtthatója - a rendelkezésre
álló elemek felhasználásával - soros rezgőkörrel
határozható meg legegyszerűbben. Az alkalmazott
kapcsolást a 2. ábra mutatja, ahol C = 4,36 µF.
Ismeretes, hogy a soros rezgőkör áram a rezonancia
esetén éri el a legnagyobb értékét. Rezonancia akkor jön
létre, ha:
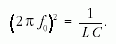
Ha az összeállított áramkörben állandó (3 V-os)
generátor feszültség mellett, a frekvencia változtatásával, az áramot
mérve megkeressük a rezonanciafrekvenciát, 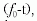 ,
akkor a kondenzátor kapacitását (C) ismerve meghatározhatjuk
a tekercs önindukciós együtthatóját (L ).
,
akkor a kondenzátor kapacitását (C) ismerve meghatározhatjuk
a tekercs önindukciós együtthatóját (L ).
Öt mérési eredmény átlagát véve azt találtuk, hogy a
rezonanciafrekvencia: 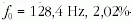 -os hibával. A
mérési eredmények felhasználásával a zárt vasmagos
tekercs önindukciós együtthatója:
-os hibával. A
mérési eredmények felhasználásával a zárt vasmagos
tekercs önindukciós együtthatója:
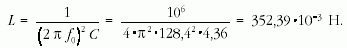
Számítással a tekercs önindukciós együtthatóját az alábbi
összefüggés felhasználásával határozhatjuk meg:
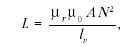
ahol µr keresett relatív permeabilitás, 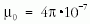 Vs/Am a vákuum permeabilitása, A a vaskeresztmetszet
(a lemezekméretéből meghatározhatóan 1,3 × 1,3 cm2), N
a tekercs menetszáma és lv a "közepes vashossz" (a lemezek méreteiből
Vs/Am a vákuum permeabilitása, A a vaskeresztmetszet
(a lemezekméretéből meghatározhatóan 1,3 × 1,3 cm2), N
a tekercs menetszáma és lv a "közepes vashossz" (a lemezek méreteiből
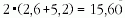 cm).
Az adatok felhasználásával:
cm).
Az adatok felhasználásával:
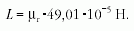
A méréssel és a számítással kapott eredményeket összevetve:
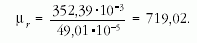
A feladat B részének megoldására két lehetőség kínálkozik.
Az egyik esetben egy tekercset helyezünk el a lemezekből
kialakított vasmagon, és a tekerccsel kialakított
soros rezgőkör rezonanciafrekvenciáját vagy a tekercs
önindukciós együtthatóját (esetleg impedanciáját) vizsgáljuk a
vasmag mágneses ellenállásánakfüggvényében.
A másik esetben két tekercset helyezünk el a vasmagon
és az így létrejött transzformátornak állandó primer
feszültség (3 V) mellett a szekunder feszültségét, vagy az
áttételét vizsgáljuk a vasmag mágneses ellenállásának
függvényében.
A vasmag mágneses ellenállása elsősorban a 3. ábrán
bemutatott módon változtatható. Az I alakú lemezekből
kialakított vasmag részt távolítva a tekercseket kitöltő U
alakú lemezektől, a mágneses körben lévő légrés méretének változtatásával
módosítható a mágneses ellenállás.
De változtatható a mágneses ellenállás az I alakú lemezekből
álló résznek az U alakú lemezeken történő elcsúsztatásával
is.
Látható volt, hogy a megmérendő drótvastagság valamivel
nagyobb mint 1 mm. Tehát érzékelőnkkel ilyen
nagyságrendű távolságot kell megmérnünk.
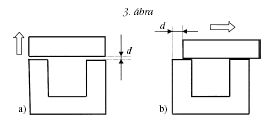
A szóba jöhető összeállítások jellemzőit kimérve, azt
lehet megállapítani, hogy a mágneses ellenállásnak a 3.b
ábra szerinti változtatásával megfelelő pontossággal csak
nagyobb, 4-8 mm-es távolságok mérhetők. Ezért a
továbbiakban csak a 3.a ábra szerinti összeállításokon végzett
méréseink eredményeit közöljük.
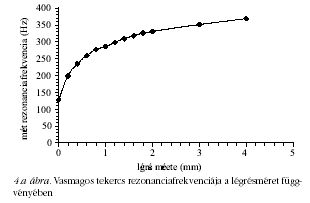
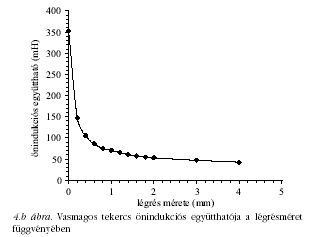
A vasmagon elhelyezett tekerccsel kialakított soros
rezgőkör rezonanciafrekvenciáját, illetve ennek ismeretében
a tekercs önindukciós együtthatóját a légrés 0,2 mm-es
lépésekben történő változtatása közben mértük. A
légrés méretét az erre a célra kiadott műanyag lapocskák
felhasználásával változtattuk. Minden légrésméretnél öt-öt
mérést végeztünk és a kapott eredmények számtani
közepét vettük figyelembe. (A mérések hibája nem volt
nagyobb, mint 2%.) Mérési eredményeink felhasználásával
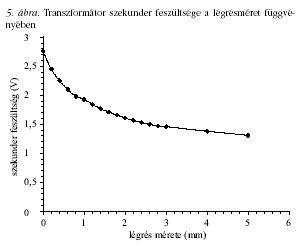
készült a 4. ábra.
A két tekercs és a vasmag segítségével kialakított
transzformátor viselkedését 3 V-os primer feszültséget
alkalmazva, a légrést 0,2 mm-es lépésekkel változtatva
vizsgáltuk. Egy adott légrésméret mellett a szekunder
feszültséget öt-öt alkalommal mértük meg, és az így kapott
értékek számtani közepét vettük figyelembe. (A
mérés hibája kisebb volt, mint 0,5%.) Mérési eredményeinkfelhasználásával
készült az 5. ábra.
A mérési eredményeket feltüntető ábrák - "hitelesítési
görbék" - felhasználásával lehet megmérni a kiadott
zománcozott huzal átmérőjét. A légrés méretét a mérendő
mintával állítjuk be, majd megmérjük az érzékelő kiválasztott
jellemzőjét (a soros kör rezonanciafrekvenciáját,
a tekercs önindukciós együtthatóját, vagy a transzformátor
szekunder feszültségét). A kiválasztott jellemző
értékének ismeretében a grafikonokról leolvasható
a minta mérete. A kiadott zománcozott huzal átmérője:
D = 1,24 mm volt.
A felrajzolt grafikonok azt mutatják, hogy a kialakított
érzékelők 2-3 mm-ig jól használhatók.
A versenymunkákkal kapcsolatos tapasztalatok
A vasmag relatív permeabilitását a legtöbben a középiskolákban
használatos Függvénytáblában található, a tekercs
önindukciós együtthatóját megadó képlet felhasználásával
határozták meg. Megmérték a légmagos és az
I alakú (néhányan az U alakú) vasmag lemezekkel kitöltött
tekercs önindukciós együtthatóját, majd a két érték
hányadosát véve számították ki a lemezek anyagának relatív
permeabilitását. Az így kapott eredmények 4 és 5
körül változtak.
A versenyzők zöme nem vette figyelembe, hogy az
általuk használt összefüggés milyen feltételek mellett
alkalmazható.
Nem tűnt fel senkinek sem, hogy a Függvénytábla az
indukció függvényében 3000-től 64-ig változó értéket ad
meg a transzformátorlemezek relatív permeabilitására.
Akadt olyan versenyző is, aki eltérő értéket várt az I és
az U alakú lemezek permeabilitására. Néhány versenyző
a tekercsbe helyezett vasmaglemezek számának változtatásától
várta a relatív permeabilitás módosulását.
Két versenyző volt, aki - helyesen - teljesen zárt vasmaggal
végezte vizsgálatait.
Az elmozdulásérzékelő kialakítására és hitelesítésére
majdnem mindenkinek volt jól használható ötlete. Észrevették
azt, hogy a vasmagos tekercs önindukciós együtthatója
és impedanciája, a transzformátor áttétele függ a
légrés méretétől.
Az önindukciós együtthatót soros rezgőkör segítségével
vizsgálták. A tekercs impedanciáját az Ohm-törvény
segítségével állapították meg, áram és feszültség mérésével.
Sajnos sokan „ideális” tekerccsel számoltak, és nem
vették figyelembe az impedancia valós részét, az ohmos
ellenállását. A versenyzők zöme nem vette figyelembe, hogy az
általuk használt összefüggés milyen feltételek mellett
alkalmazható.
Többen készítettek elmozdulásérzékelőt úgy, hogy a
tekercsből kihúzták a vasmagot és e közben mérték a
tekercs önindukciós együtthatójának, vagy az impedanciájának
a változását. Ennél a megoldásnál használtak
I és Ualakú lemezekből készített vasmagot is.
A jegyzőkönyvek értékelése alapján valószínűsíthető,
hogy a versenyzők nagy része nem volt tisztába azzal,
hogy a relatív permeabilitás a mágneses tértől (a mágneses
térerősségtől, illetve az indukciótól) és az anyagtól
függő jellemző.
Az elméleti fordulók után a versenyzők pontszáma 250
és 295 között változott. A harmadik forduló "széthúzta" a
mezőnyt, és néhány esetben jelentősen módosította a
sorrendet. A gyakorlati forduló jegyzőkönyveire adott
pontszámok 20-tól 200-ig változtak.
Az elméleti és a gyakorlati fordulókon elért pontszámok
összesítése után a pontszámok 280 és 465 között
változtak.
Az első tíz helyen öt vidéki és öt budapesti diák osztozott.
A résztvevők véleménye szerint nehéz volt a feladat.
Tekintettel arra, hogy akadt olyan diák, aki helyesen oldotta
meg a kitűzött feladatot, úgy gondoljuk, hogy az
megfelelő színvonalú volt. Egy versenyen, ahol sorrendet
kell megállapítani, nem lehet cél, hogy a feladatot minél
többen jól oldják meg.
Az összesített eredmények alapján
a 2004. évi verseny első tíz helyezettje
- VÍGH MÁTÉ a PTE Babits Mihály Gyakorló Gimnázium
és Szakközépiskola tanulója 465 ponttal
- KÓMÁR PÉTER, Fazekas Mihály Fővárosi Gyakorló
Általános Iskola és Gimnázium, 442
- MAZROA DÁNIEL, SZTE Ságvári Endre Gyakorló Gimnázium,
395
- Kanász N. Márton, Árpád Gimnázium (Bp.), 381
- . Németh Adrián, Fazekas M. Fővárosi Gyak. Ált. Isk.
és Gimn., 380
- Berczédi Balázs, Szilágyi Erzsébet Gimn. és Koll.
(Eger), 379
- Horváth Márton, Fazekas M. Fővárosi Gyak. Ált. Isk.
és Gimn., 376
- Kaposi Ambrus, Pannonhalmi Bencés Gimn. és Kollégium,
354
- Rácz Béla András, Fazekas M. Fővárosi Gyak. Ált.
Isk. és Gimn., 351
- Balázs Krisztián, PTE Babits M. Gyak. Gimn. és
Szakközép., 347
Köszönetnyilvánítás
A verseny lebonyolításához szükséges anyagi hátteret
az Országos Közoktatási Értékelési és Vizsgaközpont
biztosította. Ezt ezúton is köszönjük. A verseny lebonyolításához
szükséges eszközök elkészítéséért és a
megfelelő körülmények megteremtéséért Horváth Bélának,
Halász Tibornak, Kovács Ferencnének, Gál Bélánénak
és Mezey Miklósnak mondunk köszönetet. Reméljük,
hogy munkájuk eredményeként a versenyzők
jól érezték magukat a verseny alatt. A feladat kitűzésével,
a verseny lebonyolításával kapcsolatos hasznos tanácsaiért
Tóth Andrásnak és Kálmán Péternek mondunk
köszönetet. A versennyel kapcsolatos adminisztrációs
és gazdasági ügyek intézéséért Köves Endrénét és
Gál Bélánét illeti köszönet. Elismerés és köszönet illeti
mindazokat, (szülőket, tanárokat, barátokat stb.) akik
segítették a versenyzők munkáját és ezzel hozzájárultak
a verseny sikeréhez.

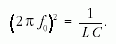
 ,
akkor a kondenzátor kapacitását (C) ismerve meghatározhatjuk
a tekercs önindukciós együtthatóját (L ).
,
akkor a kondenzátor kapacitását (C) ismerve meghatározhatjuk
a tekercs önindukciós együtthatóját (L ).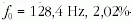 -os hibával. A
mérési eredmények felhasználásával a zárt vasmagos
tekercs önindukciós együtthatója:
-os hibával. A
mérési eredmények felhasználásával a zárt vasmagos
tekercs önindukciós együtthatója:
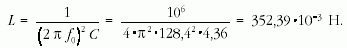
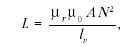
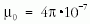 Vs/Am a vákuum permeabilitása, A a vaskeresztmetszet
(a lemezekméretéből meghatározhatóan 1,3 × 1,3 cm2), N
a tekercs menetszáma és lv a "közepes vashossz" (a lemezek méreteiből
Vs/Am a vákuum permeabilitása, A a vaskeresztmetszet
(a lemezekméretéből meghatározhatóan 1,3 × 1,3 cm2), N
a tekercs menetszáma és lv a "közepes vashossz" (a lemezek méreteiből
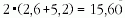 cm).
Az adatok felhasználásával:
cm).
Az adatok felhasználásával: