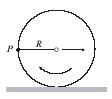
1. A jeges, vízszintes, egyenes úton egy személygépkocsi kereke úgy mozog, hogy a kerék tengelye t = 2 s alatt állandó sebességgel s₁ = 2,5 m hosszúságú utat tesz meg, a kerék kerületi pontjai pedig ezalatt egyenletes mozgással s₂ = 5 m hosszúságú ívet futnak be. A kerék sugara R = 25 cm
   1. Mekkora az ábrán megjelölt P pont úttesthez viszonyított sebessége és gyorsulása?
   2. Mekkora a P pont gyorsulásának pályamenti és a pályára merőleges komponense?
   3. Mekkora a kiszemelt P pont pályájának görbületi sugara ezen a helyen?

Koncz Károly, Pécs

2. Egyik végén zárt, vízszintes hengerben lévo, súrlódásmentesen mozgó dugattyú kétatomos ideális gázt zár el. A dugattyút a henger végével a dugattyúhoz és henger végéhez rögzített, L₀ = 50 cm hosszúságú, nyújtatlan húzó-nyomó rugó köti össze. A gáz kezdeti hőmérséklete T₀ = 560 K. A hengerben elzárt gázt lassan lehűtjük olyan T₁ hőmérsékletre, hogy a rugó hosszúsága L₁ = 25 cm-re csökken. A hűtés során a gáz Q₁ = 1060 J hőt ad le a környezetének. A hűtés után a gázt lassan olyan T₂ hőmérsékletre melegítjük fel, hogy a rugó hosszúsága L₂ = 75 cm legyen. Ismert, továbbá hogy a Kelvin-skálán mért hőmérsékletek aránya T₂ : T₁ = 4 : 1.
   1. Határozzuk meg T₁ és T₂ értékét!
   2. Mennyi hot kell közölni gázzal azon folyamat során, amikor a rugó hosszúsága L₀-ról L₂-re növekszik?

(Kotek László, Pécs)

3. Egy enyhe lejtésű betonúton fel kell juttatnunk egy nagy ládát és egy hordót. Van egy jól olajozott targoncánk, amelynek gördülő ellenállása elhanyagolható, de erre csak a láda fér rá. Ezért a hordót az ábra szerint a targonca elé helyezzük, és a targoncával felgörgetjük a lejtőn, miközben a hordó a ládához súrlódik. A láda és a hordó között a súrlódási együttható µ = 0,4. A hordó tömege ugyanakkora, mint a láda és targonca együttes tömege.
   1. Mekkora erőt kell kifejtenünk a targoncára a "szerelvény" egyenletes felfelé haladása közben, ha hordó nélkül, csupán a ládával megterhelt targonca felfelé mozgatásához F₁ = 60 N nagyságú, lejtőirányú erő kell?
   2. Mennyi hő fejlődik a hordó és a láda érintkezési helyén az s = 100 m hosszú úton?

(Károlyházy Frigyes, Budapest)

4. a) Egy nyugalomban lévő jármű belso terében a karosszériához rögzített matematikai inga lóg függolegesen. Az ingatest tömege m. Az inga vékony fonala elszakad, ha azt 2mg-nél nagyobb erő terheli. A közegellenállás elhanyagolható, g = 10 m/s².
   1. Legfeljebb mekkora gyorsulással indulhat a jármű?
   2. A jármű lehetséges maximális gyorsulása esetén mekkora az ingatest talajhoz viszonyított gyorsulása akkor, amikor a fonál a legnagyobb szöget zárja be a függőleges iránnyal?

(Varga István, Békéscsaba)

4. b) Az ábra szerinti kapcsolásban az elhanyagolható belső ellenállású feszültségforrás három azonos ellenállású fogyasztót működtet. A feszültségmérők is azonosak. Az 1. számú feszültségmérő U₁ = 10 V feszültséget, 3. számú feszültségmérő U₃ = 8 V feszültséget jelez.

   

   1. Mekkorafeszültséget jelez a 2. számú feszültségmérő?
   2. Határozzuk meg a feszültségforrás feszültségét!

(Kotek László, Pécs)

1. a) Egy hőszigetelt tartályt hoszigetelo anyagból készült válaszfal oszt ketté. A tartály egyik, V₁ = 41,4 dm³ térfogatú részében, p₁ = 1,2 · 10⁵ Pa nyomású, T₁ = 300 K hőmérsékletű hélium van. A másik, V₂ = 51,75 dm³ térfogatú részét pedig p₂ = 2,4 · 10⁵ Pa nyomású, T₂ = 500 K hőmérsékletű hidrogén tölti ki.
   Mekkora lenne a gázkeverék hőmérséklete és a nyomása, ha a hőszigetelő anyagból készült válaszfalat kivennénk?

(Kiss Miklós, Gyöngyös)

1. b) Adott U₀ üresjárási feszültségű (elektromotoros erejű) és R_b belső ellenállású feszültségforrásokat egyszer sorba, másszor párhuzamosan kapcsoltunk. A keletkezett telepek kivezetéseire fogyasztót, és azzal sorosan egy elhanyagolható belső ellenállású áramerősség-mérő műszert kapcsoltunk. A fogyasztó ellenállása 50-szerese egy feszültségforrás belső ellenállásának (R_k = 50R_b ).
   1. Melyik kapcsolás esetén nagyobb a fogyasztó által felvett teljesítmény?
   2. Hány feszültségforrást kapcsoltunk össze, ha a soros kapcsolású telep esetén 10,75 amper, a párhuzamos kapcsolású telep esetén pedig 2,0 amper erősségű áramot jelzett a műszer?

(Kopcsa József, Debrecen)

2. A talaj felett h₁ = 1 m magasan elejtett gumilabda h₂ = 64 cm magasságig pattan vissza, g = 10 m/s².
   1. ) Sebességének hányadrészét veszíti el a labda a talajjal való ütközés során?
   2. ) Milyen kezdősebességgel kell a h₁ magasságból függőlegesen elindítani a labdát, hogy visszapattanjon az indítási pontba? Feltételezhető, hogy a labda sebességének sebességének nagysága minden ütközésben ugyanazon arányban csökken.

(Simon Péter, Pécs)

3. Két, d = 25 cm hosszúságú fonálingát felfüggesztünk egymástól 4d távolságban úgy, hogy az m = 0,2 kg tömegű ingatestek azonos magasságban legyenek. Az ingatesteket egy L₀ = 50 cm nyugalmi hosszúságú, elhanyagolható tömegu gumiszállal kötjük össze, majd függőleges helyzetükből egyszerre elengedjük őket. A gumiszál helyzete mindvégig vízszintesnek tekinthető. Az ingatestek távolsága a legnagyobb sebességű helyzetükben x = 70 cm. A közegellenállás elhanyagolható, g = 10 m/s².
   1. Mekkora erő hatására nyúlik meg a gumiszál 1 métert, ha megnyúlása egyenesen arányos a feszítőerővel?
   2. Határozzuk meg az ingatestek legnagyobb sebességét!

(Szkladányi András, Baja)

4. Vízszintes talajon nyugszik egy 2m = 2 kg tömegű kocsi, amelynek tetején egy R = 0,5 m sugarú, félgömb alakú tartály van rögzítve, alján egy pontszerunek tekintheto, m = 1 kg tömegű golyóval. A kocsi tengelyében v₀ = 3 m/s sebességgel érkezik egy ugyancsak 2m = 2 kg tömegű kocsi, amely az állóval abszolút rugalmasan és pillanatszerűen ütközik. Minden súrlódás elhanyagolható, g = 10 m/s².

   

   1. Az ütközés után milyen magasra csúszik fel a pontszerű golyó?
   2. Mekkora sebességgel mozognak a testek, miután a golyó visszaérkezett a tartály aljára?
   3. Mekkora erovel nyomja ekkor a golyó a tartályt?

(Holics László, Budapest)