Fizikai Szemle 2005/5. 191.o.
A KÁOSZ
Vannak közöttünk, akik gyakran hallják a kérdést: mi ez
a káosz a szobádban? A hétköznapi szóhasználatban a
káosz térbeli, statikus rendezetlenséget jelent. A modern
tudomány szóhasználatban viszont a káosz a mozgás egy
fajtája, mely az iskolában tanult mozgásokhoz képest
szokatlan tulajdonságokkal rendelkezik. Meglepő módon
ez a mozgásfajta mégis igen gyakori.
Az alábbi - az egyszerűség kedvéért a mechanika területéről
vett - példák segítenek megérteni a jelenséget.
Egyszerű példák
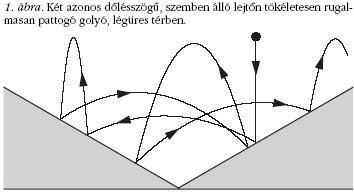
Kettős lejtőn pattogó golyó
A kaotikus mozgást mutató rendszerek közül talán a
legkézenfekvőbb a két szemben álló lejtő és a rajtuk
pattogó rugalmas labda által alkotott rendszer (1. ábra).
A mozgást tetszőleges hosszú ideig követve (a légellenállást
elhanyagoljuk) sem találunk semmilyen szabályosságot,
ismétlődést. A kaotikus viselkedés abból
adódik, hogy a másik lejtőre való átugrás után a labda
rendszerint nem pattan vissza oda, ahonnét jött. Így állandóan
új helyzetek állnak elő, az azonos oldalon történő,
egymás utáni ütközések száma pedig olyan típusú
véletlen számsorozatot ad, mintha dobókockákkal állítottuk
volna elő!
Golyó mozgása szabálytalan edényben
Amikor egy golyót szabálytalan alakú tálba helyezünk,
akkor mozgása meglehetősen szabálytalan lesz,
mielőtt az edény aljának valamely pontjában megnyugodna
(2. ábra ). A golyó megállása a súrlódás és a légellenállás
következménye. Ha állandó energiabetáplálást
biztosítunk, s a disszipálódott energiát pótoljuk
(pl. az edényt vízszintes síkban lassan mozgó felületre
helyezzük), akkor ismét (tetszőlegesen) hosszú ideig
tartó szabálytalan, kaotikus mozgást kapunk. A súrlódásmentes
esetben a mozgást az edény falának alakja
(mint potenciálgödör) határozza meg. Jól tudjuk, hogy
szabályos, forgásszimmetrikus edényben (mely centrális
potenciálnak felel meg) nem alakulhat ki szabálytalan
mozgás, hiszen az impulzusnyomaték megmaradása
miatt a pályák egyszer?ek. A szabálytalan esettel
kapcsolatos tapasztalatunk viszont azt mutatja: nem
gömb alakú napok körül a bolygópályák kaotikusak is
lehetnének!
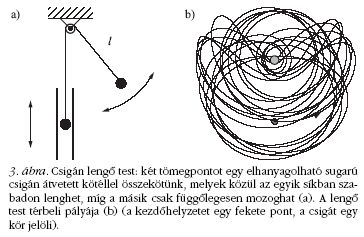
Lengő ejtőgép
Tekintsünk egy kicsiny csigán átvetett fonállal összekötött
két tömegpontot (3. ábra). A jól ismert középiskolai
feladatban mindkét pont csak függőlegesen mozoghat,
s egyenletesen gyorsuló mozgást végez (Atwood-féle
ejtőgép). Most azonban megengedjük az egyik tömegpont
függőleges síkban való kilengését is (az egyszerűség
kedvéért mindig feszes fonállal). A csak függőleges elmozdulást
lehetővé tevő hagyományos elrendezésben a
nehezebb tömeg mindig lehúzza a könnyebbet, viszont
az általánosított esetben sokkal érdekesebb a helyzet. Ha
ugyanis oldalirányban elegendően meglökjük a lengésre
képes testet, akkor - még ha a másik tömegpont nehezebb
is, és lefelé mozog - az egyre rövidülő lengő fonálon
a könnyebb test többször átfordul a csiga körül, egyre
jobban bepörög, s ezzel képessé válik arra, hogy a nehezebbet
visszahúzza. Így hosszú ideig tartó, bonyolult
kaotikus mozgás jöhet létre. A kilengésre képes test pályáját
a 3.b ábra mutatja.
Rezgő lemezen pattogó golyó
Tekintsünk egy időben szinuszosan fel-le mozgó vízszintes
lapon, például rezgő hangszórólemezen, függőlegesen
pattogó kisméretű golyót. A lemez rezgése periodikus,
a lemezzel való ütközés azonban már nem feltétlenül
az. A kaotikus viselkedést az okozza, hogy a golyó
repülési ideje általában nem azonos a lemez periódusidejével,
így az ütközések mindig különböző fázisokban
követik egymást.
A káosz jellemzői
A példáink eddig a kaotikus mozgás egyetlen tulajdonságát
hangsúlyozták: a szabálytalan időbeli viselkedést.
Mindegyik esetben megfigyelhető azonban, hogy ez a
vonás mindig együtt jár két további szokatlan tulajdonsággal
is. Az egyik az, hogy a két közeli pontból induló
mozgás rövid idő után erősen különbözővé válik: a kis
kezdeti különbségek drasztikus későbbi különbségre vezetnek!
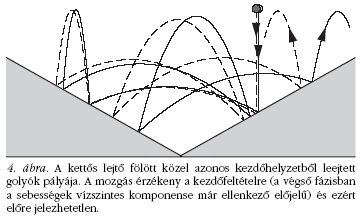
Ennek megfelelően a két, azonos magasságból
egymás mellett leejtett golyó kaotikus mozgása is gyorsan
szétválik (4. ábra). A kaotikus mozgás ezért hosszú távon
előre jelezhetetlen.
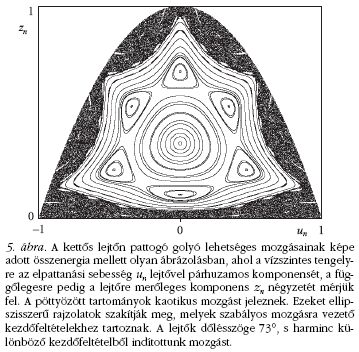
Amennyiben a lehetséges mozgások összességéről
áttekintő képet kívánunk kapni, érdemes bizonyos mintavételezést
alkalmazni. A golyók esetében például úgy,
hogy az n-edik ütközés pillanatában ábrázoljuk az elpattanási
sebesség két komponensét a sík egy pontjaként
(5. ábra). Így - a megfelelő ábrázolás segítségével - világossá
válik, hogy a káosz mégsem a teljes rendezetlenség,
hanem határozott struktúrával rendelkező bonyolult
mozgás. Ezt az újfajta struktúrát - melynek léte a másik
"szokatlan" tulajdonság - fraktál szerkezetnek nevezzük.
Káosz a hétköznapi életben
Mint példáink sejtetik, a káosz számos hétköznapi jelenséggel
kapcsolatos, melyeket itt csak röviden említünk.
Kaotikus folyamat például a flipperautomata golyójának
mozgása, a hulló falevél esése szélmentes időben, vagy a
rádió begerjedése is. A tésztagyúrás során a kezdetben
adott helyre koncentrálódott anyagok (tojás, só, cukor
stb.) rövid idő alatt az egész tésztában nagyjából egyenletesen
oszlanak el. E mögött az rejlik, hogy a sodrás és
nyújtás során minden egyes részecske kaotikus mozgást
végez. (Azaz, ha a szabályos, periodikus hajtogatások
során egyetlen részecskére szegeznénk a tekintetünket,
akkor annak mozgásában semmilyen szabályosságot sem
találnánk.) A festékek keveredése és a környezetszenynyezést
okozó részecskék szétterjedése is kaotikus folyamat.
A káosz szerepel számos műszaki jelenségben, például
a kerekek és szerszámgépelemek berezgésében, a
vontatott pótkocsik kilengésében. A pótkocsi-szerelvények
országúti vontatása ezért tilos számos országban.
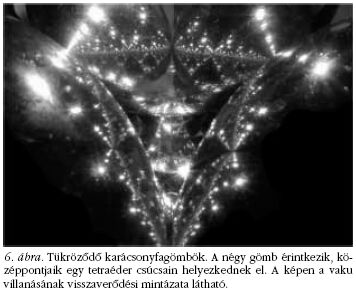
Négy érintkező karácsonyfadísz esetén nem golyók,
hanem fénysugarak verődnek vissza (többször is) sima
felületekről, mielőtt szemünkbe jutnak. A karácsonyfagömbök
egymáson való tükröződésének érdekes fraktálképei
(6. ábra ) tehát a fénysugarak kaotikus
"pattogásának"
hétköznapi életben is megfigyelhető következményei.
A káosz előfordul bizonyos kémiai reakciók időbeli
színváltozásaiban, biológiai jelenségekben (pl. egyes
járványok váratlan felbukkanásában), és jóval nagyobb
léptékben, például a Naprendszer alkotóelemeinek
mozgásában is. Kevéssé ismert, hogy amikor az augusztusi
éjszakákon hullócsillagok jelennek meg az égbolton,
kisméretű aszteroidák kaotikus mozgásának végső
fázisát látjuk.
Gruiz Márton, Tél Tamás
ELTE Elméleti Fizikai Tanszék