Fizikai Szemle 2005/7. 240.o.
GÁZLÉZEREK ÉS GÁZKISÜLÉSEK
Donkó Zoltán
MTA Szilárdtestfizikai és Optikai Kutatóintézet
A Központi Fizikai Kutató Intézetben (KFKI) az alapítás
óta folytak optikai és spektroszkópiai kutatások. A kutatások során
szerzett ismeretek és a kiépített infrastruktúra
teremtették meg annak alapját, hogy az Intézet az
országban elsőként tudott bekapcsolódni a gázlézerek
kutatásába, és ezen a területen később számos nemzetközileg
is elismert eredményt mutatott fel. A következőkben
áttekintjük a KFKI Fizikai Optikai Laboratóriumában,
majd az SZFKI Lézerfizikai Osztályán folyó, gázlézerekkel,
illetve gázkisülésekkel kapcsolatos kutatásokat,
hangsúlyt helyezve ezek történelmi vonatkozásaira
és fizikai alapjaira is.
A lézerek működése a fénysugárzás indukált emisszióval
történő erősítésén alapul (a LASER angol mozaikszó,
a Light Amplification by Stimulated Emission of Radiation
rövidítése). Az indukált emisszió során egy foton
egy gerjesztett állapotú atommal (vagy molekulával) kölcsönhatva
azt sugárzásra bírja. E folyamat lehetőségét
Einstein vetette fel 1917-ben. Ahhoz, hogy az indukált
emisszió az atomok spontán emissziója mellett lényegessé
válhassék, el kell érni, hogy valamely magasabban
fekvő energiájú állapotban több atom tartózkodjon, mint
az alacsonyabban fekvő állapotokban. Ezt a feltételt -
mivel termikus egyensúlytól eltérő állapotnak felel meg -
nehéz teljesíteni, ugyanis a különböző energiájú állapotok betöltésére
vonatkozó Boltzmann-eloszlás szerint
egyensúlyi rendszerben egy magasabban fekvő E2 energiájú
állapotban egy alacsonyabb E1 energiájú állapothoz
képest
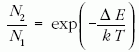
számú atom tartózkodik, ahol 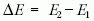 a két nívó
energiájának különbsége, k a Boltzmann-állandó és T a
hőmérséklet.
Gázkeverékekben létrehozott elektromos kisülések
fénykibocsátásának vizsgálata során már az 1930-as
években felfigyeltek egyes spektrumvonalak intenzitásának
anomális megerősödésére. A megfigyelt jelenséget
azzal lehetett magyarázni, hogy az egyik gáz gerjesztett
állapotú atomjai szelektíven populálják a másik
gáz atomjainak egyes energianívóit. Ez a szelektív gerjesztés
tehát lehetővé teszi a lézerműködéshez elengedhetetlenül
szükséges populációinverzió létrehozását.
Ezek a megfigyelések kevéssé jutottak be a tudományos
köztudatba, így még az 1950-es években megjelent Encyclopedia
of Physics egyik összefoglaló cikke is azt
állítja, hogy gázkisülésekben az indukált emisszió folyamata
elhanyagolható.
A sugárzás indukált emisszióval való erősítést először
a mikrohullámú tartományban oldották meg, ennek eredményeképpen
született meg 1954-ben a MASER (Microwave
Amplification by Stimulated Emission of Radiation
). Még hat évnek kellett eltelnie addig, amíg az optikai
tartományban is megvalósult egy hasonló elven (és a
MASER-rel ellentétben nyitott rezonátorban) működő
eszköz, az első rubinlézer. Egy évvel később épült meg
az első gázlézer (1961), amely hélium- és neongázok
keverékében működött, 1,15 µm infravörös hullámhosszon
[1]. A KFKI-ban ezt hamar követte az első magyarországi
gázlézer megépítése [2, 3], amely 1963. december
6-án kezdett el működni. A lézer fényképe az
1. ábrán látható.
Az első, vörös fényt sugárzó (632,8 nm hullámhosszon
működő) He-Ne lézer 1965-ben épült meg a KFKI-ban.
Később kidolgozták különböző teljesítményű (5-50 mW)
típusok gyártási technológiáját, illetve az éveksorán 40-
50 darabot gyártottak ezekből. Azokban az években,
amikor külföldről lényegében lehetetlen volt ilyen eszközöket
beszerezni, a KFKI-ban gyártott lézerek számos
hazai kutatóintézetben és egyetemen segítették a kutatómunkát,
emellett megkezdődött a lézerek orvosi felhasználása
is. E lézerek nagy részét még ma is használják.
a két nívó
energiájának különbsége, k a Boltzmann-állandó és T a
hőmérséklet.
Gázkeverékekben létrehozott elektromos kisülések
fénykibocsátásának vizsgálata során már az 1930-as
években felfigyeltek egyes spektrumvonalak intenzitásának
anomális megerősödésére. A megfigyelt jelenséget
azzal lehetett magyarázni, hogy az egyik gáz gerjesztett
állapotú atomjai szelektíven populálják a másik
gáz atomjainak egyes energianívóit. Ez a szelektív gerjesztés
tehát lehetővé teszi a lézerműködéshez elengedhetetlenül
szükséges populációinverzió létrehozását.
Ezek a megfigyelések kevéssé jutottak be a tudományos
köztudatba, így még az 1950-es években megjelent Encyclopedia
of Physics egyik összefoglaló cikke is azt
állítja, hogy gázkisülésekben az indukált emisszió folyamata
elhanyagolható.
A sugárzás indukált emisszióval való erősítést először
a mikrohullámú tartományban oldották meg, ennek eredményeképpen
született meg 1954-ben a MASER (Microwave
Amplification by Stimulated Emission of Radiation
). Még hat évnek kellett eltelnie addig, amíg az optikai
tartományban is megvalósult egy hasonló elven (és a
MASER-rel ellentétben nyitott rezonátorban) működő
eszköz, az első rubinlézer. Egy évvel később épült meg
az első gázlézer (1961), amely hélium- és neongázok
keverékében működött, 1,15 µm infravörös hullámhosszon
[1]. A KFKI-ban ezt hamar követte az első magyarországi
gázlézer megépítése [2, 3], amely 1963. december
6-án kezdett el működni. A lézer fényképe az
1. ábrán látható.
Az első, vörös fényt sugárzó (632,8 nm hullámhosszon
működő) He-Ne lézer 1965-ben épült meg a KFKI-ban.
Később kidolgozták különböző teljesítményű (5-50 mW)
típusok gyártási technológiáját, illetve az éveksorán 40-
50 darabot gyártottak ezekből. Azokban az években,
amikor külföldről lényegében lehetetlen volt ilyen eszközöket
beszerezni, a KFKI-ban gyártott lézerek számos
hazai kutatóintézetben és egyetemen segítették a kutatómunkát,
emellett megkezdődött a lézerek orvosi felhasználása
is. E lézerek nagy részét még ma is használják.

1. ábra. Az elsô magyar hélium-neon gázlézer fényképe. A fényerôsítés
az optikai padon rögzített kvarcüveg-csôben a külsô elektródás
nagyfrekvenciás térrel keltett kisülési plazmában jött létre. A lézerm?ködéshez
szükséges visszacsatolást a csô két oldalán egymással pontosan
szembeállított nagy reflexiójú ezüsttükrök biztosították. Háttérben a
vákuum- és gáztöltô rendszer látható.
A lézerműködés közege: alacsony
hőmérsékletű gázkisülési plazmák
A He-Ne lézer (és a többi később tárgyalt gázlézer) gerjesztési
mechanizmusa alacsony nyomású gázokban
elektromos árammal keltett plazmában lejátszódó ütközési
folyamatokon alapul. Az alkalmazott kisülések az
úgynevezett ködfénykisülés tartományában működnek. A
lézercső megfelelő geometriai kialakításával elérhető,
hogy a gázkisülési plazma azon része, amelyben a sugárzás
erősíthető, az optikai tengely mentén helyezkedjen
el. Mielőtt a lézer gerjesztési mechanizmusával foglalkoznánk,
először röviden tekintsük át az alacsony nyomású
gázkisülések fő jellemzőit és működésüknek alapjait. A
2. ábrán vázolt gázkisülési csőben alacsony (néhány
mbar) nyomású gáz van. A kisülési cső elektródáira megfelelően
nagy (~300-1000 V) feszültséget kapcsolva önfenntartó
ködfénykisülést hozhatunk létre, amely jellegzetes
térbeli tagozódást mutat. A kisülésnek több világító
és sötét térrésze jöhet létre, amelyeknek a fizikai paraméterei
igen eltérőek[4, 5]. Lézerek céljára kézenfekvően a
világító térrészek jöhetnek szóba, ugyanis ezekben számíthatunk a
fénysugárzás erősítésére.
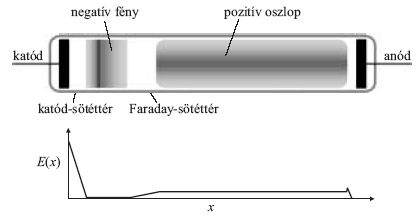
2. ábra. Az ábra felső részén az alacsony nyomású nemesgázban létrehozott
ködfénykisülés jellegzetes térbeli szerkezetét láthatjuk. Az ábra
alsó része az elektromos térerősség helyfüggését mutatja.
A katód közvetlen közelében megjelenik a katód-sötéttér,
amely nagy és közel lineárisan csökkenő elektromos
térrel jellemezhető. Itt a pozitív ionok jelentős tértöltést
hoznak létre. A katódból (nagyrészt a pozitív ionok becsapódásának
hatására) kilépő elektronok a nagy elektromos
térben felgyorsulnak, energiamérlegük pozitív,
azaz az elektromos tértől több energiát nyernek, mint
amennyit az ütközések során elveszítenek. A katódtól
távolodva következő térrészben, a negatív fényben az
elektromos térerősség igen kicsi. Itt az ionizációért és a
hatékony gerjesztésért a katód-sötéttérből belépő gyors
elektronok felelősek. Az anód felé tovább haladva kialakul
a Faraday-sötéttér, majd pedig a pozitív oszlop tartománya.
Ez utóbbi tetszőleges hosszúságú lehet, gyakorlatilag
semleges plazma alkotja, benne a kis (tengelyirányú)
elektromos térerősség olyan mértékű ionizációt
biztosít, amennyi a töltések radiális irányú veszteségeinek
fedezéséhez szükséges [4]. A számunkra érdekes
kisülésekben az áramot elektronok és (egyszeres) pozitív
töltésű ionok hordozzák . A lézerek gerjesztésében - mint
később látni fogjuk - különböző töltött és semleges részecskék
ütközései játszanak központi szerepet.
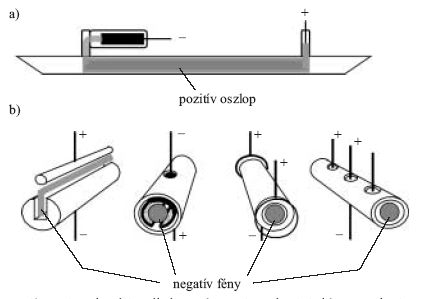
3. ábra. Lézerek céljára alkalmas a) pozitív oszlopú és b) üreges katódú
kisülési elrendezések (-: katód-, +: anódelektródák).
Pozitív oszlopú és üreges katódú lézerek
A He-Ne lézerben a kisülés pozitív oszlopú részét használjuk
fényerősítő közegként. A lézercső kialakítását a
3.a ábra, míg a lézer gerjesztési sémáját
a 4. ábra szemlélteti.
Az 1,15 µm-es hullámhosszúságú sugárzás esetében
a populációinverziót az elektronok és az alapállapotú
He-atomok ütközéseiben keletkező 23S metastabil He-atomok
és alapállapotú Ne-atomok energiakicserélő ütközései
hozzák létre, amelyek a Ne 2s állapotát szelektíven
populálják. Megjegyzendő, hogy ez utóbbi ütközéstípus
hatékonysága (hatáskeresztmetszete) erősen függ a
megfelelő szintek energiarezonanciájától, így ily módon
csak egyes meghatározott Ne-nívók gerjesztődhetnek. A
vörös He-Ne lézerben He 21S atomok populáljáka
lézerátmenet felső nívóját, a Ne 3s szintet.
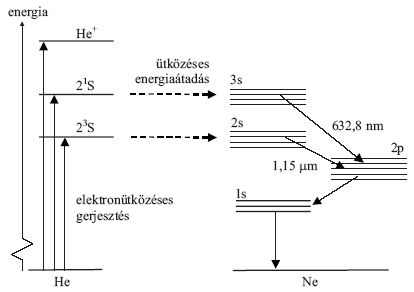
4. ábra. A He-Ne lézer gerjesztési mechanizmusa.
Az 1970-es években fontos szerepet kapott a fűtött
fémionlézerek kutatása. Ilyen típusú lézerre példaként a
kék (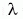 = 441,6 nm)
fényt sugárzó He-Cd+ lézer említhető,
amely ugyancsaka gázkisülés pozitív oszlop térrészében
működik. Lézerműködést a Cd+-ion több spektrumvonalán
hoztak létre [6], a szelektív gerjesztés mechanizmusa a
= 441,6 nm)
fényt sugárzó He-Cd+ lézer említhető,
amely ugyancsaka gázkisülés pozitív oszlop térrészében
működik. Lézerműködést a Cd+-ion több spektrumvonalán
hoztak létre [6], a szelektív gerjesztés mechanizmusa a
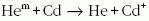
Penning-ionizációs folyamat (Hem metastabil állapotú
héliumatomokat jelöl). A szükséges Cd fémgőz-koncentrációt
egy, az anód környékén elhelyezkedő Cd-fémet
tartalmazó kályha biztosította. A kisülésbe jutva a Cd-atomok az
alacsony ionizációs potenciál miatt könnyen ionizálódtak,
és a pozitív oszlopú plazmában (azaz a lézer
aktív közegében) a katód felé haladva a kisülésben
egyenletes fémgőzsűrűség alakult ki.
A 70-es és 80-as évek központi témaköre az üreges
katódú lézerek kutatása volt (3.b és 5. ábra). A lézerek
ezen típusában a kisülés negatív fénye használható fel
aktív térrészként, üreges katódú kisülési elrendezésekben.
Az üreges katódokban egymással szembenálló katódfelületek
találhatók (pl. egy hengeres alakú katód
belsejében), és olyan járulékos folyamatok léphetnek fel,
amelyek jelentősen módosíthatják a kisülés tulajdonságait
[7]. A legfontosabb folyamat a gyors elektronok oszcilláló
mozgása a szemben elhelyezkedő katódfelületek között
kialakuló potenciálvölgyben [8, 9], ami az ionizáció
nagymértékű növekedéséhez vezethet, jelentősen növelve
a kisülés áramát. Míg a kisülések pozitív oszlopában a
gerjesztésben résztvevő elektronok energiaeloszlása közelítőleg
Maxwell-típusú (tipikusan néhány eV energiával),
addig a negatív fényben sokkal nagyobb energiájú
elektronok is jelen vannak, amelyek energiáját csak a katódesésnek
megfelelő feszültség (tipikusan 300-1000 V)
korlátozza. Ezek a nagyenergiájú elektronok jó lehetőséget
adnak magasan fekvő atomi és ion-energiaszintek
gerjesztésére.
Az üreges katódú lézerek három nagy csoportját a
következő típusok jelentik: i) nemesgáz-keverék lézerek,
ii) fűtött fémionlézerek, valamint iii) katódporlasztásos
fémionlézerek. Nemesgáz-keverék lézerekre példaként a
He-Ar+, He-Kr+, valamint a He-Ne-Xe+ típusok
említhetők [10-12]. A fűtött fémionlézerek közül az üreges katódú
He-Cd+ és He-Zn+ lézerek voltak jelentősek. Intézetünkben
mutatták ki, hogy a kisülés égési feszültségét, a
többi elektromos paramétertől függetlenül, a kisülés geometriájával
változtatni, optimalizálni lehet. Ezen elv alkalmazásával
számos új lézerátmenetet fedeztekfel. A 3.b ábra
néhány gyakran használt üreges katódú elektródakonstrukciót
mutat.

5. ábra. A gázlézer laboratórium az 1980-as években. A képen Jánossy
Mihály dolgozikaz üreges katódú He-Kr+ lézerrel.
A 70-es évektől kutatott lézerek közül külön ki kell
emelni a katódporlasztás révén működő fémionlézereket
- az első ilyen elven működő lézert a KFKI-ban fedezték
fel [13]. A lézer felfedezése lényegében véletlennek köszönhető:
rézből készült üreges katódú kisülésben He-
Ne lézert vizsgáltak, amikor a kilépő sugárzás teljesítményét
mérő műszer jelentős értéket jelzett anélkül, hogy
látható sugárzást figyelhettek volna meg. A sugárzás hullámhosszát
megmérve az 780,8 nm-es "váratlan" értéknek
adódott, amely egy Cu-II ionátmenet. Az átmenet felső
nívója energiarezonanciában áll a He+-ion alapállapotával,
így a lézer szelektíven gerjesztődhetett a
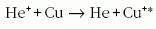
(közel) rezonáns töltéskicserélő folyamattal (lásd 6. ábra).
A gerjesztéshez szükséges rézatomokat a plazmából
a katódot bombázó nemesgázionok porlasztó hatása
juttatja a kisülésbe. Ily módon a szükséges fémgőzkoncentráció
nehezen elpárologtatható fémek esetében
is szobahőmérsékleten előállítható. Az eredmények
publikálását (1974) követően számos külföldi (NSZK,
USA-beli) kutatócsoport kezdett el foglalkozni katódporlasztásos
fémionlézerekkel. Ezek a laboratóriumok
hamarosan ultraibolya tartományba eső fémionátmeneteken
is létrehoztak lézereket, ezeken az átmeneteken
az SZFKI-ban csak évekkel később sikerült elérni lézerműködést.
Az Intézetünkben kidolgozott, szegmentált
üreges katódú kisülésben [14-16] azonban a lézer hatásfoka
jelenleg a legnagyobb, az irodalmi adatokkal összehasonlítva.
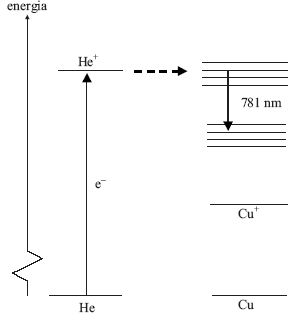
6. ábra. A He-Cu+ lézer gerjesztési mechanizmusa.
A szilárdtest- és félvezetőlézerek előretörése miatt a
gázlézerek kutatásának az utóbbi évtizedben a távoli
ultraibolya hullámhosszaknál volt jelentősége. Jelenleg a
224 nm-es hullámhosszon működő ezüstionlézert tanulmányozzuk.
Ez a lézer viszonylag olcsó fényforrás lehet a
Raman-spektroszkópia céljaira; a rövid hullámhossz nagy
hatásfokú gerjesztést és jó hatásfokú detektálást tesz lehetővé,
továbbá kiküszöbölhetővé teszi a zavaró fluoreszcenciajelet,
ami egyes szerves anyagok (pl. gyógyszerek)
vizsgálatánál alapvető fontosságú. A lézerrel 45 mW
impulzusüzemű teljesítményt értünk el [17].
Alacsonyhőmérsékletű plazmák kutatása
Mint láttuk, a gázlézerek működéséhez szükséges gerjesztési
folyamatok plazmaállapotú közegben játszódnak
le. Az itt használt ködfénykisülésekben létrejövő alacsony
ionizáltsági fokú plazmát gázlézerek gerjesztésére szolgáló
közeg mellett napjainkban széleskörűen alkalmazzák
számos más területen is, például a fényforrás-technológiában
(fénycsövekben és kisülési lámpákban), spektroszkópiai
fényforrásokban, valamint az integrált áramkörök
gyártásának technológiai lépéseiben, különböző
anyagok felületi tulajdonságainakmódosításánál
(szuperkemény, vagy biokompatibilis felületek létrehozása). Az
elmúlt évtized során az alacsony hőmérsékletű plazmák
kutatása az Osztályon önálló kutatási területté vált.
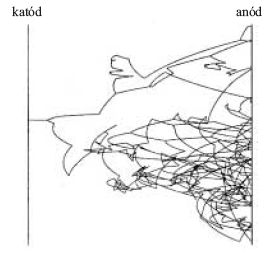
7. ábra. Egy szimulált elektronlavina képe. A trajektóriákon a "törések"
az egyes ütközéseknek felelnek meg, az "elágazások" az ionizációs folyamatokat
(új elektronok keletkezését) mutatják. (A szimuláció paraméterei:
U = 500 V, L = 1 cm, azaz E = 500 V/cm és p = 2,5 mbar He.)
A ködfénykisülések egyes térrészeinek leírására számos
próbálkozás történt analitikus módszerekkel. A XX.
század első fele és közepe időszakából legsikeresebbként
a pozitív oszlop Schottky-féle elmélete, illetve Little
és von Engel katódi térrészre kidolgozott elmélete említhető
(lásd pl. [4]). Az elmúlt 1-2 évtizedben a széles körben
hozzáférhetővé vált számítástechnikai lehetőségek
ezen a területen is számos nyitott kérdés megválaszolásához
adtak segítséget: lehetővé vált a töltött részecskék
mozgásának kinetikus elmélet szerinti leírása, elsősorban
direkt szimulációs módszerekkel. Numerikus módszerek
alkalmazásával számos olyan jelenség kvantitatív kezelése
vált lehetővé, amelyeket előzőleg csak kvalitatív
módon sikerült megérteni. Példaként említhető a gázkisülés-
fizika egyik legelemibb jelenségének, a gázkisülések begyújtásának a
vizsgálata, amely korrekt módon
csak numerikus módon írható le [18]. Az eredmények
lehetővé tették a korábbi "klasszikus" modellek pontosítását,
kiterjesztését, valamint a lézerek esetében a kísérleti
megfigyelések kvantitatív értelmezését.
A kinetikus elméletnek megfelelő transzportleírás alapjául
a Boltzmann-egyenlet, vagy a részecskeszimulációs
megközelítés szolgálhat. A Boltzmann-egyenlet általános
alakjában egy, a 6-dimenziós fázistérben felírt folytonossági
egyenlet, és megoldása általános esetben (3-dimenziós,
időfüggő probléma) igen nehéz (valós kisülésfizikai esetekben
általában még ma is megoldhatatlan) feladat. Stacionárius
megoldást keresve, illetve a térbeli dimenziószámot
csökkentve (pl. 1-dimenziós, vagy hengerszimmetrikus
rendszert feltételezve) az egyenlet egyszerűbb alakra
hozható. Megoldására azonban ezekben az esetekben is
bonyolult numerikus módszereket használnak, a problémák
analitikusan nem kezelhetőek. Az alternatívát jelentő
szimulációs módszerek, például a Monte Carlo szimuláció,
egyes részecskék követésén alapulnak, és a sokaságra jellemző
paramétereket az egyes részecskék jellemzőinek
átlagolásával adják meg. Ily módon a szimuláció alkalmazásával
valós képet kaphatunk a lejátszódó folyamatokról,
egyszerűen vizsgálható az események statisztikája.
Részecskeszimulációs módszerek segítségével számos
gázkisülési plazmát modelleztünk, például nemesgázkeverék-
kisülésekben [19], üreges katódú és nagyfeszültségű
kisülésekben [20], valamint lézerek céljára
szolgáló plazmaforrásokban [21]. Vizsgáltuk a gázban
történő ionizációk során kialakuló elektronlavinák jellemzőit,
megmutattuk, hogy az elektronlavinák fraktálszerkezettel
rendelkeznek [22]. A lavinák statisztikáját
vizsgálva arra a következtetésre jutottunk, hogy a gázok
átütése (szigetelő fázisból vezető fázisba történő átmenete)
a statisztikus fizikai értelmezés szerint kritikus
jelenségként írható le [23].
A Monte Carlo szimuláció során a részecskék
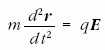
mozgásegyenletének integrálásával határozzuk meg a
részecskék trajektóriáit (m és q a részecske tömege, illetve
töltése, E az elektromos térerősség). A részecskék
mozgása során bekövetkező ütközések pozícióit az alábbi
egyenlet adja meg, amelyet a fenti mozgásegyenlettel
egyidejűleg integrálunk a pálya mentén:
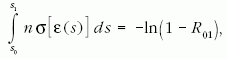
ahol s0 és s1 az előző és a következő ütközés pozíciója a
részecske pályája mentén, n a gáz sűrűsége, 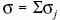 az
ütközési folyamatok hatáskeresztmetszeteinek összege,
az
ütközési folyamatok hatáskeresztmetszeteinek összege,
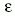 a részecske
kinetikus energiája és R01 a (0,1) intervallumon
egyenletes eloszlású véletlen számot jelöl [24].
A szabad úthossz befutása után a részecske különböző
ütközési folyamatokban vehet részt, az egyes folyamatok
bekövetkezésének valószínűsége arányos az ütközési
energiánál vett megfelelő hatáskeresztmetszet-értékekkel.
Ez a módszer azokban az esetekben használható, amikor
(az alacsony ionizációs foknak köszönhetően) elhanyagolható
a töltött részecskék közötti direkt kölcsönhatás
(pl. elektron-elektron ütközések), és így csak a töltött
részecskék (elektronok vagy ionok) transzportját kell
leírni a semleges háttérgázban. A szimuláció természetesen
lehetőséget ad arra, hogy az ionizációs folyamatokban
keletkező újabb elektronokat is kövessük, így megfigyelhetjük
a katódból induló elektronok által keltett
elektronlavinákat. A 7. ábra erre mutat egy példát - az
ábrán 2,5 mbar nyomású héliumgázban, L = 1 cm elektródatávolság
és U = 500 V feszültség esetén láthatjuk egy
elektronlavina Monte Carlo szimulációval kapott képét.
A szimulációkkal vizsgálható a kisülések időbeli felépülése,
illetve a töltött részecskék kinetikája bonyolultabb
elektródakonfigurációk esetében is. A 8. ábra egy
lézercélú szegmentált üreges katódú kisülés [15] keresztmetszetében
szemlélteti az ionizáció térbeli eloszlását. A
kisülés négy elektróda között jön létre, a két katód és a
két anód aktív felülete egy közös hengerpaláston helyezkedik
el. A görbült katódfelületek a kisülés tengelye irányába
fókuszálják a katódból kilépő, majd annak környezetében
felgyorsult elektronokat, ahol az ionizációs forrás
éles csúcsot mutat. Az erős fókuszálás a geometriai
viszonyok mellett a szegmentált üreges katódú kisülések
nagy égési feszültségével (400-1000 V) magyarázható. Az
ennek megfelelő energiákra felgyorsult elektronok szabad
úthossza igen nagy (összemérhető a katódüreg átmérőjével),
ugyanis az ütközési hatáskeresztmetszetek ebben
az energiatartományban már lényegesen kisebbek a
maximális értékeknél. A szimulációkkal megmutattuk,
hogy a szabályozott feszültségű üreges katódú kisülésben
a nagyobb feszültséget a töltéshordozók veszteségének
növekedése eredményezi, ilyenkor növekszik az
ionizáció a gyors elektronok hatására, továbbá közvetlen
bizonyítékát tudtuk adni a kisülésben az oszcilláló elektronok
jelenlétének [21].
Komplex kisülések önkonzisztens leírását teszik lehetővé
a részecskeszimulációs (Monte Carlo szimulációt)
és hidrodinamikai leírást egyesítő 1- és 2-dimenziós
önkonzisztens, úgynevezett hibrid modellek. (Önkonzisztens
leírás alatt itt azt értjük, hogy a töltött részecskék
olyan elektromos térben mozognak, amelyet a
saját töltéssűrűségük is befolyásol.) Hibrid modellek alkalmazásával
sikeresen vizsgáltuk gázkisülések különböző
jelenségeit: öngerjesztett oszcillációkat, az elektródakonfiguráció
hatását a kisülés jellemzőire, az üreges
katódú kisülések létrejöttét, a katódporlás jelenségét, a
kisülési plazmák fénykibocsátásának térbeli eloszlását
[25], a gázkisülések tranzienseit [26], illetve a He-Au+ lézer
gerjesztési viszonyait [27].
Egy további kutatási területként megemlítendő a folyadékfelületen
létrehozott atmoszférikus nyomású plazma
felhasználása környezetvédelmi analitikai célokra [28,
29]: az elektrolitkatódos atmoszférikus nyomású ködfénykisülés
(Electrolyte Cathode Atmospheric Glow Discharge,
ELCAD) a vizek nehézfémtartalmának közvetlen
meghatározására használható. Az utóbbi években részletesen
foglalkoztunk ezen speciális kisülés működési mechanizmusával.
Értelmeztük az összetétel hatását a katódporlásra,
vizsgáltuk a gáz- és elektronhőmérséklet-eloszlásokat,
valamint a kisülés gerjesztési viszonyait. E kutatások
gyakorlati alkalmazásaként szubnanogramm érzékenységű
többelemes fémdetektort építettünk kapilláris
elrendezésű ELCAD-ban.
a részecske
kinetikus energiája és R01 a (0,1) intervallumon
egyenletes eloszlású véletlen számot jelöl [24].
A szabad úthossz befutása után a részecske különböző
ütközési folyamatokban vehet részt, az egyes folyamatok
bekövetkezésének valószínűsége arányos az ütközési
energiánál vett megfelelő hatáskeresztmetszet-értékekkel.
Ez a módszer azokban az esetekben használható, amikor
(az alacsony ionizációs foknak köszönhetően) elhanyagolható
a töltött részecskék közötti direkt kölcsönhatás
(pl. elektron-elektron ütközések), és így csak a töltött
részecskék (elektronok vagy ionok) transzportját kell
leírni a semleges háttérgázban. A szimuláció természetesen
lehetőséget ad arra, hogy az ionizációs folyamatokban
keletkező újabb elektronokat is kövessük, így megfigyelhetjük
a katódból induló elektronok által keltett
elektronlavinákat. A 7. ábra erre mutat egy példát - az
ábrán 2,5 mbar nyomású héliumgázban, L = 1 cm elektródatávolság
és U = 500 V feszültség esetén láthatjuk egy
elektronlavina Monte Carlo szimulációval kapott képét.
A szimulációkkal vizsgálható a kisülések időbeli felépülése,
illetve a töltött részecskék kinetikája bonyolultabb
elektródakonfigurációk esetében is. A 8. ábra egy
lézercélú szegmentált üreges katódú kisülés [15] keresztmetszetében
szemlélteti az ionizáció térbeli eloszlását. A
kisülés négy elektróda között jön létre, a két katód és a
két anód aktív felülete egy közös hengerpaláston helyezkedik
el. A görbült katódfelületek a kisülés tengelye irányába
fókuszálják a katódból kilépő, majd annak környezetében
felgyorsult elektronokat, ahol az ionizációs forrás
éles csúcsot mutat. Az erős fókuszálás a geometriai
viszonyok mellett a szegmentált üreges katódú kisülések
nagy égési feszültségével (400-1000 V) magyarázható. Az
ennek megfelelő energiákra felgyorsult elektronok szabad
úthossza igen nagy (összemérhető a katódüreg átmérőjével),
ugyanis az ütközési hatáskeresztmetszetek ebben
az energiatartományban már lényegesen kisebbek a
maximális értékeknél. A szimulációkkal megmutattuk,
hogy a szabályozott feszültségű üreges katódú kisülésben
a nagyobb feszültséget a töltéshordozók veszteségének
növekedése eredményezi, ilyenkor növekszik az
ionizáció a gyors elektronok hatására, továbbá közvetlen
bizonyítékát tudtuk adni a kisülésben az oszcilláló elektronok
jelenlétének [21].
Komplex kisülések önkonzisztens leírását teszik lehetővé
a részecskeszimulációs (Monte Carlo szimulációt)
és hidrodinamikai leírást egyesítő 1- és 2-dimenziós
önkonzisztens, úgynevezett hibrid modellek. (Önkonzisztens
leírás alatt itt azt értjük, hogy a töltött részecskék
olyan elektromos térben mozognak, amelyet a
saját töltéssűrűségük is befolyásol.) Hibrid modellek alkalmazásával
sikeresen vizsgáltuk gázkisülések különböző
jelenségeit: öngerjesztett oszcillációkat, az elektródakonfiguráció
hatását a kisülés jellemzőire, az üreges
katódú kisülések létrejöttét, a katódporlás jelenségét, a
kisülési plazmák fénykibocsátásának térbeli eloszlását
[25], a gázkisülések tranzienseit [26], illetve a He-Au+ lézer
gerjesztési viszonyait [27].
Egy további kutatási területként megemlítendő a folyadékfelületen
létrehozott atmoszférikus nyomású plazma
felhasználása környezetvédelmi analitikai célokra [28,
29]: az elektrolitkatódos atmoszférikus nyomású ködfénykisülés
(Electrolyte Cathode Atmospheric Glow Discharge,
ELCAD) a vizek nehézfémtartalmának közvetlen
meghatározására használható. Az utóbbi években részletesen
foglalkoztunk ezen speciális kisülés működési mechanizmusával.
Értelmeztük az összetétel hatását a katódporlásra,
vizsgáltuk a gáz- és elektronhőmérséklet-eloszlásokat,
valamint a kisülés gerjesztési viszonyait. E kutatások
gyakorlati alkalmazásaként szubnanogramm érzékenységű
többelemes fémdetektort építettünk kapilláris
elrendezésű ELCAD-ban.
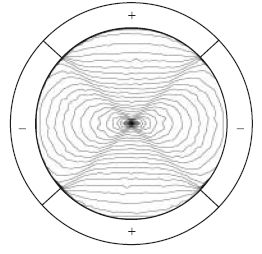
8. ábra. Az ionizáció tipikus térbeli eloszlása (forrásfüggvénye) ultraibolya
lézerek céljára használt üreges katódú kisülés keresztmetszetében
[21]. (A kisülés paraméterei: U = 625 V, p = 15 mbar He. A kisülés
közepén a sűrűsödő szintvonalak az igen intenzív ionizációt jelzik, -:
katód-, +: anódelektródák.)
Erősen csatolt plazmákk utatása
Az eddig tárgyalt plazmatípusokban a részecskék kölcsönhatásából
származó potenciális energia elhanyagolható
az Ekin ~ kT kinetikus energiához képest, a két energiatag
arányát megadó csatolási paraméter, 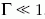 . Egyes
nemklasszikus plazmákban viszont a kölcsönhatási (potenciális)
energia (lényegesen) nagyobb lehet a kinetikus
energiánál, és ekkor erősen csatolt plazmákról beszélünk,
amelyekre
. Egyes
nemklasszikus plazmákban viszont a kölcsönhatási (potenciális)
energia (lényegesen) nagyobb lehet a kinetikus
energiánál, és ekkor erősen csatolt plazmákról beszélünk,
amelyekre 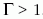 . Erősen csatolt plazmákra példa a
neutroncsillagok köpenyében, fehér törpecsillagokban,
óriásbolygók belsejében található anyagállapot, ahol a
teljesen ionizált atomok iontörzsei erősen csatolt rendszert
alkotnak, miközben a degenerált állapotú elektronok
egy semlegesítő hátteret képeznek. Mesterségesen
létrehozott erősen csatolt plazmákra példaként említhetők
a csapdákban tárolt ionok, amelyek esetében a hőmérséklet
igen alacsony lehet, és így a rendszerek kristályos
állapotba kerülhetnek [30].
A plazmák speciális (és egyre inkább az érdeklődés
középpontjába kerülő) fajtáját képviselik a komplex plazmák,
amelyekben az elektronok, ionok és semleges gázatomok
(molekulák) mellett nanométer-mikrométer méretű
részecskék is jelen vannak. Ilyen rendszerekre asztrofizikai
példaként a csillagközi por, az üstökösök csóvája,
a Szaturnusz és az Uránusz gyűrűi említhetők. A porrészecskék
az ultraibolya sugárzás miatti elektronemisszió,
vagy nagyenergiájú részecskékkel való ütközések
hatására elektromosan töltötté válnak, így a plazma többi
összetevőjével kölcsönhatásba kerülnek, és azokhoz hasonlóan
reagálnak a külső elektromos és mágneses térre.
Mivel a plazma egyéb összetevőihez képest az igen nagy
méretű porrészecskék nagy töltést vehetnek fel, a porrészecskék
gyakran erősen csatolt rendszert alkotnak, plazmakristályok
keletkezhetnek, amint azt laboratóriumi kísérletekben
is megmutatták.
Az erősen csatolt plazmák területén végzett munkánk
Coulomb- és Yukawa-kölcsönhatási potenciállal jellemezhető
sokrészecske-rendszerekben lejátszódó jelenségek
nyomon követésére, különleges körülmények között
található anyagoktulajdonságainakleírására irányul. A
statikus termodinamikai jellemzők mellett a szimulációkkal
vizsgáltuk az erősen csatolt rendszereket alkotó részecskék
lokalizációját [31], valamint a rendszerek kollektív
(dinamikus) jelenségeit [32, 33]. Nemegyensúlyi molekuladinamikai
szimulációs módszerekkel meghatároztuk
a rendszerek egyes transzportjellemzőit (nyíró viszkozitást
és hővezetési együtthatót) [34, 35].
. Erősen csatolt plazmákra példa a
neutroncsillagok köpenyében, fehér törpecsillagokban,
óriásbolygók belsejében található anyagállapot, ahol a
teljesen ionizált atomok iontörzsei erősen csatolt rendszert
alkotnak, miközben a degenerált állapotú elektronok
egy semlegesítő hátteret képeznek. Mesterségesen
létrehozott erősen csatolt plazmákra példaként említhetők
a csapdákban tárolt ionok, amelyek esetében a hőmérséklet
igen alacsony lehet, és így a rendszerek kristályos
állapotba kerülhetnek [30].
A plazmák speciális (és egyre inkább az érdeklődés
középpontjába kerülő) fajtáját képviselik a komplex plazmák,
amelyekben az elektronok, ionok és semleges gázatomok
(molekulák) mellett nanométer-mikrométer méretű
részecskék is jelen vannak. Ilyen rendszerekre asztrofizikai
példaként a csillagközi por, az üstökösök csóvája,
a Szaturnusz és az Uránusz gyűrűi említhetők. A porrészecskék
az ultraibolya sugárzás miatti elektronemisszió,
vagy nagyenergiájú részecskékkel való ütközések
hatására elektromosan töltötté válnak, így a plazma többi
összetevőjével kölcsönhatásba kerülnek, és azokhoz hasonlóan
reagálnak a külső elektromos és mágneses térre.
Mivel a plazma egyéb összetevőihez képest az igen nagy
méretű porrészecskék nagy töltést vehetnek fel, a porrészecskék
gyakran erősen csatolt rendszert alkotnak, plazmakristályok
keletkezhetnek, amint azt laboratóriumi kísérletekben
is megmutatták.
Az erősen csatolt plazmák területén végzett munkánk
Coulomb- és Yukawa-kölcsönhatási potenciállal jellemezhető
sokrészecske-rendszerekben lejátszódó jelenségek
nyomon követésére, különleges körülmények között
található anyagoktulajdonságainakleírására irányul. A
statikus termodinamikai jellemzők mellett a szimulációkkal
vizsgáltuk az erősen csatolt rendszereket alkotó részecskék
lokalizációját [31], valamint a rendszerek kollektív
(dinamikus) jelenségeit [32, 33]. Nemegyensúlyi molekuladinamikai
szimulációs módszerekkel meghatároztuk
a rendszerek egyes transzportjellemzőit (nyíró viszkozitást
és hővezetési együtthatót) [34, 35].
Összefoglalás, jelenlegi kutatási irányok
A gázlézerekterületén jelenleg a He-Ag+ (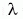 = 224 nm)
lézer kutatása és praktikus lézer fejlesztése a legfontosabb
feladat, elsősorban Raman-spektroszkópiai vizsgálatokhoz.
Az elektrolitkatódos atmoszférikus nyomású kisülés
esetén az egyre nagyobb érzékenység (kisebb kimutatható
szennyezőkoncentráció) elérésén dolgozunk.
Az alacsony nyomású gázkisülések (kis ionizáltsági
fokú plazmáinak) területén legfontosabb az önkonzisztens,
első elvekből kiinduló modellezési eljárások fejlesztése.
Elsődlegesen a PIC (Particle-In-Cell) szimulációs
módszerek [36] továbbfejlesztésére koncentrálunk. A
PIC-módszer a töltött részecskék mozgását a klasszikus
mozgásegyenlettel írja le, a részecskékre ható erő az
elektromos térerősségből adódik, ezt pedig a töltött
részecskék jelenléte és az elektródákra kapcsolt potenciál
határozza meg. A mozgásegyenlet és a Poisson-egyenlet
együttes megoldása biztosítja az eredmények
önkonzisztens voltát. Egy évtizeddel ezelőtt csak az
akkori szuperszámítógépek adtak lehetőséget ilyen modelleken
alapuló számításokra, a módszer szélesebb
körű elterjedése a számítástechnikai háttér igen gyors
fejlődésének köszönhető.
Az erősen csatolt plazmák vizsgálata egy új, dinamikusan
fejlődő terület. Itt elsősorban a Coulomb- és Yukawa-kölcsönhatási
potenciállal jellemezhető sokrészecskerendszereket
kutatjuk. Az eredményeknek a laboratóriumban
létrehozott állapotokvizsgálata mellett asztrofizikai
jelentőségük is van.
A jövőben tervezett kutatási témáink elsősorban alapkutatás-
motiváltak, de az itt szerezhető ismeretek az alkalmazások szempontjából
is hasznosak lehetnek .
= 224 nm)
lézer kutatása és praktikus lézer fejlesztése a legfontosabb
feladat, elsősorban Raman-spektroszkópiai vizsgálatokhoz.
Az elektrolitkatódos atmoszférikus nyomású kisülés
esetén az egyre nagyobb érzékenység (kisebb kimutatható
szennyezőkoncentráció) elérésén dolgozunk.
Az alacsony nyomású gázkisülések (kis ionizáltsági
fokú plazmáinak) területén legfontosabb az önkonzisztens,
első elvekből kiinduló modellezési eljárások fejlesztése.
Elsődlegesen a PIC (Particle-In-Cell) szimulációs
módszerek [36] továbbfejlesztésére koncentrálunk. A
PIC-módszer a töltött részecskék mozgását a klasszikus
mozgásegyenlettel írja le, a részecskékre ható erő az
elektromos térerősségből adódik, ezt pedig a töltött
részecskék jelenléte és az elektródákra kapcsolt potenciál
határozza meg. A mozgásegyenlet és a Poisson-egyenlet
együttes megoldása biztosítja az eredmények
önkonzisztens voltát. Egy évtizeddel ezelőtt csak az
akkori szuperszámítógépek adtak lehetőséget ilyen modelleken
alapuló számításokra, a módszer szélesebb
körű elterjedése a számítástechnikai háttér igen gyors
fejlődésének köszönhető.
Az erősen csatolt plazmák vizsgálata egy új, dinamikusan
fejlődő terület. Itt elsősorban a Coulomb- és Yukawa-kölcsönhatási
potenciállal jellemezhető sokrészecskerendszereket
kutatjuk. Az eredményeknek a laboratóriumban
létrehozott állapotokvizsgálata mellett asztrofizikai
jelentőségük is van.
A jövőben tervezett kutatási témáink elsősorban alapkutatás-
motiváltak, de az itt szerezhető ismeretek az alkalmazások szempontjából
is hasznosak lehetnek .
»«
Az itt bemutatott, több évtizedet átfogó kutatásoknak a
Kroó Norbert, majd Kollár János által vezetett MTA
SZFKI adott, illetve ad otthont. A korábbi, illetve jelenlegi
kutatásokat támogató szervezetek (OMFB, OTKA,
NATO, MTA, NSF) mellett őket illeti köszönet a kutatómunka
segítéséért és feltételeinek biztosításáért. Végezetül
álljon itt azon kollégák neve, akik részt vettek az
ismertetett munkában: Apai Pál, Ádám Ferenc, Bakos
József, Bánó Gergely, Bergou János, Császár György,
Csillag László, Csonka Lajos, Ferencz Kárpát, Hartmann
Péter, Horváth Péter, Jánossy Mihály, Kántor Károly,
Kaspari Jánosné, Kutasi Kinga, Lutter András,
Majorosi Antal, Mezei Pál, M. Császár Lili, Rózsa Károly,
Rubin György, Salamon Tamás, Sárközi Elek, Szalai
László, Szántó Sándor, Szigeti János, Thomanné
Forgács Judit, Tóth József, Varga Péter.
Irodalom
1. A. JAVAN, W.R. BENNETT, JR., D.R. HERRIOTT: Population inversion
and continuous optical maser oscillation in a gas discharge containing
a He-Ne mixture - Phys. Rev. Lett. 6 (1961) 106
2. Magyar laser a Központi Fizikai Kutató Intézetben - Magyar Nemzet
1963. dec. 15.
3. J. BAKOS, L. CSILLAG, K. KÁNTOR, P. VARGA: Ezüsttükrös nagyfrekvenciás
gerjesztésű He-Ne laser - KFKI Közlemények 13 (1965) 195
4. G. FRANCIS: The glow discharge at low pressure in Encyclopedia of
Physics, XXII (1956) 53, Springer, Berlin
5. A. VON ENGEL: Ionized Gases - Clarendon Press, Oxford, 1965.
6. L. CSILLAG, M. JÁNOSSY, K. KÁNTOR, K. RÓZSA, T. SALAMON: Investigations
on a continuous wave 4416 Cd ion laser - J. Phys. D: Appl.
Phys. 3 (1970) 64
7. P.F. LITTLE, A. VON ENGEL: The hollow-cathode effect and the theory
of glow discharges - Proc. Roy. Soc. (London) A224 (1954) 209
8. H. HELM: Experimenteller Nachweis des Pendel-Effektes in einer
zylindrischen Niederdruck-Hohlkathoden-Entladung in Argon - Z.
Naturforschung 27a (1972) 1812
9. Z. DONKÓ: A study of the motion of high-energy electrons in a
helium hollow cathode discharge - Z. Naturforschung 48a (1993)
10. M. JÁNOSSY, L. CSILLAG, K. RÓZSA: CW laser oscillation in a He-Ar
hollow cathode discharge - Phys. Lett. 63A (1977) 231
11. M. JÁNOSSY, K. RÓZSA, P. APAI, L. CSILLAG: He-Kr ion laser in a D. C.
hollow cathode discharge - Optics Commun. 49 (1984) 278
12. M. JÁNOSSY, P. MEZEI, P. HORVÁTH: On the excitation of Xe-II lines in
a He-Ne-Xe hollow cathode laser - Optics Commun. 65 (1988) 287
13. L. CSILLAG, M. JÁNOSSY K. RÓZSA, T. SALAMON: Near infrared cw laser
oscillation in Cu-II - Phys. Lett. 50A (1974) 13
14. K.A. PEARD, R.C. TOBIN, K. RÓZSA, Z. DONKÓ: A high-voltage hollowcathode
Au-II 282 nm laser - IEEE J. Quantum Electronics 30
(1994) 1181
15. R.C. TOBIN, K.A. PEARD, G. BODE, K. RÓZSA, Z. DONKÓ, L. SZALAI:
High-gain hollow-cathode metal ion lasers for the UV and VUV -
IEEE Journal of Selected Topics in Quantum Electronics 1 (1995)
830
16. Z. DONKÓ, L. SZALAI, K. RÓZSA, M. ULBEL, M. PÖCKL: High gain ultraviolet
Cu-II laser in a segmented hollow cathode discharge - IEEE J.
Quantum Electronics 34 (1998) 47
17. G. BÁNÓ, P. HORVÁTH, L. CSILLAG, J. GLOSÍK, T.M. ADAMOWICZ, K.
RÓZSA: 224 nm segmented hollow cathode silver ion laser - Appl.
Phys. B 80 (2005) 215
18. P. HARTMANN, Z. DONKÓ, G. BÁNÓ, L. SZALAI, K. RÓZSA: Effect of different
elementary processes on the breakdown in low-pressure helium
gas - Plasma Sources Sci. Technol. 9 (2000) 183
19. Z. DONKÓ, M. JÁNOSSY: Model of the cathode dark space in noble
gas mixture discharges - J. Phys. D: Appl. Phys. 25 (1992) 1323
20. Z. DONKÓ, K. RÓZSA, R.C. TOBIN, K.A. PEARD: Modeling and measurements
on an obstructed glow discharge in helium - Phys. Rev.
E 49 (1994) 3283
21. Z. DONKÓ, K. RÓZSA, R.C. TOBIN: Monte Carlo analysis of the
electrons' motion in a segmented hollow cathode discharge - J. Phsy. D:
Appl. Phys. 29 (1996) 105-114
22. Z. DONKÓ, I. PÓCSIK: On the fractal structure of electron avalanches
- Fractals 1 (1993) 939
23. Z. DONKÓ: Avalanches and bursts in low pressure helium gas below
the breakdown voltage - Phys. Rev. E 51 (1995) 3934
24. J.P. BOEUF, E. MARODE: A Monte Carlo analysis of an electron
swarm in a non-uniform field: the cathode region of a glow discharge
in helium - J. Phys. D: Appl. Phys. 15 (1982) 2169
25. D. MARIC, K. KUTASI, G. MALOVIC, Z. DONKÓ, Z.LJ. PETROVIC: Axial
emission profiles and apparent secondary electron yield in abnormal
glow discharges in argon - Eur. Phys. J. D 21 (2002) 73
26. Z. DONKÓ: Heavy-particle hybrid modeling of transients in a direct-
current argon discharge - J. Appl. Phys. 88 (2000) 2226
27. G. BÁNÓ, L. SZALAI, P. HORVÁTH, K. KUTASI, Z. DONKÓ, K. RÓZSA,
T.M. ADAMOWICZ: Au-II 282 nm segmented hollow cathode laser:
parametric studies and modeling - J. Appl. Phys. 92 (2002) 6372
28. P. MEZEI, T. CSERFALVI, H.J. KIM, M.A. MOTTALEB: The influence of
chlorine on the intensity of metal atomic lines emitted by an electrolyte
cathode atmospheric glow discharge - The Analyst 126
(2001) 712
29. T. CSERFALVI, P. MEZEI: Subnanogram sensitive multimetal detector
with atmospheric electrolyte cathode glow discharge - Journ. Anal.
At. Spectr. 18 (2003) 596
30. H. THOMAS, G.E. MORFILL, V.G. DEMMEL: Plasma crystal: Coulomb
crystallization in a dusty plasma - Phys. Rev. Lett. 73 (1994) 652
31. Z. DONKÓ, G.J. KALMAN, K.I. GOLDEN: Caging of particles in one-component
plasmas - Phys. Rev. Lett. 88 (2002) 225001
32. Z. DONKÓ, G.J. KALMAN, P. HARTMANN, K.I. GOLDEN, K. KUTASI: Dynamical
structure functions, collective modes and energy gap in
charged particle bilayers - Phys. Rev. Lett. 90 (2003) 226804
33. G.J. KALMAN, P. HARTMANN, Z. DONKÓ, M. ROSENBERG: Two-dimensional
Yukawa liquids: Correlation and dynamics - Phys. Rev.
Lett. 92 (2004) 065001
34. Z. DONKÓ, B. NYÍRI, L. SZALAI, S.HOLLÓ: Thermal conductivity of the
classical electron one-component plasma - Phys. Rev. Lett. 81
(1998) 1622
35. Z. DONKÓ, B. NYÍRI: Molecular dynamics calculation of the thermal
conductivity and shear viscosity of the classical one-component
plasma - Physics of Plasmas 7 (2000) 45
36. C.K. BIRDSALL: Particle-in-cell charged-particle simulations plus
Monte Carlo collisions with neutral atoms, PIC-MCC - IEEE Trans.
Plasma Sci. PS-19 (1991) 65
___________________________________________
A Magyar Tudományos Akadémián 2004. szeptember 29-én Kroó Norbert
akadémikus tiszteletére rendezett tudományos ülésen elhangzott
elôadás szerkesztett változata.
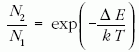
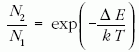
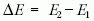 a két nívó
energiájának különbsége, k a Boltzmann-állandó és T a
hőmérséklet.
Gázkeverékekben létrehozott elektromos kisülések
fénykibocsátásának vizsgálata során már az 1930-as
években felfigyeltek egyes spektrumvonalak intenzitásának
anomális megerősödésére. A megfigyelt jelenséget
azzal lehetett magyarázni, hogy az egyik gáz gerjesztett
állapotú atomjai szelektíven populálják a másik
gáz atomjainak egyes energianívóit. Ez a szelektív gerjesztés
tehát lehetővé teszi a lézerműködéshez elengedhetetlenül
szükséges populációinverzió létrehozását.
Ezek a megfigyelések kevéssé jutottak be a tudományos
köztudatba, így még az 1950-es években megjelent Encyclopedia
of Physics egyik összefoglaló cikke is azt
állítja, hogy gázkisülésekben az indukált emisszió folyamata
elhanyagolható.
A sugárzás indukált emisszióval való erősítést először
a mikrohullámú tartományban oldották meg, ennek eredményeképpen
született meg 1954-ben a MASER (Microwave
Amplification by Stimulated Emission of Radiation
). Még hat évnek kellett eltelnie addig, amíg az optikai
tartományban is megvalósult egy hasonló elven (és a
MASER-rel ellentétben nyitott rezonátorban) működő
eszköz, az első rubinlézer. Egy évvel később épült meg
az első gázlézer (1961), amely hélium- és neongázok
keverékében működött, 1,15 µm infravörös hullámhosszon
[1]. A KFKI-ban ezt hamar követte az első magyarországi
gázlézer megépítése [2, 3], amely 1963. december
6-án kezdett el működni. A lézer fényképe az
1. ábrán látható.
Az első, vörös fényt sugárzó (632,8 nm hullámhosszon
működő) He-Ne lézer 1965-ben épült meg a KFKI-ban.
Később kidolgozták különböző teljesítményű (5-50 mW)
típusok gyártási technológiáját, illetve az éveksorán 40-
50 darabot gyártottak ezekből. Azokban az években,
amikor külföldről lényegében lehetetlen volt ilyen eszközöket
beszerezni, a KFKI-ban gyártott lézerek számos
hazai kutatóintézetben és egyetemen segítették a kutatómunkát,
emellett megkezdődött a lézerek orvosi felhasználása
is. E lézerek nagy részét még ma is használják.
a két nívó
energiájának különbsége, k a Boltzmann-állandó és T a
hőmérséklet.
Gázkeverékekben létrehozott elektromos kisülések
fénykibocsátásának vizsgálata során már az 1930-as
években felfigyeltek egyes spektrumvonalak intenzitásának
anomális megerősödésére. A megfigyelt jelenséget
azzal lehetett magyarázni, hogy az egyik gáz gerjesztett
állapotú atomjai szelektíven populálják a másik
gáz atomjainak egyes energianívóit. Ez a szelektív gerjesztés
tehát lehetővé teszi a lézerműködéshez elengedhetetlenül
szükséges populációinverzió létrehozását.
Ezek a megfigyelések kevéssé jutottak be a tudományos
köztudatba, így még az 1950-es években megjelent Encyclopedia
of Physics egyik összefoglaló cikke is azt
állítja, hogy gázkisülésekben az indukált emisszió folyamata
elhanyagolható.
A sugárzás indukált emisszióval való erősítést először
a mikrohullámú tartományban oldották meg, ennek eredményeképpen
született meg 1954-ben a MASER (Microwave
Amplification by Stimulated Emission of Radiation
). Még hat évnek kellett eltelnie addig, amíg az optikai
tartományban is megvalósult egy hasonló elven (és a
MASER-rel ellentétben nyitott rezonátorban) működő
eszköz, az első rubinlézer. Egy évvel később épült meg
az első gázlézer (1961), amely hélium- és neongázok
keverékében működött, 1,15 µm infravörös hullámhosszon
[1]. A KFKI-ban ezt hamar követte az első magyarországi
gázlézer megépítése [2, 3], amely 1963. december
6-án kezdett el működni. A lézer fényképe az
1. ábrán látható.
Az első, vörös fényt sugárzó (632,8 nm hullámhosszon
működő) He-Ne lézer 1965-ben épült meg a KFKI-ban.
Később kidolgozták különböző teljesítményű (5-50 mW)
típusok gyártási technológiáját, illetve az éveksorán 40-
50 darabot gyártottak ezekből. Azokban az években,
amikor külföldről lényegében lehetetlen volt ilyen eszközöket
beszerezni, a KFKI-ban gyártott lézerek számos
hazai kutatóintézetben és egyetemen segítették a kutatómunkát,
emellett megkezdődött a lézerek orvosi felhasználása
is. E lézerek nagy részét még ma is használják.




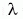 = 441,6 nm)
fényt sugárzó He-Cd+ lézer említhető,
amely ugyancsaka gázkisülés pozitív oszlop térrészében
működik. Lézerműködést a Cd+-ion több spektrumvonalán
hoztak létre [6], a szelektív gerjesztés mechanizmusa a
= 441,6 nm)
fényt sugárzó He-Cd+ lézer említhető,
amely ugyancsaka gázkisülés pozitív oszlop térrészében
működik. Lézerműködést a Cd+-ion több spektrumvonalán
hoztak létre [6], a szelektív gerjesztés mechanizmusa a
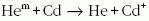

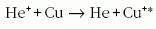


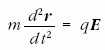
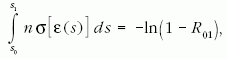
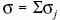 az
ütközési folyamatok hatáskeresztmetszeteinek összege,
az
ütközési folyamatok hatáskeresztmetszeteinek összege,
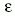 a részecske
kinetikus energiája és R01 a (0,1) intervallumon
egyenletes eloszlású véletlen számot jelöl [24].
A szabad úthossz befutása után a részecske különböző
ütközési folyamatokban vehet részt, az egyes folyamatok
bekövetkezésének valószínűsége arányos az ütközési
energiánál vett megfelelő hatáskeresztmetszet-értékekkel.
Ez a módszer azokban az esetekben használható, amikor
(az alacsony ionizációs foknak köszönhetően) elhanyagolható
a töltött részecskék közötti direkt kölcsönhatás
(pl. elektron-elektron ütközések), és így csak a töltött
részecskék (elektronok vagy ionok) transzportját kell
leírni a semleges háttérgázban. A szimuláció természetesen
lehetőséget ad arra, hogy az ionizációs folyamatokban
keletkező újabb elektronokat is kövessük, így megfigyelhetjük
a katódból induló elektronok által keltett
elektronlavinákat. A 7. ábra erre mutat egy példát - az
ábrán 2,5 mbar nyomású héliumgázban, L = 1 cm elektródatávolság
és U = 500 V feszültség esetén láthatjuk egy
elektronlavina Monte Carlo szimulációval kapott képét.
A szimulációkkal vizsgálható a kisülések időbeli felépülése,
illetve a töltött részecskék kinetikája bonyolultabb
elektródakonfigurációk esetében is. A 8. ábra egy
lézercélú szegmentált üreges katódú kisülés [15] keresztmetszetében
szemlélteti az ionizáció térbeli eloszlását. A
kisülés négy elektróda között jön létre, a két katód és a
két anód aktív felülete egy közös hengerpaláston helyezkedik
el. A görbült katódfelületek a kisülés tengelye irányába
fókuszálják a katódból kilépő, majd annak környezetében
felgyorsult elektronokat, ahol az ionizációs forrás
éles csúcsot mutat. Az erős fókuszálás a geometriai
viszonyok mellett a szegmentált üreges katódú kisülések
nagy égési feszültségével (400-1000 V) magyarázható. Az
ennek megfelelő energiákra felgyorsult elektronok szabad
úthossza igen nagy (összemérhető a katódüreg átmérőjével),
ugyanis az ütközési hatáskeresztmetszetek ebben
az energiatartományban már lényegesen kisebbek a
maximális értékeknél. A szimulációkkal megmutattuk,
hogy a szabályozott feszültségű üreges katódú kisülésben
a nagyobb feszültséget a töltéshordozók veszteségének
növekedése eredményezi, ilyenkor növekszik az
ionizáció a gyors elektronok hatására, továbbá közvetlen
bizonyítékát tudtuk adni a kisülésben az oszcilláló elektronok
jelenlétének [21].
Komplex kisülések önkonzisztens leírását teszik lehetővé
a részecskeszimulációs (Monte Carlo szimulációt)
és hidrodinamikai leírást egyesítő 1- és 2-dimenziós
önkonzisztens, úgynevezett hibrid modellek. (Önkonzisztens
leírás alatt itt azt értjük, hogy a töltött részecskék
olyan elektromos térben mozognak, amelyet a
saját töltéssűrűségük is befolyásol.) Hibrid modellek alkalmazásával
sikeresen vizsgáltuk gázkisülések különböző
jelenségeit: öngerjesztett oszcillációkat, az elektródakonfiguráció
hatását a kisülés jellemzőire, az üreges
katódú kisülések létrejöttét, a katódporlás jelenségét, a
kisülési plazmák fénykibocsátásának térbeli eloszlását
[25], a gázkisülések tranzienseit [26], illetve a He-Au+ lézer
gerjesztési viszonyait [27].
Egy további kutatási területként megemlítendő a folyadékfelületen
létrehozott atmoszférikus nyomású plazma
felhasználása környezetvédelmi analitikai célokra [28,
29]: az elektrolitkatódos atmoszférikus nyomású ködfénykisülés
(Electrolyte Cathode Atmospheric Glow Discharge,
ELCAD) a vizek nehézfémtartalmának közvetlen
meghatározására használható. Az utóbbi években részletesen
foglalkoztunk ezen speciális kisülés működési mechanizmusával.
Értelmeztük az összetétel hatását a katódporlásra,
vizsgáltuk a gáz- és elektronhőmérséklet-eloszlásokat,
valamint a kisülés gerjesztési viszonyait. E kutatások
gyakorlati alkalmazásaként szubnanogramm érzékenységű
többelemes fémdetektort építettünk kapilláris
elrendezésű ELCAD-ban.
a részecske
kinetikus energiája és R01 a (0,1) intervallumon
egyenletes eloszlású véletlen számot jelöl [24].
A szabad úthossz befutása után a részecske különböző
ütközési folyamatokban vehet részt, az egyes folyamatok
bekövetkezésének valószínűsége arányos az ütközési
energiánál vett megfelelő hatáskeresztmetszet-értékekkel.
Ez a módszer azokban az esetekben használható, amikor
(az alacsony ionizációs foknak köszönhetően) elhanyagolható
a töltött részecskék közötti direkt kölcsönhatás
(pl. elektron-elektron ütközések), és így csak a töltött
részecskék (elektronok vagy ionok) transzportját kell
leírni a semleges háttérgázban. A szimuláció természetesen
lehetőséget ad arra, hogy az ionizációs folyamatokban
keletkező újabb elektronokat is kövessük, így megfigyelhetjük
a katódból induló elektronok által keltett
elektronlavinákat. A 7. ábra erre mutat egy példát - az
ábrán 2,5 mbar nyomású héliumgázban, L = 1 cm elektródatávolság
és U = 500 V feszültség esetén láthatjuk egy
elektronlavina Monte Carlo szimulációval kapott képét.
A szimulációkkal vizsgálható a kisülések időbeli felépülése,
illetve a töltött részecskék kinetikája bonyolultabb
elektródakonfigurációk esetében is. A 8. ábra egy
lézercélú szegmentált üreges katódú kisülés [15] keresztmetszetében
szemlélteti az ionizáció térbeli eloszlását. A
kisülés négy elektróda között jön létre, a két katód és a
két anód aktív felülete egy közös hengerpaláston helyezkedik
el. A görbült katódfelületek a kisülés tengelye irányába
fókuszálják a katódból kilépő, majd annak környezetében
felgyorsult elektronokat, ahol az ionizációs forrás
éles csúcsot mutat. Az erős fókuszálás a geometriai
viszonyok mellett a szegmentált üreges katódú kisülések
nagy égési feszültségével (400-1000 V) magyarázható. Az
ennek megfelelő energiákra felgyorsult elektronok szabad
úthossza igen nagy (összemérhető a katódüreg átmérőjével),
ugyanis az ütközési hatáskeresztmetszetek ebben
az energiatartományban már lényegesen kisebbek a
maximális értékeknél. A szimulációkkal megmutattuk,
hogy a szabályozott feszültségű üreges katódú kisülésben
a nagyobb feszültséget a töltéshordozók veszteségének
növekedése eredményezi, ilyenkor növekszik az
ionizáció a gyors elektronok hatására, továbbá közvetlen
bizonyítékát tudtuk adni a kisülésben az oszcilláló elektronok
jelenlétének [21].
Komplex kisülések önkonzisztens leírását teszik lehetővé
a részecskeszimulációs (Monte Carlo szimulációt)
és hidrodinamikai leírást egyesítő 1- és 2-dimenziós
önkonzisztens, úgynevezett hibrid modellek. (Önkonzisztens
leírás alatt itt azt értjük, hogy a töltött részecskék
olyan elektromos térben mozognak, amelyet a
saját töltéssűrűségük is befolyásol.) Hibrid modellek alkalmazásával
sikeresen vizsgáltuk gázkisülések különböző
jelenségeit: öngerjesztett oszcillációkat, az elektródakonfiguráció
hatását a kisülés jellemzőire, az üreges
katódú kisülések létrejöttét, a katódporlás jelenségét, a
kisülési plazmák fénykibocsátásának térbeli eloszlását
[25], a gázkisülések tranzienseit [26], illetve a He-Au+ lézer
gerjesztési viszonyait [27].
Egy további kutatási területként megemlítendő a folyadékfelületen
létrehozott atmoszférikus nyomású plazma
felhasználása környezetvédelmi analitikai célokra [28,
29]: az elektrolitkatódos atmoszférikus nyomású ködfénykisülés
(Electrolyte Cathode Atmospheric Glow Discharge,
ELCAD) a vizek nehézfémtartalmának közvetlen
meghatározására használható. Az utóbbi években részletesen
foglalkoztunk ezen speciális kisülés működési mechanizmusával.
Értelmeztük az összetétel hatását a katódporlásra,
vizsgáltuk a gáz- és elektronhőmérséklet-eloszlásokat,
valamint a kisülés gerjesztési viszonyait. E kutatások
gyakorlati alkalmazásaként szubnanogramm érzékenységű
többelemes fémdetektort építettünk kapilláris
elrendezésű ELCAD-ban.

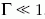 . Egyes
nemklasszikus plazmákban viszont a kölcsönhatási (potenciális)
energia (lényegesen) nagyobb lehet a kinetikus
energiánál, és ekkor erősen csatolt plazmákról beszélünk,
amelyekre
. Egyes
nemklasszikus plazmákban viszont a kölcsönhatási (potenciális)
energia (lényegesen) nagyobb lehet a kinetikus
energiánál, és ekkor erősen csatolt plazmákról beszélünk,
amelyekre 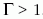 . Erősen csatolt plazmákra példa a
neutroncsillagok köpenyében, fehér törpecsillagokban,
óriásbolygók belsejében található anyagállapot, ahol a
teljesen ionizált atomok iontörzsei erősen csatolt rendszert
alkotnak, miközben a degenerált állapotú elektronok
egy semlegesítő hátteret képeznek. Mesterségesen
létrehozott erősen csatolt plazmákra példaként említhetők
a csapdákban tárolt ionok, amelyek esetében a hőmérséklet
igen alacsony lehet, és így a rendszerek kristályos
állapotba kerülhetnek [30].
A plazmák speciális (és egyre inkább az érdeklődés
középpontjába kerülő) fajtáját képviselik a komplex plazmák,
amelyekben az elektronok, ionok és semleges gázatomok
(molekulák) mellett nanométer-mikrométer méretű
részecskék is jelen vannak. Ilyen rendszerekre asztrofizikai
példaként a csillagközi por, az üstökösök csóvája,
a Szaturnusz és az Uránusz gyűrűi említhetők. A porrészecskék
az ultraibolya sugárzás miatti elektronemisszió,
vagy nagyenergiájú részecskékkel való ütközések
hatására elektromosan töltötté válnak, így a plazma többi
összetevőjével kölcsönhatásba kerülnek, és azokhoz hasonlóan
reagálnak a külső elektromos és mágneses térre.
Mivel a plazma egyéb összetevőihez képest az igen nagy
méretű porrészecskék nagy töltést vehetnek fel, a porrészecskék
gyakran erősen csatolt rendszert alkotnak, plazmakristályok
keletkezhetnek, amint azt laboratóriumi kísérletekben
is megmutatták.
Az erősen csatolt plazmák területén végzett munkánk
Coulomb- és Yukawa-kölcsönhatási potenciállal jellemezhető
sokrészecske-rendszerekben lejátszódó jelenségek
nyomon követésére, különleges körülmények között
található anyagoktulajdonságainakleírására irányul. A
statikus termodinamikai jellemzők mellett a szimulációkkal
vizsgáltuk az erősen csatolt rendszereket alkotó részecskék
lokalizációját [31], valamint a rendszerek kollektív
(dinamikus) jelenségeit [32, 33]. Nemegyensúlyi molekuladinamikai
szimulációs módszerekkel meghatároztuk
a rendszerek egyes transzportjellemzőit (nyíró viszkozitást
és hővezetési együtthatót) [34, 35].
. Erősen csatolt plazmákra példa a
neutroncsillagok köpenyében, fehér törpecsillagokban,
óriásbolygók belsejében található anyagállapot, ahol a
teljesen ionizált atomok iontörzsei erősen csatolt rendszert
alkotnak, miközben a degenerált állapotú elektronok
egy semlegesítő hátteret képeznek. Mesterségesen
létrehozott erősen csatolt plazmákra példaként említhetők
a csapdákban tárolt ionok, amelyek esetében a hőmérséklet
igen alacsony lehet, és így a rendszerek kristályos
állapotba kerülhetnek [30].
A plazmák speciális (és egyre inkább az érdeklődés
középpontjába kerülő) fajtáját képviselik a komplex plazmák,
amelyekben az elektronok, ionok és semleges gázatomok
(molekulák) mellett nanométer-mikrométer méretű
részecskék is jelen vannak. Ilyen rendszerekre asztrofizikai
példaként a csillagközi por, az üstökösök csóvája,
a Szaturnusz és az Uránusz gyűrűi említhetők. A porrészecskék
az ultraibolya sugárzás miatti elektronemisszió,
vagy nagyenergiájú részecskékkel való ütközések
hatására elektromosan töltötté válnak, így a plazma többi
összetevőjével kölcsönhatásba kerülnek, és azokhoz hasonlóan
reagálnak a külső elektromos és mágneses térre.
Mivel a plazma egyéb összetevőihez képest az igen nagy
méretű porrészecskék nagy töltést vehetnek fel, a porrészecskék
gyakran erősen csatolt rendszert alkotnak, plazmakristályok
keletkezhetnek, amint azt laboratóriumi kísérletekben
is megmutatták.
Az erősen csatolt plazmák területén végzett munkánk
Coulomb- és Yukawa-kölcsönhatási potenciállal jellemezhető
sokrészecske-rendszerekben lejátszódó jelenségek
nyomon követésére, különleges körülmények között
található anyagoktulajdonságainakleírására irányul. A
statikus termodinamikai jellemzők mellett a szimulációkkal
vizsgáltuk az erősen csatolt rendszereket alkotó részecskék
lokalizációját [31], valamint a rendszerek kollektív
(dinamikus) jelenségeit [32, 33]. Nemegyensúlyi molekuladinamikai
szimulációs módszerekkel meghatároztuk
a rendszerek egyes transzportjellemzőit (nyíró viszkozitást
és hővezetési együtthatót) [34, 35].
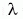 = 224 nm)
lézer kutatása és praktikus lézer fejlesztése a legfontosabb
feladat, elsősorban Raman-spektroszkópiai vizsgálatokhoz.
Az elektrolitkatódos atmoszférikus nyomású kisülés
esetén az egyre nagyobb érzékenység (kisebb kimutatható
szennyezőkoncentráció) elérésén dolgozunk.
Az alacsony nyomású gázkisülések (kis ionizáltsági
fokú plazmáinak) területén legfontosabb az önkonzisztens,
első elvekből kiinduló modellezési eljárások fejlesztése.
Elsődlegesen a PIC (Particle-In-Cell) szimulációs
módszerek [36] továbbfejlesztésére koncentrálunk. A
PIC-módszer a töltött részecskék mozgását a klasszikus
mozgásegyenlettel írja le, a részecskékre ható erő az
elektromos térerősségből adódik, ezt pedig a töltött
részecskék jelenléte és az elektródákra kapcsolt potenciál
határozza meg. A mozgásegyenlet és a Poisson-egyenlet
együttes megoldása biztosítja az eredmények
önkonzisztens voltát. Egy évtizeddel ezelőtt csak az
akkori szuperszámítógépek adtak lehetőséget ilyen modelleken
alapuló számításokra, a módszer szélesebb
körű elterjedése a számítástechnikai háttér igen gyors
fejlődésének köszönhető.
Az erősen csatolt plazmák vizsgálata egy új, dinamikusan
fejlődő terület. Itt elsősorban a Coulomb- és Yukawa-kölcsönhatási
potenciállal jellemezhető sokrészecskerendszereket
kutatjuk. Az eredményeknek a laboratóriumban
létrehozott állapotokvizsgálata mellett asztrofizikai
jelentőségük is van.
A jövőben tervezett kutatási témáink elsősorban alapkutatás-
motiváltak, de az itt szerezhető ismeretek az alkalmazások szempontjából
is hasznosak lehetnek .
= 224 nm)
lézer kutatása és praktikus lézer fejlesztése a legfontosabb
feladat, elsősorban Raman-spektroszkópiai vizsgálatokhoz.
Az elektrolitkatódos atmoszférikus nyomású kisülés
esetén az egyre nagyobb érzékenység (kisebb kimutatható
szennyezőkoncentráció) elérésén dolgozunk.
Az alacsony nyomású gázkisülések (kis ionizáltsági
fokú plazmáinak) területén legfontosabb az önkonzisztens,
első elvekből kiinduló modellezési eljárások fejlesztése.
Elsődlegesen a PIC (Particle-In-Cell) szimulációs
módszerek [36] továbbfejlesztésére koncentrálunk. A
PIC-módszer a töltött részecskék mozgását a klasszikus
mozgásegyenlettel írja le, a részecskékre ható erő az
elektromos térerősségből adódik, ezt pedig a töltött
részecskék jelenléte és az elektródákra kapcsolt potenciál
határozza meg. A mozgásegyenlet és a Poisson-egyenlet
együttes megoldása biztosítja az eredmények
önkonzisztens voltát. Egy évtizeddel ezelőtt csak az
akkori szuperszámítógépek adtak lehetőséget ilyen modelleken
alapuló számításokra, a módszer szélesebb
körű elterjedése a számítástechnikai háttér igen gyors
fejlődésének köszönhető.
Az erősen csatolt plazmák vizsgálata egy új, dinamikusan
fejlődő terület. Itt elsősorban a Coulomb- és Yukawa-kölcsönhatási
potenciállal jellemezhető sokrészecskerendszereket
kutatjuk. Az eredményeknek a laboratóriumban
létrehozott állapotokvizsgálata mellett asztrofizikai
jelentőségük is van.
A jövőben tervezett kutatási témáink elsősorban alapkutatás-
motiváltak, de az itt szerezhető ismeretek az alkalmazások szempontjából
is hasznosak lehetnek .