Fizikai Szemle honlap |
Tartalomjegyzék |
(G. P. )
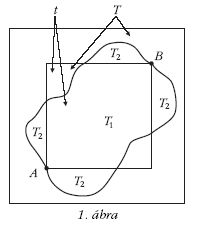 Jelöljük az 1. ábrán látható módon a kisebb négyzet területét
t -vel, a nagyobb (befoglaló) négyzetét T-vel, a cérnaszál
által körülfogott, de a
kisebb négyzeten kívül eső
teljes (4 darabból álló) területet
T2-vel, a kis négyzeten is
és a cérnaszálon is belül eső
rész területét pedig T1-gyel!
Ha a cérnaszálon és a kis
négyzeten kívül eső T - t - T2
nagyságú felületet
Jelöljük az 1. ábrán látható módon a kisebb négyzet területét
t -vel, a nagyobb (befoglaló) négyzetét T-vel, a cérnaszál
által körülfogott, de a
kisebb négyzeten kívül eső
teljes (4 darabból álló) területet
T2-vel, a kis négyzeten is
és a cérnaszálon is belül eső
rész területét pedig T1-gyel!
Ha a cérnaszálon és a kis
négyzeten kívül eső T - t - T2
nagyságú felületet 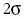 felületi
feszültségű hártyával borítjuk,
a kis négyzeten belüli,
de a cérnahurkon kívül eső
t - T1 nagyságú felületet pedig
felületi
feszültségű hártyával borítjuk,
a kis négyzeten belüli,
de a cérnahurkon kívül eső
t - T1 nagyságú felületet pedig 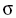 felületi feszültségű hártyával,
akkor a rendszer teljes (felületi) energiája:
felületi feszültségű hártyával,
akkor a rendszer teljes (felületi) energiája:
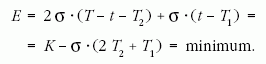
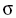 állandó volta
miatt akkor a legkisebb, amikor
állandó volta
miatt akkor a legkisebb, amikor
T1 + 2 T2
A szappanhártyás feladat megoldása tehát valóban egyenértékű a 136. problémában szereplő (a kis négyzeten kívül a benti négyzetméterárnál kétszer drágább telek) ároptimalizálási feladattal.1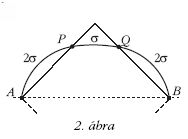 Az optimumfeladatot azzal a mellékfeltétellel kell megoldanunk,
hogy a cérnaszál két pontban (az 1. ábrán A és
B) rögzített, hossza pedig a négyzet kerületével egyezik
meg. A vizsgálandó feladat az AB egyenesre szimmetrikus,
elegendő tehát a "félmegoldással" foglalkozzunk. A kis
négyzet oldalának hosszát egységnyinek választhatjuk (az
eredeti problémában ez 25 m, a kerítés teljes hossza 100 m
volt, ezeknek megfelelő megoldás arányos nagyítással
kapható az "egységnégyzetből").
Tekintsük tehát a 2. ábrán látható elrendezést:
mindkét végén rögzített (hajlékony
és nyújthatatlan) cérnaszálat,
amelyre az AP és
QB görbeszakaszokon kívülről
Az optimumfeladatot azzal a mellékfeltétellel kell megoldanunk,
hogy a cérnaszál két pontban (az 1. ábrán A és
B) rögzített, hossza pedig a négyzet kerületével egyezik
meg. A vizsgálandó feladat az AB egyenesre szimmetrikus,
elegendő tehát a "félmegoldással" foglalkozzunk. A kis
négyzet oldalának hosszát egységnyinek választhatjuk (az
eredeti problémában ez 25 m, a kerítés teljes hossza 100 m
volt, ezeknek megfelelő megoldás arányos nagyítással
kapható az "egységnégyzetből").
Tekintsük tehát a 2. ábrán látható elrendezést:
mindkét végén rögzített (hajlékony
és nyújthatatlan) cérnaszálat,
amelyre az AP és
QB görbeszakaszokon kívülről
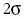 felületi feszültségű
hártya feszül, a PQ ív mentén viszont csak
felületi feszültségű
hártya feszül, a PQ ív mentén viszont csak 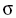 a hártya felületi
feszültsége. A cérnaszál hossza A és B között ugyanakkora,
mint a négyzet fél kerülete, vagyis 2 egységnyi.
Vizsgáljuk most a problémát az erők egyensúlya szempontjából!
A cérnaszálat mindenhol ugyanakkora (F)
nagyságú erő feszíti; ellenkező esetben a szál valamely
darabkája elmozdulna az érintője irányában. Másrészt a
szál az érintőre merőlegesen sem mozdul el, ez pedig akkor
teljesül, ha a felületi feszültségből származó (hosszegységenként
a hártya felületi
feszültsége. A cérnaszál hossza A és B között ugyanakkora,
mint a négyzet fél kerülete, vagyis 2 egységnyi.
Vizsgáljuk most a problémát az erők egyensúlya szempontjából!
A cérnaszálat mindenhol ugyanakkora (F)
nagyságú erő feszíti; ellenkező esetben a szál valamely
darabkája elmozdulna az érintője irányában. Másrészt a
szál az érintőre merőlegesen sem mozdul el, ez pedig akkor
teljesül, ha a felületi feszültségből származó (hosszegységenként
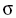 , illetve
, illetve 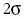 nagyságú) erő egyensúlyt tart a
szál görbültségéből adódó, hosszegységenként F · G
nagyságú erővel. (G a szál görbülete, a simulókör görbületi
sugarának reciproka.)
nagyságú) erő egyensúlyt tart a
szál görbültségéből adódó, hosszegységenként F · G
nagyságú erővel. (G a szál görbülete, a simulókör görbületi
sugarának reciproka.)
 Az elmondottak alapján
az energiaminimumot szolgáltató
"optimális megoldásban"
a cérnaszál görbülete
szakaszonként állandó, tehát
körívekből áll, de a felületi
feszültségek (az eredeti feladatban
a telekárak) különbözősége
miatt az AP és QB
körívek sugara fele akkora,
mint a PQ körívé. A P és a Q
pontokban - ugyancsak az erőegyensúly miatt - a körívek
törésmentesen, folytonosan változó érintővel csatlakoznak
egymáshoz, továbbá a három körív teljes hossza
2 egység kell legyen. Ezek a megszorítások már - elemi
geometriai összefüggésekkel - meghatározzák a körívek
sugarát és az ívek középponti szögeit.
Az elmondottak alapján
az energiaminimumot szolgáltató
"optimális megoldásban"
a cérnaszál görbülete
szakaszonként állandó, tehát
körívekből áll, de a felületi
feszültségek (az eredeti feladatban
a telekárak) különbözősége
miatt az AP és QB
körívek sugara fele akkora,
mint a PQ körívé. A P és a Q
pontokban - ugyancsak az erőegyensúly miatt - a körívek
törésmentesen, folytonosan változó érintővel csatlakoznak
egymáshoz, továbbá a három körív teljes hossza
2 egység kell legyen. Ezek a megszorítások már - elemi
geometriai összefüggésekkel - meghatározzák a körívek
sugarát és az ívek középponti szögeit.
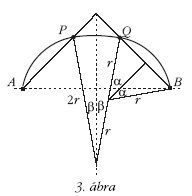
A 3. ábra jelöléseit követve felírhatjuk, hogy
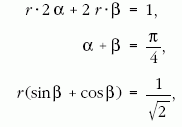
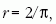 ,
valamint
,
valamint 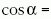
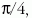 ,
azaz
,
azaz 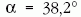 és
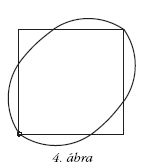
és 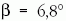 adódik. A teljes megoldás
vázlatos rajza a 4. ábrán látható.
adódik. A teljes megoldás
vázlatos rajza a 4. ábrán látható.
 Megjegyzés: A megoldás során
(a feladat szimmetriájára gondolva)
hallgatólagosan feltettük, hogy
a cérnaszál (illetve a 136. problémánál
a kerítés) nemcsak az AB
egyenesre, hanem annak felező merőlegesére is szimmetrikus,
vagyis hogy a kerület összesen 6 körívből
rakható össze. Ez egyáltalán nem nyilvánvaló! Ha egy
szívószál két végére egy-egy szappanbuborékot illesztünk,
a pontosan egyforma sugarú buborékok esete
egyensúlyi állapotnak felel meg, azonban ez az állapot
instabil, az összenergiának nem minimuma. A stabil
egyensúlyi állapotban (energiaminimumban) az egyik
buborék sugara nullává válik, s a gáz teljes mennyisége
a másik buborékba kerül, tehát az elrendeződés aszimmetrikus
lesz, jóllehet a probléma tükörszimmetrikus!
Hasonló módon elképzelhető lenne, hogy a 3. ábrán
látható szimmetrikus állapot egyensúlyi ugyan, de instabil,
és a stabil egyensúly aszimmetrikus: a P és az A
pont egybeesik, a teljes határgörbe pedig nem 6, hanem
csak 4 körívből áll. Ténylegesen nem ez a helyzet, de a
megnyugtató megoldásnak ezen lehetőség vizsgálata is
részét képezi.
Megjegyzés: A megoldás során
(a feladat szimmetriájára gondolva)
hallgatólagosan feltettük, hogy
a cérnaszál (illetve a 136. problémánál
a kerítés) nemcsak az AB
egyenesre, hanem annak felező merőlegesére is szimmetrikus,
vagyis hogy a kerület összesen 6 körívből
rakható össze. Ez egyáltalán nem nyilvánvaló! Ha egy
szívószál két végére egy-egy szappanbuborékot illesztünk,
a pontosan egyforma sugarú buborékok esete
egyensúlyi állapotnak felel meg, azonban ez az állapot
instabil, az összenergiának nem minimuma. A stabil
egyensúlyi állapotban (energiaminimumban) az egyik
buborék sugara nullává válik, s a gáz teljes mennyisége
a másik buborékba kerül, tehát az elrendeződés aszimmetrikus
lesz, jóllehet a probléma tükörszimmetrikus!
Hasonló módon elképzelhető lenne, hogy a 3. ábrán
látható szimmetrikus állapot egyensúlyi ugyan, de instabil,
és a stabil egyensúly aszimmetrikus: a P és az A
pont egybeesik, a teljes határgörbe pedig nem 6, hanem
csak 4 körívből áll. Ténylegesen nem ez a helyzet, de a
megnyugtató megoldásnak ezen lehetőség vizsgálata is
részét képezi.
(G. P. )
__________________________________
1 Az érdekes fizikai-közgazdasági ikerfeladványt - a problémát eredetileg megfogalmazó - V. Sedach (Seattle, USA) más geometriai feltétellel adta meg egy internetes versenyen. A Négyszögletes kerék hangulatához közelebb álló változatot Nagy Győző (Budapest) dolgozta ki.