Fizikai Szemle 2006/2. 61.o.
A RELATIVITÁSELMÉLET TANÍTÁSÁRÓL
Hraskó Péter
Pécsi Tudományegyetem
Elméleti Fizika Tanszék
Az utóbbi tíz évben sokat foglalkoztam a relativitáselmélet
tanításával és népszerűsítésével, ezért az elméletet a korábbinál
alaposabban át kellett gondolnom. Eközben több
olyan fogalom revideálására is rákényszerültem, amelyekben
azelőtt semmi kivetnivalót sem találtam. Közöttük van
a mozgási tömeg, amely bekerült az emelt szintű érettségi
tételei közé. Erről a fogalomról lesz szó az alábbiakban.
A speciális relativitáselmélet egyik váratlan következménye
az, hogy minél nagyobb sebességgel mozog egy
test, annál nehezebb tovább gyorsítani. Pontosan ez
lenne a helyzet akkor, ha a testek tömege nőne a sebesség
növelésekor. De a gondolatmenet, amellyel a relativitáselméletben
eljutunk ehhez a következtetéshez, világosan
mutatja, hogy a jelenség oka nem a tömeg megnövekedése,
hanem az idodilatáció.
Képzeljünk el egy rakétát, amelyben automata adagoló
biztosítja, hogy a hajtóműben minden másodpercben
pontosan ugyanakkora legyen az üzemanyag-fogyasztás,
és vizsgáljuk a rakéta mozgását a pályájának egy viszonylag
rövid szakaszán, amelyen az üzemanyag elhasználódásából
származó tömegcsökkenés elhanyagolható a
rakéta össztömegéhez képest. A newtoni mechanika szerint
ilyen körülmények között a rakéta konstans gyorsulással
fog mozogni. A tolóerő ugyanis állandó, és az

képletnek megfelelően a sebesség időegységre eső növekedése is konstans:

A relativitáselmélet szerint azonban a külső megfigyelő
számára a gyorsulás egyre kisebb és kisebb lesz, mert
az adagoló berendezés az űrhajóbeli sajátidő ritmusában
adagolja az üzemanyagot, és ez a sajátidő a
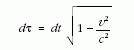
képletnek megfelelően annál lassabban telik, minél nagyobb az űrhajó sebessége.
Kis sebességeknél 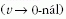 a newtoni mechanika a
relativitáselméletben is érvényes, ezért az űrhajóhoz képest
az (1) képlet igaz marad, csak időn természetesen az
űrhajóbeli
a newtoni mechanika a
relativitáselméletben is érvényes, ezért az űrhajóhoz képest
az (1) képlet igaz marad, csak időn természetesen az
űrhajóbeli 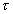 sajátidőt kell érteni:
sajátidőt kell érteni:

Ennek következtében az űrhajó gyorsulása önmagához
képest továbbra is a konstans F/m-mel egyenlő. A földi
megfigyelő által észlelt gyorsulást úgy kapjuk, hogy a (3)
képletben a 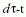 kifejezzük a földi időn keresztül:
kifejezzük a földi időn keresztül:
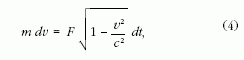
amelyből
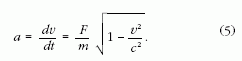
Ez a képlet valóban azt mutatja, hogy a sebesség növeke-
désével a gyorsítás hatásossága csökken.
Az (5)-ben az idődilatációnak csak a gyorsulás okára
(a gyorsító erő teljesítményére) kifejtett hatását vettük
figyelembe. Nézzük most meg, mi lesz az idődilatáció
hatása a sebességnövekedésre.
Jelöljük I '-vel azt az inerciarendszert, amelyhez képest
a rakéta a t pillanatban éppen nyugszik. A rakéta
azonban I '-höz képest is gyorsul, ezért a nyugalom állapota
csak egy matematikai pillanatig tart, és a t időpillanatot
követő rövid 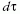 sajátidő-intervallumban a rakéta
I '-hez viszonyítva megtesz valamekkora - mondjuk dl0 -
utat. Ezalatt a rakéta sebessége I '-ben (vagyis "önmagához
képest") valamilyen dv'-vel nő meg. Mekkora dv
sebességnövekedésként fog ez megjelenni az I -beli megfigyelők
számára?
Abban az I inerciarendszerben, amelyből a rakéta
mozgását figyeljük, a dl0-nak a Lorentz-kontrakció szerint
sajátidő-intervallumban a rakéta
I '-hez viszonyítva megtesz valamekkora - mondjuk dl0 -
utat. Ezalatt a rakéta sebessége I '-ben (vagyis "önmagához
képest") valamilyen dv'-vel nő meg. Mekkora dv
sebességnövekedésként fog ez megjelenni az I -beli megfigyelők
számára?
Abban az I inerciarendszerben, amelyből a rakéta
mozgását figyeljük, a dl0-nak a Lorentz-kontrakció szerint
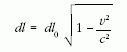
távolság, a 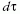 sajátidő-intervallumnak pedig
sajátidő-intervallumnak pedig
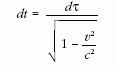
időintervallum felel meg. Logikus feltételezni, hogy dv
ugyanúgy aránylik a dv'-höz, ahogy dl /dt aránylik a
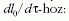 :
:
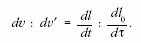
De a Lorentz-kontrakció és az idődilatáció előbbi képletei
szerint ez az arány (1-v 2/c2)-tel egyenlő, ezért
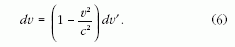
A (3) képlet tehát további pontosításra szorul, a dv-t
dv'-vel kell helyettesíteni benne:

Ha most itt dv'-t és 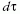 -t kifejezzük a földi megfigyelők által
észlelt dv-n és dt-n keresztül, az űrhajó gyorsulására az
-t kifejezzük a földi megfigyelők által
észlelt dv-n és dt-n keresztül, az űrhajó gyorsulására az
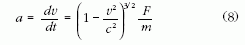
képletet kapjuk.
Ezt a képletet - a könnyebb érthetőség kedvéért - a rakéta
példáján vezettük le. A nagy sebességgel mozgó testek
gyorsulását azonban töltött részecskék elektromágneses
térben történő mozgásánál figyelték meg (Kaufmann-kísérlet,
1901-1902). Érvényes-e (8) ebben az esetben is?
A legegyszerűbb eset az, amikor a Q töltésű részecske a
konstans E elektromos térrel párhuzamosan mozog. Ekkor
F = QE. De ebben az esetben a (7) képletben egy
újabb módosítást kell végrehajtani. Az elektromos (és a
mágneses) tér komponensei ugyanis általában megváltoznak,
amikor új inerciarendszerre térünk át, ezért (7)-ben
F-et az I '-beli F' = QE'-vel kell helyettesíteni. Abban a
speciális esetben azonban, amikor az inerciarendszerek
relatív sebessége párhuzamos az elektromos térrel, az
elektromos tér mindkét inerciarendszerben ugyanakkora:
E' = E. Így F' = F, (7)-en semmit sem kell változtatni, és
a töltött részecskék gyorsulását is (8) határozza meg1.
A (8) képlet korrekt, de az egyszerűsített gondolatmenet,
amivel megkaptuk, tartalmaz egy olyan lépést, amelyet
talán nem mindenki tartana meggyőzőnek (a (6) indoklására
gondolok2). Az egyszerűsítés azonban olyan,
hogy nem hamisítja meg, hanem inkább kiemeli a jelenség
lényegét: Azért nehezebb a nagy sebességgel mozgó
testet tovább gyorsítani, mert az idődilatáció egyre hatékonyabbá
válik.
A gondolatmenetben az idődilatáción kívül a Lorentz-kontrakció
is szerephez jutott, ezért a fenti indokláshoz
a Lorentz-kontrakciót is hozzá lehet tenni. Magának a
Lorentz-kontrakciónak a képletét azonban le lehet vezetni
egyedül az idődilatációból (ld. a Függeléket), ezért
úgy gondolom, hogy elég, ha csak az idődilatációra
hivatkozunk.
Ismeretes, hogy a relativitáselméletben a v sebességgel
mozgó test mozgási energiáját a
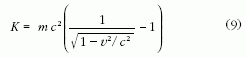
képlet határozza meg. Ha ezt összehasonlítjuk a newtoni fizika
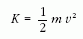
képletével, láthatjuk, hogy a relativitáselmélet szerint a
mozgási energia a sebesség növelésekor gyorsabban nő,
mint a newtoni fizika szerint: Amikor v tart a fénysebességhez,
a két mozgási energia aránya végtelenhez tart.
Ez a tény egyenes következménye annak, hogy a nagyobb
sebességgel mozgó testet nehezebb gyorsítani. A
mozgási energia ugyanis a gyorsító erő munkájának rovására
növekszik (dK = Fdx), és egy adott sebességet nyilván
hosszabb úton lehet csak elérni, ha a sebesség további
növelése egyre nehezebbé válik.
Néhány alkalommal találkoztam olyan ellenvetéssel,
hogy azért kell léteznie relativisztikus tömegnövekedésnek,
mert a mozgó test nagyobb gravitációs hatást fejt ki,
mint a nyugvó, és ha a tömeg mindkét esetben ugyanaz
lenne, a gravitációs hatás se lehetne más.
Ez az ellenvetés azért hibás, mert a relativitáselmélet
szerint (és itt már az általános relativitáselméletről van szó)
a gravitációs hatás forrása nem a tömeg, hanem az energia
(pontosabban az energia-impulzus-tenzor, de ehhez a legfontosabb
járulékot az energia adja). A mozgó test gravitációs
hatása tehát valóban nagyobb a nyugvóénál, de nem a
tömeg, hanem az energia megnövekedése miatt.
Mindezek alapján az a javaslatom, hogy a "mozgási
tömeg" és a "relativisztikus tömegnövekedés" kifejezéseket
ne használjuk, mert hamis magyarázatot sugallnak
arra, hogy miért nehezebb a testeket tovább gyorsítani,
amikor már gyorsan mozognak. Ha ezt elfogadjuk, akkor
persze a "nyugalmi tömeg" terminusra sincs szükség. A
"nyugalmi energia" kifejezést azonban, amely a "belső
energia" szinonimája, kifejezetten célszerű használni,
mert explicite utal arra, hogy a belső energia a nyugvó
test energiájával azonos.
A fotonok zérus tömegű objektumok, de nagyon gyakran
ezt úgy értik, hogy csak a nyugalmi tömegük nulla, a
mozgási tömegük h /c2-tel egyenlő. Arról, hogy ez milyen
hibás következtetésekre vezet, korábban már részletesen
írtam3, ezért az ottani érveimet most nem ismétlem meg.
A "mozgási tömeg" elnevezés az irodalomban nagyon
elterjedt, de vannak figyelemre méltó kivételek. A Speciális
és általános relativitás elmélete című könyvében Einstein
nem használja ezt a kifejezést. A Landau-Lifsic sorozatban
sem fordul elő, de hiánya a tíz kötetben sehol sem
okoz problémát. W.G. Dixon kompromisszumos megoldást
választott4: Az
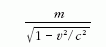
mennyiséget "látszólagos tömegnek" (apparent mass)
hívja, és m-re megtartja a nyugalmi tömeg nevet.
Hogyan került be a fizikába az az elképzelés, hogy a
tömeg esetleg függhet a sebességtől? Az 1880-as évek
elején J.J. Thomson kezdte el alkalmazni a Maxwell-egyenleteket
az anyag tulajdonságainak a vizsgálatára. A
kutatás, amelybe sokan bekapcsolódtak, egyik fontos
következtetése az volt, hogy mozgó töltés elektromágneses
terében annál nagyobb térenergia van felhalmozva,
minél gyorsabban mozog a test, és ez arra vezet, hogy
egy töltött testet annál nehezebb gyorsítani, minél nagyobb
a sebessége. Hamar szokásossá vált ezt az eredményt
úgy fogalmazni, hogy a töltött testek tömege nő a
sebességgel.
A XIX. század utolsó éveiben J. Larmor és W. Wien
mondta ki azt a hipotézist, hogy mivel az anyag elektromosan
töltött alkotórészekből áll, a tömeg (az elektromosan
semleges testek tömege is!) esetleg tisztán az elektromágneses
térenergia hatásának a megnyilvánulása (a
tömeg elektromágneses elmélete).
W. Kaufmann már említett kísérleteit ezek az elképzelések
inspirálták. A kísérletek igazolták, hogy az elektronokat
annál nehezebb gyorsítani, minél nagyobb a sebességük,
és a már megszokott szóhasználattal ezt tömegnövekedésként
fogták fel. A tömeg elektromágneses elméletéről
azonban hamar kiderült, hogy nem tartható, mert
az elektromágneses kölcsönhatás önmagában nem tud
stabil anyagot létrehozni, a relativitáselmélet viszont természetes
magyarázatot kínál Kaufmann eredményeire. Ez
a magyarázat nem a tömegnövekedésen, hanem a Lorentz-
transzformáció sajátosságain alapul. Ennek ellenére
ma is sokan gondolják úgy, hogy a relativitáselmélet is
tömegnövekedésre vezeti vissza azt, hogy a gyorsan
mozgó elektronokat nehezebb tovább gyorsítani, mint a
lassan mozgókat.
Függelék
1) A (6) levezetése a sebességösszeadás képletéből:
Mozogjon az I' inerciarendszer V konstans sebességgel az
I inerciarendszerhez képest mondjuk az x-tengely
mentén. Figyeljünk meg mindkét inerciarendszerből egy
ugyancsak x mentén (változó sebességgel) mozgó objektumot.
Az objektum sebessége a két inerciarendszerhez
képest természetesen nem lesz ugyanaz. Ha a pályájának
egy adott pontjában az objektum I'-höz viszonyított sebessége
v', akkor a relativisztikus sebességösszeadás
törvénye szerint az I-hez viszonyított sebességét a
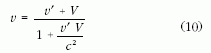
képlet határozza meg. Amikor a v' sebesség egy kis dv'-vel
megváltozik, akkor a v megfelelő megváltozása
(10) alapján a következő:

Gondolatmenetünkben a megfigyelt test a rakéta (vagy
az elektron) volt, amely a t pillanatban éppen nyugodott
I'-ben. Az I' V sebessége ekkor azonos a rakéta v sebességével,
és v' = 0. Ebben a speciális esetben (11)
valóban (6)-ra redukálódik.
2) A Lorentz-kontrakció képletének származtatása az
idődilatációból:
Haladjon egy vonat nyílegyenes pályán konstans V
sebességgel. A vonaton ülők a vonat hosszát a méterrúdjukkal megmérve
l0-nak találják. A vonat töltéshez viszonyított
hosszát a legegyszerűbben úgy lehet meghatározni,
hogy egy stopperrel valaki a töltésen állva megméri,
mennyi idő alatt halad el mellette a vonat. Ha erre 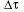 időt kap, akkor a vonat hossza
időt kap, akkor a vonat hossza 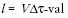 egyenlő. Az
időt itt azért célszerű
egyenlő. Az
időt itt azért célszerű 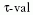 -val jelölni, mert ez annak a valakinek
a sajátideje, aki a mérést végzi.
A vonatban ülők mindebből annyit látnak, hogy V
sebességgel elsuhan mellettük egy ember stopperrel a
kezében, és
-val jelölni, mert ez annak a valakinek
a sajátideje, aki a mérést végzi.
A vonatban ülők mindebből annyit látnak, hogy V
sebességgel elsuhan mellettük egy ember stopperrel a
kezében, és 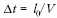 ideig tartózkodik a vonat mellett.
Ha a vonaton ülők között van olyan, aki ismeri a relativitáselméletet,
az azt is tudja, hogy a töltésen álló ember
stopperjén eközben
ideig tartózkodik a vonat mellett.
Ha a vonaton ülők között van olyan, aki ismeri a relativitáselméletet,
az azt is tudja, hogy a töltésen álló ember
stopperjén eközben
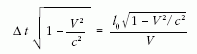
idő telt el. Ez az a 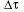 , amit a töltésen álló ember stopperje
mutat, ezért a töltéshez képest a vonat hossza ennek az
időnek a V-szerese:
, amit a töltésen álló ember stopperje
mutat, ezért a töltéshez képest a vonat hossza ennek az
időnek a V-szerese:
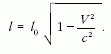
3) Miért éppen az
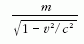
mennyiséget szokás mozgási tömegnek (vagy akár
látszólagos tömegnek) tekinteni? Azért, mert ez a kombináció
szerepel az impulzus (lendület) relativisztikus képletében:
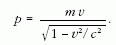
Ha azonban nem az impulzust, hanem a gyorsulást
vennénk alapul, akkor (8) szerint nem ezt, hanem az
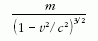
mennyiséget kellene mozgási (vagy látszólagos) tömegnek nevezni.
Ha a sebességnövekedéssel járó tömegnövekedés
ugyanolyan reális folyamat volna, mint a belső energia
növelésekor (például melegítéskor) bekövetkező tömegnövekedés,
amelyet a 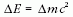 képlet határoz meg,
akkor nem választás kérdése lenne, hogy hogyan függ
egy test tömege a sebességétől. A szabad választás lehetősége
mutatja, hogy a mozgási tömeg csupán egy definíció,
amely - mint minden definíció - nem igaz vagy hamis,
hanem hasznos vagy haszontalan. Szerintem egyáltalán
nem hasznos, mert félrevezető.
képlet határoz meg,
akkor nem választás kérdése lenne, hogy hogyan függ
egy test tömege a sebességétől. A szabad választás lehetősége
mutatja, hogy a mozgási tömeg csupán egy definíció,
amely - mint minden definíció - nem igaz vagy hamis,
hanem hasznos vagy haszontalan. Szerintem egyáltalán
nem hasznos, mert félrevezető.
___________________________________________
1 Amikor a töltött részecske gyorsulása merőleges a sebességére, a 3/2
hatványkitevő 1/2-re módosul.
2 A (6) pontos levezetése a relativisztikus sebességösszeadás képletéből a
Függelékben megtalálható.
3 Ekvivalens-e egymással a tömeg és az energia? - Fizikai Szemle 53
(2003) 330
4 Special Relativity - Cambridge University Press, (1978) 114. oldal



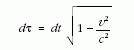
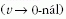 a newtoni mechanika a
relativitáselméletben is érvényes, ezért az űrhajóhoz képest
az (1) képlet igaz marad, csak időn természetesen az
űrhajóbeli
a newtoni mechanika a
relativitáselméletben is érvényes, ezért az űrhajóhoz képest
az (1) képlet igaz marad, csak időn természetesen az
űrhajóbeli 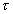 sajátidőt kell érteni:
sajátidőt kell érteni:

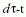 kifejezzük a földi időn keresztül:
kifejezzük a földi időn keresztül:
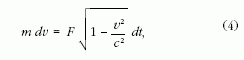
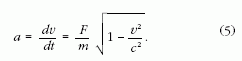
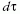 sajátidő-intervallumban a rakéta
I '-hez viszonyítva megtesz valamekkora - mondjuk dl0 -
utat. Ezalatt a rakéta sebessége I '-ben (vagyis "önmagához
képest") valamilyen dv'-vel nő meg. Mekkora dv
sebességnövekedésként fog ez megjelenni az I -beli megfigyelők
számára?
Abban az I inerciarendszerben, amelyből a rakéta
mozgását figyeljük, a dl0-nak a Lorentz-kontrakció szerint
sajátidő-intervallumban a rakéta
I '-hez viszonyítva megtesz valamekkora - mondjuk dl0 -
utat. Ezalatt a rakéta sebessége I '-ben (vagyis "önmagához
képest") valamilyen dv'-vel nő meg. Mekkora dv
sebességnövekedésként fog ez megjelenni az I -beli megfigyelők
számára?
Abban az I inerciarendszerben, amelyből a rakéta
mozgását figyeljük, a dl0-nak a Lorentz-kontrakció szerint
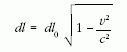
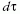 sajátidő-intervallumnak pedig
sajátidő-intervallumnak pedig
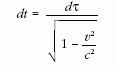
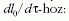 :
:
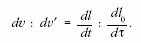
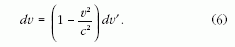

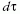 -t kifejezzük a földi megfigyelők által
észlelt dv-n és dt-n keresztül, az űrhajó gyorsulására az
-t kifejezzük a földi megfigyelők által
észlelt dv-n és dt-n keresztül, az űrhajó gyorsulására az
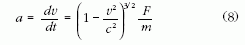
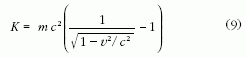
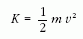
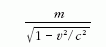
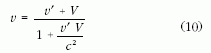

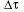 időt kap, akkor a vonat hossza
időt kap, akkor a vonat hossza 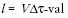 egyenlő. Az
időt itt azért célszerű
egyenlő. Az
időt itt azért célszerű 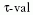 -val jelölni, mert ez annak a valakinek
a sajátideje, aki a mérést végzi.
A vonatban ülők mindebből annyit látnak, hogy V
sebességgel elsuhan mellettük egy ember stopperrel a
kezében, és
-val jelölni, mert ez annak a valakinek
a sajátideje, aki a mérést végzi.
A vonatban ülők mindebből annyit látnak, hogy V
sebességgel elsuhan mellettük egy ember stopperrel a
kezében, és 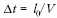 ideig tartózkodik a vonat mellett.
Ha a vonaton ülők között van olyan, aki ismeri a relativitáselméletet,
az azt is tudja, hogy a töltésen álló ember
stopperjén eközben
ideig tartózkodik a vonat mellett.
Ha a vonaton ülők között van olyan, aki ismeri a relativitáselméletet,
az azt is tudja, hogy a töltésen álló ember
stopperjén eközben
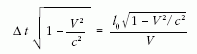
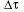 , amit a töltésen álló ember stopperje
mutat, ezért a töltéshez képest a vonat hossza ennek az
időnek a V-szerese:
, amit a töltésen álló ember stopperje
mutat, ezért a töltéshez képest a vonat hossza ennek az
időnek a V-szerese:
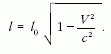
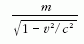
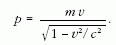
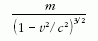
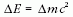 képlet határoz meg,
akkor nem választás kérdése lenne, hogy hogyan függ
egy test tömege a sebességétől. A szabad választás lehetősége
mutatja, hogy a mozgási tömeg csupán egy definíció,
amely - mint minden definíció - nem igaz vagy hamis,
hanem hasznos vagy haszontalan. Szerintem egyáltalán
nem hasznos, mert félrevezető.
képlet határoz meg,
akkor nem választás kérdése lenne, hogy hogyan függ
egy test tömege a sebességétől. A szabad választás lehetősége
mutatja, hogy a mozgási tömeg csupán egy definíció,
amely - mint minden definíció - nem igaz vagy hamis,
hanem hasznos vagy haszontalan. Szerintem egyáltalán
nem hasznos, mert félrevezető.