Fizikai Szemle 2006/3. 91.o.
OPTIKAI FREKVENCIAMETROLÓGIA, AVAGY MIRE JÓK A FREKVENCIAFÉSŰK?
Dombi Péter
MTA Szilárdtestfizikai és Optikai Kutatóintézet
Amikor a Nobel-díj kihirdetést követő órákban a kísérleti
munkájáért díjazott Theodor Hänsch német tudósnak
szegezték azt az újságírói kérdést, hogy miért is nyerhette
el ezt a kitüntetést, tömören és szerényen (és mellesleg
teljesen helytállóan is) úgy fogalmazott: "Nagyon pontos
méréseket végeztem ...."Ő John Hall amerikai fizikussal
megosztva kapta a díj felét a "lézeralapú precíziós spektroszkópiában"
elért eredményekért, az "optikai frekvenciafésű-
technikát is beleértve". Sokan esetleg már arról is
értesültek, hogy a frekvenciafésűk a femtoszekundumos
fényimpulzusokat kibocsátó lézerekre épülnek. Talán
nem árt a következőkben ezekre az összefüggésekre
pontosabban is rávilágítani annak kapcsán, hogy mik is
ezek a különleges nevű eszközök, nem megfeledkezve a
szép számban rendelkezésre álló érdekes alkalmazásokról és
magyar vonatkozásokról sem.
Femtoszekundumos lézerek
Mindenki látott már szivárványt vagy egy egyszerű üvegprizmán
való áthaladáskor spektrális komponenseire bomló
napfényt. A mindennapi lézerekről viszont legtöbbször a
monokromatikusság jut eszünkbe: a vonalkódleolvasók és
lézeres kulcstartók vörösétől kezdve a lézershow-k zöld
színéig sokféle tiszta színű lézerfénnyel találkozhatunk
mindennapjainkban is. Az utóbbi évek lézerfejlesztései viszont
lehetővé tették azt is, hogy bizonyos laboratóriumi
lézerek a Nap sugárzásához hasonló, közel fehér (vagyis
nagyon széles színskálát magában foglaló) sugárzást bocsássanak
ki. Ismert, hogy a különböző hullámhosszak különböző
fotonenergiáknak felelnek meg, tehát az ilyen lézerek
fényét úgy is tekinthetjük, mint amit nagyon nagy
(foton)energia-határozatlanság jellemez. Ezek után az sem
meglepő, hogy az ilyen lézerek nem folytonos, hanem nagyon
rövid ideig tartó, femtoszekundumos fényfelvillanásokra,
lézerimpulzusokra korlátozódó sugárzást adnak.
És ezen a ponton rögtön meg is kell emlékeznünk a
legutóbbi fizikai Nobel-díj egy magyar vonatkozásáról: az
ilyen ultragyors szilárdtestlézerek fejlesztésében egy
1994-es újítás is kulcsszerepet játszott: az MTA Szilárdtestfizikai
és Optikai Kutatóintézetében találták fel azokat az
- attól fogva világszerte, így a Nobel-díjas kutatásokhoz
igénybe vett lézerekben is felhasznált - speciális, fáziskorrigáló
(angolul chirped, s magyarul is néha "csörpölt")
tükröket, melyek azután lehetővé tették 10 fs-nál is rövidebb,
mindössze 1-2 optikai ciklusból1 álló lézerimpulzusok
előállítását. Az ilyen tükrökre épülő lézereket joggal
tekinthetjük tehát a Nobel-díjas mérésekhez felhasznált
műszerek előfutárainak.
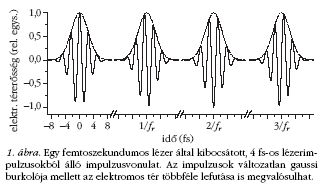
Frekvenciafésűk és ultrapontos mérések
Tovább árnyalja a helyzetet, hogy ezek a femtoszekundumos,
úgynevezett módusszinkronizált lézerek a fényimpulzusokat
periodikusan, több tucat MHz-es ismétlési
frekvenciával adják. Egy ilyen tipikus impulzusvonulatot
ábrázol az 1. ábra. Az elektromágneses tér ilyen lefutásának
frekvenciatartománybeli képe (vagyis a lézer spektruma)
egy frekvenciafésű: a széles burkoló alatt - amely
a vonulatbeli impulzusok extrém rövidsége miatt felölelheti
akár a teljes látható tartományt is - diszkrét, egyenközű
fésűfogak jelennek meg az impulzusok periodikus
ismétlődése miatt. A fésűfogak távolsága pedig fix és
éppen az fr ismétlési frekvenciával egyenlő. Így tehát
akár egy pontos frekvenciareferencia is keletkezhetne, ha
a struktúrát egyedül fr határozná meg, hiszen ez a paraméter
a lézerrezonátor hosszának függvénye, amit bevett
módszerekkel stabilizálni lehet. Van viszont még egy
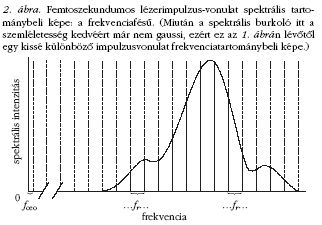
paraméter, mégpedig a teljes frekvenciafésű ofszetje
(2. ábra, fceo), amely nagyon érzékenyen reagálhat bármely,
lézerrezonátorbeli termikus vagy mechanikai fluktuációra,
vagy akár a femtoszekundumos lézert pumpáló másik,
általában folytonos lézer teljesítményzajára. Az ebből
származó fluktuáció, vagyis a frekvenciafésűnek a fix
spektrális burkoló alatt történő fel-alá vándorlása
(2. ábra) mind ez idáig nemigen zavarta az ilyen lézerek
felhasználóit, hiszen egy ilyen zaj mellett a lézerimpulzusok
időtartománybeli képe meglehetősen változatlan
marad (pontosabban szólva az ismétlési frekvenciát és az
impulzusok időbeli burkolójának lefutását ez nem befolyásolja).
Hiperpontos spektroszkópiára, frekvenciamérésre
viszont nyilvánvalóan alkalmatlan egy ilyen zajos,
fel-alá mozgó frekvenciafésű. Az eddigieket tehát matematikai
alakba öntve: az n-edik fésűfog pozícióját az
fn = nfr + fceo
egyenlettel lehet leírni, ahol n egy nagy természetes
szám, és a fentiek alapján fceo jelentős zajjal terhelt
is lehet. Az fceo ofszet stabilizálását viszont megnehezíti az
a tény, hogy nem lehet közvetlenül mérni: a 0 frekvencia
közelében nincs jel (2. ábra).
A Nobel-díjasokat viszont nem tántorította vissza ez a
tény, és nem adták fel azt, hogy valaha egy ilyen, spektrális
tartománybeli vonalzó segítségével frekvenciát, hullámhosszat
mérhessenek. A lézertechnológia fejlődése azonban
csak 4-5 éve tette lehetővé azt a lépést, ami - az erre
épülő alkalmazásokkal együtt - mostanra már Nobel-díjat
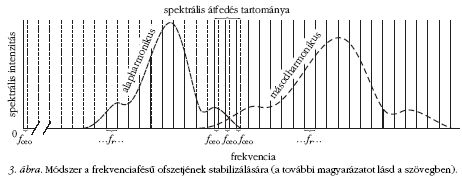
is ért. Az alapötlet a következő volt: az optikában már a lézerek
félévszázada történt megjelenése óta ismert a frekvenciakétszerezés:
megfelelő nemlineáris kristályokban
például800 nm-es vörös fényből400 nm-es kék fényt lehet
előállítani. Ha a frekvenciafésűnkön hajtjuk ezt végre, akkor
a spektrális tartományban egy másodharmonikus frekvenciafésű-
másolat jelenik meg (3. ábra), 2(nfr + fceo)-nál
elhelyezkedő fésűfogakkal. Ha ezen felül az eredeti
fésű oktáv szélességű, akkor a másodharmonikus fésű
alacsony frekvenciás vége átfed az eredeti nagyfrekvenciás
végével, és az átfedési tartományban a két fésűből
származó fogak közti lebegési frekvencia éppen az eredeti
fésű ofszetjével lesz egyenlő, mint azt egyszerűen
ellenőrizni is tudjuk a
2(nfr + fceo) - (2nfr + fceo) =
fceo
egyenletből. Miután ez a frekvencia 0 és fr között van,
ezért ez elektronikus eszközökkel feldolgozható, és a
lézeroszcillátorba vissza lehet csatolni egy olyan hibajelet,
mellyel az oszcillátor ezen utolsó, kontrollálatlan
paramétere is szabályozhatóvá válik.
Ha pedig ilyen módon adott
már egy fix frekvenciafésű, akkor
ultrapontos méréseket sem
nehéz már végezni: csak annyit
kellene tudni, hogy mely két fésűfog
között van a mérendő
spektrumvonal (ez a körülbelüli
érték klasszikus spektroszkópiai
módszerekkel könnyedén meghatározható),
majd a két szomszédos
fésűfoghoz viszonyított
lebegési frekvencia (amely néhány
MHz-es, a rádiófrekvenciás tartományba eső, vagyis
nagyon pontosan mérhető jel) meghatározásával már
igen nagy pontossággal is meg lehet állapítani a mérendő
spektrumvonal helyét. Egy ilyen fix, referenciavonalakat
adó fényforrást talán indokoltabb is lenne (a bevettebb) a
frekvenciafésű helyett inkább frekvenciavonalzónak nevezni:
ahogy egy hagyományos vonalzóval pontos távolságok
mérhetők, úgy ezzel az eszközzel tiszta színek,
vagyis: hullámhosszak, frekvenciák. Ezen az alapon azután
el is végeztek néhány nagyon pontos mérést, egy
csapdázott higanyion egy optikai elektronátmenetének
frekvenciáját például 1064721609899143 (±10) Hz-nek
mérték, vagyis a bizonytalanság mindössze 10-14-es mértékű.
Persze optikai spektrumvonalak egzakt helyét 4-5
évvel ezelőttig is meg tudták állapítani, csakhogy ennél
több nagyságrenddel pontatlanabbul és több tucatszor
drágább eszközparkkal. A Nobel-díjjal jutalmazott munka
azonban a világszerte létező 4-5 nagy, nemzeti szabványügyi
laboratórium után egyetemi kutatócsoportok számára
is lehetővé tette az optikai tartománybeli ultrapontos
frekvenciamérést.

A frekvenciafésűk további alkalmazásai
a kozmológiában és az időmérésben
A módszert felhasználva megtörtént az első jelentős alkalmazás
is, amelynek során Theodor Hänsch csoportja
azt vizsgálta meg, hogy valóban állandók-e a fizikai állandók.
Már eddig is létezett ugyanis pár olyan egzotikus
kozmológiai elmélet, amely feltételezte, hogy a konstansok
lassan ugyan, de időben változhatnak - ezeket a teóriákat
kellett hát valamiképpen tesztelni. Vannak olyan
spektrumvonalak (pl. a hidrogénspektroszkópiában),
amelyek egyszerű kapcsolatban állnak fizikai állandókkal
(pl. az elektron töltésével és a Planck-állandóval). A
spektrumvonal helyének precíz meghatározásával tehát
tulajdonképpen ezek a konstansok is extrém pontosan
mérhetők. Nincs is más teendő, mint a frekvenciafésűk
segítségével néhány évenként kimérni ezen vonalak helyét.
Aggodalomra azonban mindeddig semmi ok: a
négyéves időközzel megismételt méréspárban úgy találták,
hogy az észlelt elmozdulás még a nagyon alacsony
mérési hibahatáron is belül van, tehát a konstansok jelenleg
állandóaknak tűnnek ....
Persze azon túl, hogy egzotikus elméletekhez szolgáltattak
adalékot, a közeljövőben sokkal hétköznapibb
alkalmazásokhoz is hozzájárulhatnak az ilyen lézerek.
Egy ilyen tipikus terület pedig az időmérés. Minden óra
két részből áll ugyanis: egyrészt egy pontosan ismert
frekvenciával periodikusan ismétlődő eseményből (pl. a
napóránál a Föld tengely körüli forgásából, a kvarcóránál
egy kvarckristály oszcillációiból), másrészt egy
számlálóból, amely ezeket a periodikusan bekövetkező
eseményeket számlálja. Belátható, hogy minél nagyobb
frekvenciával ismétlődő eseményeket választunk az óra
alapjául, annál pontosabban tudunk időt mérni: egy
cézium-atomóra (ahol egy mikrohullámú atomi átmenet
frekvenciáját számlálják) tízmilliárdszor pontosabbá
tehető, mint például egy ingaóra. A látható fény frekvenciája
azonban még a már ötven éve a csúcstechnológiát
jelentő atomórákban felhasznált frekvenciáknál is
legalább negyvenezerszer nagyobb, ezen az alapon tehát
több nagyságrenddel pontosabb óra is építhető, ráadásul
lényegesen kompaktabb eszközökkel. Ez a jövőben
akár az atomórákat is túlszárnyaló, optikai tartománybeli
frekvenciára épülő másodperc-definíciót tehet
lehetővé, s potenciális gyakorlati alkalmazásokat sem
nehéz találni: például ezen az alapon a globális helymeghatározást
(GPS-t) is tovább lehetne fejleszteni,
ahol a térbeli pontosság növelése éppen az időmérés
pontosabbá tételével érhető el.
A frekvenciafésűkhöz használt lézertípus azonban
más, érdekes alapkutatási kérdésekben is hozott már újat:
a már jól ismertnek hitt és tudománytörténetileg is jelentős
fémfelületi fotoelektron-emisszió egy új arcát sikerült
nemrég kísérletileg is kimutatnunk a segítségükkel (részben
szintén Theodor Hänsch csoportjával való együttműködésben).
Az utóbbi években pedig az attoszekundumos
(1 as = 10-18 s) alkalmazások is egyre nagyobb publicitást
kaptak: Farkas Gyozo (MTA Szilárdtestfizikai és
Optikai Kutatóintézet) 1991-es javaslata alapján néhány
éve sikerült 250 attoszekundumos röntgenimpulzusokat
is előállítani Krausz Ferenc akkor még bécsi csoportjában
(jelenleg: Kvantumoptikai Max Planck Intézet, Garching),
aki ezen eredményei kapcsán név szerint is szerepel a
Nobel-díjról kiadott hivatalos anyagban. Attoszekundumos
impulzusokkal, melyek jelenleg az ember
által kontrollálhatóan előállítható legrövidebb elemi események,
szintén nagyon pontos méréseket lehet végezni,
bár kicsit másképp, mint a frekvenciafésűkkel: a természetben
lejátszódó leggyorsabb folyamatok időbeli lefutásáról
nyerhetünk információt. Ezt a módszert már fel is
használták atomok belső elektronhéjain lezajló atomfizikai
folyamatok vizsgálatához. A közeljövőben pedig ilyen
kísérletekkel talán választ kaphatunk arra a kérdésre is,
hogy miként lehetne elég nagy fényerejű, a lézerekhez
hasonló, viszont a röntgentartományban működő fényforrásokat
létrehozni, melyekkel az orvosi/biológiai képalkotási
eljárásokat lehetne forradalmasítani és a vizsgált
személyek és minták sugárterhelését lényegesen csökkenteni.
Az attoszekundumos alkalmazásokról azonban a
Fizikai Szemle 2002. évi 1. számában már megjelent egy
kimerítő bevezetés.
A femtoszekundumos lézerek és az azokra épülő kísérletek
tehát izgalmasabbnak tűnnek, mint valaha, és
biztos vagyok abban, hogy a következő években ilyen
fényforrásokkal elért újabb jelentős eredményeknek lehetünk
majd szemtanúi.
Irodalom
TH. UDEM, R. HOLZWARTH, T.W. HÄNSCH: Optical frequency metrology -
Nature 416 (2002) 233
M. FISCHER ET AL.: New limits on the drift of fundamental constants
from laboratory measurements - Phys. Rev. Lett. 92 (2004) 230802
A. APOLONSKI, P. DOMBI ET AL.: Observation of light-phase-sensitive photoemission
from a metal - Phys. Rev. Lett. 92 (2004) 073902
KRAUSZ FERENC: Atomok és elektronok mozgásban - Fizikai Szemle 52
(2002) 12
