Fizikai Szemle 2006/03. 96.o.
ERATOSZTENÉSZ-MÉRÉS
- egy 2200 éves mérés megismétlése
Nyerges Gyula
Zsigmondy Vilmos Gimn. és Informatikai Szki., Dorog
Történeti háttér
Kr. e. 200 táján az alexandriai Eratosztenész Sziénében
(ma Asszuán) járva különös jelenségre lett figyelmes: egy
mély kútba tekintve meglátta a delelő nap fényét a vízben
tükröződni. Ilyet otthon még soha nem látott, elgondolkodott
hát, s felismerte a lehetőséget.
A kút fenekén megcsillanó napfény azt jelenti, hogy a
fényes égitest a zenitben (vagyis éppen az észlelő feje
fölött) jár. Alexandriában azért nem delel a Nap a zenitben,
mert jóval északabbra (mai terminológiával a Ráktérítőtől
északra) fekszik. A Föld gömb alakja ekkor már
ismert volt, a holdfogyatkozások alkalmával ugyanis
midig körív alakú árnyékot vet a Holdra. Az átmérő tekintetében
viszont csupán becslések születtek, igen nagy
szórást mutatva. Ha sikerül azonos időpontban két különböző
földrajzi helyen megmérni a Nap delelési magasságát,
a szögek különbségéből és a mérési pontok távolságából
a Föld kerülete meghatározható.
Az egyik mérési pont célszerűen Sziéné lett, hiszen itt
már nem is volt szükség mérésre. A két mérés egyidejű
megvalósítására a nagy távolság miatt nem volt mód, azt
viszont tudni lehetett, hogy a Nap évről évre rendre
ugyanazt az utat járja be az égbolton, így pontosan egy
évvel később bízvást várhatjuk, hogy a kút fölött ismét a
zenitben delel majd. Ekkor kell hát a második mérést
elvégezni!
A mérésre tehát a következő évben került sor Alexandriában.
Egy oszlop magasságát és az árnyék hosszát
kellett megmérni, épp délben (1. ábra). Időmérésre pontosabb
alkalmatosság híján napórát használhatunk, de ha
ez sem áll rendelkezésünkre, elegendő a nap közben
változó hosszúságú árnyék minimális hosszát megállapítani.

A mért adatok segítségével a keresett szög (a Nap zenittávolsága)
megszerkeszthető. (Számításra nincs mód,
hiszen a szögfüggvényeket majd csak 1000 év múlva fogják
kitalálni, tangenstáblázatot pedig 1600 év múlva készít
Regiomontanus - talán épp Esztergomban.) A kapott
szöget többször lemásolva Eratosztenész megállapította,
hogy az a teljes kör 1/50 része. A Föld kerülete tehát a
két város távolságának éppen 50-szerese. A távolságot
akkoriban sztadionban mérték, a naponta 100 sztadionnyi
utat megtevő karaván 50 nap alatt ért Alexandriából
Sziénébe, a távolság tehát 5000 sztadion, a Föld kerületére
így 25000 sztadion adódott. (Az ógörög mértékegységek
átváltását SI-re jelentős mértékben megnehezíti, hogy
minden városállamnak különböző méretű volt a stadionja,
aminek a kerülete távolságegységként szolgált. A
25000 sztadion 36 000 és 46000 km közötti távolság, legvalószínűbb
értéke 39 375 km.)
A felhívás
A norvég GLOBE Europe a Fizika Éve alkalmából nemzetközi
együttműködésre hívta fel a világ iskoláit. Az
akció keretében május 25-én a Föld több tucat iskolájában
mérték meg a delelő nap zenittávolságát. A kapott
mérési adatok birtokában és a mérési pontok földrajzi
helyének ismeretében Eratosztenész módszerét követve
megállapítható a Föld mérete.

A felhívás megismerése után elhatároztam, hogy megpróbálom
a hazai részvételt megszervezni. Az akció
angol nyelvű honlapját: (
http://www.naturfagsenteret.no/fysikk/eratosthenes) Kiss László (Sydney) fordította
magyarra. A magyar változat (2. ábra) a Fizika Éve magyar
oldalain nyert elhelyezést
(http://wyp.csillagaszat.hu/files/eratosthenes/how.html).
A méréssel kapcsolatban több kétely is napvilágot
látott. Eratosztenész mérési pontjai, Alexandria és Sziéné
nagyjából azonos meridiánon fekszenek. Megengedhető-e
két olyan iskola adatainak összehasonlítása, amelyeknek
eltér a földrajzi hosszúsága? Ez a probléma áthidalható, ha
nem a két iskola távolságát, csupán a két ponthoz tartozó
szélességi kör távolságát használjuk fel, cserében olyanok
is részt vehetnek a mérésben, akik nem találnak partnert
saját délkörükön. A másik probléma a távolságok számításával
kapcsolatban merült fel. Ha a földrajzi koordináták
felhasználásával határozzuk meg a szélességi körök távolságát,
a számításhoz ismerni kell a Föld kerületét,
vagyis pontosan azt a mennyiséget, amit a kísérlettel kívánunk
meghatározni. Ennek feloldására azt javasoltuk,
hogy a távolságot ne számítással, hanem a térképen való
méréssel, az ottani lépték felhasználásával határozzák
meg, hiszen a térképek alapvetően távolságmérési adatok
alapján készültek (legalábbis Eratosztenész idejében).

A mérés
A mérést 2 időpontra hirdették meg.
Az első május 25. (ill. a 23-27. közötti időszak, hogy
azok se maradjanak ki a mérésből, akiknél 25-én éppen
borult az ég). 23-án "főpróbát" tartottunk az iskola kosárlabda-
pályáján. Közép-európai idő szerint 11 és 13 óra
között 3 módszerrel végeztünk méréseket:
- Mérőpárok Bunsen-állvány árnyékát rajzolták 5 perces
idoközzel (3. ábra). Az állvány magasságának és az
árnyék hosszának mérésével állapították meg a keresett
szöget.
- Mikola-cső állványát alakítottuk át oly módon, hogy
alkalmas legyen a mérésre. A szertárban talált törött Mikola-
csövet eltávolítottuk a tartójából. A megmaradt falécet
a Nap irányába forgatva a mögé helyezett papírlapon
minimális az árnyék mérete. Ekkor kell a hozzá tartozó
szögmérőről leolvasni a Nap horizont feletti magasságát
(4. ábra)
- Táblai szögmérőt egészítettünk ki függőónnal. A
"célzás" itt is árnyék-vizsgálattal történt.
A mérés végeztével még a helyszínen kiértékeltük és
összehasonlítottuk a mérési eredményeket.
25-én elérkezett az "igazi" mérés időpontja. A két nappal
korábbi tapasztalatokon okulva pontosítottuk módszereinket,
vízmértékkel ellenőriztük a Bunsen-állványok
függőlegességét, GPS-vevővel pontosítottuk a mérési
hely koordinátáit. Kipróbáltunk egy negyedik mérési
módszert is, melynek ötlete a főpróba során fogalmazódott
meg bennem:
- A módszer tulajdonképpen az elsővel megegyező,
csupán az eleve rendelkezésre álló kosárlabdapalánkot
használtuk árnyékvetőnek.
A mérés kezdetekor némi aggodalomra adott okot a
folyamatosan vonuló felhőzet, de hamarosan kitisztult,
és a későbbiekben csupán 10 percre zavart meg minket
egy kisebb felhő. Az egyhangú munkát színesítendő
meghívtam Tóth Tibor barátomat, aki saját csillagászati
távcsövével tartott Nap-bemutatást a mérés résztvevőinek,
valamint a szünetekben a tanulóifjúságnak és az
iskola érdeklődő dolgozóinak (5. ábra ). Az igazgatótól
a konyhásig mindenki nagy örömmel fogadta e lehetőséget,
és lelkesen hallgatták a napfoltokról szóló rögtönzött
előadást.
Eredmények
A mért eredmények jó közelítéssel azonos értéket mutattak.
A Nap zenittávolságára: 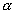 ?= 26°30'±30' adódott.
Az adatok szórását véleményünk szerint az árnyékvető
rudak vastagsága, valamint a napkorong kiterjedése
(nem pontszerű, hanem fél fok átmérőjű fényforrás)
okozta.
?= 26°30'±30' adódott.
Az adatok szórását véleményünk szerint az árnyékvető
rudak vastagsága, valamint a napkorong kiterjedése
(nem pontszerű, hanem fél fok átmérőjű fényforrás)
okozta.

A következő napokban izgalommal vártuk az interneten
megjelenő mérési eredményeket. A lassan gyűlő
adatok közül a finn Palokan Koulu adatait használtuk
fel. Az adatok összevetéséből 40 136 km jött ki a Föld
kerületére.

Pályázat
Az akció népszerűsítése céljából pályázatot hirdettünk a
mérésben részt vevő iskolák számára. Pályázni a méréssel
kapcsolatos elektronikus publikációval (számítógépes
prezentáció vagy videoklip) lehet. A pályaműveket október
közepéig kellett beküldeni.

A díjazottak természettudományos könyveket, informatikai
eszközöket, és egy csillagászati távcsövet nyertek.
A nyertesek listája megtekinthető a
http://antares.dorogi-gimn.sulinet.hu/eratosthenes/eredmeny.html
honlapon (6. ábra).
A mérés jelentősége
Az akcióban részt vevő tanulók egy valódi kísérlet részeseivé
váltak. Megismerhették a mérés előkészítésével, lebonyolításával,
kiértékelésével kapcsolatos munkát, a közben
felmerülő esetleges problémákat. Ráadásul ez nem egy
elszigetelt, hanem nemzetközi "projekt", ami további érdekességgel
és újabb tapasztalatokkal járt. A mérés alapvetően
fizikai jellegű, szöget kellett mérni, közvetlenül, vagy
távolságmérésre visszavezetve. Az adatok kiértékeléséhez
matematikai módszerekre van szükség, de ez a fizikai feladatoknál
magától értetődő dolog. Az eredmények értelmezéséhez
és feldolgozásához viszont csillagászati és földrajzi
ismeretek szükségesek. Mivel egy 2200 éves mérés
megismétléséről van szó, nem árt felfrissíteni történelmi
ismereteinket, hogy a megfelelő korba helyezhessük a
kísérletet. A nemzetközi együttműködés lebonyolításához
az informatikában való jártasság és idegennyelv-ismeret
szükséges. Az általunk kiírt pályázatban való részvételhez
mindezek felett a vizuális kultúra alapismereteinek alkalmazása
is nélkülözhetetlen. Bátran állíthatjuk tehát, hogy
az Eratosztenész-mérés valóban interdiszciplináris kaland
volt valamennyi résztvevő tanuló (és pedagógus) számára.

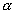 ?= 26°30'±30' adódott.
Az adatok szórását véleményünk szerint az árnyékvető
rudak vastagsága, valamint a napkorong kiterjedése
(nem pontszerű, hanem fél fok átmérőjű fényforrás)
okozta.
A következő napokban izgalommal vártuk az interneten
megjelenő mérési eredményeket. A lassan gyűlő
adatok közül a finn Palokan Koulu adatait használtuk
fel. Az adatok összevetéséből 40 136 km jött ki a Föld
kerületére.
?= 26°30'±30' adódott.
Az adatok szórását véleményünk szerint az árnyékvető
rudak vastagsága, valamint a napkorong kiterjedése
(nem pontszerű, hanem fél fok átmérőjű fényforrás)
okozta.
A következő napokban izgalommal vártuk az interneten
megjelenő mérési eredményeket. A lassan gyűlő
adatok közül a finn Palokan Koulu adatait használtuk
fel. Az adatok összevetéséből 40 136 km jött ki a Föld
kerületére.