Fizikai Szemle honlap |
Tartalomjegyzék |
Vinkó József
SZTE Optikai és Kvantumelektronikai Tanszék
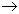 56Co
56Co
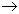 56Fe radioaktív bomlás
viszont még évekig képes belülről fűteni a felhőt, ezért
lényegében ennek a folyamatnak köszönhetjük, hogy a
SN-kat hosszú ideig tanulmányozhatjuk. A fénygörbe
leszálló ágának konstans meredeksége pontosan a 56Co
56Fe radioaktív bomlás
viszont még évekig képes belülről fűteni a felhőt, ezért
lényegében ennek a folyamatnak köszönhetjük, hogy a
SN-kat hosszú ideig tanulmányozhatjuk. A fénygörbe
leszálló ágának konstans meredeksége pontosan a 56Co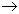 56Fe bomlás időállandójának felel meg.
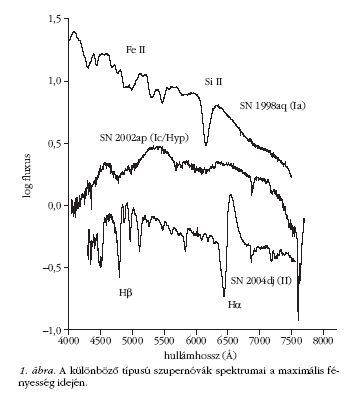
A fénygörbék hasonlósága ellenére a SN-k spektruma
igen különböző lehet. Az I-es típusú SN-k spektrumában
nincs hidrogénre utaló vonal, ezzel szemben a II-es típusú
SN-k színképében a hidrogén vonalai dominálnak (1.
ábra). Az I-es típus további altípusokra oszlik. Az Ia
típus jellegzetessége az egyszeresen ionizált szilícium (Si
II) vonalainak megjelenése. Az Ib típusú SN spektrumában
a He vonalai erősek, míg az Ic típusba tartozók
spektrumában sem Si, sem He nincs, ezeknél főként ionizált
vas (Fe II és Fe III) figyelhető meg.
A spektrumok időbeli fejlődése hasonló a különböző
típusoknál. A maximális fényesség környékén kék kontinuum
figyelhető meg, ami a ledobódott gázfelhő magas
hőmérsékletére utal. A kontinuumra úgynevezett
P Cygni-profilú erős vonalak rakódnak rá, melyek egy
széles emissziós komponensből és egy ehhez képest
kékeltolódott abszorpciós komponensből állnak (mint
például az SN 2004dj H? vonala az 1. ábrán). Ilyen vonalprofilok
nagy sebességgel táguló atmoszférában jönnek
létre. A vonalprofilt leszámítva a színkép hasonlít a
normális csillagok színképére, ezért ezt a szakaszt fotoszferikus
fázisnak nevezzük. A későbbiekben a kontinuum
gyengül, ellaposodik, majd szinte teljesen eltűnik.
Az emissziós vonalak megerősödnek, és megjelennek
tiltott átmenetek vonalai is (2. ábra ). Ekkor a színkép
már egy átlátszó gázköd spektrumára emlékeztet,
ez a nebuláris fázis.
A legtöbb SN nagy tömegű csillagok összeomlásából
jön létre (3. ábra, jobb oldal). Amikor egy 8 naptömegnél
(
56Fe bomlás időállandójának felel meg.
A fénygörbék hasonlósága ellenére a SN-k spektruma
igen különböző lehet. Az I-es típusú SN-k spektrumában
nincs hidrogénre utaló vonal, ezzel szemben a II-es típusú
SN-k színképében a hidrogén vonalai dominálnak (1.
ábra). Az I-es típus további altípusokra oszlik. Az Ia
típus jellegzetessége az egyszeresen ionizált szilícium (Si
II) vonalainak megjelenése. Az Ib típusú SN spektrumában
a He vonalai erősek, míg az Ic típusba tartozók
spektrumában sem Si, sem He nincs, ezeknél főként ionizált
vas (Fe II és Fe III) figyelhető meg.
A spektrumok időbeli fejlődése hasonló a különböző
típusoknál. A maximális fényesség környékén kék kontinuum
figyelhető meg, ami a ledobódott gázfelhő magas
hőmérsékletére utal. A kontinuumra úgynevezett
P Cygni-profilú erős vonalak rakódnak rá, melyek egy
széles emissziós komponensből és egy ehhez képest
kékeltolódott abszorpciós komponensből állnak (mint
például az SN 2004dj H? vonala az 1. ábrán). Ilyen vonalprofilok
nagy sebességgel táguló atmoszférában jönnek
létre. A vonalprofilt leszámítva a színkép hasonlít a
normális csillagok színképére, ezért ezt a szakaszt fotoszferikus
fázisnak nevezzük. A későbbiekben a kontinuum
gyengül, ellaposodik, majd szinte teljesen eltűnik.
Az emissziós vonalak megerősödnek, és megjelennek
tiltott átmenetek vonalai is (2. ábra ). Ekkor a színkép
már egy átlátszó gázköd spektrumára emlékeztet,
ez a nebuláris fázis.
A legtöbb SN nagy tömegű csillagok összeomlásából
jön létre (3. ábra, jobb oldal). Amikor egy 8 naptömegnél
(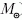 ) nagyobb tömegű csillag magjában a fúziós energiatermelés
végén inaktív vasmag jön létre, a mag lassan
elkezd összehúzódni, amit még az elfajult elektrongáz
nyomása sem képes megállítani. Egy kritikus sűrűség elérésekor
beindul a
) nagyobb tömegű csillag magjában a fúziós energiatermelés
végén inaktív vasmag jön létre, a mag lassan
elkezd összehúzódni, amit még az elfajult elektrongáz
nyomása sem képes megállítani. Egy kritikus sűrűség elérésekor
beindul a
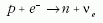
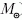 ). Ekkor a fehér törpe összeroppan,
belsejében beindul a szén és az oxigén fúziója. Mivel az
elfajult állapotú anyag nyomása nem függ a hőmérséklettől,
a fúziós energiatermelés teljes egészében a fúziós ráta
növelésére fordítódik, ezért a reakció a fehér törpe teljes
nukleáris felrobbanásához vezet. Ezért az Ia típusú SN-kat
szokás termonukleáris SN-knak is nevezni. Mivel a
robbanó objektum mindig nagyjából ugyanolyan tömegű
és összetételű, a robbanás megfigyelt jellemzői is hasonlóak
lesznek. A többi SN-robbanásban a felrobbanó csillag
tömege széles határok között változhat, ezért azok
sokkal heterogénebb képet mutatnak.
Ia típusú SN-k mindenféle galaxisban előfordulnak,
ezzel szemben a többi SN kizárólag spirálgalaxisokban,
azokon belül is főleg spirálkarokban, csillagképző területeken
figyelhető meg. Ez teljesen összhangban van a keletkezésükről
fentebb vázolt modellekkel, hiszen a nagy
tömegű csillagok főként a spirálkarokban születnek.
Nagy átlagban egy galaxisban 50-100 évente tűnik fel
egy SN, de vannak ennél négyszer-ötször nagyobb SN-gyakoriságot
mutató galaxisok is. A Tejútrendszerben
utoljára 1604-ben, Kepler korában figyelhettek meg SN-t.
Természetesen az eltelt 400 évben több SN is felrobbanhatott
a Tejútrendszerben, de azokat a galaxisunk nagy
részét a földi észlelők elől elfedő csillagközi por miatt
nem vettük észre.
). Ekkor a fehér törpe összeroppan,
belsejében beindul a szén és az oxigén fúziója. Mivel az
elfajult állapotú anyag nyomása nem függ a hőmérséklettől,
a fúziós energiatermelés teljes egészében a fúziós ráta
növelésére fordítódik, ezért a reakció a fehér törpe teljes
nukleáris felrobbanásához vezet. Ezért az Ia típusú SN-kat
szokás termonukleáris SN-knak is nevezni. Mivel a
robbanó objektum mindig nagyjából ugyanolyan tömegű
és összetételű, a robbanás megfigyelt jellemzői is hasonlóak
lesznek. A többi SN-robbanásban a felrobbanó csillag
tömege széles határok között változhat, ezért azok
sokkal heterogénebb képet mutatnak.
Ia típusú SN-k mindenféle galaxisban előfordulnak,
ezzel szemben a többi SN kizárólag spirálgalaxisokban,
azokon belül is főleg spirálkarokban, csillagképző területeken
figyelhető meg. Ez teljesen összhangban van a keletkezésükről
fentebb vázolt modellekkel, hiszen a nagy
tömegű csillagok főként a spirálkarokban születnek.
Nagy átlagban egy galaxisban 50-100 évente tűnik fel
egy SN, de vannak ennél négyszer-ötször nagyobb SN-gyakoriságot
mutató galaxisok is. A Tejútrendszerben
utoljára 1604-ben, Kepler korában figyelhettek meg SN-t.
Természetesen az eltelt 400 évben több SN is felrobbanhatott
a Tejútrendszerben, de azokat a galaxisunk nagy
részét a földi észlelők elől elfedő csillagközi por miatt
nem vettük észre.
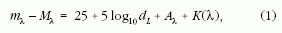
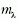 a mért,
a mért,
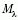 az abszolút magnitúdó, dL az úgyne-
vezett luminozitási távolság (megaparszekben),
az abszolút magnitúdó, dL az úgyne-
vezett luminozitási távolság (megaparszekben), 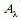 a
csillagközi por miatti fényességcsökkenés (magnitúdóban),
a
csillagközi por miatti fényességcsökkenés (magnitúdóban),
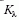 pedig az úgynevezett K-korrekció. Az utolsó tag
azért lép fel, mert a távoli SN-k az Univerzum tágulása
miatt vöröseltolódást szenvednek, megváltozik a megfigyelt
spektrális energiaeloszlásuk, ezáltal egy adott szűrővel
mért fényességük különbözni fog attól, mint amit
nulla vöröseltolódásnál mérnénk.
(1) értelmében a luminozitási távolság kiszámításához
az összes többi tényezőt ismernünk kell.
pedig az úgynevezett K-korrekció. Az utolsó tag
azért lép fel, mert a távoli SN-k az Univerzum tágulása
miatt vöröseltolódást szenvednek, megváltozik a megfigyelt
spektrális energiaeloszlásuk, ezáltal egy adott szűrővel
mért fényességük különbözni fog attól, mint amit
nulla vöröseltolódásnál mérnénk.
(1) értelmében a luminozitási távolság kiszámításához
az összes többi tényezőt ismernünk kell. 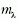 a SN fotometriájából
elvileg meghatározható, erre jól bevált eljárások
léteznek a csillagászatban.
a SN fotometriájából
elvileg meghatározható, erre jól bevált eljárások
léteznek a csillagászatban. 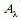 szintén mérhető, bár
jóval bizonytalanabbul. Erre főként a SN kék (B) és zöld
(V) szűrővel mért magnitúdójának különbségét, a B-V
színindexet használják. A megfigyelések szerint az Ia
SN-k B-V görbéje a maximum után 1-3 hónappal nagyon
hasonló lefutású (a SN-k spektrumának homogenitása
miatt). Az ettől való eltérést a csillagközi por vörösítő
hatása okozza, amelyből a standard vörösödési törvény
segítségével
szintén mérhető, bár
jóval bizonytalanabbul. Erre főként a SN kék (B) és zöld
(V) szűrővel mért magnitúdójának különbségét, a B-V
színindexet használják. A megfigyelések szerint az Ia
SN-k B-V görbéje a maximum után 1-3 hónappal nagyon
hasonló lefutású (a SN-k spektrumának homogenitása
miatt). Az ettől való eltérést a csillagközi por vörösítő
hatása okozza, amelyből a standard vörösödési törvény
segítségével 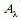 kiszámítható a vizsgált hullámhossztartományon.
kiszámítható a vizsgált hullámhossztartományon.
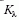 becsléséhez lokális (tehát gyakorlatilag 0
vöröseltolódású) SN-k spektrumait használják, melyeket
az adott vöröseltolódáshoz transzformálnak, ebből azután
kiszámítható a korrekció mértéke. Ehhez szintén azt
használják ki, hogy a különböző Ia SN-k spektruma nagyon
hasonlít egymáshoz mind a fotoszferikus, mind a
nebuláris fázisban. Ebben a feltevésben implicite az is
benne van, hogy a nagy vöröseltolódású (tehát nemcsak
térben, hanem időben is távoli) Ia SN-k ugyanolyan fizikai
tulajdonságúak, mint lokális megfelelőik, vagyis ezeknek
az objektumoknak nincs "kozmológiai" evolúciója.
A "standard gyertya" hipotézis értelmében
becsléséhez lokális (tehát gyakorlatilag 0
vöröseltolódású) SN-k spektrumait használják, melyeket
az adott vöröseltolódáshoz transzformálnak, ebből azután
kiszámítható a korrekció mértéke. Ehhez szintén azt
használják ki, hogy a különböző Ia SN-k spektruma nagyon
hasonlít egymáshoz mind a fotoszferikus, mind a
nebuláris fázisban. Ebben a feltevésben implicite az is
benne van, hogy a nagy vöröseltolódású (tehát nemcsak
térben, hanem időben is távoli) Ia SN-k ugyanolyan fizikai
tulajdonságúak, mint lokális megfelelőik, vagyis ezeknek
az objektumoknak nincs "kozmológiai" evolúciója.
A "standard gyertya" hipotézis értelmében 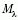 elvileg
minden Ia SN-ra ugyanaz, és ez az érték kalibrálható. A
90-es évek közepére azonban nyilvánvalóvá vált, hogy az
erre irányuló törekvések kudarca amiatt van, mert a
"standard gyertya" hipotézis nem igaz. Az évtized elején
indult szisztematikus SN-kereső programok első eredményeiből
kiderült, hogy az Ia SN-k maximális abszolút fényessége
legalább 1-1,5 magnitúdós szórást mutat, ami
nem a mérési hibából származik. Szerencsére az is bebizonyosodott,
hogy a maximális fényesség korrelál a SN-k
egyéb mérhető paramétereivel. Az egyik ilyen paraméter
a B-szűrős fénygörbe időbeli lefutása. Erre kétféle kalibrációs
eljárást is kidolgoztak. Az egyik a nyújtási módszer,
amely szerint az időtengely skálázásával (
elvileg
minden Ia SN-ra ugyanaz, és ez az érték kalibrálható. A
90-es évek közepére azonban nyilvánvalóvá vált, hogy az
erre irányuló törekvések kudarca amiatt van, mert a
"standard gyertya" hipotézis nem igaz. Az évtized elején
indult szisztematikus SN-kereső programok első eredményeiből
kiderült, hogy az Ia SN-k maximális abszolút fényessége
legalább 1-1,5 magnitúdós szórást mutat, ami
nem a mérési hibából származik. Szerencsére az is bebizonyosodott,
hogy a maximális fényesség korrelál a SN-k
egyéb mérhető paramétereivel. Az egyik ilyen paraméter
a B-szűrős fénygörbe időbeli lefutása. Erre kétféle kalibrációs
eljárást is kidolgoztak. Az egyik a nyújtási módszer,
amely szerint az időtengely skálázásával ( a B-fénygörbék egymásra illeszthetők. Az s nyújtási paraméter
egyenesen arányos a maximális abszolút fényességgel
[1]. A
a B-fénygörbék egymásra illeszthetők. Az s nyújtási paraméter
egyenesen arányos a maximális abszolút fényességgel
[1]. A 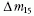 (B)-módszer
lényegében ugyanezt a
korrelációt alkalmazza, de itt a használt paraméter a
B-fénygörbe csökkenési üteme:
(B)-módszer
lényegében ugyanezt a
korrelációt alkalmazza, de itt a használt paraméter a
B-fénygörbe csökkenési üteme: 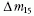 (B) a B-fényesség
maximumhoz képesti csökkenése magnitúdóban, a legnagyobb
fényesség után 15 nappal [3]. Az Ia SN-k abszolút
fénygörbéinek szórása mindkét módszerrel jelentősen
csökkenthető. E két módszer hátránya, hogy csak a
B-fénygörbére használható, amelynek mérése CCD-kamerákkal
problematikus, mivel a CCD-chipek inkább
vörösérzékenyek. Ezt küszöböli ki részben a többszínbeli
fénygörbealak (Multi-Color Light Curve Shape, MLCS)
módszer, amely a standard Johnson-féle B-, V-, R-, I -szűrőkön
át mért fénygörbék alakját használja fel a maximális
fényesség becsléséhez. Az előbbiektől eltérően ez
sokparaméteres kalibrációt igényel. Itt az illesztendő paraméter
(B) a B-fényesség
maximumhoz képesti csökkenése magnitúdóban, a legnagyobb
fényesség után 15 nappal [3]. Az Ia SN-k abszolút
fénygörbéinek szórása mindkét módszerrel jelentősen
csökkenthető. E két módszer hátránya, hogy csak a
B-fénygörbére használható, amelynek mérése CCD-kamerákkal
problematikus, mivel a CCD-chipek inkább
vörösérzékenyek. Ezt küszöböli ki részben a többszínbeli
fénygörbealak (Multi-Color Light Curve Shape, MLCS)
módszer, amely a standard Johnson-féle B-, V-, R-, I -szűrőkön
át mért fénygörbék alakját használja fel a maximális
fényesség becsléséhez. Az előbbiektől eltérően ez
sokparaméteres kalibrációt igényel. Itt az illesztendő paraméter
 , ahol
, ahol 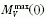 egy "normál" Ia SN V-szűrős abszolút fényessége maximumban. Kiderült,
hogy a különböző színbeli fénygörbék alakja és
egy "normál" Ia SN V-szűrős abszolút fényessége maximumban. Kiderült,
hogy a különböző színbeli fénygörbék alakja és  között többféle korreláció is fennáll:
között többféle korreláció is fennáll:
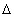 = +0,5, 0,0 és ?0,5
esetén.
A fenti korrelációk jelenleg teljesen empirikus alapon
állnak, bár történtek erőfeszítések ezek elméleti megalapozására.
Attól egyelőre nagyon távol vagyunk, hogy a
"normál" Ia SN-k maximális fényességét elméleti modellekből
kalibráljuk. Ezért az összes módszer empirikus
kalibrációt igényel: ismert távolságú (és vörösödésű)
SN-k halmazából kell megállapítani
= +0,5, 0,0 és ?0,5
esetén.
A fenti korrelációk jelenleg teljesen empirikus alapon
állnak, bár történtek erőfeszítések ezek elméleti megalapozására.
Attól egyelőre nagyon távol vagyunk, hogy a
"normál" Ia SN-k maximális fényességét elméleti modellekből
kalibráljuk. Ezért az összes módszer empirikus
kalibrációt igényel: ismert távolságú (és vörösödésű)
SN-k halmazából kell megállapítani  -ot, illetve kalibrálni
ennek korrelációját a többi paraméterrel (ez különösen
az MLCS-módszernél nehéz, hiszen ott teljes fénygörbéket
kell minden időpontra összeilleszteni). Az első
próbálkozások azon az elképzelésen alapultak, hogy a
kalibráló objektumok közeli, fényes SN-k legyenek, melyek
távolsága valamilyen független (pl. cefeidákon, vagy
Tully-Fisher-reláción alapuló) információ révén ismert.
Kiderült azonban, hogy csak nagyon kevés ilyen SN jöhet
szóba.
Az MLCS első kalibrációja például 9 objektumon
alapult [4], amelyek egyedi távolsága is csak pontatlanul
volt ismert. Ezért később áttértek a távoli, nagyobb vöröseltolódású
SN-k használatára, melyek relatív távolságát
a Hubble-törvény alapján sokkal pontosabban meg
lehet állapítani. Azonban ennek a megközelítésnek is
vannak hátrányai: egyrészt a távoli SN-k sokkal halványabbak,
emiatt fotometriájuk jóval pontatlanabb, másrészt
a nagyobb vöröseltolódásoknál a K-korrekció értéke
is jelentősebb, emiatt bizonytalanabb. Például egy z =
0,25 vöröseltolódású SN-nál a maximális fényesség idején
a K-korrekció V-szűrőben körülbelül ?0,4 magnitúdó,
ami már összemérhető az egyedi SN-k fényességdiszperziójával.
Az ennél is nagyobb vöröseltolódásoknál a méréshez
alkalmazott szűrő már a SN teljesen más spektrális
tartományát mintavételezi, mint a lokális objektumok
esetén. Például z = 0,4 körül az R-szűrő a SN nyugalmi
rendszerében körülbelül a B-szűrő spektráltartományára
eső fluxust méri, z > 1 esetén pedig az optikai tartományban
gyakorlatilag csak a SN ultraibolya fluxusa látszik. Ez
további problémákat okoz, mivel a SN-k U-szűrős fénygörbéiről
jóval kevesebb és pontatlanabb adattal rendelkezünk,
mint a többi hullámhossztartományról, ezért
nehéz bármivel is összevetni a mért fényességeket.
Sajnos mind a kalibrációt, mind a konkrét objektumok
távolságmérését számos egyéb körülmény nehezíti, melyek
oka részben méréstechnikai, részben az Ia SN-k még
nem kellően ismert fizikájában keresendő. Az első ilyen
probléma maga a fotometria. Az egyedi távcsövekkel,
szűrőkkel, detektorokkal végzett méréseket az úgynevezett
standard rendszerbe kell transzformálni annak érdekében,
hogy az alkalmazott műszerek átviteli függvényét
figyelembe vehessük a fotometria során. A standard
transzformációt csillagokra dolgozták ki, az összehasonlító
objektumok ismert spektrális tulajdonságú csillagok. A
SN-k spektruma viszont eltér a csillagokétól, különösen a
nebuláris fázisban. Az ilyen objektumok standard transzformációja
pontatlan lesz, a különböző műszerekkel
ugyanarról az objektumról készült mérések minimum 0,1
magnitúdó szórást mutatnak (problematikusabb esetekben
ez akár 0,2-0,3 magnitúdóra is nőhet). Ez a hiba azután
továbbterjed a távolságmérésre is. A másik technikai
nehézség a SN galaxisának jelenléte miatt lép fel. A SN
képe a galaxis képére rakódik rá, ami erős, inhomogén
háttérfényességet jelent a CCD-felvételen. Egy ilyen háttér
korrekciója igen nehéz. A legjobb módszer elvileg az,
hogy készítenek egy referenciaképet a galaxisról akkor,
amikor a SN nem látszik, és ezt a referenciaképet digitálisan
levonják a SN+galaxis képből. Ezzel az a probléma,
hogy ilyen kép a SN felfedezése előtt ritkán készül, tehát
meg kell várni, míg a SN teljesen elhalványul, és csak 1-2
évvel utána lehet a referenciaképet felvenni. Ezt igyekszik
kiküszöbölni az SZTE és az MTA Konkoly Thege
Miklós Csillagászati Kutatóintézet munkatársai által végzett
mérési program, amelynek célja ilyen referenciaképek
készítése a közeli galaxisokról [5].
Problémát jelent az Ia SN-kon belül a különleges (pekuliáris)
objektumok jelenléte is, melyek Ia típusúak, de
a "normálistól" eltérő spektrális jellemzőik vannak (5.
ábra). Ezek aránya a statisztikai becslések szerint akár
30-40% is lehet egy adott térfogati mintában. Az ilyen
SN-k két nagyobb csoportra oszthatók. Az SN 1991T-csoportba
tartozók a maximum környékén jóval kékebbek,
kevés spektrumvonalat mutatnak, és nagyobb luminozitásúak,
mint a "normál" SN-k. Az SN 1991bg-csoport tagjai
viszont 1-1,5 magnitúdóval halványabbak, több erős
spektrumvonalat mutatnak, és jóval gyorsabb a halványodási
ütemük is. Az eltérő spektrális jellemzők miatt ezen
objektumok nehezebben illeszthetők be a kalibrációs
sorozatba. Ismerünk olyan Ia-nak klasszifikált SN-t is
(SN 2002cx), amelynek teljesen egyedi jellemzői voltak,
egyetlen másik Ia SN-hoz sem hasonlítható fénygörbét és
spektrumot produkált. Ezen pekuliáris Ia SN-k fizikája
jelenleg nem kellően ismert, nem tudjuk, mi dönti azt el,
hogy egy fehér törpéből "normális", vagy pekuliáris SN
jön létre. Természetszerűleg az ilyen objektumok távolságmérése
is jóval bizonytalanabb.
Mindenfajta fotometriai információra alapuló távolságmérésnél
problémát jelent a csillagközi por okozta extinkció
és vörösödés. Habár az Ia SN-k vörösödésének
meghatározására létezik egy empirikus eljárás (lásd fentebb),
ennek eredményei legalább
-ot, illetve kalibrálni
ennek korrelációját a többi paraméterrel (ez különösen
az MLCS-módszernél nehéz, hiszen ott teljes fénygörbéket
kell minden időpontra összeilleszteni). Az első
próbálkozások azon az elképzelésen alapultak, hogy a
kalibráló objektumok közeli, fényes SN-k legyenek, melyek
távolsága valamilyen független (pl. cefeidákon, vagy
Tully-Fisher-reláción alapuló) információ révén ismert.
Kiderült azonban, hogy csak nagyon kevés ilyen SN jöhet
szóba.
Az MLCS első kalibrációja például 9 objektumon
alapult [4], amelyek egyedi távolsága is csak pontatlanul
volt ismert. Ezért később áttértek a távoli, nagyobb vöröseltolódású
SN-k használatára, melyek relatív távolságát
a Hubble-törvény alapján sokkal pontosabban meg
lehet állapítani. Azonban ennek a megközelítésnek is
vannak hátrányai: egyrészt a távoli SN-k sokkal halványabbak,
emiatt fotometriájuk jóval pontatlanabb, másrészt
a nagyobb vöröseltolódásoknál a K-korrekció értéke
is jelentősebb, emiatt bizonytalanabb. Például egy z =
0,25 vöröseltolódású SN-nál a maximális fényesség idején
a K-korrekció V-szűrőben körülbelül ?0,4 magnitúdó,
ami már összemérhető az egyedi SN-k fényességdiszperziójával.
Az ennél is nagyobb vöröseltolódásoknál a méréshez
alkalmazott szűrő már a SN teljesen más spektrális
tartományát mintavételezi, mint a lokális objektumok
esetén. Például z = 0,4 körül az R-szűrő a SN nyugalmi
rendszerében körülbelül a B-szűrő spektráltartományára
eső fluxust méri, z > 1 esetén pedig az optikai tartományban
gyakorlatilag csak a SN ultraibolya fluxusa látszik. Ez
további problémákat okoz, mivel a SN-k U-szűrős fénygörbéiről
jóval kevesebb és pontatlanabb adattal rendelkezünk,
mint a többi hullámhossztartományról, ezért
nehéz bármivel is összevetni a mért fényességeket.
Sajnos mind a kalibrációt, mind a konkrét objektumok
távolságmérését számos egyéb körülmény nehezíti, melyek
oka részben méréstechnikai, részben az Ia SN-k még
nem kellően ismert fizikájában keresendő. Az első ilyen
probléma maga a fotometria. Az egyedi távcsövekkel,
szűrőkkel, detektorokkal végzett méréseket az úgynevezett
standard rendszerbe kell transzformálni annak érdekében,
hogy az alkalmazott műszerek átviteli függvényét
figyelembe vehessük a fotometria során. A standard
transzformációt csillagokra dolgozták ki, az összehasonlító
objektumok ismert spektrális tulajdonságú csillagok. A
SN-k spektruma viszont eltér a csillagokétól, különösen a
nebuláris fázisban. Az ilyen objektumok standard transzformációja
pontatlan lesz, a különböző műszerekkel
ugyanarról az objektumról készült mérések minimum 0,1
magnitúdó szórást mutatnak (problematikusabb esetekben
ez akár 0,2-0,3 magnitúdóra is nőhet). Ez a hiba azután
továbbterjed a távolságmérésre is. A másik technikai
nehézség a SN galaxisának jelenléte miatt lép fel. A SN
képe a galaxis képére rakódik rá, ami erős, inhomogén
háttérfényességet jelent a CCD-felvételen. Egy ilyen háttér
korrekciója igen nehéz. A legjobb módszer elvileg az,
hogy készítenek egy referenciaképet a galaxisról akkor,
amikor a SN nem látszik, és ezt a referenciaképet digitálisan
levonják a SN+galaxis képből. Ezzel az a probléma,
hogy ilyen kép a SN felfedezése előtt ritkán készül, tehát
meg kell várni, míg a SN teljesen elhalványul, és csak 1-2
évvel utána lehet a referenciaképet felvenni. Ezt igyekszik
kiküszöbölni az SZTE és az MTA Konkoly Thege
Miklós Csillagászati Kutatóintézet munkatársai által végzett
mérési program, amelynek célja ilyen referenciaképek
készítése a közeli galaxisokról [5].
Problémát jelent az Ia SN-kon belül a különleges (pekuliáris)
objektumok jelenléte is, melyek Ia típusúak, de
a "normálistól" eltérő spektrális jellemzőik vannak (5.
ábra). Ezek aránya a statisztikai becslések szerint akár
30-40% is lehet egy adott térfogati mintában. Az ilyen
SN-k két nagyobb csoportra oszthatók. Az SN 1991T-csoportba
tartozók a maximum környékén jóval kékebbek,
kevés spektrumvonalat mutatnak, és nagyobb luminozitásúak,
mint a "normál" SN-k. Az SN 1991bg-csoport tagjai
viszont 1-1,5 magnitúdóval halványabbak, több erős
spektrumvonalat mutatnak, és jóval gyorsabb a halványodási
ütemük is. Az eltérő spektrális jellemzők miatt ezen
objektumok nehezebben illeszthetők be a kalibrációs
sorozatba. Ismerünk olyan Ia-nak klasszifikált SN-t is
(SN 2002cx), amelynek teljesen egyedi jellemzői voltak,
egyetlen másik Ia SN-hoz sem hasonlítható fénygörbét és
spektrumot produkált. Ezen pekuliáris Ia SN-k fizikája
jelenleg nem kellően ismert, nem tudjuk, mi dönti azt el,
hogy egy fehér törpéből "normális", vagy pekuliáris SN
jön létre. Természetszerűleg az ilyen objektumok távolságmérése
is jóval bizonytalanabb.
Mindenfajta fotometriai információra alapuló távolságmérésnél
problémát jelent a csillagközi por okozta extinkció
és vörösödés. Habár az Ia SN-k vörösödésének
meghatározására létezik egy empirikus eljárás (lásd fentebb),
ennek eredményei legalább 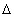 E(B-V) = ±0,1 magnitúdó
bizonytalanságúak (kb. ennyi az ismert, vörösödésmentes
SN-k B-V görbéjének szórása). A galaktikus
vörösödési törvény értelmében a V-szűrős fényességcsökkenés
AV = 3,1 E(B-V), amiből
E(B-V) = ±0,1 magnitúdó
bizonytalanságúak (kb. ennyi az ismert, vörösödésmentes
SN-k B-V görbéjének szórása). A galaktikus
vörösödési törvény értelmében a V-szűrős fényességcsökkenés
AV = 3,1 E(B-V), amiből
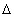 AV ~ 0,3 magnitúdó
bizonytalanság adódik. Ez szintén beépül a távolságmérés
hibájába. Ezért sokan próbálkoznak különböző alternatív
eljárásokkal, melyekkel igyekeznek a vörösödés
meghatározásának hibáját csökkenteni. Sajnos mindmáig
nincs teljes egyetértés abban, hogy mi lenne az igazán
megbízható eljárás.
Mindezen nehézségek ellenére 2004-ben Adam Riess
(STScI, USA) és munkatársai közzétették az általuk legmegbízhatóbbnak
értékelt Ia SN-k listáját, az úgynevezett
"arany mintát" (gold sample) [6]. Ezeket az MLCS-módszer
legújabb változatával analizálták, így egy homogén módon
meghatározott távolságskálát kaptak (igaz, itt is csak a
relatív távolságok tekinthetők kellően pontosnak, a távolságskála
zéruspontja változatlanul kérdéses). A 6. ábrán
látható ezen SN-k távolságmodulusa (1. képlet) a vöröseltolódás
függvényében. Folytonos vonallal az üres Univerzumban
érvényes luminozitási távolság van feltüntetve:
AV ~ 0,3 magnitúdó
bizonytalanság adódik. Ez szintén beépül a távolságmérés
hibájába. Ezért sokan próbálkoznak különböző alternatív
eljárásokkal, melyekkel igyekeznek a vörösödés
meghatározásának hibáját csökkenteni. Sajnos mindmáig
nincs teljes egyetértés abban, hogy mi lenne az igazán
megbízható eljárás.
Mindezen nehézségek ellenére 2004-ben Adam Riess
(STScI, USA) és munkatársai közzétették az általuk legmegbízhatóbbnak
értékelt Ia SN-k listáját, az úgynevezett
"arany mintát" (gold sample) [6]. Ezeket az MLCS-módszer
legújabb változatával analizálták, így egy homogén módon
meghatározott távolságskálát kaptak (igaz, itt is csak a
relatív távolságok tekinthetők kellően pontosnak, a távolságskála
zéruspontja változatlanul kérdéses). A 6. ábrán
látható ezen SN-k távolságmodulusa (1. képlet) a vöröseltolódás
függvényében. Folytonos vonallal az üres Univerzumban
érvényes luminozitási távolság van feltüntetve:

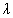 > 0 kozmológiai állandó kimutatása
[6]. A jelen tanulmánynak nem célja az ezzel kapcsolatos
eredmények minősítése, az azonban megfontolandó,
hogy a sokat idézett tudományfilozófiai kritérium,
miszerint an extraordinary claim requires extraordinary
evidence, a jelen kérdésben biztosan nem teljesül. Maguk
az idézett szerzők is korrektül elismerik, hogy a jelenlegi
ismereteinket tükröző SN-mintában még mindig sok a bizonytalansági
tényező, ezért a kozmológiai következtetéseknél
fennáll a túlinterpretálás veszélye.
Összegzésként ugyanakkor elmondható, hogy a szupernóvákkal
kapcsolatos ismereteink az elmúlt 10 évben
nagyságrendekkel bővültek, ennélfogva bizonyos, hogy
a további kutatások számos, jelenleg még ismeretlen,
illetve csak elnagyoltan ismert részletre derítenek majd
fényt. Erre a legnagyobb esélyt a tervezett SNAP űrtávcső
(SuperNova Acceleration Probe) jelentheti [7], melynek
felbocsátása 2010 körül várható.
Irodalom
> 0 kozmológiai állandó kimutatása
[6]. A jelen tanulmánynak nem célja az ezzel kapcsolatos
eredmények minősítése, az azonban megfontolandó,
hogy a sokat idézett tudományfilozófiai kritérium,
miszerint an extraordinary claim requires extraordinary
evidence, a jelen kérdésben biztosan nem teljesül. Maguk
az idézett szerzők is korrektül elismerik, hogy a jelenlegi
ismereteinket tükröző SN-mintában még mindig sok a bizonytalansági
tényező, ezért a kozmológiai következtetéseknél
fennáll a túlinterpretálás veszélye.
Összegzésként ugyanakkor elmondható, hogy a szupernóvákkal
kapcsolatos ismereteink az elmúlt 10 évben
nagyságrendekkel bővültek, ennélfogva bizonyos, hogy
a további kutatások számos, jelenleg még ismeretlen,
illetve csak elnagyoltan ismert részletre derítenek majd
fényt. Erre a legnagyobb esélyt a tervezett SNAP űrtávcső
(SuperNova Acceleration Probe) jelentheti [7], melynek
felbocsátása 2010 körül várható.
Irodalom