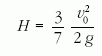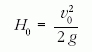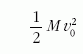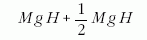Fizikai Szemle 2006/8 - 281.o.
139. PROBLÉMA
Egy fiatal eszkimó fókavadász az új szigonyát próbálgatja.
A kisméretű, de nehéz szigonyhoz a földön fekvő vékony,
hosszú, gondosan (gubancolódásmentesen) összetekert
lánc csatlakozik. Amikor az eszkimó függőlegesen
felfelé elhajítja szigonyát, az olyan magasra emelkedik,
hogy a róla lelógó lánc tömege éppen megegyezik a szigony
tömegével. Vajon hányszor magasabbra repülne az
ugyanekkora kezdôsebességgel függőlegesen feldobott
szigony, ha nem lenne hozzákötve a lánc?
(Varga István, Békéscsaba)
A 139. PROBLÉMA MEGOLDÁSA
Jelöljük a szigony tömegét M-mel, a lánc hosszegységre
jutó tömegét 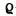 -val, a lánc pillanatnyi hosszát x-szel,
ennek az idő szerinti deriváltját, vagyis a szigony pillanatnyi
sebességét pedig v-vel! A lánc egyes darabkái úgy
jönnek mozgásba, hogy a már mozgó lánc újabb és újabb
szemeket ránt magával. Ez rugalmatlan ütközések sorozatán
keresztül valósul meg, melyeknél a mechanikai
energia nem marad állandó! Alkalmazható viszont az
impulzusváltozás Newton-féle törvénye:
-val, a lánc pillanatnyi hosszát x-szel,
ennek az idő szerinti deriváltját, vagyis a szigony pillanatnyi
sebességét pedig v-vel! A lánc egyes darabkái úgy
jönnek mozgásba, hogy a már mozgó lánc újabb és újabb
szemeket ránt magával. Ez rugalmatlan ütközések sorozatán
keresztül valósul meg, melyeknél a mechanikai
energia nem marad állandó! Alkalmazható viszont az
impulzusváltozás Newton-féle törvénye:
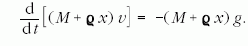
A bal oldalt átalakíthatjuk az alábbi módon:
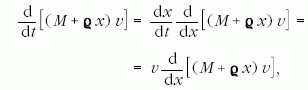
amit 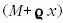 -vel megszorozva teljes deriváltat kapunk:
-vel megszorozva teljes deriváltat kapunk:
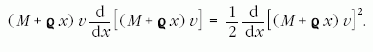
Integráljuk az
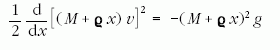
mozgásegyenletet x szerint a szigony v0 kezdősebességű
eldobásától az emelkedés teljes H magasságáig, ahol v = 0:
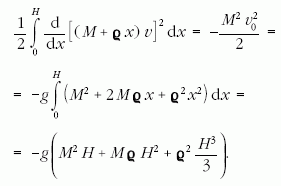
Kihasználva, hogy a feladat szövege szerint 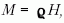 a
láncos szigony repülési magasságára végül
a
láncos szigony repülési magasságára végül
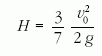
adódik. Ez az érték 7/3-szor kisebb, mint az ugyanekkora
kezdősebességhez tartozó láncnélküli eset
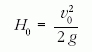
dobásmagassága.
A megoldásból az is leolvasható, hogy a láncos szigony
kezdeti
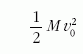
mozgási energiája nagyobb, mint a szigony megállásának
pillanatában számolható
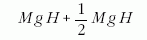
helyzeti energia; a mechanikai energiának 5/14-ed része,
mintegy 36 százaléka disszipálódott.
(V.I. )
140. PROBLÉMA
Egy hegyes ceruzát függőlegesen, a hegyével lefelé egy
vízszintes asztalra állítunk, majd elengedjük. A ceruza
valamerre eldől és az asztalhoz csapódik. Elmozdul-e a
dőlés közben a ceruza hegye, s ha igen, merrefelé?
(Varga István, Békéscsaba)
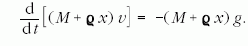
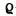 -val, a lánc pillanatnyi hosszát x-szel,
ennek az idő szerinti deriváltját, vagyis a szigony pillanatnyi
sebességét pedig v-vel! A lánc egyes darabkái úgy
jönnek mozgásba, hogy a már mozgó lánc újabb és újabb
szemeket ránt magával. Ez rugalmatlan ütközések sorozatán
keresztül valósul meg, melyeknél a mechanikai
energia nem marad állandó! Alkalmazható viszont az
impulzusváltozás Newton-féle törvénye:
-val, a lánc pillanatnyi hosszát x-szel,
ennek az idő szerinti deriváltját, vagyis a szigony pillanatnyi
sebességét pedig v-vel! A lánc egyes darabkái úgy
jönnek mozgásba, hogy a már mozgó lánc újabb és újabb
szemeket ránt magával. Ez rugalmatlan ütközések sorozatán
keresztül valósul meg, melyeknél a mechanikai
energia nem marad állandó! Alkalmazható viszont az
impulzusváltozás Newton-féle törvénye:
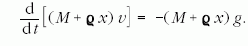
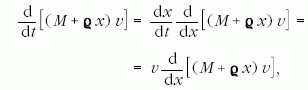
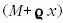 -vel megszorozva teljes deriváltat kapunk:
-vel megszorozva teljes deriváltat kapunk:
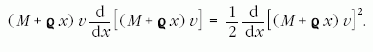
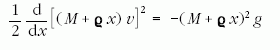
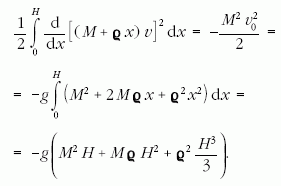
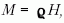 a
láncos szigony repülési magasságára végül
a
láncos szigony repülési magasságára végül