Fizikai Szemle 2006/9. 307.o.
IZGALMAS MÉRÉSEK A MÉRNÖK-FIZIKUS
HALLGATÓI LABORATÓRIUMBAN
Vankó Péter
BME, TTK, Kísérleti Fizika Tanszék
A kísérleti fizika laboratóriumi gyakorlatokon I-II. éves
mérnök-fizikus hallgatók a fizika legkülönbözőbb területeiről
összeválogatott mérési gyakorlatok keretében ismerkednek
a fizikai mérések, a számítógépes adatgyűjtés
és kiértékelés, valamint a hibaszámítás alapjaival. A legtöbb
hallgató mindenféle mérési tapasztalat nélkül érkezik
a középiskolából, de a háromórás mérések elvégzése,
a táblázatokat, képleteket, számításokat és grafikonokat
tartalmazó jegyzőkönyvek megírása a gyakorlattal rendelkezőknek
sem könnyű feladat.
A mérési gyakorlat megszerzéséhez lényegében bármely
mérés megfelelő lehet. A kísérletezésnek és a mérésnek
azonban a rutin megszerzése mellett nagyon fontos
szerepe van a fizikai szemlélet megalapozásában is.
Ehhez alapvető fizikai jelenségekhez kapcsolódó, a hallgatókat
motiváló, érdekes, izgalmas mérésekre van szükség.
A mérési feladatok korszerűsítésekor és új mérések
tervezésekor ez a pedagógiai szempont az elsődleges.
A két alapozó félév gyakorlatai, a mérések leírásai
megtalálhatóak az [1] internetcímen. Ebben az írásban két
olyan mérést ismertetek, melyek a fizika izgalmas, modern
területeit vizsgálják, ugyanakkor - a mérési feladat
szintjén - a kezdő, még csak minimális elméleti ismeretekkel
rendelkező hallgatóknak is érthetőek.
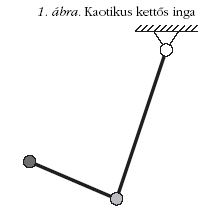
Kaotikus kettős inga vizsgálata V-scope-pal
Kettős ingát úgy készíthetünk, hogy egy fizikai inga végéhez
csuklóval egy másik fizikai ingát erősítünk (1. ábra).
A kettős inga az egyik legegyszerűbb mechanikai
rendszer, ami kaotikusan viselkedik. A kaotikus rendszer
viselkedése hosszú távon megjósolhatatlan. Ennek oka a
kezdőfeltételekre való rendkívüli érzékenység: ha a rendszert
a legcsekélyebb mértékben különböző kezdeti feltételekkel
hagyjuk magára, akkor véges időn belül teljesen
eltérően fog viselkedni. Ugyanakkor pontosan
ugyanazt a kezdőállapotot soha nem tudjuk megvalósítani.
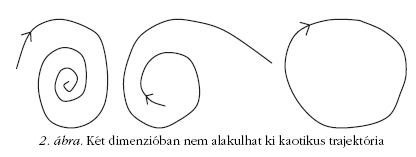
Mikor lehet egy rendszer kaotikus? Ha a rendszernek
legalább három szabad paramétere van, és a rendszert
leíró egyenletek nemlineáris tagot is tartalmaznak [2]. A
legalább három szabad paraméter azért szükséges, mert
ekkor a fázistérben kialakulhat olyan trajektória, amely
nem tart sem egy véges ponthoz, sem a végtelenbe, és
ugyanakkor soha nem záródik. Két dimenzióban ez nem
lehetséges (2. ábra).
A kaotikus kettős inga mozgása nagyon látványos,
ezért gyakran bemutatják. Ha a rendszer kezdő energiája
elég nagy, az alsó "kis kar" - teljesen váratlanul - többször
is körbefordulhat. Mérés nélkül is jól látszik, hogy a
megismételt, a lehető legpontosabban ugyanonnan elindított
mozgások jelentősen különbözőek.
A kettős inga kaotikus viselkedését számítógépen is
lehet szimulálni. Az interneten rengeteg ilyen program
található (és a hallgatók is nagyon szép programokat
készítettek a laborhoz lazán kapcsolódó szorgalmi feladatként).
Természetesen - szemben a valósággal - a
számítógép tökéletesen meg tudja ismételni a korábbi
futást. Itt a kezdőállapot kis különbségét (vagy a mozgást
zavaró kis zajokat) és a súrlódásból, légellenállásból
adódó csillapodást mesterségesen kell beépíteni a programba.
A szimuláció érdekes és hasznos kiegészítése
lehet a mérésnek, de valódi mérés nélkül akár szemléletromboló
is lehet, hiszen a számítógépen bármit be lehet
programozni, függetlenül a valóságtól. A kaotikus viselkedés
vizsgálatához és megértéséhez fontos a kvantitatív
mérés! Valódi mérésről - a szimulációkról szólókkal
szemben - csak kevés cikk számol be. Az ingakarok
szögelfordulását lehet mérni a csapágyakba beépített
potenciométer segítségével [3], vagy a mozgás stroboszkopikus
fényképezésével [4]. Iskolai vagy egyetemi tanterv
szerint, rendszeresen végzett mérésről - az itt ismertetetten
kívül - nincs tudomásom.
Ismerkedés a V-scope mérőrendszerrel
A BME mérnök-fizikus hallgatói laboratóriumában a kaotikus
kettős inga mérése V-scope segítségével történik. A
V-scope térben mozgó testek mozgását követi nyomon: a
kísérletben részt vevő testek háromdimenziós koordinátáit
méri és rögzíti az idő függvényében. A V-scope három
"torony"-ból, a vizsgált testekre rögzített "gombocskák"-
ból és egy mikroszámítógépből áll. Az infravörös
jellel aktivált "gombocskák" ultrahangot bocsátanak ki. A
"tornyok" mérik az ultrahangjel beérkezési idejét, a mikroszámítógép
ebből a hang terjedési sebességének ismeretében
határozza meg a "gombocskák" térbeli helyzetét.
A mért adatok a rendszerhez tartozó szoftverrel megjeleníthetők,
vagy további adatfeldolgozáshoz kimenthetők.
(A V-scope működéséről [6] és felhasználásáról [6, 7]
több írás is megjelent a Fizikai Szemlében.)
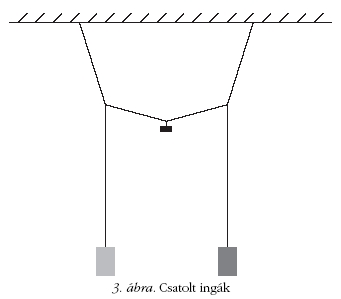
A hallgatók a V-scope-pal már a kaotikus kettősinga
vizsgálata előtt, egy másik mérésben megismerkednek.
Ebben a Szegedi Tudományegyetem hallgatóinak méréséhez
[7] hasonlóan csatolt ingák mozgását tanulmányozzák
(3. ábra). Az általam összeállított mérés - a szegedi
méréssel ellentétben - kihasználja, hogy a V-scope három
dimenzióban képes a nyomkövetésre: így az ingák
mozgását nemcsak a csatolással párhuzamos, hanem a
csatolásra merőleges irányban is mérni lehet. A csatolatlan
inga, a csatolatlan kúpinga mérése után a csatolással
párhuzamosan és a csatolásra merőlegesen kitérített csatolt
ingák mérése következik (csatolási állandó mérése a
csatoló tömeg függvényében). Itt csak az utolsó, leglátványosabb
mérés eredményét mutatom be: csatolt kúpingák
mozgása.
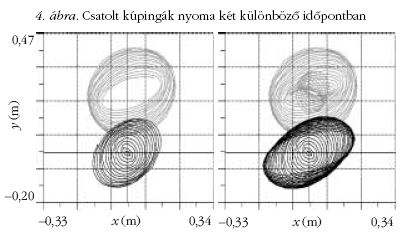
A 4. ábrán a két inga vízszintes pályája látható (alulnézetben:
a "tornyok" az ingák alatt, a földön elhelyezve,
felfelé "nézik" az ingák aljára rögzített "gombocskákat").
Az ábra két része ugyanazt a mozgást ábrázolja két különböző
időpontban megállítva. Kezdetben az ábrán felül
látszó (halványabban ábrázolt) ingát kúpingaként indítottuk
el, míg a másik inga állt. Az x és y irányú csatolási
állandók különbözősége miatt a körpályák ellipszisalakúvá
válnak. Ráadásul a csatolási állandók különbözősége
miatt az x és y irányú periódusidők is kismértékben különböznek,
ezért az ellipszisek lassan el is fordulnak.
A kaotikus kettős inga mérése
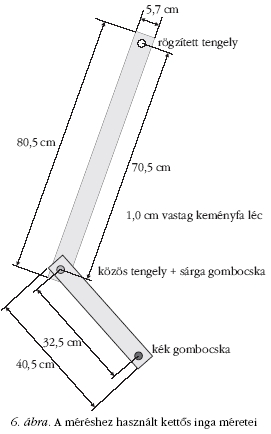
A méréshez használt kettős inga képe az 5. ábrán, méretei
a 6. ábrán láthatóak. A keményfából készült kettős
inga rögzített csapágya egy stabil öntöttvas állványra van
felszerelve. A "gombocskák" a két ingakart összekapcsoló
csapágynál (a nagy kar végén) és az alsó (kis kar) végpontjában
vannak. Az origó a rögzített tengelyhez van
beállítva. A tornyok, a mikroszámítógép és a számítógép
a kettős ingától körülbelül 3 méter távolságra, egy asztalon
vannak felállítva (7. ábra). A mérési gyakorlat során
7 különböző (egyre nagyobb kezdeti energiájú) helyzetből
kell elindítani a kettős ingát - minden helyzetből
(amilyen pontosan csak lehet, ugyanonnan) egymás után
négyszer.
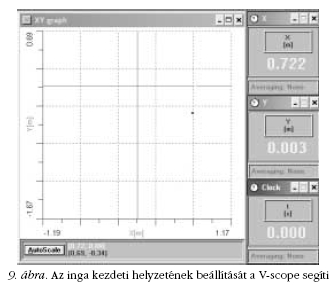
A 8. ábrán az egyik indítási helyzet látható (a nagy
kar vízszintes, a kis kar szabadon lóg). Az indítási helyzet
beállítása is a V-scope segítségével történik: a 9. ábrán
látható a számítógép képernyője az indítás pillanatában.
A grafikon melletti "műszereken" a (nagy kar végére szerelt)
"sárga gombocska" koordinátái (és az idő) láthatóak
- a kezdeti helyzetet ezek segítségével lehet beállítani.
Mivel a V-scope az egész mozgást (a beállítást és a vizsgált
kaotikus mozgást is) rögzíti, a mérés után a szabad
mozgás előtti részt le kell vágni.

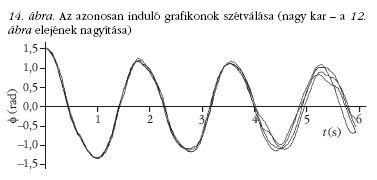
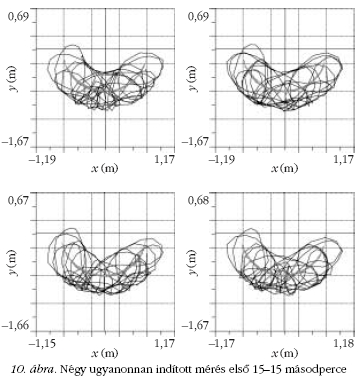
A 10. ábrán látható a négy "azonos" helyről (8.
ábra ) indított mozgás első 15-15 másodpercének grafikonja.
A kicsit halványabb, félkör alakú vonal értelemszerűen
a nagy kar végének ("sárga gombocska"), míg a
sötétebb, szabálytalan vonal a többször körbeforduló
kis kar végpontjának ("kék gombocska") a nyoma.

A mérési adatok feldolgozása
A V-scope-hoz tartozó szoftverrel egyszerre csak egy
mérés ábrázolható, elemezhető. A négy "azonos" helyről
indított mozgás összehasonlításához az adatokat más
programok által is használhatóvá kell tenni. Sajnos a
szoftver által kínált adatexportálási lehetőség ilyen nagy
adatállományok esetében nem működik (a program "lefagy").
Szerencsére a V-scope által tárolt .vsw és .ves kiterjesztésű
fájlok elég könnyen megfejthető formátumban
tárolják az adatokat, így azok egy egyszerű pascal programmal
könnyen .txt formátumú fájlokká alakíthatóak,
melyekben a két gombocska x, y és z koordinátái, valamint
az időadatok szerepelnek.
A hallgatóknak ezekből az adatokból kell mindkét
karra szögelfordulás-idő grafikonokat készíteniük. A
feladatot a kis kar esetében több körülmény is nehezíti. A
kis kar két végpontjának koordinátáit a V-scope nem
egyszerre, hanem felváltva méri - emiatt a lassabban
mozgó vég koordinátáit a megfelelő időpillanatban interpolációval
kell meghatározni. A kis kar többször is körbefordulhat
a mozgás során - ezeket az átfordulásokat
megfelelően kezelni kell. A hallgatók szabadon választhatják
meg a számításokhoz az eszközöket: a feladat pascal
vagy C programmal és excel táblázatkezelővel is megoldható.
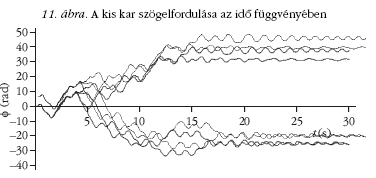
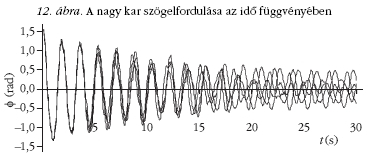
A 11. és 12. ábrán a kis kar és a nagy kar szögelfordulása
látható az idő függvényében. Mindkét grafikonon
látható, hogy a görbék vonalvastagságon belül ugyanúgy
indulnak, de körülbelül 4 másodperc után szétválnak
egymástól. A kis kar elfordulását ábrázoló grafikonon
különösen feltűnő a különbség: az egyes mérések végállapotai
között 60-65 rad (10 teljes körbefordulás!) különbség
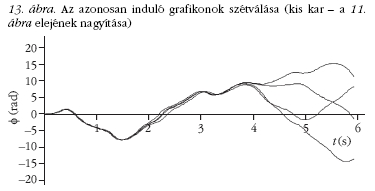
is lehet. A 13. és 14. ábrán a mozgás első 6 másodperce
látható kinagyítva: itt még jobban megfigyelhető
a szétválás folyamata.
A mérési feladat 7 ilyen grafikonpár megrajzolása és a
szétválás idejének meghatározása (különböző kezdőállapotból
induló mozgások esetén). Kis kezdeti energiáknál,
amikor a kis kar nem tud átfordulni, a kaotikus jelleg
nem, vagy csak kevéssé figyelhető meg. A kaotikus mozgás
részletesebb vizsgálatához (például a Ljapunov-exponens
meghatározásához) a másodéves hallgatók még
nem rendelkeznek előismeretekkel, így az természetesen,
nem is feladat.

Granulált anyagok vizsgálata
A granulált (szemcsés, granuláris) anyagok nagyszámú,
szilárd szemcséből állnak. A természetben és az ipari
gyakorlatban nagyon sok egymástól különböző anyag
tartozik ebbe a csoportba a néhány mikrométeres festékporoktól
a kőomlások méteres nagyságú szikladarabjaiig,
a szabályos kis golyóktól a teljesen szabálytalan, szögletes
formákig. Meglepő, látványos viselkedésükre még
csak részben sikerült elméleti magyarázatot találni [8, 9].
Rézsűszög és szegregáció
Ha a kohézió (száraz anyag esetében) elhanyagolható, akkor
a granulált anyag egyensúlyát a gravitáción kívül kizárólag
a szemcsék közti és a külső határoló felületek által
kifejtett nyomó és súrlódási erők határozzák meg. A probléma
ennek ellenére nagyon bonyolult: nemcsak a szemcsék
nagy száma és általában szabálytalan alakja, hanem a
tapadási súrlódási erők következtében létrejövő befeszülések,
beékelődések miatt is. A nyugalomban lévő granulált
anyag termodinamikai szempontból tipikus nemegyensúlyi
rendszer. A lehetséges minimális értéknél jóval
nagyobb potenciális energiájú elrendeződések is "befagyhatnak",
hiszen az atomi méreteknél jóval nagyobb szemcsék
aktiválásához szobahőmérsékleten a termikus gerjesztés
nagyon kevés, a külső mechanikai hatások megszűnése
után a szemcsék rugalmatlan ütközései pedig
hamar felemésztik a rendszer kinetikus energiáját.
A granulált anyagok sztatikájának legegyszerűbb kísérleti
vizsgálata a rézsűszög mérése. A mérés első felében
két párhuzamos plexilap közé tölcséren át különféle homogén
és kevert granulált anyagokat öntenek a hallgatók
(15. ábra). Bár a granulált anyagok a folyadékokhoz
hasonlóan önthetőek, az edényben nem terülnek teljesen
szét, hanem az anyag minőségétől (valamint a két lap
távolságától, az öntés sebességétől) függő meredekségű
lejtőt alkotnak. A lejtő - többé-kevésbé egyenes - vonalának
a vízszintessel bezárt szöge a rézsűszög. A 16.
ábrán egy (pirosra festett) díszhomok aránylag meredek,
a 17. ábrán apró, közel gömb alakú (világossárga) üveggyöngyök
sokkal laposabb rézsűje látható. A rézsűszög
könnyen mérhető.
A mérés izgalmasabb és látványosabb része a keverékek
viselkedése. Már az öntés előtt furcsa jelenséget lehet
megfigyelni: rázás hatására a keverék két komponense
általában nem összekeveredik, hanem szétválik. (Összekeverni
- úgy-ahogy - legfeljebb egy kiskanállal lehet.) A
különböző alakú, méretű, sűrűségű szemcsék spontán
szétválása a szegregáció. A keverékek beöntésekor a különböző
méretű és alakú (különböző rézsűszögű)
szemcsék másképp gurulnak le a lejtőn, és emiatt - nem
túl gyors beöntés esetén - többé-kevésbé szabályos rétegekbe
rendeződnek. A 15. és 18. ábrán az előbb bemutatott
piros homok - sárga üveggyöngy keverék beöntésekor
kialakuló mintázat látható. A rétegek úgy jönnek
létre, hogy az egyik anyag lavinaszerűen legurul a másikon,
majd alulról felépít egy réteget. A 18. ábrán felül jól
látszik egy, a beöntés végén félbemaradt lavina. A 19.
ábrán mák és játszótéri homok az előzőhöz hasonló
szegregációja látható. A beöntési sebességtől is erősen
függő rétegvastagság akár a helyszínen, akár a fényképeken
egyszerűen mérhető.

Mintázatképződés
A granulált anyag folyamatosan mozgásban tartható, ha a
szemcsék rugalmatlan ütközése során elvesző (elsősorban
hővé alakuló) energiát külső mechanikai gerjesztéssel
(rázással, keveréssel, öntögetéssel stb.) folyamatosan
pótoljuk. A mérés második részében granulált anyag rázásakor
kialakuló mintázatok vizsgálata a feladat. A rázás
hatására, ha a maximális gyorsulás nagyobb, mint a g
nehézségi gyorsulás, a szemcsék egymáshoz képest is
mozogni kezdenek, egymással és az edény falával ütköznek,
az ütközések között pedig a gravitáció és a közegellenállás
által meghatározott pályán repülnek.

Egyetlen szabadeséssel függőlegesen mozgó és egy
harmonikusan rezgő vízszintes lemezzel ütköző golyó
mozgásának leírása se könnyű, hiszen a kialakuló mozgás
nem periodikus. Nagyon nagy számú szemcse háromdimenziós
mozgása (amit kis szemcseméret esetén a
közegellenállás is jelentősen befolyásol) és (az általában
szabálytalan alak miatt) bonyolult ütközései teljesen kiszámíthatatlan
mozgást sejtetnek. Ezzel szemben a tapasztalat
szerint a szemcsék rezgetésekor gyakran többé-kevésbé
szabályos mintázatok keletkeznek. Miközben az
egyes szemcsék mozgása hosszú távon valóban teljesen
megjósolhatatlan, a sokaság kollektív mozgása mégis
rendezettnek tűnik. A szemcsék tulajdonságainak, a
rázott granulált anyag mennyiségének, valamint a rázási
frekvenciának és az amplitúdónak függvényében nagyon
változatos formák jelenhetnek meg: állóhullámok, négyszöges
és hatszöges mintázatok, örvénylés, "fortyogás",
dombképződés stb.
A mérési feladat a mintázatok megfigyelése és feltérképezése
a maximális gyorsulás-frekvencia (a- f ) fázistérben.
A mérési berendezés a 20. ábrán látható: a rázógép
függőleges tengelyű hengeres műanyag edényét egy
hangszórómembrán hozza függőleges irányú rezgőmozgásba.
A rezgés frekvenciája és amplitúdója a hangszórómembránra
kapcsolt szinuszos jel frekvenciájától és
nagyságától függ. Az edény gyorsulását egy gyorsulásmérő
csip méri (a képen egyelőre csipesszel rögzítve az
edényhez). A mérési gyakorlat során 0,15 mm átmérőjű
üveggyöngy 1 és 3 mm vastag rétegét, valamint homokot
rezgetnek a hallgatók. A mintázatképződés a 10-30 Hz
frekvencia- és 1g -5g gyorsulástartományban figyelhető
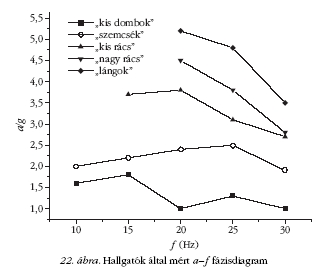
meg. A 21. ábra hat darab fényképén jellegzetes mintázatok
láthatók, a 22. ábrán pedig egy, a hallgatók által
kimért fázisdiagram.
Tapasztalataink szerint a hallgatók szeretik ezeket a
méréseket. Sokan szívesen fordítanak a kötelezőnél több
időt és energiát a mérés elvégzésére és a jegyzőkönyv
elkészítésére is. A szokatlan és izgalmas feladatok gyakran
a kevésbé érdeklődő hallgatókat is fellelkesítik, és
elkezdenek "játszani".
Irodalom
- Kísérleti fizika labor I-II. http://goliat.eik.bme.hu/~vanko/labor/labor.htm
- TÉL T., GRUIZ M.: Kaotikus dinamika - Nemzeti Tankönyvkiadó,
Budapest, 2002.
- BÉKÉSSY L.I., BUSTYA Á.: Fizikai kettősinga vizsgálata - Fizikai
Szemle 55 (2005) 185
- T. SHINBROT, C. GREBONI, J. WISDOM, J.A. YORKE: Chaos in a double
pendulum - Am. J. Phys. 60 (1992) 491
- M. RONEN, A. LIPMAN: A vektorszkóp - háromdimenziós mozgások
nyomonkövetése és elemzése - Fizikai Szemle 45 (1995) 395
- ERLICHNÉ BOGDÁN K., DEDE M., DARAI J., DEMÉNY A.: Hely- és időmérés,
adatfeldolgozás V-scope és számítógép alkalmazásával - Fizikai
Szemle 55 (2005) 213
- FARKAS ZS.: A vektorszkóprendszer alkalmazása a kinematikában -
Fizikai Szemle 54 (2004) 345
- JÁNOSI I.: A homok titkai - Természet Világa 129 (1998) 19
- JÁNOSI I.: Zajongó homokdombok és egyéb furcsaságok: új fejlemények
a granuláris anyagok fizikájában - Fizikai Szemle 45
(1995) 78