Fizikai Szemle 2007/1. - Papp Katalin, Nagy Anett: Public relation és a fizikatanítás

PUBLIC RELATION ÉS A FIZIKATANÍTÁS - avagy hogyan tegyük vonzóvá a fizika tantárgyat

Papp Katalin, Szegedi Tudományegyetem, Kísérleti Fizikai Tanszék
Nagy Anett, Radnóti Miklós Kísérleti Gimnázium, Szeged

"Az iskola arra való, hogy az ember megtanuljon tanulni, hogy felébredjen tudásvágya, megismerje a jól végzett munka örömét, megízlelje az alkotás izgalmát, megtanulja szeretni amit csinál, és megtalálja azt a munkát, amit szeretni fog."

Szent-Györgyi Albert

OK! Megtanulom a fizikát, de mit kapok érte? - teszi fel a kérdést egy 14 éves diák. - Gyerekem, bár tudom, hogy szereted a fizikát, mégis inkább válaszd a közgazdász pályát, a mai világban többre mégy vele! - mondja a szülő a pályaválasztás előtt álló fiatalnak.

- Miért ne hagyjam, hogy süsse a Nap? - kérdezi a bankkártyáját, mobiltelefonját virtuózmódon használó fiatal.

Sorolhatnánk tovább azokat a naponta elhangzó kijelentéseket, amelyek a természettudományos tantárgyak kedvezőtlen tanulói megítélését, a fiatalok természettudományos pályáktól való elfordulását, a természettudományos tudásszint csökkenését illusztrálják. A kilencvenes években erősödött föl ez a kedvezőtlen tendencia, és az összetett jelenséget befolyásoló tényezők hatását vizsgáló kutatások eredményei ma már a nemzetközi és hazai tantárgy-pedagógiai szakirodalomban nagy számban megtalálhatók (TIMSS, PISA és hazai vizsgálatok, [1-7]).

Írásunkban azokat az általunk kifejlesztett, kipróbált lehetőségeket, konkrét stratégiákat mutatjuk be, amelyek a természettudományos ismeretek társadalmi megítélését, a fiatalok természettudományos attitűdjét reményeink szerint kedvezően befolyásolják. Meggyőződésünk, hogy a hasznosítható természettudományos tudás, a mindenki számára szükséges releváns természettudományos műveltség iskolán belüli terepe mellett fokozott figyelmet kell fordítani az iskolán kívüli környezetre is. Fejlesztéseinknél kiindulási elvként használtuk föl az átalakuló természettudományos nevelés főbb ismérveit.

Megváltozott a természettudományos tanítás filozófiája, szemlélete, amely szerint az iskolai természettudományos oktatás célja (az elitképzést leszámítva) nem az, hogy valamennyi tantárgy esetén tudományos alapképzést adjon, hanem az, hogy a hétköznapi életben biztonsággal eligazodó, kompetens személyiségeket képezzen, és ehhez használható ismereteket nyújtson. Az iskolából kikerülő fiatalokkal szemben ma már nem az az elvárás, hogy az iskolában szerzett szakmai és elméleti tudásuk alapján a (lehetőleg az első és egyetlen) munkahelyükön minél tovább helytálljanak, hanem az, hogy a naponta megújuló feladatok megoldása érdekében képesek legyenek ismereteiket rendszeresen felfrissíteni, magukat az életük során akár többször is, többféle munkakör ellátására átképezni. Az oktatásnak, így a természettudományos oktatásnak is fel kell készítenie a tanulókat arra, hogy egészéletükön át képesek legyenek valamennyi új technikai és tudományos kihívással felkészülten szembenézni. Marx György szerint "ezt egyetlen más tantárgy sem vállalhatja fel, a természettudománynak tehát kiemelten fontos alaptantárgynak kell lennie. A legfőbb cél az, hogy a saját világában eligazodó, azt összetettségében értő, s egyben kritikusan szemlélő, felelősen gondolkodó és döntő felnőtteket neveljünk." [8]

Célkitűzéseink szerint kutatásunkban tudatosan összekapcsoltuk a tananyagot a mindennapos tárgyakkal, jelenségekkel. Ez a természettudományos tanításban triviálisnak tűnő módszer segíthet abban, hogy megszűnjön a szakadék az iskolában megszerzett tudás és a tanulók iskolán kívüli mindennapos tapasztalatai között, amelyet a szakirodalomban többen is megfogalmaztak:

"az ismeretek csak iskola szituációban muködnek, a tudás a mindennapokban nem használható" (Radnóti Katalin [9])
"a tudományos ismeretek gyakorlati alkalmazása nem hatékony" (B. Németh Mária [5]) "az iskolai tananyag elszakad a tanulók számára ismert és közvetlenül megtapasztalható jelenségektől ...." (Korom Erzsébet [5])

További jellemzők, hogy a stratégiák kiemelten támaszkodnak a tanulók aktivitására (egyéni és csoportos egyaránt) és iskolán kívüli környezetben valósulnak meg. Fejlesztéseinket, amelyekből az alábbiakban jellegzetes példákat válogatunk, csoportokba sorolhatjuk.

Irányított tanulói megfigyelés

Természeti, technikai környezetünk tele van olyan jelenségekkel, gyakorlati alkalmazásokkal, amelyekre ráirányítva a tanulók figyelmét - kirándulásokon vagy akár múzeumi vagy tárlatlátogatáson - jó alkalom adódik a fizikai ismeretek közvetlen megtapasztalására. Például a hőtan tanításánál, a hőtágulás törvényének megfigyeléséhez jó alkalmat kínálnak a vasúti sínek, a lazán rögzített elektromos vezetékek, a hidak felfüggesztésének, a távfűtés csöveinek speciális formájú elrendezései (1. ábra).

Tárlatlátogatáson a képzőművészeti alkotások megtekintése mellett az igényes kivitelű csillár szépen csiszolt függelékei a fénytörés jelenségének közvetlen megtapasztalását segíthetik (2. ábra).

Mérések terepen

A fizikai mennyiségek mérése, a fizika mérőtudomány jellegének bemutatása nem csak az iskolai előadóteremben lehetséges. Például a sebesség fogalmának kialakításához, méréséhez ad segítséget az alábbiakban részletezett egyszerű "utcai" sebességmérés.

Sebességmérés terepen
A tanulók feladata: az utcai járműforgalom átlagos sebességének meghatározása egy kijelölt útszakaszon. A vizsgálat célja annak megállapítása, hogy a két egymás mellett található iskola előtti egyenes útszakaszon (~200 m) közlekedő autók betartják-e az előírt sebességkorlátozást (3. ábra).

A csoportokba szerveződött diákok biciklikerék, jelző zászlók, stopper segítségével mérik az autók sebességét. Ugyancsak jól használható erre, ahogy a mozgások elemzéséhez általában is, a digitális fényképezőgép. A mérés eredménye: az átlagos sebesség 56 km/h. Közösen levelet fogalmaztak meg a Rendőrfőkapitányság Közlekedésfelügyeleti Osztályának, és kérték a gyerekforgalomra figyelmeztető tábla kihelyezését.

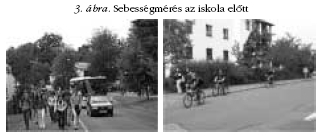
A szabadesésre vonatkozó formulák alkalmazására mutathatunk példát egy híd vagy egy fa magasságának lemérésével, az itt nem részletezett, de már Öveges tanár úr könyveiben is megtalálható ejtési, illetve hajítási kísérletekkel.

Próbáld ki, mérd meg otthon!

A tanulók érdeklődését felkeltő, vonzó témájú és pontosan megfogalmazott otthon elvégezhető kísérletek, mérések nemcsak szakmai haszonnal járnak, hanem a tanulók önállóságát, kreativitását, kísérletező készségét is fejlesztik, nem beszélve a "burkolt óraszámnövelő" hatásukról. Az alábbiak példák arra, hogy egy-egy problémát különböző szinten, a differenciált foglalkoztatást megvalósítva dolgozhatnak fel a diákok.

Interferencia vékony rétegen
("Körömlakk-szivárvány")
Egy edénybe öntsünk vizet, és az aljára fektessünk egy fekete kartonlapot. Cseppentsünk egy nagyobb csepp színtelen körömlakkot (körömerősítőt) a vízbe, a víz felszínéhez nagyon közelről. Ez a csepp vékony, kör alakú bevonatot képez majd a víz felszínén, ami néhány perc várakozás után a szélekről kiindulva megszárad. Ekkor óvatosan emeljük ki a kartonlapot ügyelve arra, hogy a vékony körömlakkréteg a papírra ragadjon, és rajta is maradjon. Hagyjuk megszáradni az átázott papírt (pl. újságpapíron). Szebbnél szebb, a szivárvány színeiben pompázó lakkrétegeket kapunk (4. ábra).

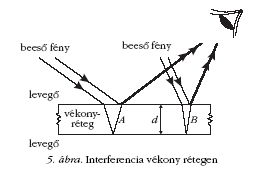
A jelenség a fény interferenciájának eredménye. Tekintsünk egy fénytörő vékony réteget. A ráeső fény mind a felső mind az alsó felületéről visszaverődhet. Az 5. ábra a két helyről visszaverődő fehér fény sugármeneteit mutatja. A visszavert fénysugarak mindkét helyről a megfigyelő szemébe jutnak és interferálnak egymással. Bizonyos hullámhosszakra az erősítés, másokra a gyengítés feltétele teljesül. Példaként foglalkozzunk azzal az esettel, amikor a vörös fény teljesen kioltódik. Ekkor a megfigyelő túlnyomóan kékzöld színű hullámok visszaverődését fogja látni azon a helyen. Másrészt, ha a B pontban az útkülönbség rövidebb, a megfigyelő túlnyomó részben a vöröses fény visszaverődését látja. Így a szivárvány minden színe megjelenhet a vékony réteg különböző részeiről visszaverődve. Ahol azonban a hártya vékonyabb a látható fény hullámhosszánál, a rétegről egyáltalán nem verődik vissza fény, láthatatlanná válik. Ennek oka az, hogy az első és hátsó felületekről visszaverődő fény kioltja egymást, mert a nagyobb törésmutatójú közeg határáról történő visszaverődés során a fázis 180°-kal ugrik, míg a kisebb törésmutatójú közeg határáról történő visszaverődés során fázisugrás nem lép fel. A megszáradt körömlakkréteg nem egyforma vastagságú a víz felszínén. A réteg a szélén elvékonyodik, míg a belsejében egyre vastagabb. A körömlakkréteg törésmutatója pedig függ a ráeső fény hullámhosszától. A megszáradt körömlakk törésmutatója 1,42 körüli érték.

Buborék mozgásának vizsgálata
Az egyszerű eszközökkel végzett kísérletek az iskolán kívül is segíthetnek a fizika népszerűsítésében. Ezt már sokan és régen felismerték. Erre jó példa lehet a következő kísérlet, amely egy 1893-ban kiadott könyvből származik [10]. A kor hangulatát és beszédstílusát felelevenítve eredeti szövegével is bemutatható és magyarázható a kísérlet.

"Vidám lakoma végén, mikor a pezsgős palackok szaporán ürülnek és szítják a jókedvet, ajánlkozzál, hogy fölidézed a társaság megrettentésére magát a Sátánt, mégpedig anélkül, hogy a középkorban dívott hókuszpókuszhoz folyamodnál. A csemegés tálból keress ki egy nagyobb szem jó száraz malagaszőlőt, tölts egy poharat tele pezsgővel és ejtsd bele a malagaszőlő szemet. Csakhamar megindul a produkció. A pezsgőborból kifejlődő szénsav apró buborékokban lepi el a szőlőszemet s olyan hatással van rá, mintha valamely tárgyat léggömbök emelnének föl. Néhány másodperc alatt a szénsavbuborékok fölemelik a szőlőszemet a pohár felszínére. A szőlőszemről azonban, mihelyt a pohár felszínére ér, elillannak a szénsavbuborékok, a szőlőszem visszanyeri súlyát és lemerül a pohár fenekére. A pohár mélyén a szénsavbuborékok aztán újra megkönnyítik a szőlőszemet, az újra felemelkedik, aztán megint lemerül s ez a hintázás eltart vagy tízpercig, amíg tudniillik a pohárban levő pezsgőből a szénsav mind el nem szállt." (6. ábra) Ez a látszólag egyszerű jelenség számos kérdést vet fel. Mitől "pezseg" a pezsgő? Mitől alakulnak ki a buborékok a pezsgőben, és miért alkotnak hosszú láncot miközben a felszínre jönnek? Milyen törvények írják le a buborékok mozgását?

Az első kérdésre az a válasz, hogy a pezsgő oldott szén-dioxidot tartalmaz, méghozzá magasabb koncentrációban, mint a folyadék feletti levegő. A gyártás során a 2-5 · 10⁵ Pa nyomáson megtöltik szén-dioxiddal az üveget, majd beletöltik a folyadékot (pezsgő, ásványvíz, üdítő). A gázok oldódási képessége növekszik a felette levő gáz nyomásának növelésével. A zárt, feltöltött üvegben a folyadék felszíne felett dinamikus egyensúlyi állapot alakul ki a folyadékban oldott és a gázállapotú CO₂ között. Minél hidegebb az üdítő vagy a sör, annál nagyobb az oldott állapotú CO₂ mennyisége. Amint felnyitjuk az üdítős üveget, az egyensúly felborul és az oldott állapotú gázfokozatosan elhagyja a folyadékot buborékok formájában.

A második kérdés megválaszolásához figyeljük meg a buborékképződés mechanizmusát. A folyadék belsejében a gázapró buborékokban gyűlik össze, amelyek elérve egy bizonyos kritikus méretet feljönnek a felszínre. A buborékok azonban nem a folyadék belsejében keletkeznek, hanem a pohár belső felületén bizonyos pontokban. A felszín mikroszkopikusan kicsiny sérüléseiben megfelelőek a feltételek a buborékképződéshez. A mazsola, földimogyoró vagy más tárgyak - szabálytalan felszínük miatt - szintén jó lehetőséget biztosítanak a buborékok kialakulására. A keletkező buborékok akkor szakadnak le a pohár felszínéről, amikor már elértek egy kritikus méretet.

Ekkor a rájuk ható felhajtóerő meghaladja a buborék és az üveg között fellépő adhéziós kölcsönhatás nagyságát. Ez nagyon rövid idő alatt bekövetkezik, mivel a felhajtóerő a térfogattal arányosan nő, míg az adhéziós kölcsönhatás a buborék felületével arányos. Ez azt jelenti, hogy az adhéziós erő a buborék sugarának növekedésével lassabban nő, mint a felhajtóerő. Miután a buborék elhagyja keletkezési helyét, ott egy újabb keletkezik, amelyik szintén elérve a kritikus tömeget követi az előző buborékot egészen a felszínig (7. ábra).

A problémafelvetés jól illusztrálja, hogy egy hétköznapi jelenség különböző szinten tárgyalható. A kvalitatív leírás mellett digitális fényképezési eljárással igényes mérések végezhetők. A buborékok gyors mozgása miatt a nagyobb záridejű felvételeken a buborék éles körvonala helyett egy kis csík látható, melynek hossza arányos a buborék pillanatnyi sebességével (8. ábra). Ezek a felvételek ezért alkalmasak arra, hogy másik módszerrel is meghatározzuk a buborékok gyorsulását. Ha a záridő 1/15 s, akkor ez azt jelenti, hogy a buborék 1/15 s alatt az adott csíknak megfelelő, azzal azonos hosszúságú utat tette meg. Így a vonalak hosszának ismeretében, a buborék sebessége számolható.

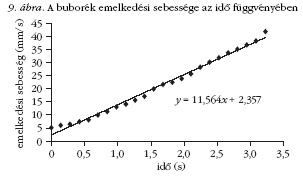
Az iskolán kívüli környezetben, otthon elvégzett mérésekből itt csak egy kiragadott részletet, a buborék mozgásának, felfelé emelkedésének sebességét jellemző grafikont mutatjuk be (9. ábra). (A gyorsulás értéke 11,564 mm/s².)

Konstrukciós feladatok

A konstrukciós feladatok lényege, hogy az adott feladatot a tanulók általában önállóan szerveződő, a feladat jellegéből adódó létszámú csoportokban oldják meg. Az elkészített eszközt, produktumot működés közben, közönség előtt be is mutatják, gyakran verseny keretében, ahol az értékelési szempontok között a kivitel, az esztétikum is szerepet játszik.

Hogyan készítenél galvánelemet gyümölcsbol? Rakjad sorrendbe a gyümölcsöket az általuk létrehozott elektromotoros erő (feszültség) nagysága alapján! (10. ábra)

Készíts vízhajtású autót! Törekedj arra, hogy minél kevesebb "üzemanyaggal" minél nagyobb utat tegyen meg! (11. ábra) Készíts gozhajót, amely a hajótesten képződő vízgőzsegítségével minél messzebbre képes eljutni! (12. ábra) A konstrukciós feladatok különleges szakmai és pedagógiai lehetőséget hordoznak. A merev tanítási óra keretein kívüli, projektszerű tanulói aktivitás, az önálló információgyűjtés (könyvtár-, internethasználat), a csapatmunka, a prezentáció olyan képességek és készségek fejlesztéséhez járul hozzá, amelyek a hagyományos oktatási módszerekkel nem valósulhatnak meg.

Az iskolán kívüli kísérletezés, a konstrukciós feladatok hasznosságáról, sikerességéről, képességfejlesztő hatásáról sok tapasztalatot gyűjthettünk hat év alatt a Szegedi Tudományegyetem Kísérleti Fizikai Tanszéke és az Eötvös Loránd Fizikai Társulat Csongrád Megyei Csoportja által szervezett diákversenyeken. A háromfordulós versenyre általános és középiskolás diákok iskolájuktól függetlenül nevezhetnek be. A verseny eltér a "hagyományos" tanulmányi versenyektől, mert a kitűzött feladatok megoldása nem matematikai számolást, hanem inkább kísérletezést, jelenség értelmezést igényel. A versenynek a Játsszunk Fizikát! nevet adtuk, melyhez minden évben választunk egy híres tudóst, hogy a fizika történetét is népszerűsítsük, és saját kutatómunkára ösztönözzük a diákokat. A verseny célja a diákokban rejlő, a kísérletezés iránti ösztönös vágy felébresztése és ébren tartása, így a kitűzött kísérletek könnyen elvégezhetőek, a tapasztalt jelenségek, pedig többé-kevésbé könnyen megmagyarázhatóak. Nem határozzuk meg szigorúan a szükséges eszközöket és a kísérletek körülményeit, így a diákok tudásuknak megfelelően különböző szinteken, különböző pontossággal végezhetik el a feladatokat [11].

Színielőadások (performance)

A kötetlen, a tanítási órától különböző, színpadi környezetben játszódó tudományos, tudománytörténeti témájú bemutatók a külföldi, de újabban a hazai természettudományos tanítás, tudománynépszerűsítés egyre jobban elterjedő módszere. A színielőadás szereplői általában diákok, de lehetnek tanárok is, a szerzők is változatosak, a "profik" mellett tanár- és diákszerzőkkel is találkozhatunk. Tipikus példája a szórakoztató ismeretterjesztésnek, az előadások gyakran kilépnek az iskolai környezetből, így hatásuk a város, a régió kulturális életében is fontos lehet. A leghasznosabb mégis a színdarabot író, vagy abban szereplő diákoknak, akik játékos formában foglalkoznak természettudománnyal, nagy tudósok élettörténetével. Az alábbi képek (13. ábra) bolgár diákok Aliz kvantumországban, angol tanárok Az ételek fizikája és az országjáró soproni diákok (14. ábra) Douglas Adams: Galaxis útikalauz stoposoknak, avagy az élet, a világmindenség meg minden előadásaiba nyújtanak bepillantást, de a "műfaj" sikeres művelőivel találkozhatunk Debrecenben és Budapesten is.

Értékorzés, hagyományápolás

A természettudomány, így a fizika történetében találkozhatunk olyan felfedezésekkel, amelyek híres tudósok nagy horderejű elveket bizonyító, igazoló kísérleteiként váltak ismertté (pl.: Galilei ejtési kísérletei, Torricelli kísérlete a légnyomás mérésére, Magdeburgi féltekék a légnyomásra és a kölcsönhatás törvényére stb.). Ezek utánépítése és megismétlése laikus érdeklődőket is vonzó esemény, és jó alkalom a tudomány népszerűsítésére. A Föld tengely körüli forgását igazoló, először 1851-ban a párizsi Pantheonban elvégzett Foucault-féle inga kísérletet Magyarországon is több helyen, így a szegedi Dómban - 2006. szeptemberétől a szegedi Szent István téri víztoronyban (15. ábra) is - látványos bemutató keretében reprodukálták.

A projektben részt vevő tanulók az inga elkészítésétől (irodalmazás, tervezés, kivitelezés) a bemutatók anyagának összeállításáig és megtartásáig minden fázisban aktívan közreműködtek (16. ábra). A munka során a tanulók a szakmai haszon mellett többek között a forrásanyag-gyűjtés, a kommunikáció, a prezentáció területén fejlesztették képességeiket, és a sikeres bemutatók során életre szóló, a tudományhoz kapcsolódó élményt szereztek.

Nemzetközi aktivitások

A világháló segítségével ma már számos lehetőség adódik a diákok bevonásával különböző földrajzi helyeken egy jelenség megfigyelésére (pl. napfogyatkozás, Vénusz-átvonulás), vagy egy univerzális mennyiség mérésére (földátmérő mérése, napállandó mérése) egy adott időben. A legfrissebb ilyen jellegű, a diákokat világszerte aktivizáló megmozdulás Einstein halálának 50. évfordulója alkalmából, a 2005 a Fizika Nemzetközi Éve rendezvény keretében meghirdetett "fénystaféta" volt. Nehéz megbecsülni azoknak a tanulóknak a számát, akik a Princetonból 2005. április 18-án induló "fénytovábbításban" részt vettek. A professzionális fényforrások (lézer, katonai reflektorok, autóizzók stb.) mellett az akció sikeréhez szükség volt a diákok zseblámpáira is, akik a felejthetetlen esemény részeseiként iskolán kívül élték át az "einsteini csodákat". A 17. ábra képei a szegedi eseményeket illusztrálják (www.fizikaeve.szeged.hu).

Ahhoz, hogy a fizikaoktatás, a természettudományos nevelés eredményesebb legyen, tudatos "marketing"-tevékenységre van szükség. A "terméket", a használható természettudományos tudást "el kell adni", értékeit bemutatva népszerűsíteni kell nemcsak a diákok körében, iskolán belül a tanárkollégák között, hanem a szülők, az iskolán kívüli szereplők körében, a szűkebb és tágabb nem szakmai társadalmi környezetben is. Az előzőekben bemutatott tanulói aktivitások erre alkalmasak.

A szerzők saját készítésű felvételeik mellett felhasználták Csiszár Imre tanár úr és diákjai, Zátonyi Sándor és Härtlein Károly fotóit. Köszönet érte!

Irodalom

http://www.timss.bc.edu
Vári P., Krolopp J., Egy nemzetközi felmérés főbb eredményei. Új Pedagógiai Szemle 1997. április
Vári P., Gyorsjelentés a PISA 2003 összehasonlító tanulói teljesítménymérés nemzetközi eredményeiről. Új Pedagógiai Szemle 2005. január
B.E. Woolnough, Why students choose physics, or reject it? Physics Education 29 (1994) 368
Csapó B., Az iskolai tudás felszíni rétegei: mit tükröznek az osztályzatok? In: Csapó B. (szerk.) Az iskolai tudás. Osiris Kiadó, Budapest (1998) 39-81
Józsa K., Mi alakítja az énértékelésünket fizikából? Iskolakultúra 9/10 (1999) 72
Papp K., Ami a számszerű eredmények mögött van .... Fizikai Szemle 51/1 (2001) 26
Papp K., Farkas Zs., Virág K., Tóth K., Új időszámítás a természettudományos nevelésben. Fizikai Szemle 53/1 (2003) 20
Radnóti K., A fizika tantárgy helyzete és fejlesztési feladatai egy vizsgálat tükrében. Fizikai Szemle 53/5 (2003) 170
A. Good, Tom Tit második száz legújabb kísérlete. Atheneum, Budapest (1893)
http://titan.physx.u-szeged.hu/opt/physics/expphys/hirek.htm/

Fizikai Szemle honlap

Tartalomjegyzék