Fizikai Szemle honlap

Tartalomjegyzék

Fizikai Szemle 2007/3. 73.o.

A KVANTUM-SZÍNDINAMIKA SZEREPE NAGYENERGIÁJÚ RÉSZECSKEÜTKÖZÉSEK ÉRTELMEZÉSÉBEN

Trócsányi Zoltán
Debreceni Egyetem és MTA Atommagkutató Intézete

Az éleslátás alapja a jó felbontás

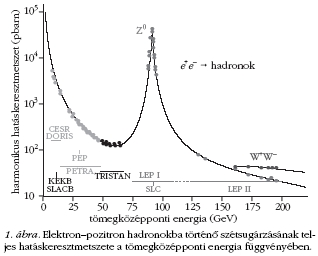
. Minden ember késztetést érez, hogy ismereteket szerezzen a közvetlenül nem észlelt világról, például a természetben előforduló, de szabad szemmel nem látható mintázatokról. Ennek hagyományos eszköze a fénymikroszkóp, amelynek azonban természetes korlátai vannak, és hagyományos fajtáival mikrométernél kisebb méreteket nem lehet feloldani.

A kvantummechanika hőskorának eredménye az a felismerés, hogy a részecskék hullámtermészetet is mutatnak, és minél nagyobb a részecskék energiája, annál rövidebb a hullámhossza. Így elegendően nagy energiára gyorsított részecskékkel a látható fény hullámhosszánál kisebb méretű tárgyak szerkezetét is fel lehet deríteni. Ezen alapszik az elektronmikroszkóp működése, amellyel például a szemünk retinájának nagy felbontású képét is megtekinthetjük. Az elektronok gyorsításának csak a technika szab határt, és a múlt század utolsó harmadának elején már az a merész célkitűzés fogalmazódott meg, hogy nagyenergiájú elektronokkal bombázott protonok szerkezetét a szóródó elektronok szórási képének elemzésével kellene felderíteni. Az ötlet megvalósítóinak Nobel-díjat hozó "SLAC-MIT" kísérletből tudjuk, hogy a protonnak szerkezete van, az elektron a protonban található és jelenleg pontszerűnek ismert alkotórészeken (kvarkokon és gluonokon, összefoglaló néven partonokon) szóródik. Az ilyen mélyen rugalmatlan elektron- proton szórás kicsit felületesen a legnagyobb felbontású mikroszkópnak tekinthető.

Valójában a SLAC-MIT kísérletben nem közvetlenül az elektron, hanem az általa kibocsátott nagy energiájú foton került a partonokkal közvetlen kölcsönhatásba. Már ez is mutatta, hogy a mikroszkóp felbontásának a részecskeenergia növelésével való fokozása szintén természetes korlátba ütközik, ugyanis elegendően nagy energia kis térrészre való sűrítésével új részecskéket lehet előállítani Einstein híres felismerése, a tömeg és az energia egyenértékűsége következtében. Az ilyen folyamatok végállapotainak értelmezése teljesen újszerű megközelítést igényel. A részecskék kölcsönhatásait leíró matematikai modell segítségével a lehetséges végállapotok valószínűségeit tudjuk megjósolni és összevetni a tapasztalattal, ezáltal megerősítve vagy kizárva a modellt. A részecske- kölcsönhatások ma ismert legpontosabb modellje, a Standard Modell, háromféle kölcsönhatást, a gyenge, az elektromágneses és az erős kölcsönhatást írja le. Ez a sorrend egyben a kölcsönhatások erősségének a sorrendje is: a mai kísérleteket jellemző energiákon a harmadik mintegy 15-ször erősebb a másik kettőnél. Ennek megfelelően a részecskék ütközésekor az erős kölcsönhatás által vezérelt folyamatok egy nagyságrenddel gyakoribbak, mint az elektrogyenge folyamatok, és így a kísérletek értelmezésének legfontosabb része az erős kölcsönhatás minél pontosabb leírása.

A Standard Modell anyagi részecskéi a három fermion részecskecsalád tagjai. Egy család két kvarkból és két leptonból (valamint ezek antirészecskéiből) áll. Például a legkönnyebb családba tartozik a protont és neutront felépítő u és d kvark (p = uud, n = udd), az elektron és neutrínója. A másik két család felépítése hasonló, csak az egyes tagok tömege sokkal nagyobb. A fermionok között bozonok közvetítik a kölcsönhatást: a gyengét a nagy tömegű töltött és semleges gyenge bozonok, az elektromágnesest a semleges foton, az erőset az elektromosan szintén semleges, de színtöltéssel rendelkező nyolc gluon.

1. ábra

A korszerű részecskegyorsítók építésének elsősorban az a célja, hogy minél nagyobb energiára gyorsítsuk a részecskéket, és azok ütköztetésével a lehető legnagyobb energiasűrűséget érjük el kis térfogatban, hogy új, a természetben jelenleg nem található részecskéket állítsunk elő és tanulmányozzuk tulajdonságaikat. Az ilyen kísérletek legszebb példái a múlt század utolsó évtizedében működtetett LEP-gyorsító kísérletei. A LEP-gyorsítón elektron-pozitron ütközéseket végeztek eleinte 91,2 GeV tömegközépponti energián, majd nagyobb energiákon, elérve a 209 GeV-et is. A 91,2 GeV arról nevezetes, hogy ez az álló Z0 részecske energiája. Mintegy 17 millió Z0 előállítása révén nagy pontossággal sikerült igazolni a Standard Modell elméleti jóslatait. Például az elektron-pozitron szétsugárzás teljes hatáskeresztmetszetének elméleti jóslata meggyőzően egyezik a különböző kísérletekben mért értékekkel (1. ábra).

2. ábra

A kísérletek egyik központi kérdésköre volt az erős kölcsönhatás elméleti modelljének, a kvantum-színdinamikának (QCD) a kísérleti ellenőrzése. A QCD nem-ábeli, SU(N), mértékelmélet. (Emlékeztetőül: az elektrodinamika ábeli, U(1), mértékelmélet.) Az ilyen elméletek egyik érdekes jóslata, hogy a részecskék közötti kölcsönhatás erősségét szabályozó csatolási paraméter nem állandó. A QCD csatolása annál kisebb, minél nagyobb az ütközésben résztvevő részecskék energiája. Ennek az aszimptotikus szabadságnak nevezett jelenségnek 1973-ban történt felismeréséért kapta Gross, Wilczek és Politzer a 2004. évi fizikai Nobel-díjat. Azért éppen 2004-ben, mert a jelenség kísérleti igazolására akkorra gyűlt össze elegendően meggyőző kísérleti tapasztalat (2. ábra).

Az aszimptotikus szabadságlehetővé teszi, hogy perturbatív leírásmódot használjunk, amelyben a kölcsönhatást a csatolás szerinti sorfejtés segítségével vesszük figyelembe. A perturbációszámítás része az egyetemi bevezető kvantummechanika tananyagnak, és aki azt jól megtanulta úgy gondolhatja, hogy ez egy jól megértett, "lezárt" témakör. Nos a QCD esetében ez távolról sincs így. Hogy miért nem, a nagyenergiájú elektron-pozitron ütközések példáján mutatom be.

3. ábra

A Z0 részecske tömegének megfelelő tömegközépponti energián működő LEP-en az elektron és pozitron ütközése során nagy valószínűséggel Z0 keletkezik. Hamar elbomlik, fermionpár keletkezik belőle, az esetek 60%-ában kvark-antikvark pár. A kvarkok egymáshoz nagyon közel, nagy energiával keletkeznek, és így aszimptotikusan szabadon mozognak - használható a folyamat leírására a perturbatív QCD. Igaz ugyan, hogy az egymástól távolodó kvarkok között egyre nagyobb "szín"-erő hat, és az így felhalmozódó térenergia ahhoz vezet, hogy új részecskék keletkeznek, az észlelő-berendezésekben már nem az eredeti két kvarkot látjuk, hanem részecskék záporát (hadronzáport). A folyamat azonban emlékét őrzi a kezdeti két kvark által szállított lendületnek és perturbációszámítással meglehet jósolni a két hadronzáport tartalmazó események valószínűségét. Találtak három hadronzáport tartalmazó eseményeket is, amelyeket úgy lehet értelmezni, hogy a kezdeti két kvarkkal együtt egy gluon is keletkezett (3. ábra ).

4. ábra

A QCD-ben a perturbatív leírás első bonyodalma éppen a csatolás változása. Ha a végállapotokat nem osztályozzuk a hadronzáporok száma szerint, csupán leszámoljuk a hadronikus végállapotokat, akkor a teljes hadronikus hatáskeresztmetszetet mérhetjük meg. A perturbációszámítással kiszámított teljes hatáskeresztmetszet tükrözi a csatolás változását, a jóslat függ attól, mekkora energián vesszük a csatolást. Igen ám, csakhogy ez az energia nem mérhető, ezért a jóslatunk nem használható jóslat. A nemfizikai paramétertől való függést nevezzük renormálási skálafüggésnek. Szerencsére a perturbációszámítás egy másik tulajdonsága segítségünkre siet. Belátható, hogy a perturbációszámítás egyes rendjeiben a µ renormálási skálától való függés eggyel mindig magasabb rendű, mint a számítás adott rendje. 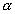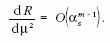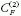Például, ha az R fizikai mennyiséget a perturbáció nagyságát jellemző képlets csatolás m-edik rendjében számítjuk ki, akkor a skálafüggés nagyságrendje m+1-ed rendű:

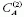képlet

Így minél tovább megyünk a perturbációs sor kiszámításában, annál kisebb a skálafüggés (4. ábra). A QCD-ben tehát elengedhetetlen a sugárzási korrekciók figyelembevétele, ha mennyiségileg értelmes jóslatot akarunk tenni.

A második bonyodalommal a sugárzási korrekciók számításakor találkozunk. A Lagrange-sűrűségből meghatározott szabályok szerint ki lehet számítani a mátrixelemeket, a hatáskeresztmetszet pedig a mátrixelemek négyzetével arányos. Born-közelítésben a teljesen differenciális hatáskeresztmetszetnek a fázistér feletti integrálja véges. A mátrixelem négyzetéhez kétfajta elsőrendű korrekciót találunk. Az egyik esetben egy valódi részecske jelenik meg a végállapotban, a másikban egy virtuális részecskefluktuáció történik (hurokkorrekció). Mindkét járulék önmagában végtelen, azonban az összegük véges, ha infravörös véges fizikai mennyiség hatáskeresztmetszetét jósoljuk. Az infravörös végesség minőségileg azt jelenti, hogy egy feloldatlan, nem megfigyelhető részecske megjelenése a végállapotban nem változtatja meg a mennyiségértékét. Például a hadronzáporok száma attól nem változik, ha az egyik végállapoti részecske egy párhuzamosan tovarepülő részecskepárra bomlik, vagy keletkezik egy lágy (nagyon kicsi energiájú) részecske. Így, ha meghatározott számú hadronzápor keletkezésének hatáskeresztmetszetét számítjuk, akkor a valós és virtuális korrekció összege véges. A véges eredményt azonban nem könnyű megkapni, ugyanis a kétféle járulékot más fázistér felett kell integrálni, ezért az összegzés az integrandus szintjén nem lehetséges.

Ma már az irodalomban léteznek általános eljárások arra, hogyan lehet folyamattól és fizikai mennyiségtől függetlenül a számításokat úgy szervezni, hogy a véges korrekciót megkapjuk, és ismerjük számos alapvető folyamat esetén a QCD sugárzási korrekciót. Ezek egyik szép példája az elektron-pozitron hadronokba történő szétsugárzásában négy hadronzápor keletkezése, amely a QCD LEP-en történő pontos ellenőrzésének lehetőségét nyújtja. A négy hadronzáporos végállapotok ugyanis számszerűleg a csatolás nagyságától, geometriai szerkezetüket tekintve pedig a QCD színtöltéseitől is függenek. A színtöltések a mértékcsoportot meghatározó algebra kvadratikus Casimir-operátorának értékei az alap és adjungált ábrázolásban. (A perdület operátoralgebrája SU(2), amelynek kvadratikus Casimirja a perdület négyzete, J2. Ennek sajátértéke C(2) = j(j+1). 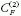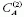Alapábrázolásban j = 1/2, ezért képlet = 3/4, adjungált ábrázolásban képlet = 2. A megfelelő értékek QCD-ben (SU(3)) képlet = 4/3, képlet = 3.) Így a hadronzáporok gyakorisága és térbeli elhelyezkedésének mennyiségi jellemzése alapján a csatolás és a színtöltések egyszerre mérhetőek. Ilyen méréseket a LEP együttműködéseiben többször is végeztek. Az eredmények összefoglalását találjuk a 5. ábrán. A mérések nagyon pontosan megerősítik a QCD-értékeket.

5. ábra

A LEP kísérleti eredményeit a Standard Modellel nagy pontossággal lehet leírni. Mégsem mondhatjuk, hogy sikerült a LEP-en a Standard Modellt egyértelműen igazolni. A Standard Modell ugyanis olyan lokális mértékelméletre alapul, amelyet a Lagrange-sűrűségben szereplő, a terek négyzetével arányos tömegtagok sértenének, ezért azok a kiindulási elméletben nem szerepelnek (például a QCD Lagrange-sűrűségében sem). Ugyanakkor tapasztalatból tudjuk, hogy a részecskéknek van tömegük, amiről az elméletnek számot kell adni. A Standard Modellben ez a Higgs-mechanizmus eredménye, aminek lényege, hogy az elemi részecskék egy egyelőre csak feltételezett skalártérrel, a Higgs-térrel való kölcsönhatás eredményeként nyerik tömegüket. (Az összetett részecskék, mint például az anyagot felépítő proton és neutron, tömegének túlnyomó részéért a QCD felelős - egyelőre nem tudjuk milyen módon.) Ha a Higgs-tér létezik, akkor elő lehet állítani elemi gerjesztését, a nulla spinű Higgs-részecskét, ha elegendő energiasűrűséget sikerül előállítani a laboratóriumban. A LEP kísérletei Higgs-részecskét nem találtak (bár "gyanús" eseményekre akadtak).

6. ábra

A jelenleg épülő LHC-gyorsító elsődleges célja a Higgs-részecske laboratóriumi előállítása. Protonok fognak ütközni 14 TeV tömegközépponti energián. Ahogy említettem a protonok összetett részecskék, nagyenergiájú ütközéseik során az elemi kölcsönhatás a bennük található kvarkok és gluonok között játszódik le. Ahhoz, hogy ezeket az eseményeket egyáltalán értelmezni lehessen szintén a QCD-re van szükség. A QCD-ben a nagyenergiájú részecskeütközések leírásának leglényegesebb eszköze a faktorizációs tétel (6. ábra). Eszerint a protonban található partonok közül egy vesz részt az elemi kölcsönhatásban, amelynek hatáskeresztmetszetét a perturbatív QCD szabályai szerint számolhatjuk. A parton a proton (négyes)lendületének egy bizonyos hányadát viszi az ütközésbe, amelyet a partonsűrűség-függvény ad meg. A partonsűrűség- függvény perturbatív módon ugyan nem számolható, azonban folyamattól független, ezért egy folyamatban megmérve más folyamatban már használható a fizikai hatáskeresztmetszet kiszámításához. Az egyes szórási kísérletek persze különböző energián történhetnek, ezért szükség van az fi partonsűrűség- függvény energiafüggésének ismeretére is, ami azonban perturbatív módon ismét csak megadható fi és a Pij Altarelli-Parisi-függvények konvolúciójaként,

képlet

(Az Altarelli-Parisi-függvények írják le az elemi partonbomlás valószínűségét.) A partonsűrűség-függvény pontos mérése megköveteli, hogy a méréshez használt szórási folyamat elemi hatáskeresztmetszetét pontosan ismerjük, amihez elengedhetetlen a sugárzási korrekciók ismerete az adott folyamathoz.

A 7. ábra szerint a LEP-kísérlet eredményeinek kiértékelése azt mutatja, hogy a Higgs-részecske tömege nagy valószínűséggel 100-200 GeV/c2 közé esik (amennyiben létezik). Az LHC-n történő ütközésekben ekkora energiájú részecskét könnyedén elő lehet majd állítani. Az észleléshez azonban nem elegendő az előállítás. A Higgs-részecske ugyanis rövid élettartamú, előszeretettel nehéz részecskékbe bomlik, adott részecskével való kölcsönhatásának erőssége ugyanis a részecske tömegével arányos (8. ábra). A keletkező egyéb, Standard Modellbeli nehéz részecskék szintén tovább bomlanak elsősorban az erős kölcsönhatás révén, így a végállapotok többsége ugyanúgy sok hadront tartalmaz, mint egy egyszerű QCD-esemény, amelyben nem keletkezett Higgs-részecske, tehát e jel nem válik ki a háttérből. A LEP által legvalószínűbbnek tartott Higgs-tömeg esetén érdekes módon a két fotonba való bomlás vezet olyan végállapothoz, ahol a jel/háttér hányados a legkedvezőbb a felfedezéshez.

7. ábra

A kétfoton spektrumban a Higgs-rezonancia jól látható (9. ábra), felfedezése nem okoz elvi gondot, "csupán" kemény kísérleti munkát igényel. Azonban egyáltalán nem bizonyos, hogy a felfedezett rezonancia a Standard Modell Higgs-részecskéjét jelzi. A standard Higgs esetében a QCD-korrekciók jelentősen befolyásolják a csúcs magasságára vonatkozó elméleti jóslatot. A Higgs-jel kétfotonos csatornája esetén például az első sugárzási korrekció kétszeresére növeli a vezető rendben számolt hozamot, míg az arra következő (második) korrekció további 15%-os növekedést jelent. Ugyanígy az elképzelések a Standard Modellen túli fizikáról, például a szuperszimmetrikus részecskék létezése, nagyban befolyásolhatja a csúcs magasságát. Egy csúcs észlelése tehát önmagában kevés, szükséges a lehetséges elméleti értelmezéseket olyan pontosan megadni, hogy a mért jellemzők alapján ki lehessen választani azt a modellt, amely összeegyeztethető a méréssel.

8. ábra

A felfedezés első öröme után pedig rögtön jön az új részecske tulajdonságainak meghatározása. Ezek a kísérleti analízisek akkor sikeresek, ha pontosak. A mérések pontos kiértékelése akkor lehetséges, ha minél pontosabban ismerjük

9. ábra

Mindezek a jelenlegi ismereteinknél pontosabb elméleti leírást igényelnek, bizonyos folyamatok esetén nagy szükség lenne a második sugárzási korrekciók ismeretére. Az elmúlt évtizedben jelentős erőfeszítések árán fontos eredmények jelentek meg az irodalomban egy olyan általános eljárás kidolgozása végett, amellyel folyamattól és fizikai mennyiségtől függetlenül a véges másodrendű korrekciót megkapjuk, azonban még további nehéz feladatok várnak megoldásra.

A QCD csodálatos elmélet. Hitünk szerint a fél oldalon leírható Lagrange-függvénye minden lehetséges ismeretet tartalmaz az elemi részek erős kölcsönhatásának fizikájáról. Eddigi tapasztalatunk ezt a hitet megerősíti. A tömör Lagrange-függvény rendkívül gazdag szerkezettel rendelkező elméletet takar. Már több mint 30 éve kutatók százai foglalkoznak az elméletből kibontható, a kísérletekkel összevethető jóslatok kikutatásával, aminek egyik legfontosabb eszköze a perturbatív térelmélet. Leginkább a szobrászathoz tudnánk e tevékenységet hasonlítani. Ahogy egy szép darab márványban a szobrász meglátja a belőle kifaragható, szemet gyönyörködtető szobrot, úgy próbáljuk a QCD Lagrange-függvényében rejlő gyönyörű matematikai összefüggéseket kibontani. A cél azonban nem elsősorban szép képletek gyártása, a "faragás" sikerét nem csupán az esztétikum dönti el. A sugárzási korrekciók számszerű meghatározása az elemi részecskék szórási folyamataiban a kísérletekkel való egyre pontosabb összehasonlítás, tehát az éleslátás elengedhetetlen eszköze.