Fizikai Szemle 2007/7. 217.o.
LEJTŐN LEFOLYÓ SZEMCSÉS ANYAG DINAMIKÁJA:
INSTABILITÁSOK, LAVINÁK
Börzsönyi Tamás
MTA Szilárdtestfizikai és Optikai Kutatóintézete
Szemcsés anyagokkal a mindennapi életünkben, az
iparban és a természetben is gyakran találkozunk
[1-3]. Ennek ellenére viselkedésüket sok esetben
mind a mai napig megjósolhatatlannak találjuk. Gondolhatunk
a hegyoldalakon megfigyelhető, előre nem
jelezhető kőlavinákra, vagy a nagy mechanikai feszültség
hatására összedőlő gabonasilókra. Gyakran
gondot okoz az ipari folyamatok tervezőinek, hogy a
szemcsés anyag "nem normálisan" viselkedik, például
különböző méretű szemcsék összekeverésénél az
anyag a keverés, vagy rázás hatására inkább szétválik,
vagy más esetben csöveket dugít el, ahol pedig a számítások
szerint folynia kellene. Így a szemcsés anyagok
mechanikai, dinamikai tulajdonságainak vizsgálata
ma is aktív kutatási terület, ami sok más területtel
is összefügg. Erre egy jó példa a közlekedésdinamika,
ahol az autók vagy gyalogosok mozgását leíró modellek
gyakran szoros rokonságot mutatnak a szemcsés
anyagok áramlási modelljeivel.
A szemcsés anyagok dinamikai viselkedését érdekes
dualitás jellemzi. Egyfelől, a dobozból elég gyorsan
kiöntött cukor, vagy kávé a folyadékokhoz nagyon
hasonlóan folyik, másrészt, a folyás megindulásának
vagy - lassú öntés esetén megfigyelhető - szakaszosságának
legegyszerűbb leírásához abból érdemes kiindulni,
hogy az anyag nagyon sok, piciny szilárd egységből
áll. A szemcsés anyagokkal foglalkozó kutatókat,
mérnököket régóta foglalkoztatja, hogy milyen
módon lehetne a szemcsés anyagok dinamikai jelenségeit
a folyadékdinamikai kontinuum-egyenletekhez
hasonló keretek között tárgyalni. Az egyik nehézség,
hogy a szemcsés anyag - ellentétben a normál folyadékokkal-
összenyomható, és sűrűsége nagyon tág határok
között változhat. Egy dobozban lévő anyagot intenzíven
rázva könnyen elérhető a nagyon ritka gázszerű
fázis, a doboz mozgatását fokozatosan lassítva pedig a
mozgásban lévő anyag sűrűsége folyamatosan növekszik,
megközelítve a nyugalmi sűrűséget. Egy másik
nehézség, hogy, ellentétben az átlátszó folyadékokkal,
amelyekben az áramlási teret az anyag belsejében is
viszonylag könnyen feltérképezhetjük a folyadékba
helyezett "tracer" részecskék mozgását követve, a
szemcsés anyagok áramlását legtöbbször csak a felületen
tudjuk nyomon követni. Így jóval kevesebb információból
kell rekonstruálnunk, hogy milyenek is lehetnek
a különböző geometriákban megfigyelhető áramlási
terek, illetve az azokat meghatározó törvényszerűségek.
A manapság már viszonylag elérhető árú, gyors
videokamerák (néhány ezer kép/másodperc) elterjedésével egyre
intenzívebb adatgyűjtés folyik, hogy a
szóba jöhető modelleket teszteljük. A különböző nyírási
geometriák mellett az egyik gyakran vizsgált eset -
egyszerűsége miatt is - az érdes felületű lejtőn lefolyó,
nem túl vastag szemcsés réteg.
A folyadékok mozgásának leírásánál a nyírófeszültség
és a nyírás következtében létrejövő sebességgradiens
között lineáris összefüggést találunk, amit egy
lényeges anyagi paraméter, a viszkozitás jellemez.
Egyszerű (newtoni) folyadékok esetében ez a viszkozitás
konstans, bonyolultabb esetekben (pl. polimeroldatoknál)
függ a nyírás erősségétől. A szemcsés
anyagok esete még ennél is bonyolultabb, mivel itt
hagyományos értelemben vett viszkozitásról sem beszélhetünk,
hiszen a nyírófeszültség általában nem a
sebességgradiens első hatványával arányos. Ha a lejtőn
lefolyó anyag esetét nézzük, akkor newtoni folyadékoknál a
felszíni sebesség a rétegvastagság négyzetével arányosan
nő, ami a konstans viszkozitás következménye.
Egy angol mérnök - R.A. Bagnold - a második
világháború utáni években intenzíven érdeklődött,
hogy hogyan is lehet ez a szemcsés anyagok
esetében. Azzal a modellel állt elő, hogy itt a nyírófeszültségnek
a sebességgradiens második hatványával
kell arányosnak lennie. Érvelése szerint a lejtővel
párhuzamos, egymás fölötti rétegekben lévő, egymással
ütköző részecskék közötti lendületátadás a sebességgradiens
mértékével arányos. Másrészt, ezen ütközések
frekvenciája szintén lineárisan függ a sebességgradienstől.
Az így megindokolt négyzetes összefüggés
ahhoz vezet, hogy a felszíni sebesség nem a vastagság
négyzetével, hanem annak csak 3/2-ik hatványával növekszik.
Ez az, amit egyszerű kísérletekkel
igazolni lehet, és az elmúlt néhány évben többen is
kimutatták, hogy valóban így van, de csak addig,
amíg az anyag viszonylag lassan áramlik és sűrűsége
nagy, azaz alig tér el a nyugalmi sűrűségtől. A nagyon
lassú határesetben a Bagnold-modell ismét érvényét
veszti, ezt az úgynevezett kvázisztatikus nyírási tartományt
más geometriában intenzíven vizsgálják [4].
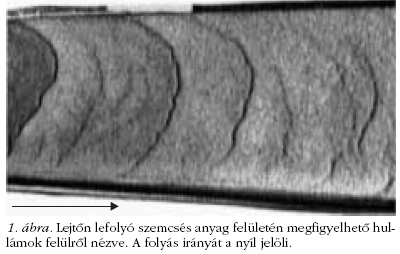
A lejtőn lefolyó réteg vizsgálata azonban nem csak a
fenti alaptulajdonságok szempontjából érdekes, hanem
azért is, mert a homogén állapot gyakran instabillá válik
és különféle mintázatok alakulhatnak ki. Ezek lehetnek
hasonlóak azokhoz, amilyeneket a hagyományos
folyadékoknál is láthatunk, de vannak olyanok is, amelyeket
folyadékokban eddig nem figyeltek meg.
A lejtő meredekségét növelve, a folyás megindulása
után a homogén állapot első instabilitása hullámok kialakulásához
vezet (lásd 1. ábra). Az már régóta ismert
tény, hogy egy függőleges falon vagy lejtőn lefolyó vékony
folyadékréteg instabillá válik és hullámok alakulnak
ki. A jelenséget Kapitza-instabilitásként szokták emlegetni.
Az utóbbi években ezt az instabilitást többen is
vizsgálták szemcsés anyagokra, és azt tapasztalták, hogy
ugyan az instabilitás a folyadékokban megfigyelthez hasonlóan
inerciális eredetű, a hullámok tulajdonságai mégis
lényegesen eltérőek [5]. Ezeknél az anyagoknál
ugyanis - a newtoni folyadékokkal ellentétben - az instabilitási
küszöb könnyen eshet a folyási határ alá,
vagyis az instabilitás rögtön az áramlás megindulásánál
jelen lesz. Ez annak a következménye, hogy a lejtőre
helyezett szemcsés anyag csak egy kritikus hc vastagság
fölött kezd el folyni, illetve egy ennél kicsit kisebb hs
vastagságnál a folyás megáll. Így a szemcsés anyagot
vizsgálva azt tapasztaljuk, hogy a hullámok rögtön a folyás
megindulása után kialakulnak. A vastagabb részeknél
az áramlás felgyorsul, míg máshol elvékonyodik, lelassul
és meg is áll. Ily módon a lejtő aljára az anyag már
diszkrét csomagokban (lavinákban) érkezik.
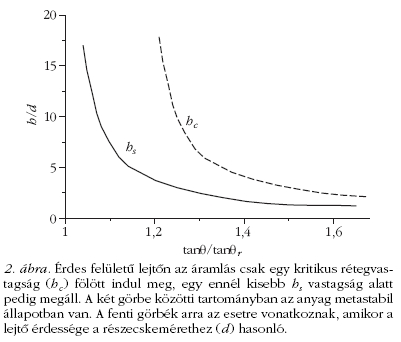
A két mennyiség - hs és hc - fontos paraméter és a
2. ábrán látható módon függ a lejtő dőlésszögétől. A
két görbe végtelenbe fut a lejtő meredekségének egy
meghatározott értékénél. Azt a szöget, ami egy föntről
növesztett homokdomb oldalán alakul ki azután,
hogy abbamarad a bejövő anyagáram és a még mozgásban
lévő szemcsék mind lefolynak, rézsuszögnek
(θr ) nevezzük, és, mint az várható, ez a hs görbe
aszimptotája (2. ábra). Ez a szög körülbelül 31° homokszemcsék
esetén és 21° üveggolyók esetén.
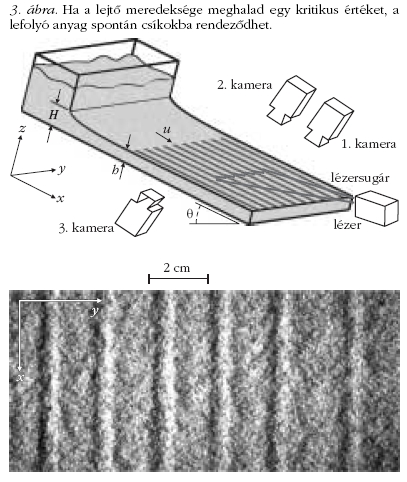
A lejtő meredekségét növelve, az áramlás gyorsulásával
egy másik, talán még érdekesebb instabilitás figyelhető
meg, amelynek során az anyag a 3. ábrán látható
módon csíkokba rendeződik. Ez a jelenség hagyományos
folyadékokban hasonló körülmények között nem
figyelhető meg. Érdekes, hogy ez egy csak nem régen
felfedezett jelenség annak ellenére, hogy viszonylag tág
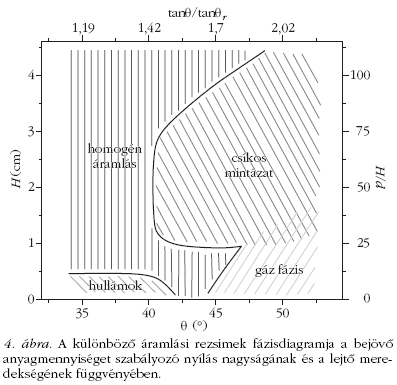
tartományban megfigyelhető. Ha a fázisdiagramot szemléljük
(4. ábra), amelyen a bejövő anyagmennyiséget
szabályozó nyílás H nagysága és a lejtő meredeksége
függvényében ábrázoltuk a különböző áramlási rezsimekhez
tartozó tartományokat, akkor láthatjuk, hogy
egy jó nagy részt a csíkokból álló mintázat foglal el, míg
például az előzőekben ismertetett hullámok csak a fázisdiagram
kis szegletéhez tartozó paramétereknél (vékony,
lassú rétegnél) figyelhetők meg. Látható továbbá
az is, hogy csíkok csak egy kritikus lejtőmeredekség fölött
figyelhetők meg. A küszöbmeredekség sok általunk
vizsgált, különböző rézsűszöget formáló anyagra univerzálisan
a tanθ/tanθr ≈ 1,4 értéknek felel meg.
Vizsgáljuk meg most a csíkokból álló mintázat szerkezetét
és kialakulásának körülményeit. A 3. ábrán látható
lézernyaláb felületről visszavert fényét az 1. kamera
segítségével detektálva meghatározhatjuk, hogy a
mintázathoz milyen magasságmoduláció tartozik. A
másik két kamera segítségével a sebességteret határozhatjuk
meg az áramló réteg felszínén, illetve a legalsó
rétegnél közvetlenül a lejtő fölött (egy erre a célra készített
ablakon keresztül). Az első dolog, amit elemezni
érdemes az, hogy a mintázat a lejtő meredekségét változtatva
széles tartományban megfigyelhető, viszont tulajdonságai
a lejtő meredekségének növelésével drasztikusan
változnak. Ennek feltérképezésére készítettünk
egy olyan rendszert, amely az összes kiegészítő berendezéssel
együtt (kamerák, lézer stb.) könnyen billenthető.
Ennek segítségével nemcsak a különböző rezsimeket
határoztuk meg, hanem módunk nyílt azt is
megmérni, hogy hogyan változik az áramló anyag átlagos
sűrűsége a lejtő meredekségének növelésével [6].
Ezt úgy tettük, hogy a fent említett módszerrel detektáltuk
az áramlási vastagságot, miközben a lejtőt hirtelen
visszabillentettük, és az áramlást befagyasztottuk. A
mérést kellő körültekintéssel végezve könnyen meghatározhatjuk
az áramlási és a nyugalmi sűrűség hányadosát.
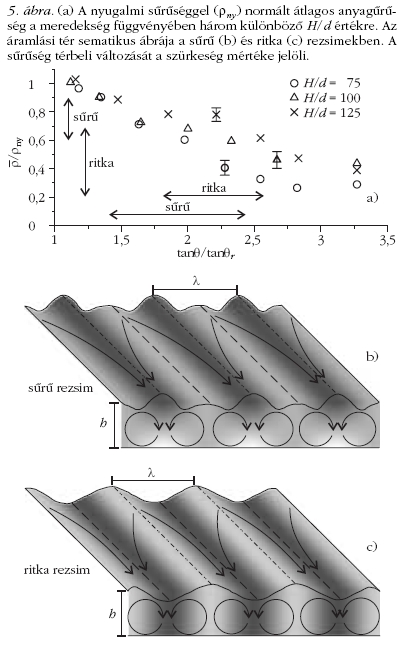
Az 5. ábrán látható, hogy ez a hányados erőteljesen
csökken a lejtő meredekségének növelésével. Azt
is láthatjuk, hogy két különböző szerkezetű mintázatot
találtunk, amit sűrű és ritka rezsimként jelöltünk, mivel
az egyikhez tartozó átlagos sűrűség a 0,6ρny -0,9ρny a
másikhoz tartozó pedig a 0,2ρny -0,7ρny tartományban
van. A két rezsim közös vonása, hogy az áramlási vastagság
periodikusan változik az y irányban, viszont
lényeges különbség, hogy míg a ritka rezsimben a vastagságminimumokhoz
sebességmaximum tartozik, addig
a sűrű rezsimben épp fordítva, azaz az áramlási
sebesség a vastagságmaximumnál a legnagyobb. A felszínen
mért áramlási térkép arra enged következtetni,
hogy az áramlási tér vortex jellegű, ahogy azt az 5.b-c
ábrákon vázoltuk. Ez lehet annak a következménye,
hogy az instabilitás bizonyos tekintetben hasonlít a
folyadékok esetében jól ismert Rayleigh-Benard-instabilitáshoz,
amikor is egy alulról fűtött folyadékrétegben
hengeres áramlás alakul ki, mivel a melegítés hatására
a folyadék alsó része kicsit kitágul, és a fölötte lévő
hidegebb (sűrűbb) folyadékréteggel instabil konfigurációt
alkot. Ilyen úgynevezett sűrűséginverzió jöhet létre
a szemcsékből álló rétegben is, ahol az érdes felületű
lejtővel való ütközések hatására a részecskék közötti
átlagos távolság kicsit megnő a lejtőhöz közelebbi részen,
vagyis egy viszonylag sűrűbb réteg csúszik egy
ritkább réteg tetején [7]. Az, hogy az instabilitás emiatt
jön-e létre, vagy pedig a hengeres konvekció már egy
másodlagos következmény, még nem tisztázott. Úgy
tűnik ugyanis, hogy a mintázat kialakulása gyorsuló folyásnál
történik, és, amikor a folyás a lejtőn lefelé haladva
eléri a végsebességét (már nem gyorsul tovább),
a mintázat elhalni látszik. Így a folyás gyorsuló mivolta
is fontos tényezőnek tűnik a mintázat kialakulása szempontjából.
Mint már korábban említettük, kevés bejövő anyagmennyiség
esetén az áramlás szakaszossá válik. Ennek
egy extrém határesete, amikor olyan kis ütemben
szórjuk a lejtő tetejére a szemcséket, hogy csak nagyritkán
indul meg egy-egy lavina. Ezek a lavinák aztán
formájukat és sebességüket tartva stacionárius módon
haladnak lefelé a lejtőn lévő sztatikus réteg felszínén.
A lavinák tulajdonságait vizsgálva azt tapasztaltuk,
hogy nagy mértékben függenek a szemcsés anyag
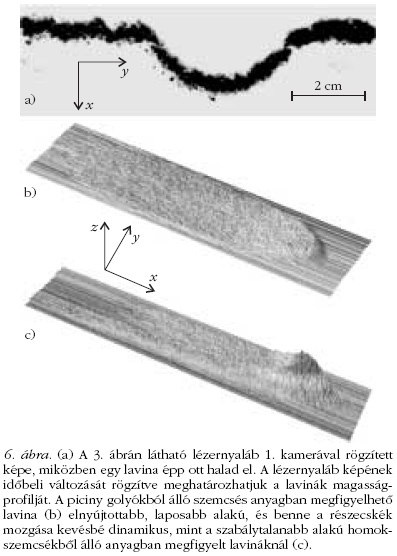
milyenségétől [8]. Elsőként vegyük szemügyre a lavinák
alakját. A 6.a ábrán láthatjuk a 3. ábrán látható
lézernyaláb 1. kamerával rögzített képét. Ahogy a
lavina elhalad, a lézernyalábról felvett kép az időben
változik, amiből rekonstruálhatjuk a lavina magasságprofilját
(6.b-c ábrák). Piciny golyókat használva a
lavinák alakja elnyújtottabb, és magasságuk csak ritkán
haladja meg a 2hs értéket (6.b ábra). Ezzel szemben
a kicsit szabálytalanabb alakú, de még mindig
nem túl sarkos homokszemcsékből álló anyag esetében
a lavinának egy magas, dinamikus frontja van,
amelynek magassága 3hs-4hs (6.c ábra).
A nagy sebességű kamerával felvett felvételeken [9]
látható, hogy az említett két esetben megfigyelhető
lavináknak nem csak az alakja gyökeresen különböző.
A szabálytalanabb homokszemcsék esetén a lavinafrontból
kirepülnek a részecskék, azaz a tipikus
részecskesebesség (kb. 30%-kal) nagyobb, mint a lavina
haladási sebessége. Golyókból álló rendszer esetében
viszont a lavina haladási sebessége nagyobb -
mintegy másfélszerese - a legnagyobb részecskesebességnek.
Itt ugyanis a lavina haladása úgy történik,
hogy a lejtőn nyugalomban lévő (hs vastagságú) rétegben
lévő részecskék mozgásba jönnek a kicsit fentebb
lévő, már mozgó részecskékkel meglévő kontaktusaik
folytán.
A fentiekben ismertetett és az azokhoz hasonló
egyszerű kísérletekkel fontos információkat tudhatunk
meg a szemcsés anyagok alaptulajdonságairól,
segítségükkel megérthetünk a természetben megfigyelt
vagy ipari folyamatokban lejátszódó jelenségeket.
Egy igen erős motiváció azonban a numerikus
modellek érvényességi körének tesztelése is. A számítógépes
modellezésben az eszközrendszer folyamatos
fejlődésével a valóságot egyre pontosabban leíró
rendszereket tudunk vizsgálni, ily módon költséges
kísérletek elvégzése helyett szimulációk segítségével
jósolhatunk meg fontos jelenségeket. A modellekben
számos egyszerűsítéssel szokás élni, amelyek jelentősen
javítják a numerikus számolások hatékonyságát,
viszont bizonyos mértékig korlátozzák is azok érvényességi
körét. Egyik ilyen egyszerűsítés, hogy az
esetek túlnyomó többségében gömb alakú szemcséket
használnak. Sok példát találhatunk arra, hogy
kísérletet piciny gömbökkel és szabálytalan alakú
homokszemcsékkel elvégezve hasonló viselkedést tapasztalunk,
ilyen volt például a csíkokból álló mintázat,
de könnyen találhatunk lényegesen eltérő viselkedést
is. Ilyen például a hullámok esete, ahol a két
esetben kvalitatívan hasonló, de kvantitatívan nagyon
különböző dinamikát találunk, vagy a lavinák, ahol a
két rendszer viselkedése nemcsak kvantitatívan, hanem
már kvalitatívan is eltérő.
Irodalom
- Vankó P., Izgalmas mérések a mérnök-fizikus hallgatói laboratóriumban.
Fizikai Szemle 56 (2006) 307
- Jánosi I., A homok titkai. Természet Világa 129 (1998) 19
- Jánosi I., Zajongó homokdombok és egyéb furcsaságok: új fejlemények
a granuláris anyagok fizikájában. Fizikai Szemle 45
(1995) 78
- Unger T., Török J., Kertész J., Wolf D.E., Shear band formation
in granular media as a variational problem. Physical Review Letters
92 (2004) 214301
- Forterre Y., Pouliquen O., Long-surface-wave instability in
dense granular flows. Journal of Fluid Mechanics 486 (2003) 21
- Börzsönyi T., Ecke R.E., Rapid granular flows on a rough incline:
phase diagram, gas transition, and effects of air drag.
Physical Review E 74 (2006) 061301
- Forterre Y., Pouliquen O., Longitudinal vortices in granular
flows. Physical Review Letters 86 (2001) 5886
- Börzsönyi T., Ecke R.E., Two scenarios for avalanche dynamics
in inclined granular layers. Physical Review Letters 94 (2005)
208001
- Nagy sebességű kamerával készült videofelvételek és további
információk elérhetők a http://www.szfki.hu/~btamas/gran/gran.html
internetes oldalon.
__________________________
A vizsgálatokat az OTKA-F-060157 kutatási pályázat támogatásával
és az MTA Bolyai János Kutatási ösztöndíj segítségével végeztem.
